基础算法篇(5)(蓝桥杯常考点)—动态规划(C/C++)
文章目录
- 动态规划
- 前言
- 线性dp
- 路径类dp
- 经典线性dp
- 背包问题分类
- 01背包问题
- 完全背包问题
- 多重背包
- 分组背包问题
- 混合背包问题
- 多维费用的背包问题
- 区间dp
动态规划
前言
在竞赛中,如果遇到动态规划的题目,只要不是经典题型,那么大概率就是以压轴题的形式出现
用动态规划解决问题的步骤:(递推形式)
1.定义状态表示:
根据经验+需要的意义,赋予dp数组相应的含义
(主要还是看需要记什么)
2.推导状态转移方程:
在dp表中分析,当前格子如何通过其余格子推导出来的
3.初始化:
将显而易见的以及边界情况下的位置填上值,来让后续填表的结果是正确的
4.确定填表顺序:
根据状态转移方程,确定按照什么顺序来填表
5.找出最终结果:
在表中找出需要的最终结果
洛谷 P10250 [GESP样题 六级] 下楼梯
洛谷 P1216 [USACO1.5] [IOI1994]数字三⻆形 Number Triangles
动态规划常要空间优化:
即把不用了的值给不要了
但是背包问题如果不能用1个数组优化,而要多个数组的话,那就不空间优化了,否则可能会超时
常见的优化方法:
方法一:一维转几个数
例题:洛谷 P10250 [GESP样题 六级] 下楼梯方法二:二维转一维
1.是否需要修改遍历顺序
2.删掉一维即可
例题:洛谷 P1216 [USACO1.5] [IOI1994]数字三⻆形 Number Triangles
洛谷 P1115 最⼤⼦段和
洛谷 P1541 [NOIP2010 提⾼组] 乌⻳棋
一些技巧:
1.状态表示:
a.研究子数组或子序列问题时,从某个位置结尾来定义状态表示 例:洛谷 P1115 最⼤⼦段和
b.优化问题:有一维可以由其他维的数据推出的话,可以不要这一维(不是指那个空间优化方法)例题:洛谷 P1541 [NOIP2010 提⾼组] 乌⻳棋2.状态转移方程:
a.求方案数一般是相加
b.常从最后一步开始分析去推导状态转移方程3.初始化:
在求方案数时,一般将第一个位置初始化为1,其他位置为0
线性dp
特点:状态转移只依赖于前一个或前几个状态;状态之间的关系是线性的
路径类dp
洛谷 P1004 [NOIP2000 提⾼组] ⽅格取数
走两次的得到的值之和最大问题:
(两次的规则要一样,走到不同位置的得到的值不一样,且每位置的值只能得一次)
例题:洛谷 P1004 [NOIP2000 提⾼组] ⽅格取数
在状态表示时:两者如果是同时出发的(非同步则要改一点),其横纵坐标之和会是一个定值
一般表示为f[st][i1][i2]:
意思是:第一条路在[i1,st-i1],第二条路在[i2,st-i2]时,两者的路径(取数)之和最大
经典线性dp
经典线性dp问题有两个:最长上升子序列和最长公共子序列
这两道题的解题思路,定义状态表示方式和推导状态转移方程的技巧常被用到其他题目中去
洛谷 B3637 最⻓上升⼦序列
洛谷 P1091 [NOIP2004 提⾼组] 合唱队形
最长上升子序列(数据范围小时用此)
时间复杂度是O(n平方)
链接:洛谷 B3637 最⻓上升⼦序列
要理解最长上升子序列是什么意思!!!
1.状态表示:
dp[i]表示:以i位置为结尾的所有子序列中,最长递增子序列的长度
2.状态转移方程:
根据子序列的构成方式进行分类讨论:第一种:子序列长度为1:此时的dp[i] = 1;
第二种: 子序列的长度大于1:设j为前面某一个数的下标
只要a[j]<a[i],i位置元素跟在j元素后面就可以形成递增序列
其dp[i] = max(dp[j]+1p,dp[i])
3.初始化:
每次填表的时候,先把这个位置的数改成最小的域值即可主要部分的代码展示:
int ret = 0;
for(int i=1;i<=n;i++)
{
dp[i]=1;
for(int j=1;j<i;j++){if(a[j]<a[i])dp[i] = max(dp[i],dp[j]+1); }ret = max(ret,dp[i])
}应用: 洛谷 P1091 [NOIP2004 提⾼组] 合唱队形
牛客网 【模板】最⻓上升⼦序列
最长上升子序列(数据范围大时用此)
时间复杂度时O(n*logn)
链接:牛客网 【模板】最⻓上升⼦序列
优化动态规划:
1.发现在考虑最长递增子序列长度时,只用关心现在长度和序列最后一个元素
因此仅需统计长度为x的所有递增序列中最后一个元素的最小值(创建数组去统计)
2.在统计过程中发现:
数组中的数呈现递增趋势,因为可以使用二分来查找插入位置
主要部分的代码展示:
for(int i =1;i<=n;i++)
{//处理边界情况if(len ==0||a[i]>f[len]) f[++len]=a[i];
else{//二分插入位置int l = 1,r = len;while(l<r){int mid = (l+r)/2;if(f[mid]>=a[i]) r = mid;else l =mid+1;}f[l] = a[i]} }牛客网 ⽜可乐和最⻓公共⼦序列
洛谷 P2758 编辑距离
牛可乐和最长公共子序列
链接:牛客网 ⽜可乐和最⻓公共⼦序列
1.状态表示:
dp[i][j]表示:
s1的[1,i]区间以及s2的[1,j]区间内的所有的子序列中,最长公共子序列的长度2.状态转移方程:
对于dp[i][j],我们可以根据s1[i]与s2[j]的字符分情况讨论:
第一种:两个字符相同 dp[i][j] = dp[i-1][j-1]+1
第二种:两个字符不同 有以下三种策略
a.去s1的[1,i-1]以及s2的[1,j]区间内找:此时最大长度为dp[i-1][j]
b.去s1的[1,i]以及s2的[1,j-1]区间内找:此时最大长度为dp[i][j-1]
c.去s1的[1,i-1]以及s2的[1,j-1]区间内找:此时最大长度为dp[i-1][j-1]
(发现c包含在a和b情况里)
然后要a,b中的最大值即可代码展示:
for(int i =1;i<=n;i++)
{for(int j = 1;j<=m;j++){if(s[i-1] == t[j-1])f[i][j] = f[i-1][j-1]+1;else f[i][j] = max(f[i-1],f[i][j-1])}}应用:洛谷 P2758 编辑距离
背包问题分类
01背包问题:没中物品只能选或不选(选0次或1次)
完全背包问题:每种物品可以选择无限次
多重背包问题:每种物品有数量限制
分治背包问题:物品被分为若干组,每组只能选一个物品
混合背包:以上四种背包问题混在一起
多维费用的背包问题:限定条件不止有体积,还会有其他因素(比如重量)
背包问题的三种限定情况:
1.体积不超过j->小于等于j->j>=v[i]
2.体积正好为j->恰好等于j->要判断f表中某些状态是否合法
3.体积至少为j->大于等于j->j<v[i]也是合法的,映射到0位置即可背包问题在求方案数时,要把不选的情况单独写出,然后从只选一个开始,不然套模板可能会错
例:洛谷 P1077 [NOIP2012 普及组] 摆花
洛谷 P1077 [NOIP2012 普及组] 摆花
01背包问题
牛客网 【模板】01背包
洛谷 P2946 [USACO09MAR] Cow Frisbee Team S
01背包中的最大价值问题:
模板题:牛客网 【模板】01背包
v[i]表示第i个的体积 w[i]表示第i个的价值
第一问:求这个背包至多能装多大价值的物品1.状态表示:
dp[i][j]表示:从前i个物品中挑选,总体积不超过j,所有的选法中,能挑选出来的最大价值
那么dp[n][v]就是我们要的结果
2.状态转移方程:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])
3.初始化:无
4.填表顺序:从上往下(二维一般都是从上往下) 从右往左代码表现:
for(int i = 1;i<=n;i++)
{ for(int j=0;j<=m;j++){f[i][j] = f[i-1][j];if(j>=v[i])f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);}
}
空间优化版:(熟练了之后,直接写此)for(int i = 1;i<=n;i++)
{ for(int j=m;j>=v[i];j--)//01背包空间优化要修改遍历顺序{f[j] = max(f[j],f[j-v[i]]+w[i]);}
}第二问:
若背包恰好装满,求至少能装多大价值
仅需要在第一问基础上修改一下初始化以及最终结果即可
1.初始化
把所有位置先设置成-0x3f3f3f3f;然后把dp[0][0]修改成0
2.最终结果
要多一步判断最后一个位置是不是小于0代码展现:
memset(f,-0x3f,sizeof f);//多了这个
for(int i = 1;i<=n;i++)
{ for(int j=0;j<=m;j++){f[i][j] = f[i-1][j];if(j>=v[i])f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);}
}
if(f[n][m]<0)cout<<0<<endl;//多了这个
else cout << f[n][m]<<endl;//多了这个
空间优化版:(熟练了之后,直接写此)
memset(f,-0x3f,sizeof f);for(int i = 1;i<=n;i++)
{ for(int j=m;j>=v[i];j--)//01背包空间优化要修改遍历顺序{f[j] = max(f[j],f[j-v[i]]+w[i]);}
}
if(f[m]<0)cout<<0<<endl;
else cout << f[m]<<endl;注意:有些题可能不能用这种空间优化,因为要用到之前的数据的多少不同了
例题:洛谷 P2946 [USACO09MAR] Cow Frisbee Team S
(这题还要注意的是状态表示不能搞能力值总和为j,要搞总和模之后为j,不然空间时间都易超)
洛谷 P1164 ⼩A点菜
01背包中的方案数问题:
题目链接:洛谷 P1164 ⼩A点菜
1.状态表示:
dp[i][j]表示:从前i个菜中挑选,总价钱恰好等于j,此时的总方案数
2.针对于a[i]选或不选,分两种情况讨论:
得:dp[i][j] = d[i-1][j]+d[i-1][j-a[i]]
注意第二个状态可能不存在,要注意判断一下j>=a[i]
3.初始化:
dp[0][0] = 1
完全背包问题
牛客网 【模板】完全背包
模板题:牛客网 【模板】完全背包
第一问:求这个背包至多能装多大价值的物品
1.状态表示:和01背包一样
2.状态转移方程:
dp[i][j] = max(dp[i-1][j],dp[i][j-v[i]]+w[i])
3.初始化:
从第二行开始存,第一行全初始化为0
4.没有空间优化时,是从上往下,从左往右第二问:若背包恰好装满,求至多能装多大价值的物品
改法跟01背包那里完全相同与01背包的不同点:在空间优化时,完全背包的遍历顺序还是从左往右
多重背包
牛客网 多重背包
例题: 牛客网 多重背包
小tip:不是所有的多重背包问题都能用二进制优化,而且优化版本的代码很长如果时间复杂度允许的情况下,能不优化就不优化
解法一:
1.状态表示:
dp[i][j]表示:
从前i个物品中挑选,总重量不超过j的情况下,最大的价值2.状态转移方程:
这里不能用完全背包的方式(不是指那个空间优化)去优化
只能硬分x[i]+1种情况(选0个到选x[i]个)
选x[i]个:价值为dp[i-1][j-x[i]*w[i]]+x[i]*v[i] 3.初始化:
全部初始化为04.填表顺序:
从上往下,从左往右
空间优化之后则是从右往左代码展现:
for(int i =1;i<=n;i++)for(int j= m;j>=0;j--)for(int k = 0;k<=x[i]&&k*w[i]<=j;k++)f[j] = max(f[j],f[j-k*w[i]]+k*v[i])解法二:转化为01背包问题
优化方式:用二进制将同种的x[i]个物品分组
(如果是求方案数的话,是不能用二进制去优化的,会多算几种)
把这x[i]个物品拆成一些二进制数再加上多出来的数此题的有100种不同物品的话
如果同种的物品最多能分成5份,则数组的N要取(100+10)*5//+10纯属个人习惯洛谷 P1077 [NOIP2012 普及组] 摆花
多重背包的方案数问题:
例题:洛谷 P1077 [NOIP2012 普及组] 摆花
也就状态转移方程和初始化改了一下
分组背包问题
洛谷 P1757 通天之分组背包
例题:洛谷 P1757 通天之分组背包
1.状态表示:
dp[i][j]表示从前i组中挑选物品,总重量不超过j的情况下,最大的价值2.状态转移方程:
根据第i组选什么物品,可以分若干情况讨论
这个在空间优化时,第二维也要从右到左
混合背包问题
洛谷 P1833 樱花
例题:洛谷 P1833 樱花
这个混合背包的话,分情况讨论是哪种背包就是
注意的点是:多重背包和01背包的代码具有可合并性
多维费用的背包问题
洛谷 P1910 L 国的战⽃之间谍
例题:洛谷 P1910 L 国的战⽃之间谍
这无非就是多加几维就行
eg:
状态表示:
dp[i][j][k]表示:
从前i个人中挑选,伪装能力不超过j,总工资不超过k,此时能获取到的最多资料总数
eg:像这种获取到的最多资料总数,能砍到的最多的树木这种一般不为限制条件,一般是所求的值
在空间优化时,也只能优化掉第一维(从前i个人中挑选--这个一般放第一维)
空间优化后,除了第一维的遍历顺序可能都需要发生变化
区间dp
区间dp是用区间的左右端点来描述状态,通过小区间的解来推导出大区间的解
核心思想:将大区间划分为小区间,其状态转移方程通常依赖于区间的划分点
常见的划分点的方式有两个:
1.基于区间的左右端点,分情况讨论
2.基于区间上的某一个点,划分成左右区间讨论
应用:在序列中只关心左右两端,大概率用区间dp
洛谷 P1435 [IOI2000] 回⽂字串
例题:洛谷 P1435 [IOI2000] 回⽂字串
1.状态表示:
dp[i][j]表示:
字符串[i,j]区间,变成回文串的最小插入次数
那么,dp[1][n]就是我们要的结果2.状态转移方程:
根据区间的左右端点,分情况讨论对于区间dp的填表顺序,一般用的是:
第一维循环:从小到大枚举区间长度len;第二维循环:枚举区间左端点i,然后计算出区间右端点j
j = i+len-1
这个len有时从1开始,有时从2开始,看题
eg:
for(int len = 1;len<=n;len++)for(int i = 1; i+len-1<=n;i++)
洛谷 P2858 [USACO06FEB] Treats for the Cows G/S
洛谷 P3146 [USACO16OPEN] 248 G
关于这里的状态转移方程:
1.如果划分点是基于区间的左右端点,分情况讨论
eg: 洛谷 P2858 [USACO06FEB] Treats for the Cows G/S先拿左边,然后去[i + 1, j] 区间获得最多的钱,
即a[i] × (n − len + 1) + dp[i + 1][j] 先拿右边,然后去[i,j-1]区间获得最多的钱
即a[j]*(n-len+1)+de[i][j-1]2.如果划分点是基于区间上的某一个点,划分成左右区间讨论
eg: 洛谷 P3146 [USACO16OPEN] 248 G根据最后一次合并的情况,可以把区间分成[i,k][k+1,j](划分点是k)
相关文章:
(蓝桥杯常考点)—动态规划(C/C++))
基础算法篇(5)(蓝桥杯常考点)—动态规划(C/C++)
文章目录 动态规划前言线性dp路径类dp经典线性dp背包问题分类01背包问题完全背包问题多重背包分组背包问题混合背包问题多维费用的背包问题区间dp 动态规划 前言 在竞赛中,如果遇到动态规划的题目,只要不是经典题型,那么大概率就是以压轴题的…...

MLLMS_KNOW尝鲜版
背景(个人流水账,可毫不犹豫跳过) 最近项目中有涉及到小物体检测的内容,昨天晚上讨论的时候有提出是否可以将关注区域放大的idea,不过后来没有就着这个东西深入,结果好巧不巧地,今天关注到这篇…...

《软件设计师》复习笔记(12.2)——成本管理、配置管理
目录 一、项目成本管理 1. 定义 2. 主要过程 3. 成本类型 4. 其他概念 真题示例: 二、软件配置管理 1. 定义 2. 主要活动 3. 配置项 4. 基线(Baseline) 5. 配置库类型 真题示例: 一、项目成本管理 1. 定义 在批准…...

《AI赋能职场:大模型高效应用课》第8课 AI辅助职场沟通与协作
【本课目标】 掌握AI辅助邮件、沟通话术的优化技巧。学习利用AI快速生成高效的会议纪要。通过实操演练,提升职场沟通效率与协作能力。 【准备工具】 DeepSeek大模型(deepseek.com)百度文心一言(yiyan.baidu.com) 一…...

Spring 中的 @Cacheable 缓存注解
1 什么是缓存 第一个问题,首先要搞明白什么是缓存,缓存的意义是什么。 对于普通业务,如果要查询一个数据,一般直接select数据库进行查找。但是在高流量的情况下,直接查找数据库就会成为性能的瓶颈。因为数据库查找的…...

settimeout和setinterval区别
1. setTimeout:单次延迟执行 语法: const timeoutId setTimeout(callback, delay, arg1, arg2, ...); 核心功能:在指定的 delay(毫秒)后,执行一次 callback 函数。 参数: callback&#x…...
睫毛和眼睛的渲染是正常的,而在 Play 模式下出现模糊)
UE5编辑器静止状态下(非 Play 模式)睫毛和眼睛的渲染是正常的,而在 Play 模式下出现模糊
这通常指向以下几个 运行时(Runtime) 特有的原因: 抗锯齿 (Anti-Aliasing) 方法,特别是 Temporal Anti-Aliasing (TAA): 这是最可能的原因。 UE5 默认启用的 TAA 通过混合多帧信息来平滑边缘和减少闪烁,尤其是在运动中…...

怎样选择适合网站的服务器带宽?
合适的服务器带宽对于网站的需求起着至关重要的作用,服务器带宽会直接影响到网站的访问速度和用户体验,本文将介绍一下企业该怎样选择适合网站需求的服务器带宽! 不同类型的网站对于服务器带宽的需求也是不同的,小型博客网站的访问…...

Kaamel隐私与安全分析报告:Microsoft Recall功能评估与风险控制
本报告对Microsoft最新推出的Recall功能进行了全面隐私与安全分析。Recall是Windows 11 Copilot电脑的专属AI功能,允许用户以自然语言搜索曾在电脑上查看过的内容。该功能在初次发布时因严重隐私和安全问题而备受争议,后经微软全面重新设计。我们的分析表…...

linux 4.14内核jffs2文件系统不自动释放空间的bug
前段时间在做spi-nor flash项目的时候,使用jffs2文件系统,发现在4.14内核下存在无法释放空间的bug,后来进行了修复,修复后功能正常,现将修复patch公开,供后来者学习: diff --git a/fs/jffs2/ac…...

Thymeleaf简介
在Java中,模板引擎可以帮助生成文本输出。常见的模板引擎包括FreeMarker、Velocity和Thymeleaf等 Thymeleaf是一个适用于Web和独立环境的现代服务器端Java模板引擎。 Thymeleaf 和 JSP比较: Thymeleaf目前所作的工作和JSP有相似之处,Thyme…...

uniapp中uni-easyinput 使用@input 不改变绑定的值
只允许输入数字和字母 使用input 正则replace后赋值给A 遇到问题: 当输入任意连续的非法字符时, 输入框不变. 直到输入一个合法字符非法字符才成功被过滤. <uni-forms-item label"纳税人识别号" name"number"><uni-easyinput v-model"numb…...

前端零基础入门到上班:Day7——表单系统实战全解析
🧩前端零基础入门到上班:Day7——表单系统实战全解析 ✅ 目标:不仅掌握 HTML 表单标签,更深入理解其在实战中的作用、验证方式、美化技巧与 JS 联动,为后续接入 Vue、后端接口打下坚实基础。 🌟 一、HTML 表…...

【特殊场景应对1】视觉设计:信息密度与美学的博弈——让简历在HR视网膜上蹦迪的科学指南
写在最前 作为一个中古程序猿,我有很多自己想做的事情,比如埋头苦干手搓一个低代码数据库设计平台(目前只针对写java的朋友),比如很喜欢帮身边的朋友看看简历,讲讲面试技巧,毕竟工作这么多年,也做到过高管,有很多面人经历,意见还算有用,大家基本都能拿到想要的offe…...

o3和o4-mini的升级有哪些亮点?
ChatGPT是基于OpenAI GPT系列的高性能对话生成AI,经过多代迭代不断提升自然语言理解和生成能力。 在过去的一年中,OpenAI先后发布了GPT-4、GPT‑4.1及多种mini版本,为不同使用场景提供灵活选择。 随着用户需求向更高效、更精准的推理和视觉…...

影楼精修行业浅见-序言
影楼及商业摄影行业对高效、智能化的图像精修需求日益增长。传统修图流程耗时长、人工成本高,且修图师水平参差不齐影响最终成片质量。AI驱动的影像精修软件通过自动化、批量处理和智能算法,显著提升了修片效率和一致性,成为影楼数字化升级的…...
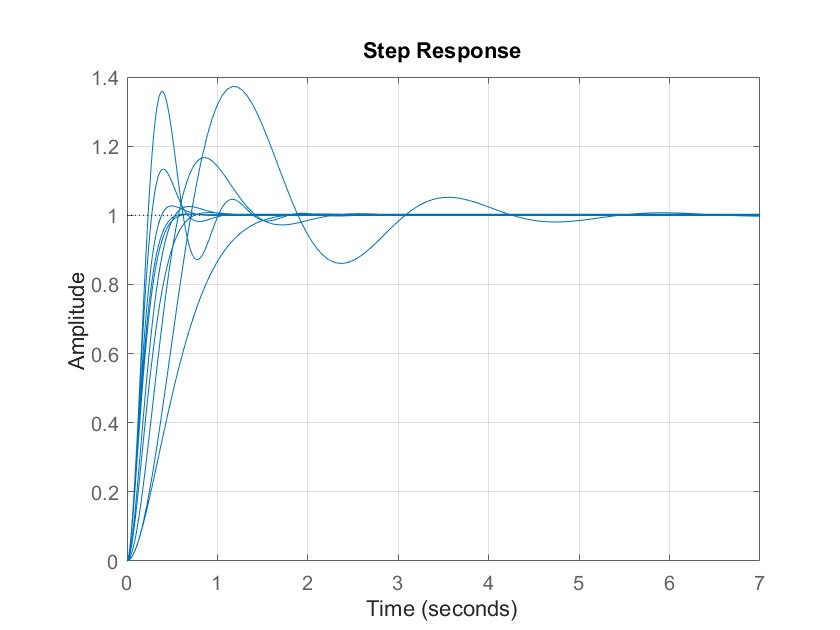
MATLAB 控制系统设计与仿真 - 36
鲁棒工具箱定义了个新的对象类ureal,可以定义在某个区间内可变的变量。 函数的调用格式为: p ureal(name,nominalvalue) % name为变量名,nominalValue为标称值,默认变化值为/-1 p ureal(name,nominalvalue,PlusMinus,plusminus) p ureal(name,nomin…...

Spring数据访问全解析:ORM整合与JDBC高效实践
目录 一、Spring ORM集成深度剖析 🌟 ORM模块架构设计 核心集成特性: 整合MyBatis示例配置: 二、Spring JDBC高效实践指南 🌟 传统JDBC vs Spring JDBC对比 🌟 JdbcTemplate核心操作示例 批量操作优化…...

【HCIA】使用Access port实现简易的VLAN间通信
前言 当我们拥有一台三层交换机与两个vlan,我们可以使用简易的Vlanif配置实现VLAN间通信。 文章目录 前言1. 拓扑图2. 配置交换机3. 配置PC1与PC2的网络4. port link-type后记修改记录 1. 拓扑图 2. 配置交换机 <Huawei>system-view [Huawei]undo info-cent…...

6.VTK 颜色
文章目录 概念RGB示例HSV示例 概念 RGB颜色系统:通过红(R)、绿(G)、蓝(B)三个颜色分量的组合来定义颜色。每个分量的取值范围是0到1,其中(0, 0, 0)代表黑色,而(1, 1, 1)代表白色。可以使用vtkProperty::SetColor(r, g, b)方法为Actor设置颜色…...

shiro使用
shiro是apache提供的一种安全框架。他可以将登录,权限这一方面简单化。 使用shiro需要引入 <dependency><groupId>org.apache.shiro</groupId><artifactId>shiro-core</artifactId><version>1.9.0</version></depend…...

光谱相机的成像方式
光谱相机的成像方式决定了其如何获取物体的空间与光谱信息,核心在于分光技术与扫描模式的结合。以下是主要成像方式的分类解析: 一、滤光片切换型 1. 滤光片轮(Filter Wheel) 原理:通过旋转装有多个窄带…...

浅析MySQL事务锁
在 MySQL 中,事务锁是用于确保数据一致性和并发控制的重要机制。事务锁可以帮助防止多个事务同时修改同一数据,从而避免数据不一致和脏读、不可重复读、幻读等问题。 以下是 MySQL 事务锁的关键点总结: 事务锁:用于确保数据一致性和并发控制。锁的类型: 行级锁:InnoDB,粒…...

算法-链表
小细节 初始化问题 我们这样子new一个ListNode 它里面的默认值是0,所以我们不能这样 如果我们为空,我们要返回null 节点结束条件判断(多创建节点问题) 参考示例3217 解析: 我的答案是多了一个无用节点 这是因为我每…...

ON DUPLICATE KEY UPDATE 更底层解释它的优势
从更底层来看,ON DUPLICATE KEY UPDATE 的优势主要源于以下几个方面: 1. 减少网络往返次数 先查询再更新:这种方式需要客户端和数据库服务器之间进行多次网络通信。首先,客户端发送一个 SELECT 查询请求,然后等待服务…...

3.8/Q1,GBD数据库最新文章解读
文章题目:Regional and National Burden of Traumatic Brain Injury and Spinal Cord Injury in North Africa and Middle East Regions, 1990-2021: A Systematic Analysis for The Global Burden of Disease Study 2021 DOI:10.1007/s44197-025-00372-…...

51单片机实验二:数码管静态显示
目录 一、实验环境与实验器材 二、实验内容及实验步骤 1.单个数码管显示 2.六个数码管依次从0~F变换显示 3.proteus仿真 一、实验环境与实验器材 环境:Keli,STC-ISP烧写软件,Proteus. 器材:TX-1C单片机(STC89C52RC…...

Linux驱动开发进阶(八)- GPIO子系统BSP驱动
文章目录 1、前言2、pinctrl子系统3、pinctrl bsp驱动4、gpio子系统5、gpio bsp驱动 1、前言 学习参考书籍以及本文涉及的示例程序:李山文的《Linux驱动开发进阶》本文属于个人学习后的总结,不太具备教学功能。 2、pinctrl子系统 在讨论gpio子系统时&…...

【Windows】安装或者点击OneDrive没有任何反应的解决方案
一些Windows企业版或者神州网信政府版的策略会禁止使用OneDrive,双击OneDrive安装程序或者点击OneDrive软件会没有任何反应。通过下面的设置可以解除相关的限制。 1、修改注册表 打开注册表管理器。依次HKEYLOCAL_MACHINE\Software\Policies\Microsoft\Windows\One…...

Android tinyalsa库函数剖析
1. PCM 流控制函数 打开、关闭及状态检查 pcm_open(unsigned int card, unsigned int device, unsigned int flags, struct pcm_config *config) 打开指定声卡(card)和设备(device)的 PCM 流。 flags 参数确定流的方向࿱…...
