力扣经典拓扑排序
207. 课程表(Course Schedule)
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则必须先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对互不相同
拓扑排序
为了解决课程表问题,可以使用拓扑排序来判断是否存在环。如果存在环,则无法完成所有课程学习,否则可以完成。
拓扑排序是一种将有向无环图(DAG)中的顶点排成一个线性序列的方法。如果图中存在环,则无法进行拓扑排序。
具体步骤如下:
- 构建图和入度表:根据先修课程关系构建图,并记录每个课程的入度。
- 使用队列进行拓扑排序:将所有入度为
0的课程加入队列,然后逐步减少相邻课程的入度。如果一个课程的入度变为0,将其加入队列。 - 判断是否完成所有课程:如果最终排序的课程数量等于总课程数,则可以完成所有课程学习。
C++ ACM 模式实现
#include <iostream>
#include <vector>
#include <queue>
using namespace std;bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {// 构建图和入度表vector<vector<int>> graph(numCourses);vector<int> inDegree(numCourses, 0);for (const auto& prereq : prerequisites) {int to = prereq.first;int from = prereq.second;graph[from].push_back(to);inDegree[to]++;}// 拓扑排序queue<int> q;for (int i = 0; i < numCourses; ++i) {if (inDegree[i] == 0) {q.push(i);}}int count = 0;while (!q.empty()) {int node = q.front();q.pop();count++;for (int neighbor : graph[node]) {inDegree[neighbor]--;if (inDegree[neighbor] == 0) {q.push(neighbor);}}}return count == numCourses;
}int main() {int numCourses = 2;vector<pair<int, int>> prerequisites = {{1, 0}};bool result = canFinish(numCourses, prerequisites);cout << (result ? "true" : "false") << endl;return 0;
}
代码说明
-
构建图和入度表:
graph是邻接表,表示每个课程的后续课程。inDegree记录每个课程的入度(即需要先修的课程数量)。
-
拓扑排序:
- 使用队列存储所有入度为
0的课程。 - 每次取出一个课程,减少其后续课程的入度,如果后续课程的入度变为0,则加入队列。
- 使用队列存储所有入度为
-
判断是否完成所有课程:
- 如果最终完成的课程数量等于总课程数,则返回
true,否则返回false。
- 如果最终完成的课程数量等于总课程数,则返回
复杂度
- 时间复杂度:
O(V + E),其中V是课程数,E是先修课程关系数。 - 空间复杂度:
O(V + E),用于存储图和入度表。
210. 课程表 II(Course Schedule II)
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites,其中 prerequisites[i] = [ai, bi],表示在选修课程 ai 前必须先选修 bi。
例如,想要学习课程 0,你需要先完成课程 1,我们用一个匹配来表示:[0, 1]。
请你返回为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回任意一种就可以。如果不可能完成所有课程,返回一个空数组。
示例 1
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 `[0,1]`。
示例 2
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2,并且课程 1 和课程 2 都应该排在课程 0 之后。因此,一个正确的课程顺序是 `[0,1,2,3]`。另一个正确的排序是 `[0,2,1,3]`。
示例 3
输入:numCourses = 1, prerequisites = []
输出:[0]
提示
1 <= numCourses <= 2000
0 <= prerequisites.length <= numCourses * (numCourses - 1)
prerequisites[i].length == 2
0 <= ai, bi < numCourses
ai != bi
所有 [ai, bi] 互不相同
拓扑排序+输出
- 构建图和入度表:根据先修课程关系构建图,同时记录每个课程的入度(即需要先修的课程数量)。
- 初始化队列:将所有入度为
0的课程加入队列,这些课程可以立即学习。 - 拓扑排序:每次从队列中取出一个课程,将其加入结果列表。然后遍历该课程的所有后续课程,将它们的入度减
1。如果某个后续课程的入度变为0,则将其加入队列。 - 判断结果:如果结果列表的长度等于总课程数,则说明所有课程都可以完成,返回结果列表;否则,返回空数组。
C++ ACM 模式实现
#include <iostream>
#include <vector>
#include <queue>
using namespace std;vector<int> findOrder(int numCourses, vector<pair<int, int>>& prerequisites) {vector<int> result;vector<vector<int>> graph(numCourses);vector<int> inDegree(numCourses, 0);// 构建图和入度表for (const auto& prereq : prerequisites) {int to = prereq.first;int from = prereq.second;graph[from].push_back(to);inDegree[to]++;}// 初始化队列,添加所有入度为0的课程queue<int> q;for (int i = 0; i < numCourses; ++i) {if (inDegree[i] == 0) {q.push(i);}}// 拓扑排序while (!q.empty()) {int course = q.front();q.pop();result.push_back(course);for (int nextCourse : graph[course]) {inDegree[nextCourse]--;if (inDegree[nextCourse] == 0) {q.push(nextCourse);}}}// 如果结果列表的长度等于总课程数,说明可以完成所有课程if (result.size() == numCourses) {return result;} else {return {};}
}int main() {int numCourses = 4;vector<pair<int, int>> prerequisites = {{1, 0}, {2, 0}, {3, 1}, {3, 2}};vector<int> result = findOrder(numCourses, prerequisites);if (!result.empty()) {cout << "学习顺序为: ";for (int course : result) {cout << course << " ";}cout << endl;} else {cout << "无法完成所有课程" << endl;}return 0;
}
代码说明
- 构建图和入度表:
- 邻接表
graph用于表示每个课程的后续课程。 - 入度表
inDegree用于记录每个课程的入度(需要先修的课程数量)。
- 邻接表
- 拓扑排序:
- 使用队列存储所有入度为0的课程。
- 每次取出一个课程,将其加入结果列表,并减少其后续课程的入度。
- 判断结果:
- 如果结果列表的长度等于总课程数,说明所有课程都可以完成,返回结果列表。
- 否则,返回空数组,表示无法完成所有课程。
复杂度
- 时间复杂度:O(V + E),其中 V 是课程数,E 是先修课程关系数。
- 空间复杂度:O(V + E),用于存储图和入度表。
269. 火星词典(Alien Dictionary)
现有一种使用英语字母的火星语言,这门语言的字母顺序对你来说是未知的。给你一个来自这种外星语言字典的字符串列表 words,words 中的字符串已经按这门新语言的字典序进行了排序。
- 如果这种说法是错误的,并且给出的 words 不能对应任何字母的顺序,则返回 “”。
- 否则,返回一个按新语言规则的字典递增顺序排序的独特字符串。如果有多个解决方案,则返回其中任意一个。
示例 1
输入:words = ["wrt","wrf","er","ett","rftt"]
输出:"wertf"
示例 2
输入:words = ["z","x"]
输出:"zx"
示例 3
输入:words = ["z","x","z"]
输出:""
解释:不存在合法字母顺序,因此返回 ""。
提示
1 <= words.length <= 100
1 <= words[i].length <= 100
words[i] 仅由小写英文字母组成
拓扑排序+字符
把每个单词看作由字符组成的序列。按字典序排列的单词列表中,相邻两个单词的第一个不同字符确定了这两个字符的先后顺序。比如单词 a 和单词 b,假设它们前面几个字符都相同,第 k 个字符 a[k] 和 b[k] 不同,那么 a[k] 应该在 b[k] 之前。
基于这样的规则,遍历给定的单词列表,对相邻单词进行比较,找到每对相邻单词中第一个不同的字符对,从而确定字符之间的顺序关系,并构建一个有向图来表示这些字符的先后顺序关系。
同时,要记录每个字符的入度,入度表示有多少个字符需要排在这个字符之前。
利用拓扑排序算法来确定字符的顺序。
- 初始化一个队列,将所有入度为
0的字符加入队列。这些字符没有其他字符需要排在它们前面,可以作为字典序的开头部分。 - 每次从队列中取出一个字符,将其加入结果序列。然后,遍历该字符在图中的所有相邻字符(即需要排在这个字符之后的字符),将这些相邻字符的入度减
1。如果某个相邻字符的入度减到0,则将其加入队列。 - 重复上述过程,直到队列为空。
最后检查结果序列是否包含了所有出现过的字符。如果包含,则说明存在一种合法的字典序,该序列为所求结果之一;如果不包含,说明图中存在环,无法确定合法的字典序,返回空字符串。
以下是示例 1 的详细推导过程:
输入:words = ["wrt","wrf","er","ett","rftt"]
比较相邻单词:
"wrt" 和 "wrf":第一个不同的字符是 t 和 f,所以 t 应该在 f 之前。
"wrf" 和 "er":第一个字符 w 和 e,w 应该在 e 之前。
"er" 和 "ett":第一个不同的字符是 r 和 t,r 应该在 t 之前。
"ett" 和 "rftt":第一个字符 e 和 r,e 应该在 r 之前。
构建图后,进行拓扑排序得到一个可能的顺序 "wertf"。
c++ ACM 模式实现
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <unordered_set>
using namespace std;string alienOrder(vector<string>& words) {// 构建图和入度表unordered_map<char, unordered_set<char>> adj;unordered_map<char, int> indegree;// 初始化所有出现的字符for (string word : words) {for (char c : word) {if (!adj.count(c)) {adj[c] = unordered_set<char>();indegree[c] = 0;}}}// 构建图和入度表for (int i = 0; i < words.size() - 1; i++) {string word1 = words[i];string word2 = words[i + 1];int len = min(word1.size(), word2.size());for (int j = 0; j < len; j++) {if (word1[j] != word2[j]) {// word1[j] 应该在 word2[j] 之前if (!adj[word1[j]].count(word2[j])) {adj[word1[j]].insert(word2[j]);indegree[word2[j]]++;}break; // 只比较第一个不同的字符}}}// 拓扑排序queue<char> q;// 初始化队列,将入度为 0 的字符加入队列for (auto& pair : indegree) {if (pair.second == 0) {q.push(pair.first);}}string result;while (!q.empty()) {char c = q.front();q.pop();result += c;// 遍历相邻字符并更新入度for (char neighbor : adj[c]) {indegree[neighbor]--;if (indegree[neighbor] == 0) {q.push(neighbor);}}}// 检查结果是否包含所有字符if (result.size() != adj.size()) {return ""; // 存在环,无法确定字典序}return result;
}int main() {vector<string> words1 = {"wrt", "wrf", "er", "ett", "rftt"};cout << alienOrder(words1) << endl; // 输出 "wertf"vector<string> words2 = {"z", "x"};cout << alienOrder(words2) << endl; // 输出 "zx"vector<string> words3 = {"z", "x", "z"};cout << alienOrder(words3) << endl; // 输出 ""return 0;
}
代码说明
-
构建图和入度表 :
- 使用
unordered_map<char, unordered_set<char>> adj存储图的邻接表,其中键是字符,值是该字符后面可以跟的字符集合。 - 使用
unordered_map<char, int> indegree存储每个字符的入度,表示有多少个字符需要排在这个字符之前。 - 遍历
words列表中的所有单词,初始化所有出现的字符到图和入度表中。
- 使用
-
比较相邻单词构建图关系 :
- 遍历
words列表中的相邻单词对,比较每对单词的第一个不同字符。 - 根据第一个不同字符确定字符之间的顺序关系,并更新图和入度表。
- 遍历
-
拓扑排序 :
- 初始化一个队列,将所有入度为 0 的字符加入队列。
- 每次取出队列中的一个字符,将其加入结果字符串。然后遍历该字符的所有相邻字符,更新它们的入度。如果某个相邻字符的入度变为 0,则将其加入队列。
-
检查结果的有效性 :
- 如果结果字符串的长度等于图中所有字符的数量,则说明存在一种合法的字典序,返回结果字符串。
- 否则,说明图中存在环,无法确定合法的字典序,返回空字符串。
代码错误
当输入为 ["abc","ab"] 时,我们比较这两个单词:
- 第一个单词是
"abc",第二个单词是"ab"。 - 两个单词的前两个字符
"ab"相同。 - 第一个单词在第三个字符处多了一个
'c',而第二个单词已经结束。
根据字典序规则,较短的单词应该排在较长的单词前面,当且仅当较短的单词是较长单词的前缀。在这个例子中,第二个单词 "ab" 是第一个单词 "abc" 的前缀,但在这个输入中,较短的单词出现在较长的单词之后,这违反了字典序规则。因此,不存在合法的字典序。
在之前的代码实现中,我们需要处理这种情况。具体来说,我们需要在比较相邻单词时,检查是否会出现短单词在长单词后面的情况,并且短单词是长单词的前缀。如果是这样,则直接返回空字符串 ""。
代码修改
检查非法情况 :在比较相邻单词时,如果发现短单词在长单词之后且短单词是长单词的前缀,则直接返回空字符串 ""。
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <unordered_set>
using namespace std;string alienOrder(vector<string>& words) {// 构建图和入度表unordered_map<char, unordered_set<char>> adj;unordered_map<char, int> indegree;// 初始化所有出现的字符for (string word : words) {for (char c : word) {if (!adj.count(c)) {adj[c] = unordered_set<char>();indegree[c] = 0;}}}// 构建图和入度表for (int i = 0; i < words.size() - 1; i++) {string word1 = words[i];string word2 = words[i + 1];int len = min(word1.size(), word2.size());bool found = false;for (int j = 0; j < len; j++) {if (word1[j] != word2[j]) {// word1[j] 应该在 word2[j] 之前if (!adj[word1[j]].count(word2[j])) {adj[word1[j]].insert(word2[j]);indegree[word2[j]]++;}found = true;break; // 只比较第一个不同的字符}}// 如果没有找到不同的字符且 word1 更长,则无法确定字典序if (!found && word1.size() > word2.size()) {return "";}}// 拓扑排序queue<char> q;// 初始化队列,将入度为 0 的字符加入队列for (auto& pair : indegree) {if (pair.second == 0) {q.push(pair.first);}}string result;while (!q.empty()) {char c = q.front();q.pop();result += c;// 遍历相邻字符并更新入度for (char neighbor : adj[c]) {indegree[neighbor]--;if (indegree[neighbor] == 0) {q.push(neighbor);}}}// 检查结果是否包含所有字符if (result.size() != adj.size()) {return ""; // 存在环,无法确定字典序}return result;
}int main() {vector<string> words1 = {"abc", "ab"};cout << alienOrder(words1) << endl; // 输出 ""return 0;
}
310. 最小高度树(Minimum Height Trees)
树是一个无向图,其中任何两个顶点只通过一条路径连接。换句话说,任何一个没有简单环路的连通图都是一棵树。
给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为最小高度树。
请你找到所有的最小高度树并按任意顺序返回它们的根节点标签列表。
树的高度是指根节点和叶子节点之间最长向下路径上边的数量。
示例 1

输入:n = 4, edges = [[1,0],[1,2],[1,3]]
输出:[1]
解释:如图所示,当根是标签为 1 的节点时,树的高度是 1 ,这是唯一的最小高度树。
示例 2

输入:n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出:[3,4]
提示
1 <= n <= 2 * 10^4
edges.length == n - 1
0 <= ai, bi < n
ai != bi
所有 (ai, bi) 互不相同
给定的输入保证是一棵树,并且不会有重复的边
拓扑排序的去叶法
要解决最小高度树问题,可以使用拓扑排序中的“去叶法”(摘叶子法)。
这种方法通过不断地去除树的叶子节点来找到树的中心,中心节点即为最小高度树的根节点。
树的中心通常位于树的中间位置,对于树的高度来说,以中心节点为根可以保证树的高度最小。通过不断地去除叶子节点(度为 1 的节点),直到剩下最后 1 或 2 个节点,这些节点即为所求的最小高度树的根节点。
- 构建图的邻接表:表示树的结构。
- 初始化叶子节点队列:所有度为
1的节点(叶子节点)加入队列。 - 逐层去除叶子节点:每次从队列中取出一个节点,将其相邻节点的度减
1。如果相邻节点的度变为1,则将其加入队列。 - 记录剩余节点:当剩余节点数不超过
2时,这些节点即为所求。
c++ ACM 模式实现
#include <vector>
#include <queue>
using namespace std;vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {if (n == 1) return {0}; // 特殊情况处理vector<vector<int>> adj(n);vector<int> degree(n, 0);for (auto& edge : edges) {int a = edge[0], b = edge[1];adj[a].push_back(b);adj[b].push_back(a);degree[a]++;degree[b]++;}queue<int> q;for (int i = 0; i < n; i++) {if (degree[i] == 1) {q.push(i);}}vector<int> result;while (!q.empty()) {result.clear(); // 清空上一轮的节点int size = q.size();for (int i = 0; i < size; i++) {int u = q.front();q.pop();result.push_back(u);for (int v : adj[u]) {degree[v]--;if (degree[v] == 1) {q.push(v);}}}}return result;
}
代码说明
- 构建邻接表:用于表示树的结构,每个节点保存其相邻节点列表。
- 初始化叶子节点队列:所有度为
1的节点(叶子节点)加入队列。 - 逐层去除叶子节点:每次处理当前层的所有叶子节点,将其相邻节点的度减
1。如果相邻节点的度变为1,则加入队列。 - 记录剩余节点:当队列处理完一层后,当前层的节点即为当前剩余的节点。最后剩下的
1或2个节点即为所求。
444. 序列重建(Sequence Reconstruction)
给定一个长度为 n 的整数数组 nums,其中 nums 是范围为 [1, n] 的整数的排列。还提供了一个 2D 整数数组 sequences,其中 sequences[i] 是 nums 的子序列。
检查 nums 是否是唯一的最短超序列。最短超序列是长度最短的序列,并且所有序列 sequences[i] 都是它的子序列。对于给定的数组 sequences,可能存在多个有效的超序列。
如果 nums 是序列的唯一最短超序列,则返回 true,否则返回 false。
示例 1
输入:nums = [1,2,3], sequences = [[1,2],[1,3]]
输出:false
解释:有两种可能的超序列:[1,2,3] 和 [1,3,2]。
示例 2
输入:nums = [1,2,3], sequences = [[1,2]]
输出:false
解释:最短可能的超序列为 [1,2]。
示例 3
输入:nums = [1,2,3], sequences = [[1,2],[1,3],[2,3]]
输出:true
解释:最短可能的超序列为 [1,2,3]。
提示
n == nums.length
1 <= n <= 10^4
nums 是 [1, n] 范围内所有整数的排列
1 <= sequences.length <= 10^4
1 <= sequences[i].length <= 10^4
1 <= sum(sequences[i].length) <= 10^5
1 <= sequences[i][j] <= n
sequences 的所有数组都是唯一的
sequences[i] 是 nums 的一个子序列
拓扑排序+唯一性
要实现这个算法,可以使用拓扑排序来构建一个唯一的最短超序列。具体来说,我们需要通过给定的 sequences 构建一个有向图,然后通过拓扑排序来检查是否存在唯一的超序列。
- 构建图和入度表:根据
sequences构建一个有向图,其中边表示元素之间的顺序关系。同时维护一个入度表,记录每个节点的入度。 - 拓扑排序:通过
Kahn算法进行拓扑排序。在每一步中,如果队列中有多个节点,说明存在多个可能的超序列,因此nums不是唯一的最短超序列。 - 验证超序列:拓扑排序的结果需要与
nums进行比较,确保它们一致。
C++ ACM 模式实现
#include <vector>
#include <iostream>
#include <queue>
using namespace std;bool sequenceReconstruction(vector<int> &nums, vector<vector<int>> &sequences)
{vector<vector<int>> graph(nums.size() + 1);vector<int> indegree(nums.size() + 1, 0);for (auto &seq : sequences){for (int i = 1; i < seq.size(); i++){graph[seq[i - 1]].push_back(seq[i]);indegree[seq[i]]++;}}queue<int> q;for (int i = 1; i < nums.size() + 1; i++){if (indegree[i] == 0){q.push(i);}}vector<int> res;while (!q.empty()){if (q.size() > 1){return false;}int cur = q.front();q.pop();res.push_back(cur);for (auto &node : graph[cur]){indegree[node]--;if (indegree[node] == 0){q.push(node);}}}return res == nums;
}int main()
{vector<int> nums = {1, 2, 3};vector<vector<int>> sequences = {{1, 2}, {1, 3}, {2, 3}};bool result = sequenceReconstruction(nums, sequences);if (result){cout << "true" << endl;}else{cout << "false" << endl;}return 0;
}
代码说明
- 构建图和入度表:
adj是邻接表,表示图的结构。indegree记录每个节点的入度。 - 初始化图和入度表:遍历
nums初始化图和入度表。 - 构建图和入度表:遍历
sequences中的每个子序列,构建图并更新入度表。 - 拓扑排序:使用
Kahn算法进行拓扑排序。如果在排序过程中队列中有多个节点,说明存在多个可能的超序列,返回false。 - 验证超序列:拓扑排序的结果需要与
nums相同,否则返回false。
推荐一下
https://github.com/0voice
相关文章:

力扣经典拓扑排序
207. 课程表(Course Schedule) 你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出,其中 prerequisites[i] [ai, bi] ,表…...

Session与Cookie的核心机制、用法及区别
Python中Session与Cookie的核心机制、用法及区别 在Web开发中,Session和Cookie是两种常用的用于跟踪用户状态的技术。它们在实现机制、用途和安全性方面都有显著区别。本文将详细介绍它们的核心机制、用法以及它们之间的主要区别。 一、Cookie的核心机制与用法 1…...

【第16届蓝桥杯C++C组】--- 2025
hello呀,小伙伴们,这是第16届蓝桥杯第二道填空题,和第一道填空题一样也是十分基础的题目,有C语言基础基本都可以解,下面我讲讲我当时自己的思路和想法,如果你们有更优化的代码和思路,也可以分享…...

前端基础之《Vue(7)—生命周期》
一、什么是生命周期 1、生命周期 组件从“生”到“死”的全过程。 每一个组件都有生命周期。 2、生命周期四大阶段 创建阶段:beforeCreate、created 挂载阶段:beforeMount、mounted 更新阶段:beforeUpdate、updated 销毁阶段:be…...

C语言高频面试题——指针数组和数组指针
指针数组和数组指针是 C/C 中容易混淆的两个概念,以下是详细对比: 1. 指针数组(Array of Pointers) 定义:一个数组,其元素是 指针类型。语法:type* arr[元素个数]; 例如:int* ptr_a…...

Linux服务器配置Anaconda环境、Pytorch库(图文并茂的教程)
引言:为了方便后续新进组的 师弟/师妹 使用课题组的服务器,特此编文(ps:我导从教至今四年,还未招师妹) ✅ NLP 研 2 选手的学习笔记 笔者简介:Wang Linyong,NPU,2023级&a…...

Android端使用无障碍服务实现远程、自动刷短视频
最近在做一个基于无障碍自动刷短视频的APP,需要支持用任意蓝牙遥控器远程控制, 把无障碍服务流程大致研究了一下,从下面3个部分做一下小结。 1、需要可调整自动上滑距离和速度以适配不同的屏幕和应用 智能适配99%机型,滑动参数可…...

搭建用友U9Cloud ERP及UAP IDE环境
应用环境 Microsoft Windows 10.0.19045.5487 x64 专业工作站版 22H2Internet Information Services - 10.0.19041.4522Microsoft SQL Server 2019 - 15.0.2130.3 (X64)Microsoft SQL Server Reporing Services 2019 - 15.0.9218.715SQL Server Management Studio -18.6 laster…...

多模态大语言模型arxiv论文略读(二十九)
Temporal Insight Enhancement: Mitigating Temporal Hallucination in Multimodal Large Language Models ➡️ 论文标题:Temporal Insight Enhancement: Mitigating Temporal Hallucination in Multimodal Large Language Models ➡️ 论文作者:Li Su…...

Java开发中的设计模式之观察者模式详细讲解
观察者模式(Observer Pattern)是一种行为型设计模式,它定义了对象之间的一种一对多的依赖关系。当一个对象的状态发生改变时,所有依赖于它的对象都会自动收到通知并更新。这种模式在Java开发中非常常见,尤其是在事件驱…...

基于SpringAI Alibaba实现RAG架构的深度解析与实践指南
一、RAG技术概述 1.1 什么是RAG技术 RAG(Retrieval-Augmented Generation)检索增强生成是一种将信息检索技术与生成式AI相结合的创新架构。它通过以下方式实现智能化内容生成: 知识检索阶段:从结构化/非结构化数据源中检索相关…...

卷积神经网络(CNN)详解
文章目录 引言1.卷积神经网络(CNN)的诞生背景2.卷积神经网络(CNN)介绍2.1 什么是卷积神经网络?2.2 卷积神经网络(CNN)的基本特征2.2.1 局部感知(Local Connectivity)2.2.…...

element-plus添加暗黑模式
main.ts文件 //引入暗黑模式样式 import "element-plus/theme-chalk/dark/css-vars.css"; style.scss文件 // 设置默认主题色 :root {--base-menu-min-width: 80px;--el-color-primary-light-5: green !important;--route--view--background-color: #fff !import…...

【SF顺丰】顺丰开放平台API对接(注册、API测试篇)
1.注册开发者账号 注册地址:顺丰企业账户中心 2.登录开发平台 登录地址:顺丰开放平台 3.开发者对接 点击开发者对接 4.创建开发对接应用 开发者应用中“新建应用”创建应用,最多创建应用限制数量5个 注意:需要先复制保存生产校验…...

VisualSVN过期后的解决方法
作为一款不错的源代码管理软件,svn还是有很多公司使用的。在vs中使用svn,大家一般用的都是VisualSVN插件。在30天试用期过后,它就不能被免费使用了。下面给大家讲如何免费延长过期时间(自定义天数,可以设定一个很大的值…...

代码随想录算法训练营第二十一天
LeetCode题目: 93. 复原 IP 地址78. 子集90. 子集 II2364. 统计坏数对的数目 其他: 今日总结 往期打卡 93. 复原 IP 地址 跳转: 93. 复原 IP 地址 学习: 代码随想录公开讲解 问题: 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能…...

21. git apply
基本概述 git apply 的作用是:应用补丁文件 基本用法 1.命令格式 git apply [选项] <补丁文件>2.应用补丁 git apply patchfile.patch将补丁应用到工作目录,但不会自动添加到暂存区(需手动 git add) 常用选项 1.检查…...

DeepSeek智能时空数据分析(二):3秒对话式搞定“等时圈”绘制
序言:时空数据分析很有用,但是GIS/时空数据库技术门槛太高 时空数据分析在优化业务运营中至关重要,然而,三大挑战仍制约其发展:技术门槛高,需融合GIS理论、SQL开发与时空数据库等多领域知识;空…...

STM32学习2
一、OLED 1.1 OLED介绍 OLED(Organic Light Emitting Diode):有机发光二极管 OLED显示屏:性能优异的新型显示屏,具有功耗低、相应速度快、宽视角、轻薄柔韧等特点 0.96寸OLED模块:小巧玲珑、占用接口少…...

数据处理: 亲和聚类
Affinity Propagation(亲和传播)是一种基于"消息传递"概念的聚类算法,由Brendan Frey和Delbert Dueck于2007年提出。与K-Means等需要预先指定簇数量的算法不同,Affinity Propagation能够自动确定最佳簇的数量࿰…...

LabVIEW液压系统远程监控与故障诊断
开发了一种基于LabVIEW的远程液压系统监控解决方案,通过先进的数据采集与分析技术,有效提升工程机械的运作效率和故障响应速度。该系统结合现场硬件设备和远程监控软件,实现了液压系统状态的实时检测和故障诊断,极大地提升了维护效…...

Idea中实用设置和插件
目录 一、Idea使用插件 1.Fitten Code智能提示 2.MyBatisCodeHelperPro 3.HighlightBracketPair 4.Rainbow Brackets Lite 5.GitToolBox(存在付费) 6.MavenHelperPro 7.Search In Repository 8.VisualGC(存在付费) 9.vo2dto 10.Key Promoter X 11.CodeGlance…...

安卓处理登录权限问题
在安卓应用中实现登录权限控制,需确保用户登录后才能访问特定功能。以下是分步骤的解决方案: 1. 保存和检查登录状态 使用安全存储保存登录凭证: 推荐使用 EncryptedSharedPreferences 存储敏感信息(如Token、用户ID)…...

Java写数据结构:栈
1.概念: 一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压栈:栈的插…...

使用Unity Cache Server提高效率
2021年1月20日19:04:28 1 简介 Unity Cache Server,翻译过来就是Unity缓存服务器 1.1 缓存服务器の官方介绍 Unity 有一个完全自动的资源管线。每当修改 .psd 或 .fbx 文件等源资源时,Unity 都会检测到更改并自动将其重新导入。随后,Unity 以内部格式存储从文件导入的数…...

29个常见的Terraform 面试问题
问题 1:假设您使用 Terraform 创建了一个 EC2 实例,创建完成后,您从状态文件中删除了该条目,那么运行 Terraform Apply 命令时会发生什么? 由于我们已从该状态文件中删除了该条目,因此 Terraform 将不再管…...

机器学习-08-推荐算法-案例
总结 本系列是机器学习课程的系列课程,主要介绍机器学习中关联规则 参考 机器学习(三):Apriori算法(算法精讲) Apriori 算法 理论 重点 MovieLens:一个常用的电影推荐系统领域的数据集 23张图&#x…...
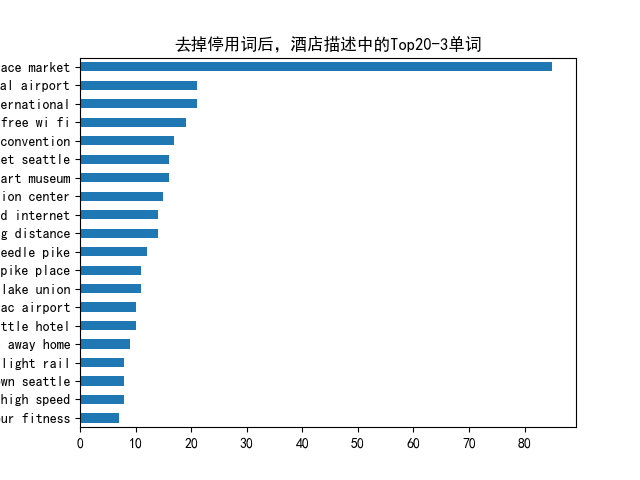
LLM中的N-Gram、TF-IDF和Word embedding
文章目录 1. N-Gram和TF-IDF:通俗易懂的解析1.1 N-Gram:让AI学会"猜词"的技术1.1.1 基本概念1.1.2 工作原理1.1.3 常见类型1.1.4 应用场景1.1.5 优缺点 1.2 TF-IDF:衡量词语重要性的尺子1.2.1 基本概念1.2.2 计算公式1.2.3 为什么需…...

uniapp APP端 DOM生成图片保存到相册
<template> <view class"container" style"padding-bottom: 30rpx;"> <view class"hdbg pr w100 " style"height: 150rpx;"> <top-bar content分享 Back"Back"></top-b…...

Office文件内容提取 | 获取Word文件内容 |Javascript提取PDF文字内容 |PPT文档文字内容提取
关于Office系列文件文字内容的提取 本文主要通过接口的方式获取Office文件和PDF、OFD文件的文字内容。适用于需要获取Word、OFD、PDF、PPT等文件内容的提取实现。例如在线文字统计以及论文文字内容的提取。 一、提取Word及WPS文档的文字内容。 支持以下文件格式: …...
