力扣DAY63-67 | 热100 | 二分:搜索插入位置、搜索二维矩阵、排序数组查找元素、搜索旋转排序数组、搜索最小值
前言
简单、中等 √ 二分法思路很简单,但是判断边界太麻烦了!难道真的要去背模板吗
搜索插入位置
我的题解
循环条件左不超过右,目标大于中间值(向下取整)时,左=中+1,小于,右=中-1,否则直接返回mid,出循环后返回left。
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;int mid;while (left <= right){mid = ((right - left) >> 1) + left;if (target > nums[mid]){left = mid + 1;}else if (target < nums[mid]){right = mid - 1;}else{return mid;} }return left;}
};官方题解
官解的条件:目标大于中间值时left也++,最后返回left
心得
标准的就是简洁优雅!不对称的原因在于求mid也是不对称的:向下取整。
搜索二维矩阵
此题之前做过一模一样的,不赘述。
在排序数组中查找元素的第一个和最后一个位置
我的题解
用二分法查找到这个元素之后,向两边扩展直到不等于目标值为止。
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if (nums.empty())return{-1, -1};int n = nums.size();int left = 0;int right = n-1;while (left < right){int mid = (left + right)/2;if (target > nums[mid])left = mid + 1;else if (target < nums[mid])right = mid - 1;else{left = mid;break;}}if (left >= n || target != nums[left])return{-1, -1};right = left;while (left > 0 && nums[left-1] == target){left--;}while (right < (n-1) && nums[right+1] == target){right++;}return {left, right};}
};官方题解
直观的思路肯定是从前往后遍历一遍。用两个变量记录第一次和最后一次遇见 target 的下标,但这个方法的时间复杂度为 O(n),没有利用到数组升序排列的条件。
由于数组已经排序,因此整个数组是单调递增的,我们可以利用二分法来加速查找的过程。
考虑 target 开始和结束位置,其实我们要找的就是数组中「第一个等于 target 的位置」(记为 leftIdx)和「第一个大于 target 的位置减一」(记为 rightIdx)。
二分查找中,寻找 leftIdx 即为在数组中寻找第一个大于等于 target 的下标,寻找 rightIdx 即为在数组中寻找第一个大于 target 的下标,然后将下标减一。两者的判断条件不同,为了代码的复用,我们定义 binarySearch(nums, target, lower) 表示在 nums 数组中二分查找 target 的位置,如果 lower 为 true,则查找第一个大于等于 target 的下标,否则查找第一个大于 target 的下标。
最后,因为 target 可能不存在数组中,因此我们需要重新校验我们得到的两个下标 leftIdx 和 rightIdx,看是否符合条件,如果符合条件就返回 [leftIdx,rightIdx],不符合就返回 [−1,−1]
class Solution {
public:int binarySearch(vector<int>& nums, int target, bool lower) {int left = 0, right = (int)nums.size() - 1, ans = (int)nums.size();while (left <= right) {int mid = (left + right) / 2;if (nums[mid] > target || (lower && nums[mid] >= target)) {right = mid - 1;ans = mid;} else {left = mid + 1;}}return ans;}vector<int> searchRange(vector<int>& nums, int target) {int leftIdx = binarySearch(nums, target, true);int rightIdx = binarySearch(nums, target, false) - 1;if (leftIdx <= rightIdx && rightIdx < nums.size() && nums[leftIdx] == target && nums[rightIdx] == target) {return vector<int>{leftIdx, rightIdx};} return vector<int>{-1, -1};}
};
心得
原来我的题解在极端情况下不是log(n),例如整个数组都是target的情况下。所以还是官解好一点(其实也不一定,n不一定比2log(n)大)。anyway其实官解先定义一个函数找目标值,不同的是多定义了一个bool变量控制right指针的移动/等号条件,当bool为true时,找的是第一个大于等于target的位置,false时找的时第一个大于target的位置。仔细想还挺有意思!
搜索旋转排序数组
我的题解
事实上我是先写了寻找最小值再写这题。找到了最小值坐标后相当于找到了两段有序数组,分别对两段有序数组进行二分查找即可。
class Solution {
public:int findtarget(vector<int> nums, int left, int right, int target){int mid;while(left < right){mid = (right - left)/2 + left;if (target > nums[mid]){left = mid + 1;}else if (target < nums[mid]){right = mid - 1;}else{left = mid;break;}}if(nums[left] == target)return left;elsereturn -1;}int search(vector<int>& nums, int target) {int n = nums.size();int low = 0;int high = n - 1;int mid = ((high - low)>>1) + low;while (low < high){mid = ((high - low)>>1) + low;if (nums[mid] < nums[high]){high = mid;}else if (nums[mid] > nums[high]){low = mid + 1;}else{break;}}return max (findtarget(nums, low, n-1, target), findtarget(nums, 0, low-1, target));}
};官方题解
对于有序数组,可以使用二分查找的方法查找元素。
但是这道题中,数组本身不是有序的,进行旋转后只保证了数组的局部是有序的,这还能进行二分查找吗?答案是可以的。
可以发现的是,我们将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的。拿示例来看,我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分,其中左边 [4, 5, 6] 这个部分的数组是有序的,其他也是如此。
这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的,并根据有序的那个部分确定我们该如何改变二分查找的上下界,因为我们能够根据有序的那部分判断出 target 在不在这个部分:
如果 [l, mid - 1] 是有序数组,且 target 的大小满足 [nums[l],nums[mid]),则我们应该将搜索范围缩小至 [l, mid - 1],否则在 [mid + 1, r] 中寻找。
如果 [mid, r] 是有序数组,且 target 的大小满足 (nums[mid+1],nums[r]],则我们应该将搜索范围缩小至 [mid + 1, r],否则在 [l, mid - 1] 中寻找。
class Solution {
public:int search(vector<int>& nums, int target) {int n = (int)nums.size();if (!n) {return -1;}if (n == 1) {return nums[0] == target ? 0 : -1;}int l = 0, r = n - 1;while (l <= r) {int mid = (l + r) / 2;if (nums[mid] == target) return mid;if (nums[0] <= nums[mid]) {if (nums[0] <= target && target < nums[mid]) {r = mid - 1;} else {l = mid + 1;}} else {if (nums[mid] < target && target <= nums[n - 1]) {l = mid + 1;} else {r = mid - 1;}}}return -1;}
};心得
官解的逻辑是,中点哪边是有序的,在有序的一边判断target是否在这个区间内,如果在则把一边的边界移到这个区间中,否则把两个边界都移出区间并重复上述步骤。此题重点在于通过判断target是否在有序区间内从而缩小范围。感觉有点低估二分法了,能变形好多解法啊!!
寻找旋转排序数组中的最小值
我的题解
如果左区间有序,移动右指针,如果右区间有序移动左指针,直到两个指针相遇。写得好乱...
class Solution {
public:int findMin(vector<int>& nums) {int n = nums.size();int left = 0;int right = n - 1;int mid = ((right - left)>>1) + left;int ans = nums[left];while (left < right){ans = min(ans, nums[mid]);ans = min(ans, nums[left]);if (nums[mid] < nums[left] && nums[mid] < nums[right]){right = mid - 1;mid = (mid + left - 1)/2;}else if (nums[mid] > nums[left] && nums[mid] > nums[right]){left = mid + 1;mid = (mid + right + 1)/2;}else{break;}}return min(ans, nums[right]);}
};官方题解
一个不包含重复元素的升序数组在经过旋转之后,可以得到下面可视化的折线图:
其中横轴表示数组元素的下标,纵轴表示数组元素的值。图中标出了最小值的位置,是我们需要查找的目标。
我们考虑数组中的最后一个元素 x:在最小值右侧的元素(不包括最后一个元素本身),它们的值一定都严格小于 x;而在最小值左侧的元素,它们的值一定都严格大于 x。因此,我们可以根据这一条性质,通过二分查找的方法找出最小值。
在二分查找的每一步中,左边界为 low,右边界为 high,区间的中点为 pivot,最小值就在该区间内。我们将中轴元素 nums[pivot] 与右边界元素 nums[high] 进行比较,可能会有以下的三种情况:
第一种情况是 nums[pivot]<nums[high]。如下图所示,这说明 nums[pivot] 是最小值右侧的元素,因此我们可以忽略二分查找区间的右半部分。
第二种情况是 nums[pivot]>nums[high]。如下图所示,这说明 nums[pivot] 是最小值左侧的元素,因此我们可以忽略二分查找区间的左半部分。
由于数组不包含重复元素,并且只要当前的区间长度不为 1,pivot 就不会与 high 重合;而如果当前的区间长度为 1,这说明我们已经可以结束二分查找了。因此不会存在 nums[pivot]=nums[high] 的情况。
当二分查找结束时,我们就得到了最小值所在的位置。
class Solution {
public:int findMin(vector<int>& nums) {int low = 0;int high = nums.size() - 1;while (low < high) {int pivot = low + (high - low) / 2;if (nums[pivot] < nums[high]) {high = pivot;}else {low = pivot + 1;}}return nums[low];}
};心得
自己写得真是乱七八糟,官解就优雅很多。当右边比较大的时候说明右区间有序,最小值在左区间,收窄右区间(中间值有可能最小,故不越界),否则说明右区间无序,最小值在右区间,收窄左区间(中间值不可能为最小,故越界)。另外由于中间值是向下取整且循环条件是小于,故不可能等于右指针,所以无需考虑中间值=右边的情况。
二分的思想在于每次淘汰一半!!
相关文章:

力扣DAY63-67 | 热100 | 二分:搜索插入位置、搜索二维矩阵、排序数组查找元素、搜索旋转排序数组、搜索最小值
前言 简单、中等 √ 二分法思路很简单,但是判断边界太麻烦了!难道真的要去背模板吗 搜索插入位置 我的题解 循环条件左不超过右,目标大于中间值(向下取整)时,左中1,小于,右中-1&…...

基于Python爬虫的豆瓣电影信息爬取(可以根据选择电影编号得到需要的电影信息)
# 豆瓣电影信息爬虫(展示效果如下图所示:) 这是一个功能强大的豆瓣电影信息爬虫程序,可以获取豆瓣电影 Top 250 的详细信息。 ## 功能特点 - 自动爬取豆瓣电影 Top 250 的所有电影信息 - 支持分页获取,每页 25 部电影,共 10 页 - 获取每部电影的详细信息,包括: - 标题…...

程序员思维体操:TDD修炼手册
程序员思维体操:TDD修炼手册 ——从"先写代码"到"测试先行"的认知革命 一、重新认识TDD:不仅仅是写测试 什么是TDD(测试驱动开发) TDD其实很简单,不要看名字很高级复杂,传统开发是直…...

PHP异常处理__RuntimeException运行时错误
以下是对 PHP 中 RuntimeException 的详细解释: 一、RuntimeException 概述 RuntimeException 是 PHP 内置的异常类,它继承自 Exception 类。它通常用于表示在程序运行时发生的异常情况,这些异常情况通常是在程序正常执行过程中出现的错误&…...

从性能到安全:大型网站系统架构演化的 13 个核心维度
大型网站系统架构的演化是一个复杂的过程,涉及到多个维度的技术内容,从关键维度进行详细分析: 1.性能维度 缓存技术:包括浏览器缓存、CDN(内容分发网络)缓存、服务器端缓存(如 Memcached、Red…...

基于PaddleOCR对图片中的excel进行识别并转换成word优化(二)
0、原图 一、优化地方 计算行的时候,采用概率分布去统计差值概率比较大的即为所要的值。 def find_common_difference(array):"""判断数组中每个元素的差值是否相等,并返回该差值:param array: 二维数组,其中每个元素是一个…...
)
spring Ai---向量知识库(二)
RAG:检索增强,结合了检索和生成两种技术;用于提升生成模型的效果。 1.信息检索(R) :系统从一个大型文档库中检索出与查询最相关的文档片段。这一步的目标是找到那些可能包含答案或相关信息的文档。 2.生成增强…...

Nvidia显卡架构演进
1 简介 显示卡(英语:Display Card)简称显卡,也称图形卡(Graphics Card),是个人电脑上以图形处理器(GPU)为核心的扩展卡,用途是提供中央处理器以外的微处理器帮…...

rollup使用讲解
rollup 总结 什么是 rollup? rollup 是一个 JavaScript 模块打包器,在功能上要完成的事和 webpack 性质一样,就是将小块代码编译成大块复杂的代码,例如 library 或应用程序。在平时开发应用程序时,我们基本上选择用 webpack,相比之下,rollup.js 更多是用于 library 打…...

USO服务器操作系统手动升级GCC 12.2.0版本
1. 从 GNU 官方 FTP 服务器下载 GCC 12.2.0 的源码包,并解压进入源码目录。 wget https://ftp.gnu.org/gnu/gcc/gcc-12.2.0/gcc-12.2.0.tar.gz tar -zxvf gcc-12.2.0.tar.gz cd gcc-12.2.0 2. 运行脚本下载并配置 GCC 编译所需的依赖库。此步骤会自动下载如 GMP…...

STM32F407使用ESP8266实现阿里云OTA(上)
文章目录 前言一、阿里云OTA二、命令调试1.升级包上传2.OTA订阅和上报的主题3.命令调试4.具体效果三、所用到的工具和材料前言 在经过前面对ESP8266、SD卡、FLASH的了解之后,终于要进入我们的正题了,就是使用STM32和ESP8266实现阿里云的OTA。这一功能并不复杂,只是需要主要…...

玩转Docker | 使用Docker部署DashMachine个人书签工具
玩转Docker | 使用Docker部署DashMachine个人书签工具 前言一、DashMachine介绍DashMachine简介DashMachine使用场景二、系统要求环境要求环境检查Docker版本检查检查操作系统版本三、部署DashMachine服务下载镜像创建容器创建容器检查容器状态检查服务端口安全设置四、访问Das…...

测试基础笔记第九天
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、数据类型和约束1.数据类型2.约束3.主键4.不为空5.唯一6.默认值 二、数据库操作1.创建数据库2.使用数据库3.修改数据库4.删除数据库和查看所有数据库5.重点&…...

使用n8n构建自动化工作流:从数据库查询到邮件通知的使用指南
n8n是一款强大的开源工作流自动化工具,可以帮助你将各种服务和应用程序连接起来,创建复杂的自动化流程。下面我将详细介绍一个实用的n8n用例:从MySQL数据库查询数据并发送邮件通知,包括使用场景、搭建步骤和节点部署方法。 使用场…...

Python爬虫与代理IP:高效抓取数据的实战指南
目录 一、基础概念解析 1.1 爬虫的工作原理 1.2 代理IP的作用 二、环境搭建与工具选择 2.1 Python库准备 2.2 代理IP选择技巧 三、实战步骤分解 3.1 基础版:单线程免费代理 3.2 进阶版:多线程付费代理池 3.3 终极版:Scrapy框架自动…...
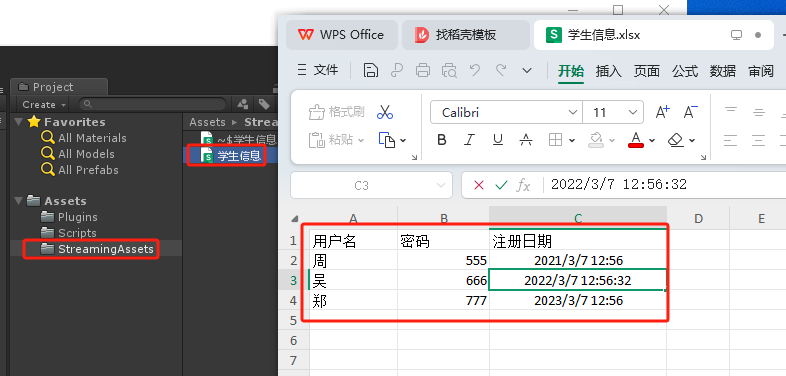
Unity 将Excel表格中的数据导入到Mysql数据表中
1.Mysql数据表users如下: 2.即将导入的Excel表格如下: 3.代码如下: using System; using System.Data; using System.IO; using Excel; using MySql.Data.MySqlClient; using UnityEngine; using UnityEditor;public class ImportExcel {// …...

JavsScript 原型链
解决构造函数浪费内存的问题 每一个构造函数都有一个属性prototype属性,指向一个原型对象 原型是构造函数的一个属性 prototype 给数组类型扩展 正常代码: prototype中的this指向为调用对象 所以 基本关系:构造函数产生两个部分&…...

MySQL 索引:深度解析与高效使用
MySQL 索引:深度解析与高效使用 引言 MySQL 是一种广泛使用的开源关系型数据库管理系统,其强大的功能和性能使其成为众多应用程序的首选数据库。在 MySQL 中,索引是提高查询效率的关键因素之一。本文将深入探讨 MySQL 索引的概念、类型、创建、优化以及注意事项,帮助您更…...

消息中间件RabbitMQ02:账号的注册、点对点推送信息
一、默认用户登录和账号注册 1.登录 安装好了RMQ之后,我们可以访问如下地址: RabbitMQ Management 输入默认的管理员密码,4.1.0的管理员账号和密码是: guest guest 2.添加账号 consumer consumer 添加成功后: 角色…...

大语言模型的评估指标
目录 一、混淆矩阵 1. 混淆矩阵的结构(二分类为例) 2.从混淆矩阵衍生的核心指标 3.多分类任务的扩展 4. 混淆矩阵的实战应用 二、分类任务核心指标 1. Accuracy(准确率) 2. Precision(精确率) 3. …...

Python 设计模式:模板模式
1. 什么是模板模式? 模板模式是一种行为设计模式,它定义了一个操作的算法的骨架,而将一些步骤延迟到子类中。模板模式允许子类在不改变算法结构的情况下,重新定义算法的某些特定步骤。 模板模式的核心思想是将算法的固定部分提取…...

HSTL详解
一、HSTL的基本定义 HSTL(High-Speed Transceiver Logic) 是一种针对高速数字电路设计的差分信号接口标准,主要用于高带宽、低功耗场景(如FPGA、ASIC、高速存储器接口)。其核心特性包括: 差分信号传输&…...
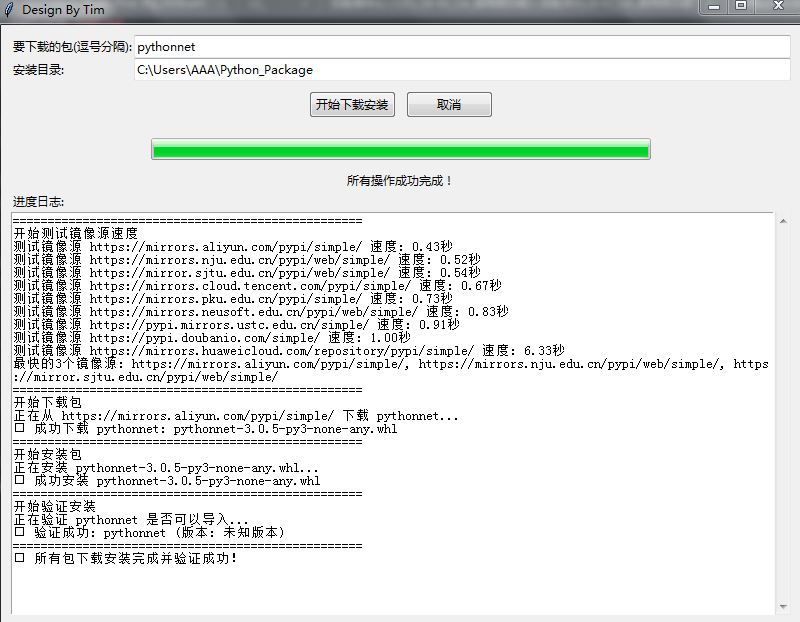
好用————python 库 下载 ,整合在一个小程序 UIUIUI
上图~ import os import time import threading import requests import subprocess import importlib import tkinter as tk from tkinter import ttk, messagebox, scrolledtext from concurrent.futures import ThreadPoolExecutor, as_completed from urllib.parse im…...

OpenVINO教程(五):实现YOLOv11+OpenVINO实时视频目标检测
目录 实现讲解效果展示完整代码 本文作为上篇博客的延续,在之前实现了图片推理的基础上,进一步介绍如何进行视频推理。 实现讲解 首先,我们需要对之前的 predict_and_show_image 函数进行拆分,将图像显示与推理器(pre…...

CentOS的安装以及网络配置
CentOS的下载 在学习docker之前,我们需要知道的就是docker是运行在Linux内核之上的,所以我们需要Linux环境的操作系统,当然了你也可以选择安装ubuntu等操作系统,如果你不想在本机安装的话还可以考虑买阿里或者华为的云服务器&…...
)
【初级】前端开发工程师面试100题(一)
本题库共计包含100题,考察html,css,js,以及react,vue,webpack等基础知识掌握情况。 HTML基础篇 说说你对HTML语义化的理解? 语义化就是用合适的标签表达合适的内容,比如<header&…...

eplan许可证与防火墙安全软件冲突
在使用EPLAN电气设计软件时,有时会遇到许可证与防火墙或安全软件之间的冲突。这种冲突可能导致许可证无法激活或软件无法正常运行,给用户带来诸多不便。本文将为您解析EPLAN许可证与防火墙/安全软件冲突的原因,并提供解决方案,帮助…...

「Java EE开发指南」用MyEclipse开发EJB 3无状态会话Bean(二)
本教程介绍在MyEclipse中开发EJB 3无状态会话bean,由于JPA实体和EJB 3实体非常相似,因此本教程不涉及EJB 3实体Bean的开发。在本教程中,您将学习如何: 创建EJB 3项目创建无状态会话bean部署并测试bean 在上文中(点击…...

Stable Diffusion秋叶整合包V4独立版Python本地API连接指南
秋叶整合包V4独立版Python本地API连接指南 秋叶整合的Stable Diffusion V4独立版支持通过Python调用本地API实现自动化图像生成。以下是具体操作流程及注意事项: 一、启用API服务 启动器配置 • 在秋叶启动器的 高级选项 中添加以下参数: --api --liste…...

小程序 GET 接口两种传值方式
前言 一般 GET 接口只有两种URL 参数和路径参数 一:URL 参数(推荐方式) 你希望请求: https://serve.zimeinew.com/wx/products/info?id5124接口应该写成这样,用 req.query.id 取 ?id5124: app.get(&…...
