位运算题目:解码异或后的排列
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:解码异或后的排列
出处:1734. 解码异或后的排列
难度
6 级
题目描述
要求
有一个整数数组 perm \texttt{perm} perm,是前 n \texttt{n} n 个正整数的排列,且 n \texttt{n} n 是奇数。
它被加密成另一个长度为 n − 1 \texttt{n} - \texttt{1} n−1 的整数数组 encoded \texttt{encoded} encoded,满足 encoded[i] = perm[i] ⊕ perm[i + 1] \texttt{encoded[i] = perm[i]} \oplus \texttt{perm[i + 1]} encoded[i] = perm[i]⊕perm[i + 1]。例如,如果 perm = [1,3,2] \texttt{perm = [1,3,2]} perm = [1,3,2],那么 encoded = [2,1] \texttt{encoded = [2,1]} encoded = [2,1]。
给定 encoded \texttt{encoded} encoded 数组,返回原始数组 perm \texttt{perm} perm。题目保证答案存在且唯一。
示例
示例 1:
输入: encoded = [3,1] \texttt{encoded = [3,1]} encoded = [3,1]
输出: [1,2,3] \texttt{[1,2,3]} [1,2,3]
解释:如果 perm = [1,2,3] \texttt{perm = [1,2,3]} perm = [1,2,3],那么 encoded = [1 ⊕ 2,2 ⊕ 3] = [3,1] \texttt{encoded = [1} \oplus \texttt{2,2} \oplus \texttt{3] = [3,1]} encoded = [1⊕2,2⊕3] = [3,1]。
示例 2:
输入: encoded = [6,5,4,6] \texttt{encoded = [6,5,4,6]} encoded = [6,5,4,6]
输出: [2,4,1,5,3] \texttt{[2,4,1,5,3]} [2,4,1,5,3]
数据范围
- 3 ≤ n < 10 5 \texttt{3} \le \texttt{n} < \texttt{10}^\texttt{5} 3≤n<105
- n \texttt{n} n 是奇数
- encoded.length = n − 1 \texttt{encoded.length} = \texttt{n} - \texttt{1} encoded.length=n−1
解法
思路和算法
对于 0 ≤ i < n − 1 0 \le i < n - 1 0≤i<n−1 有 encoded [ i ] = perm [ i ] ⊕ perm [ i + 1 ] \textit{encoded}[i] = \textit{perm}[i] \oplus \textit{perm}[i + 1] encoded[i]=perm[i]⊕perm[i+1],利用按位异或的性质可以得到 encoded [ i ] ⊕ perm [ i ] = perm [ i + 1 ] ⊕ perm [ i ] ⊕ perm [ i ] = perm [ i + 1 ] \textit{encoded}[i] \oplus \textit{perm}[i] = \textit{perm}[i + 1] \oplus \textit{perm}[i] \oplus \textit{perm}[i] = \textit{perm}[i + 1] encoded[i]⊕perm[i]=perm[i+1]⊕perm[i]⊕perm[i]=perm[i+1]。因此对于 1 ≤ i < n 1 \le i < n 1≤i<n 有 perm [ i ] = encoded [ i − 1 ] ⊕ perm [ i − 1 ] \textit{perm}[i] = \textit{encoded}[i - 1] \oplus \textit{perm}[i - 1] perm[i]=encoded[i−1]⊕perm[i−1]。如果可以知道 perm [ 0 ] \textit{perm}[0] perm[0] 的值,则可以解码得到完整的原始数组 perm \textit{perm} perm。
由于数组 perm \textit{perm} perm 的长度 n n n 是奇数,因此除了 perm [ 0 ] \textit{perm}[0] perm[0] 以外的剩余元素个数 n − 1 n - 1 n−1 是偶数,数组 encoded \textit{encoded} encoded 的长度 n − 1 n - 1 n−1 是偶数。可以在数组 encoded \textit{encoded} encoded 中寻找 n − 1 2 \dfrac{n - 1}{2} 2n−1 个元素,使得这些元素的异或结果为 perm [ 1 ] \textit{perm}[1] perm[1] 到 perm [ n − 1 ] \textit{perm}[n - 1] perm[n−1] 的异或结果。
由于 encoded [ i ] = perm [ i ] ⊕ perm [ i + 1 ] \textit{encoded}[i] = \textit{perm}[i] \oplus \textit{perm}[i + 1] encoded[i]=perm[i]⊕perm[i+1],因此计算 encoded \textit{encoded} encoded 的所有奇数下标处的元素的异或结果,记为 oddXor \textit{oddXor} oddXor,则该异或结果为 encoded \textit{encoded} encoded 的 n − 1 2 \dfrac{n - 1}{2} 2n−1 个元素的异或结果,等于 perm [ 1 ] \textit{perm}[1] perm[1] 到 perm [ n − 1 ] \textit{perm}[n - 1] perm[n−1] 的异或结果。
用 totalXor \textit{totalXor} totalXor 表示 1 1 1 到 n n n 的所有整数的异或结果,则 totalXor = oddXor ⊕ perm [ 0 ] \textit{totalXor} = \textit{oddXor} \oplus \textit{perm}[0] totalXor=oddXor⊕perm[0],利用按位异或的性质可以得到 totalXor ⊕ oddXor = oddXor ⊕ oddXor ⊕ perm [ 0 ] = perm [ 0 ] \textit{totalXor} \oplus \textit{oddXor} = \textit{oddXor} \oplus \textit{oddXor} \oplus \textit{perm}[0] = \textit{perm}[0] totalXor⊕oddXor=oddXor⊕oddXor⊕perm[0]=perm[0],即 perm [ 0 ] \textit{perm}[0] perm[0] 的值等于 totalXor \textit{totalXor} totalXor 和 oddXor \textit{oddXor} oddXor 的异或结果。
得到 perm [ 0 ] \textit{perm}[0] perm[0] 的值之后,从 i = 1 i = 1 i=1 到 i = n − 1 i = n - 1 i=n−1 依次计算 perm [ i ] \textit{perm}[i] perm[i] 的值,即可得到原数组 perm \textit{perm} perm,且原数组的结果唯一。
代码
class Solution {public int[] decode(int[] encoded) {int n = encoded.length + 1;int[] perm = new int[n];int totalXor = 0;for (int i = 1; i <= n; i++) {totalXor ^= i;}int oddXor = 0;for (int i = 1; i < n; i += 2) {oddXor ^= encoded[i];}perm[0] = totalXor ^ oddXor;for (int i = 1; i < n; i++) {perm[i] = encoded[i - 1] ^ perm[i - 1];}return perm;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组 perm \textit{perm} perm 的长度。需要遍历 1 1 1 到 n n n 的所有整数计算总异或值,然后遍历长度为 n − 1 n - 1 n−1 的数组 encoded \textit{encoded} encoded 两次得到原始数组 perm \textit{perm} perm。
-
空间复杂度: O ( 1 ) O(1) O(1)。注意返回值不计入空间复杂度。
相关文章:

位运算题目:解码异或后的排列
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:解码异或后的排列 出处:1734. 解码异或后的排列 难度 6 级 题目描述 要求 有一个整数数组 perm \texttt{perm} perm,是前…...

【Spring Boot】深入解析:#{} 和 ${}
1.#{} 和 ${}的使用 1.1数据准备 1.1.1.MySQL数据准备 (1)创建数据库: CREATE DATABASE mybatis_study DEFAULT CHARACTER SET utf8mb4;(2)使用数据库 -- 使⽤数据数据 USE mybatis_study;(3ÿ…...

linux:启动后,ubuntu屏幕变成红色了
屏幕启动后变成 红色背景 通常说明 显卡驱动出了问题,或者是 图形界面加载失败 使用了 fallback 模式。这种现象在 NVIDIA 驱动安装失败或显卡与驱动不兼容时常见。 🎯 先给你几个快速修复选项 ✅ 1. 进入 TTY 命令行界面 按下:Ctrl Alt …...

从实验室到产业端:解码 GPU 服务器的八大核心应用场景
一、深度学习与人工智能的基石 在深度学习领域,GPU 服务器的并行计算架构成为训练大规模模型的核心引擎 —— 传统 CPU 集群训练千亿参数模型需数月,而基于某国际知名芯片厂商 H100 的 GPU 服务器可将周期缩短至数周,国内科技巨头 910B 芯…...

java—12 kafka
目录 一、消息队列的优缺点 二、常用MQ 1. Kafka 2. RocketMQ 3. RabbitMQ 4. ActiveMQ 5. ZeroMQ 6. MQ选型对比 适用场景——从公司基础建设力量角度出发 适用场景——从业务场景角度出发 四、基本概念和操作 1. kafka常用术语 2. kafka常用指令 3. 单播消息&a…...

YOLOv8 涨点新方案:SlideLoss FocalLoss 优化,小目标检测效果炸裂!
YOLOv8优化秘籍:用SlideLoss和FocalLoss提升小目标检测精度(附代码实战) 📌 核心问题:YOLOv8在检测小物体时效果不够好? YOLOv8虽然是强大的目标检测模型,但在处理小物体或类别不平…...

数据库-数据类型、约束 和 DQL语言
标题目录 数据类型数字类型INT 型BIGINT 型DOUBLE 类型 字符类型定长字符串变长字符串 日期类型 约束主键约束非空约束唯一性约束检查约束外键约束 DQL 语言WHERE 子句连接多个条件IN (列表)NOT IN (列表)BETWEEN...AND...DISTINCT多字段去重 模糊查询NULL 值判断排序ÿ…...

verilog和system verilog常用数据类型以及常量汇总
int和unsigned 在 Verilog-2001 中,没有 int 和 unsigned 这样的数据类型。这些关键字是 SystemVerilog 的特性,而不是 Verilog-2001 的一部分。 Verilog-2001 的数据类型 在 Verilog-2001 中,支持的数据类型主要包括以下几种: …...

Dify升级-linux环境下使用zip离线安装方式部署升级
Dify安装时Linux服务器到github网络不好,git clone拉去不下来代码。使用本地windows电脑下载zip包形式上传进行了安装。但是随着dfiy版本升级,本地使用最新版本的,也需要进行下升级。参考升级指导以及自己环境情况,升级步骤如下。…...
)
容器修仙传 我的灵根是Pod 第9章 时空禁术(Job与CronJob)
第三卷:上古遗迹元婴篇 第9章 时空禁术(Job与CronJob) 极北冰渊深处,万丈冰层下封印着上古禁术「轮回溯光阵」。 林衍的混沌灵根突然结出冰霜——这不是寒冷所致,而是阵法中逸散的时空乱流。冰壁上刻满血色符文&…...
)
Web3.0的认知补充(去中心化)
涉及开发技术: Vue Web3.js Solidity 基本认知 Web3.0含义: 新一代互联网思想:去中心化及用户为中心的互联网 数据:可读可写可授权 核心技术:区块链、NFT 应用:互联网上应用 NFT &…...

【Python网络爬虫实战指南】从数据采集到反反爬策略
目录 前言技术背景与价值当前技术痛点解决方案概述目标读者说明 一、技术原理剖析核心概念图解核心作用讲解关键技术模块说明技术选型对比 二、实战演示环境配置要求核心代码实现案例1:静态页面抓取(电商价格)案例2:动态页面抓取&…...

Atlas 800I A2 离线部署 DeepSeek-R1-Distill-Llama-70B
一、环境信息 1.1、硬件信息 Atlas 800I A2 1.2、环境信息 注意:这里驱动固件最好用商业版,我这里用的社区版有点小问题 操作系统:openEuler 22.03 LTS NPU驱动:Ascend-hdk-910b-npu-driver_24.1.rc3_linux-aarch64.run NPU固…...

基于SpringBoot+Vue的影视系统(源码+lw+部署文档+讲解),源码可白嫖!
摘要 时代在飞速进步,每个行业都在努力发展现在先进技术,通过这些先进的技术来提高自己的水平和优势,影视推荐系统当然不能排除在外。影视系统是在实际应用和软件工程的开发原理之上,运用Java语言以及Spring Boot、VUE框架进行开…...

搭建Stable Diffusion图像生成系统实现通过网址访问(Ngrok+Flask实现项目系统公网测试,轻量易部署)
目录 前言 背景与需求 🎯 需求分析 核心功能 网络优化 方案确认 1. 安装 Flask 和 Ngrok 2. 构建 Flask 应用 3. 使用 Ngrok 实现内网穿透 4. 测试图像生成接口 技术栈 实现流程 优化目标 实现细节 1. 迁移到Flask 2. 持久化提示词 3. 图像下载功能 …...

Java 21 的“无类主”特性:简化编程的第一步
在Java编程中,编写一个简单的“Hello, World!”程序通常需要以下代码: public class HelloWorld {public static void main(String[] args) {System.out.println("Hello, World!");} }这种结构包含了许多对初学者来说难以理解的概念ÿ…...

AI | 最近比较火的几个生成式对话 AI
关注:CodingTechWork 引言 生成式对话 AI 正在迅速改变我们与机器交互的方式,从智能助手到内容创作,其应用范围广泛且深远。本文将深入探讨几款当前热门的生成式对话 AI 模型,包括 Kimi、DeepSeek、ChatGPT、文心一言、通义千问和…...
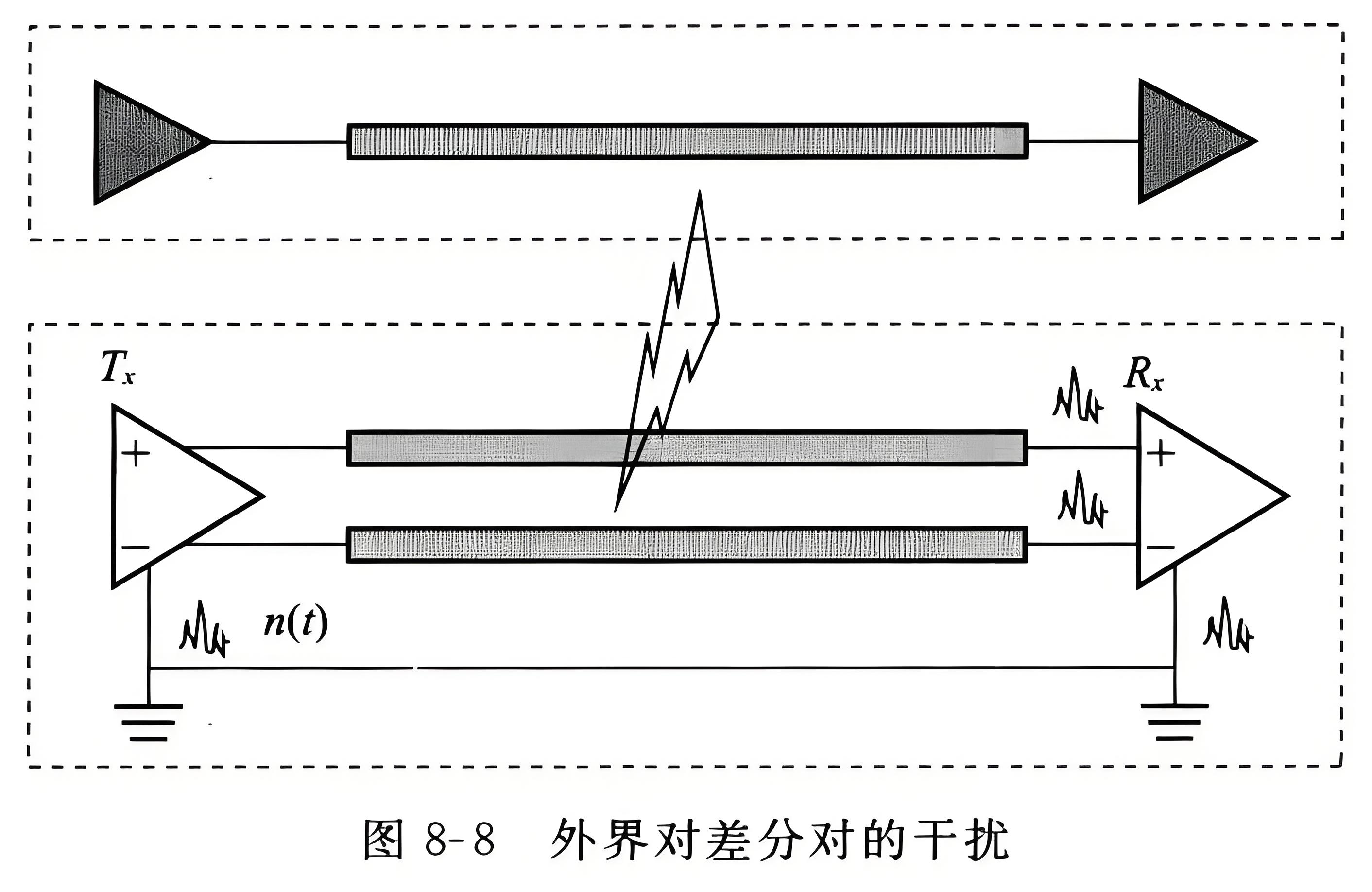
差分信号抗噪声原理:
差分信号抗噪声原理: 差分信号除了能很好地解决发送和接收参考点电位不同的问题外,差分信号的另一个重要优势就是在一定条件下其抗干扰能力比单端信号更强。对于单端信号传输,外界对它的干扰噪声直接叠加在信号上,接收端直接检测输…...

6 种AI实用的方法,快速修复模糊照片
照片是我们记录生活的重要方式。但有时,由于各种原因,照片会变得模糊,无法展现出我们想要的效果。幸运的是,随着人工智能(AI)技术的发展,现在有多种方法可以利用 AI 修复模糊照片,让…...

JavaScript 的“积木”:函数入门与实践
引言:告别重复,拥抱模块化 想象一下,你在写代码时发现,有几段逻辑几乎一模一样,需要在不同的地方反复使用。你是选择每次都复制粘贴,还是希望能像搭积木一样,把这段逻辑封装起来,需…...

从入门到精通【MySQL】视图与用户权限管理
文章目录 📕1. 视图✏️1.1 视图的基本概念✏️1.2 试图的基本操作🔖1.2.1 创建视图🔖1.2.2 使用视图🔖1.2.3 修改数据🔖1.2.4 删除视图 ✏️1.3 视图的优点 📕2. 用户与权限管理✏️2.1 用户🔖…...

C++中的next_permutation全排列函数
目录 什么是全排列用法实现原理自定义比较函数 注意事项相关题目1.AB Problem2.P1088 火星人 什么是全排列 全排列是指从一组元素中按照一定顺序(按字典序排列)取出所有元素进行排列的所有可能情况。 例如,对于集合{1,2,3},它的全排列包括&a…...

修改el-select背景颜色
修改el-select背景颜色 /* 修改el-select样式--直接覆盖默认样式(推荐) */ ::v-deep .el-select .el-input__inner {background-color: #1d2b72 !important; /* 修改输入框背景色 */color: #fff; } ::v-deep .el-select .el-input__wrapper {background-…...

dockercompose文件仓库
mysql version: 3 # 使用docker-compose的版本,根据需要可以调整# 创建数据目录 # mkdir -p /home/docker/mysql/mysql_data # mkdir -p /home/docker/mysql/mysql_logs # 给予适当的权限(确保MySQL容器可以读写这些目录) # chmod 777 /ho…...

【C++入门:类和对象】[3]
C入门:类和对象 拷贝构造(拷贝初始化) 拷贝构造是构造函数的重载 class Date { public:Date(int year1,int month1,int day1) { _yearyear; _monthmonth; _dayday; } Date(const Date& d)//(拷贝构造,把d1传参给d)引用传参不改变使用const //注意使用&,不然会无穷递…...

【mdlib】0 全面介绍 mdlib - Rust 实现的 Markdown 工具集
mdlib 是由开发者 bahdotsh 创建的一个多功能 Markdown 工具集合,包含两个主要组件:一个轻量级 Markdown 解析库和一个功能完善的个人 Wiki 系统。该项目完全采用 Rust 实现,兼具高性能与跨平台特性。 核心组件 Markdown 解析库 特性&#…...

今日CSS学习浮动->定位
------------------------------------------------------------------------------------------------------- CSS的浮动 float 属性用于创建浮动框,将其移动到一边,直到左边缘或右边缘触及包含块或另一个浮动框的边缘。 float 属性定义元素在哪个方向浮…...

如何实现Spring Boot应用程序的安全性:全面指南
在现代 Web 开发中,安全性是 Spring Boot 应用程序的核心需求,尤其是在微服务、云原生和公开 API 场景中。Spring Boot 结合 Spring Security 提供了一套强大的工具,用于保护应用程序免受常见威胁,如未经授权的访问、数据泄露、跨…...

YOLOv8融合CPA-Enhancer【提高恶略天气的退化图像检测】
1.CPA介绍 CPA-Enhancer通过链式思考提示机制实现了对未知退化条件下图像的自适应增强,显著提升了物体检测性能。其插件式设计便于集成到现有检测框架中,并在物体检测及其他视觉任务中设立了新的性能标准,展现了广泛的应用潜力。 关于CPA-E…...
Python 项目环境配置与 Vanna 安装避坑指南 (PyCharm + venv)
在进行 Python 项目开发时,一个干净、隔离且配置正确的开发环境至关重要。尤其是在使用像 PyCharm 这样的集成开发环境 (IDE) 时,正确理解和配置虚拟环境 (Virtual Environment) 是避免许多常见问题的关键。本文结合之前安装 Vanna 库时遇到的问题&#…...
