青少年编程与数学 02-018 C++数据结构与算法 07课题、堆
青少年编程与数学 02-018 C++数据结构与算法 07课题、堆
- 一、堆
- 1. 定义
- 2. 堆的存储方式
- 3. 堆的常见操作
- 4. 堆的应用
- 二、最大堆的实现
- 1. 堆的存储
- 2. 基本操作
- 3. C++代码实现
- 4. 代码说明
- 5. 示例输出
- 三、最小堆的实现
- 四、建堆操作
- 1. 建堆操作的原理
- 2. 为什么从最后一个非叶子节点开始?
- 3. 建堆操作的步骤
- 4. 代码实现
- 5. 代码说明
- 6. 示例输出
- 7. 时间复杂度分析
- 8. 总结
- 五、堆的应用
- 1. 优先队列(Priority Queue)
- 应用场景:
- 2. 堆排序(Heap Sort)
- 应用场景:
- 3. 数据压缩
- 应用场景:
- 4. 中位数查找
- 应用场景:
- 5. K 个最小(或最大)元素
- 应用场景:
- 6. 图算法
- 应用场景:
- 7. 资源管理
- 应用场景:
- 8. 游戏开发
- 9. 分布式系统
- 应用场景:
- 总结
课题摘要:
在数据结构中,堆(Heap)是一种特殊的完全二叉树。
堆首先是一个完全二叉树,即除了最后一层外,每一层都被完全填满,并且所有节点都尽可能地向左对齐。
一、堆
在数据结构中,堆(Heap)是一种特殊的完全二叉树,具有以下特点:
1. 定义
- 完全二叉树:堆首先是一个完全二叉树,即除了最后一层外,每一层都被完全填满,并且所有节点都尽可能地向左对齐。
- 堆序性质:堆的节点值必须满足特定的顺序关系,分为两种类型:
- 最大堆(大顶堆):每个父节点的值都大于或等于其子节点的值。在最大堆中,根节点是所有节点中值最大的。
- 最小堆(小顶堆):每个父节点的值都小于或等于其子节点的值。在最小堆中,根节点是所有节点中值最小的。
2. 堆的存储方式
堆通常使用数组来存储,而不是像普通二叉树那样使用指针。对于数组中的第i个元素,其左子节点的索引为2i + 1,右子节点的索引为2i + 2,而其父节点的索引为(i - 1) / 2(向下取整)。
3. 堆的常见操作
- 插入元素:
- 将新元素添加到堆的末尾(即数组的最后一个位置)。
- 然后通过“上浮”操作(与父节点比较并交换,直到满足堆序性质)将其调整到合适的位置。
- 删除元素:
- 通常删除的是堆顶元素(最大堆中是最大值,最小堆中是最小值)。
- 将堆的最后一个元素移到堆顶,然后通过“下沉”操作(与子节点比较并交换,直到满足堆序性质)将其调整到合适的位置。
- 调整堆:当堆的某个节点的值发生变化时,需要通过上浮或下沉操作来重新调整堆,以保持堆的性质。
- 建堆:将一个无序的数组调整成一个堆。可以通过自底向上或自顶向下两种方式来实现。
4. 堆的应用
- 优先队列:堆是实现优先队列的常用数据结构。优先队列可以快速地获取优先级最高的元素(最大堆或最小堆的堆顶元素),并且能够高效地插入和删除元素。
- 堆排序:利用堆的性质可以实现一种高效的排序算法。通过建堆、不断删除堆顶元素并将其放到数组的末尾,可以实现对数组的排序。
- 数据压缩:在霍夫曼编码等数据压缩算法中,堆可以用于高效地管理编码树的构造过程。
- 资源分配:在操作系统中,堆可以用于管理资源的分配,根据资源的优先级进行调度。
总之,堆是一种非常重要的数据结构,它在很多领域都有广泛的应用,其高效的插入、删除和获取最值操作使其在处理优先级相关问题时具有很大的优势。
二、最大堆的实现
1. 堆的存储
我们使用数组来存储堆,数组的索引从0开始。对于索引为i的节点:
- 其左子节点的索引为
2 * i + 1 - 其右子节点的索引为
2 * i + 2 - 其父节点的索引为
(i - 1) / 2
2. 基本操作
- 上浮(Sift Up):用于插入新元素后调整堆。
- 下沉(Sift Down):用于删除堆顶元素后调整堆。
- 插入元素(Insert):将新元素添加到数组末尾,然后上浮。
- 删除堆顶元素(Extract Max):删除堆顶元素,将最后一个元素放到堆顶,然后下沉。
- 建堆(Heapify):将一个无序数组调整为堆。
3. C++代码实现
#include <iostream>
#include <vector>
using namespace std;class MaxHeap {
private:vector<int> heap;int parent(int i) {return (i - 1) / 2;}int leftChild(int i) {return 2 * i + 1;}int rightChild(int i) {return 2 * i + 2;}void siftUp(int i) {while (i > 0 && heap[parent(i)] < heap[i]) {swap(heap[parent(i)], heap[i]);i = parent(i);}}void siftDown(int i) {int maxIndex = i;int left = leftChild(i);if (left < heap.size() && heap[left] > heap[maxIndex]) {maxIndex = left;}int right = rightChild(i);if (right < heap.size() && heap[right] > heap[maxIndex]) {maxIndex = right;}if (i != maxIndex) {swap(heap[i], heap[maxIndex]);siftDown(maxIndex);}}public:void insert(int value) {heap.push_back(value);siftUp(heap.size() - 1);}int extractMax() {if (heap.empty()) {return -1; // 返回一个错误值,表示堆为空}int max_value = heap[0];heap[0] = heap.back();heap.pop_back();if (!heap.empty()) {siftDown(0);}return max_value;}void heapify(const vector<int>& array) {heap = array;for (int i = heap.size() / 2 - 1; i >= 0; --i) {siftDown(i);}}int getMax() {if (heap.empty()) {return -1; // 返回一个错误值,表示堆为空}return heap[0];}void printHeap() {for (int value : heap) {cout << value << " ";}cout << endl;}
};// 示例用法
int main() {MaxHeap maxHeap;maxHeap.insert(10);maxHeap.insert(20);maxHeap.insert(15);maxHeap.insert(30);maxHeap.insert(40);cout << "当前最大堆: ";maxHeap.printHeap();cout << "堆顶元素: " << maxHeap.getMax() << endl;cout << "删除堆顶元素: " << maxHeap.extractMax() << endl;cout << "删除后的最大堆: ";maxHeap.printHeap();vector<int> array = {12, 7, 1, 3, 10, 17, 19, 2, 5};maxHeap.heapify(array);cout << "建堆后的最大堆: ";maxHeap.printHeap();return 0;
}
4. 代码说明
- 初始化:
- 使用
vector<int>来存储堆。
- 使用
- 索引计算:
parent、leftChild和rightChild方法用于计算父节点和子节点的索引。
- 上浮操作:
siftUp方法用于将新插入的元素上浮到合适的位置,直到满足最大堆的性质。
- 下沉操作:
siftDown方法用于将堆顶元素下沉到合适的位置,直到满足最大堆的性质。
- 插入操作:
insert方法将新元素添加到数组末尾,然后调用siftUp进行调整。
- 删除堆顶元素:
extractMax方法删除堆顶元素,将最后一个元素移到堆顶,然后调用siftDown进行调整。
- 建堆:
heapify方法将一个无序数组调整为最大堆,从最后一个非叶子节点开始逐个调用siftDown。
- 获取堆顶元素:
getMax方法返回堆顶元素(最大值)。
- 打印堆:
printHeap方法用于打印堆的内容。
5. 示例输出
假设输入的数组为{12, 7, 1, 3, 10, 17, 19, 2, 5},运行代码后可能的输出如下:
当前最大堆: 40 30 15 10 20
堆顶元素: 40
删除堆顶元素: 40
删除后的最大堆: 30 20 15 10
建堆后的最大堆: 19 17 12 2 10 1 5 3 7
三、最小堆的实现
最小堆的实现与最大堆类似,唯一的区别在于堆序性质相反(父节点值小于或等于子节点值)。以下是实现最小堆的关键代码部分:
void siftUp(int i) {while (i > 0 && heap[parent(i)] > heap[i]) {swap(heap[parent(i)], heap[i]);i = parent(i);}
}void siftDown(int i) {int minIndex = i;int left = leftChild(i);if (left < heap.size() && heap[left] < heap[minIndex]) {minIndex = left;}int right = rightChild(i);if (right < heap.size() && heap[right] < heap[minIndex]) {minIndex = right;}if (i != minIndex) {swap(heap[i], heap[minIndex]);siftDown(minIndex);}
}
其他方法(如insert、extractMin等)与最大堆类似,只需将比较操作符从>改为<即可。
四、建堆操作
建堆操作(Heapify)是将一个无序的数组转换为一个合法的堆(最大堆或最小堆)的过程。这个操作是堆数据结构中的一个重要步骤,尤其是在实现堆排序算法时。以下是关于建堆操作的详细解释,包括其原理、步骤和代码实现。
1. 建堆操作的原理
建堆操作的目标是将一个无序数组调整为一个满足堆序性质的堆。堆序性质是指:
- 最大堆:每个父节点的值都大于或等于其子节点的值。
- 最小堆:每个父节点的值都小于或等于其子节点的值。
建堆操作的核心思想是从最后一个非叶子节点开始,逐个向下调整(Sift Down)每个节点,直到整个数组满足堆序性质。
2. 为什么从最后一个非叶子节点开始?
在完全二叉树中,最后一个非叶子节点的索引可以通过公式计算:
[ \text{last_non_leaf_index} = \left\lfloor \frac{n - 2}{2} \right\rfloor ]
其中,( n ) 是数组的长度。
从最后一个非叶子节点开始的原因是:
- 叶子节点本身已经是一个合法的堆(因为它们没有子节点)。
- 从最后一个非叶子节点开始逐个调整,可以确保在调整某个节点时,其子树已经是一个合法的堆。
3. 建堆操作的步骤
- 初始化:将无序数组存储到一个数组中。
- 找到最后一个非叶子节点:计算最后一个非叶子节点的索引。
- 逐个调整:从最后一个非叶子节点开始,逐个向下调整每个节点,直到根节点。
4. 代码实现
以下是最大堆的建堆操作的 C++ 实现:
#include <iostream>
#include <vector>
using namespace std;class MaxHeap {
private:vector<int> heap;int parent(int i) {return (i - 1) / 2;}int leftChild(int i) {return 2 * i + 1;}int rightChild(int i) {return 2 * i + 2;}void siftDown(int i) {int maxIndex = i;int left = leftChild(i);if (left < heap.size() && heap[left] > heap[maxIndex]) {maxIndex = left;}int right = rightChild(i);if (right < heap.size() && heap[right] > heap[maxIndex]) {maxIndex = right;}if (i != maxIndex) {swap(heap[i], heap[maxIndex]);siftDown(maxIndex);}}public:MaxHeap(const vector<int>& array) {heap = array;heapify();}void heapify() {int n = heap.size();int lastNonLeafIndex = (n - 2) / 2;for (int i = lastNonLeafIndex; i >= 0; --i) {siftDown(i);}}void printHeap() {for (int value : heap) {cout << value << " ";}cout << endl;}
};// 示例用法
int main() {vector<int> array = {12, 7, 1, 3, 10, 17, 19, 2, 5};MaxHeap maxHeap(array);cout << "建堆后的最大堆: ";maxHeap.printHeap();return 0;
}
5. 代码说明
- 初始化:
- 如果传入了一个数组,直接复制该数组到
heap,并调用heapify方法进行建堆。
- 如果传入了一个数组,直接复制该数组到
- 计算最后一个非叶子节点:
- 使用公式
lastNonLeafIndex = (n - 2) / 2计算最后一个非叶子节点的索引。
- 使用公式
- 逐个调整:
- 从最后一个非叶子节点开始,逐个调用
siftDown方法,将每个节点调整到合适的位置,直到整个数组满足最大堆的性质。
- 从最后一个非叶子节点开始,逐个调用
6. 示例输出
假设输入的数组为{12, 7, 1, 3, 10, 17, 19, 2, 5},运行代码后可能的输出如下:
建堆后的最大堆: 19 17 12 2 10 1 5 3 7
7. 时间复杂度分析
建堆操作的时间复杂度是(O(n))。虽然看起来有两层循环(外层循环从最后一个非叶子节点到根节点,内层循环是siftDown),但实际的时间复杂度并不是(O(n \log n))。这是因为越靠近根节点的元素,其子树越小,调整的次数也越少。经过数学分析,建堆操作的总时间复杂度为(O(n))。
8. 总结
建堆操作是将一个无序数组转换为一个合法堆的过程,通过从最后一个非叶子节点开始逐个调整节点,可以高效地完成建堆。建堆操作是堆排序算法中的关键步骤,也是堆数据结构中的一个重要操作。
五、堆的应用
堆(Heap)是一种非常灵活且高效的数据结构,广泛应用于计算机科学的各个领域。以下是堆的一些主要应用,按不同场景分类介绍:
1. 优先队列(Priority Queue)
优先队列是一种特殊的队列,其中每个元素都有一个优先级,优先级最高的元素最先被取出。堆是实现优先队列的最常用数据结构之一,因为堆能够高效地支持以下操作:
- 插入元素:将一个新元素插入到优先队列中,时间复杂度为 (O(\log n))。
- 获取最高优先级元素:快速获取优先队列中优先级最高的元素,时间复杂度为 (O(1))。
- 删除最高优先级元素:移除优先队列中优先级最高的元素,时间复杂度为 (O(\log n))。
应用场景:
- 任务调度:操作系统中,根据任务的优先级调度进程或线程。
- 事件驱动模拟:在模拟系统中,根据事件的时间顺序处理事件。
- 资源分配:根据资源的优先级分配有限的资源。
2. 堆排序(Heap Sort)
堆排序是一种高效的排序算法,利用堆的性质对数组进行排序。堆排序的基本步骤如下:
- 建堆:将无序数组转换为一个最大堆(或最小堆)。
- 排序:重复以下步骤,直到堆为空:
- 删除堆顶元素(最大值或最小值),并将其放到数组的末尾。
- 将堆的最后一个元素移到堆顶,然后调整堆以恢复堆序性质。
堆排序的时间复杂度为 (O(n \log n)),并且是一种不稳定的排序算法。
应用场景:
- 通用排序:对数组或列表进行排序,尤其是在需要原地排序(不使用额外空间)的场景中。
- 数据预处理:在数据挖掘或机器学习中,对数据进行预处理和排序。
3. 数据压缩
堆在数据压缩算法中也有重要应用,例如霍夫曼编码(Huffman Coding)。霍夫曼编码是一种基于字符频率的无损压缩算法,通过构建霍夫曼树来实现高效的编码和解码。
应用场景:
- 文件压缩:如 ZIP、GZIP 等压缩工具中,霍夫曼编码用于压缩文本文件。
- 网络传输:在传输大量数据时,使用霍夫曼编码减少数据量。
4. 中位数查找
堆可以用于高效地查找数据流中的中位数。通过维护两个堆(一个最大堆和一个最小堆),可以动态地插入新元素并快速获取中位数。
应用场景:
- 实时数据分析:在处理实时数据流时,快速计算中位数。
- 统计分析:在统计学中,快速计算一组数据的中位数。
5. K 个最小(或最大)元素
堆可以用于快速找到数组中的前 K 个最小(或最大)元素。通过维护一个大小为 K 的最大堆(或最小堆),可以高效地实现这一目标。
应用场景:
- 搜索引擎:在搜索引擎中,快速找到最相关的 K 个结果。
- 推荐系统:在推荐系统中,快速找到用户最感兴趣的 K 个商品或内容。
6. 图算法
堆在图算法中也有广泛应用,尤其是在处理最短路径问题(如 Dijkstra 算法)和最小生成树问题(如 Prim 算法)时。通过使用优先队列(基于堆实现),可以显著提高这些算法的效率。
应用场景:
- 最短路径:在地图导航系统中,计算从起点到终点的最短路径。
- 网络设计:在通信网络或电力网络中,设计最小生成树以最小化成本。
7. 资源管理
堆可以用于管理有限的资源,根据资源的优先级进行分配和回收。
应用场景:
- 内存管理:在操作系统中,根据内存块的大小和优先级分配内存。
- 设备调度:在多用户系统中,根据用户的优先级分配设备资源。
8. 游戏开发
在游戏开发中,堆可以用于管理游戏对象的优先级,例如:
- 事件处理:根据事件的优先级处理游戏中的事件。
- AI决策:根据决策的优先级选择最优的行动方案。
9. 分布式系统
在分布式系统中,堆可以用于管理任务队列,根据任务的优先级分配任务。
应用场景:
- 任务调度:在分布式计算中,根据任务的优先级分配计算资源。
- 负载均衡:根据服务器的负载情况,动态分配请求。
总结
堆是一种非常强大的数据结构,其高效的操作(如插入、删除和获取最值)使其在许多领域都有广泛的应用。无论是优先队列、排序算法,还是数据压缩、图算法,堆都能提供高效的解决方案。
相关文章:

青少年编程与数学 02-018 C++数据结构与算法 07课题、堆
青少年编程与数学 02-018 C数据结构与算法 07课题、堆 一、堆1. 定义2. 堆的存储方式3. 堆的常见操作4. 堆的应用 二、最大堆的实现1. 堆的存储2. 基本操作3. C代码实现4. 代码说明5. 示例输出 三、最小堆的实现四、建堆操作1. 建堆操作的原理2. 为什么从最后一个非叶子节点开始…...

机器学习特征工程中的数值分箱技术:原理、方法与实例解析
标题:机器学习特征工程中的数值分箱技术:原理、方法与实例解析 摘要: 分箱技术作为机器学习特征工程中的关键环节,通过将数值数据划分为离散区间,能够有效提升模型对非线性关系的捕捉能力,同时增强模型对异…...

安装Github软件详细流程,win10系统从配置git到安装软件详解,以及github软件整合包制作方法(
win10系统部署安装开源ai必备 一、安装git应用程序(用来下来github软件) 官网下载git的exe可执行文件,Git - Downloads 或者这里下夸克网盘分享 运行git应用程序,一路’Next’到底即可。 配置安装路径 此时如果直接运行git命…...

专业热度低,25西电光电工程学院(考研录取情况)
1、光电工程学院各个方向 2、光电工程学院近三年复试分数线对比 学长、学姐分析 由表可看出: 1、光学工程25年相较于24年下降20分, 2、光电信息与工程(专硕)25年相较于24年上升15分 3、25vs24推免/统招人数对比 学长、学姐分析…...

java—11 Redis
目录 一、Redis概述 二、Redis类型及编码 三、Redis对象的编码 1. 类型&编码的对应关系 2. string类型常用命令 (1)string类型内部实现——int编码 (2)string类型内部实现——embstr编码 编辑 (3&#x…...

C语言编程--14.电话号码的字母组合
题目: 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 示例 1: 输入:digits “23” …...

热门算法面试题第19天|Leetcode39. 组合总和40.组合总和II131.分割回文串
39. 组合总和 力扣题目链接(opens new window) 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。 说明: 所有数字(包括 ta…...
——物体跟踪)
OpenCv高阶(十一)——物体跟踪
文章目录 前言一、OpenCV 中的物体跟踪算法1、均值漂移(Mean Shift):2、CamShift:3、KCF(Kernelized Correlation Filters):4、MIL(Multiple Instance Learning)…...
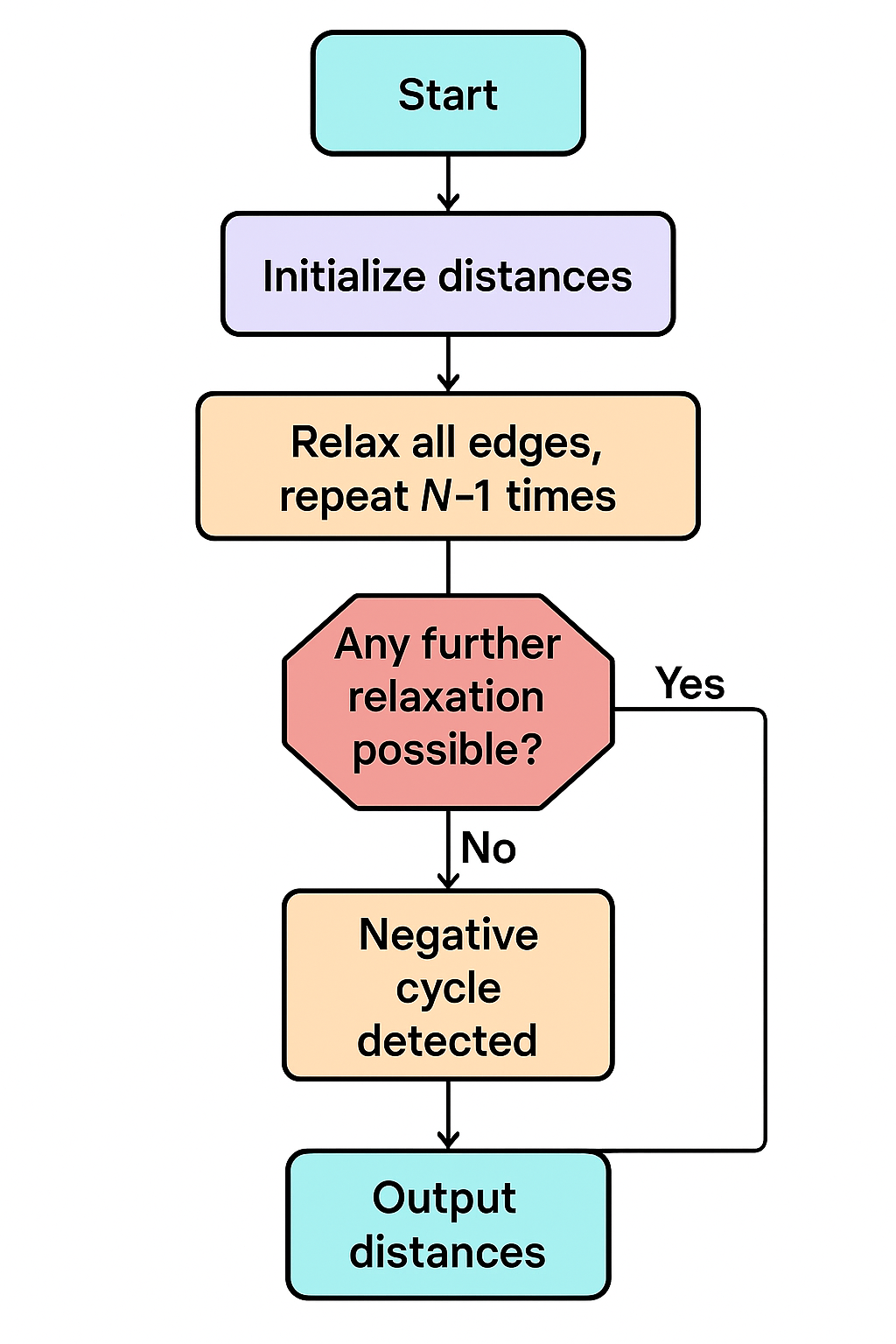
2194出差-节点开销Bellman-ford/图论
题目网址: 蓝桥账户中心 我先用Floyd跑了一遍,不出所料TLE了 n,mmap(int,input().split())clist(map(int,input().split()))INFfloat(inf) ma[[INF]*n for i in range(n)]for i in range(m):u,v,wmap(int,input().split())ma[u-1][v-1]wma[v-1][u-1]w#“…...

Docker安装beef-xss
新版的kali系统中安装了beef-xss会因为环境问题而无法启动,可以使用Docker来安装beef-xss,节省很多时间。 安装步骤 1.启动kali虚拟机,打开终端,切换到root用户,然后执行下面的命令下载beef的docker镜像 wget https:…...

产品经理学习过程
一:扫盲篇(初始产品经理) 阶段1:了解产品经理 了解产品经理是做什么的、产品经理的分类、产品经理在实际工作中都会接触什么样的岗位、以及产品经理在实际工作中具体要做什么事情。 二:准备篇 阶段2:工…...

时间序列-数据窗口进行多步预测
在时间序列预测领域,多步预测旨在基于历史数据预测未来多个时间点的值,而创建数据窗口是实现这一目标的常用且高效的技术手段。数据窗口技术的核心是通过滑动窗口机制构建训练数据集,其核心逻辑可概括为:利用历史时间步的序列模式…...

【系统架构设计师】嵌入式微处理器
目录 1. 说明2. 微处理器(MPU)3. 微控制器(MCU)4. 信号处理器(DSP)5. 图形处理器(GPU)6. 片上系统(SoC)7. 例题7.1 例题1 1. 说明 1.嵌入式微处理器主要用于处理相关任务。2.由于嵌入式系统通常都在室外使用,可能处于不同环境,因此,选择处理…...

Oracle创建触发器实例
一 创建DML 触发器 DML触发器基本要点: 触发时机:指定触发器的触发时间。如果指定为BEFORE,则表示在执行DML操作之前触发,以便防止某些错误操作发生或实现某些业务规则;如果指定为AFTER,则表示在执行DML操作…...

(三)mac中Grafana监控Linux上的Redis(Redis_exporter安装使用)
框架:GrafanaPrometheusRedis_exporter Grafana安装-CSDN博客 普罗米修斯Prometheus监控安装(mac)-CSDN博客 1.Redis_exporter安装 直接下载 wget https://github.com/oliver006/redis_exporter/releases/download/v1.0.3/redis_expor…...

Linux Sed 深度解析:从日志清洗到 K8s 等12个高频场景
看图猜诗,你有任何想法都可以在评论区留言哦~ 摘要:Sed(Stream Editor)作为 Linux 三剑客之一,凭借其流式处理与正则表达式能力,成为运维场景中文本批处理的核心工具。本文聚焦生产环境高频需求ÿ…...

基于java的网络编程入门
1. 什么是IP地址 由此可见,32位最大为255.255.255.255 打开cmd查询自己电脑的ip地址:ipconfig 测试网络是否通畅:ping 目标ip地址 2. IP地址的组成 注意:127.0.0.1是回送地址,指本地机,一般用来测试使用 …...

CV和NLP领域常见模型列表
图像分类(Image Classification) 模型名特点备注ConvNeXt V2卷积改进,媲美 Transformer强于 ResNet、EfficientNetVision Transformer (ViT)全 Transformer 架构开创图像 transformer 浪潮Swin Transformer V2局部注意力 金字塔结构更强的多…...
Git简介与入门
Git的发明 Git由著名的Linux创始人linus于2005年发明(所以git的界面、使用方式与Linux挺像的,即命令行方式) 经过发展,现在广泛应用于代码管理与团队协作。 Git特性 Git是分布式版本控制系统 分布式 每个开发者拥有完整仓库&…...

Linux 网络基础三 (数据链路层协议:以太网协议、ARP 协议)
一、以太网 两个不同局域网的主机传递数据并不是直接传递的,而是通过路由器 “一跳一跳” 的传递过去。 跨网络传输的本质:由无数个局域网(子网)转发的结果。 所以,要理解数据跨网络转发原理就要先理解一个局域网中数…...

16.QT-Qt窗口-菜单栏|创建菜单栏|添加菜单|创建菜单项|添加分割线|添加快捷键|子菜单|图标|内存泄漏(C++)
Qt窗⼝是通过QMainWindow类来实现的。 QMainWindow是⼀个为⽤⼾提供主窗⼝程序的类,继承⾃QWidget类,并且提供了⼀个预定义的布局。QMainWindow包含⼀个菜单栏(menu bar)、多个⼯具栏(tool bars)、多个浮动窗⼝(铆接部…...
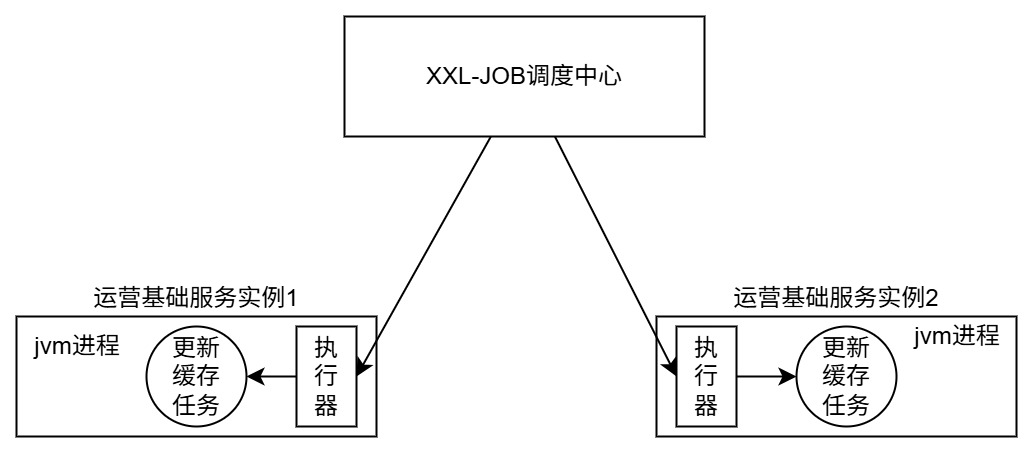
[特殊字符] 分布式定时任务调度实战:XXL-JOB工作原理与路由策略详解
在微服务架构中,定时任务往往面临多实例重复执行、任务冲突等挑战。为了解决这一问题,企业级调度框架 XXL-JOB 提供了强大的任务统一调度与执行机制,特别适合在分布式系统中使用。 本文将从 XXL-JOB 的核心架构入手,详细讲解其调…...

java面试题及答案2020,java最新面试题(四十四)
java面试题及答案2020 二面-2020/3/18 1、自我介绍项目比赛 2、java集合框架全部介绍。。从list set queue到map 3、hashmap底层扩容线程安全问题 4、如果-一个对象要作为hashmap的key需要做什么 5、Threadlocal类以及 内存泄漏 6、线程同步方式,具体每一个怎么做的 7、jvm类加…...

Spring Boot 中处理 JSON 数值溢出问题:从报错到优雅解决
一、问题背景:为什么我的接口突然报错了? 假设你正在开发一个 Spring Boot 接口,接收类似这样的 JSON 请求: {"size": 111111111111111111111 }然后突然收到用户的反馈:请求报错啦! 查看日志&a…...

oracle 锁的添加方式和死锁的解决
DML锁添加方式 DML 锁可由一个用户进程以显式的方式加锁,也可通过某些 SQL 语句隐含方式实现。 DML 锁有三种加锁方式:共享锁方式、独占锁方式、共享更新。 共享锁,独占锁用于 TM 锁,共享锁用于 TX 锁。 1)共享方式的表级锁 共享方…...

基于Hadoop的音乐推荐系统(源码+lw+部署文档+讲解),源码可白嫖!
摘要 本毕业生数据分析与可视化系统采用B/S架构,数据库是MySQL,网站的搭建与开发采用了先进的Java语言、爬虫技术进行编写,使用了Spring Boot框架。该系统从两个对象:由管理员和用户来对系统进行设计构建。主要功能包括ÿ…...

Java查询数据库表信息导出Word
参考: POI生成Word多级标题格式_poi设置word标题-CSDN博客 1.概述 使用jdbc查询数据库把表信息导出为word文档, 导出为word时需要下载word模板文件。 已实现数据库: KingbaseES, 实现代码: 点击跳转 2.效果图 2.1.生成word内容 所有数据库合并 数据库不合并 2.2.生成文件…...

DAY9:Oracle数据库安全管理深度解析
引言 在当今数据泄露事件频发的时代,数据库安全管理已成为DBA和开发者的必修课。本文将深入探讨Oracle数据库安全管理的四大核心领域:用户权限管理、数据库审计、透明数据加密(TDE)和虚拟私有数据库(VPD)&…...

RK3588平台用v4l工具调试USB摄像头实践(亮度,饱和度,对比度,色相等)
目录 前言:v4l-utils简介 一:查找当前的摄像头设备 二:查看当前摄像头支持的v4l2-ctl调试参数 三根据提示设置对应参数,在提示范围内设置 四:常用调试命令 五:应用内执行命令方法 前言:v4l-utils简介 v4l-utils工具是由Linu…...

Dart Flutter数据类型详解 int double String bool list Map
目录 字符串的几种方式 bool值的判断 List的定义方式 Map的定义方式 Dart判断数据类型 (is 关键词来判断类型) Dart的数据类型详解 int double String bool list Map 常用数据类型: Numbers(数值): int double Strings(字符串) String Booleans(布尔…...
