二项分布详解:从基础到应用
二项分布详解:从基础到应用
目录
- 引言
- 二项分布的定义
- 概率质量函数及其证明
- 期望与方差推导
- 二项分布的重要性质
- 常见应用场景
- 与其他分布的关系
- 知识梳理
- 练习与思考
引言
概率论中,二项分布是最基础也是最常用的离散概率分布之一。它描述了在固定次数的独立重复试验中,成功次数的概率分布。从抛硬币到质量控制,从生物实验到网络安全,二项分布的应用无处不在。
二项分布的定义
伯努利试验
在介绍二项分布前,我们需要先明确伯努利试验(Bernoulli trial)的概念:
- 每次试验只有两种可能结果:成功或失败
- 每次试验成功的概率为p,保持不变
- 各次试验之间相互独立
二项分布定义
当我们进行n次独立同分布的伯努利试验,并记录成功的次数X,则随机变量X服从二项分布,记为:
X ∼ B ( n , p ) X \sim B(n,p) X∼B(n,p)
其中:
- n表示试验次数(正整数)
- p表示单次试验成功概率(0≤p≤1)
- X表示n次试验中成功的次数
概率质量函数及其证明
PMF公式
若随机变量X服从参数为(n,p)的二项分布,则其概率质量函数为:
P ( X = k ) = ( n k ) p k ( 1 − p ) n − k , k = 0 , 1 , 2 , . . . , n P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k=0,1,2,...,n P(X=k)=(kn)pk(1−p)n−k,k=0,1,2,...,n
其中 ( n k ) = n ! k ! ( n − k ) ! \binom{n}{k} = \frac{n!}{k!(n-k)!} (kn)=k!(n−k)!n!是组合数,表示从n个位置中选择k个位置的方法数。
证明过程
我们可以从以下角度进行证明:
-
问题模型化:在n次伯努利试验中,我们关心恰好获得k次成功的概率。
-
单一序列概率:考虑一个特定序列,比如"成功,失败,成功,…,失败",其中恰好有k次成功和(n-k)次失败。该特定序列出现的概率是:
p k ⋅ ( 1 − p ) n − k p^k \cdot (1-p)^{n-k} pk⋅(1−p)n−k -
序列计数:对于n次试验,有多少种不同的序列恰好包含k次成功?
- 这等价于从n个位置中选择k个位置放置"成功"的结果
- 方法数为组合数 ( n k ) \binom{n}{k} (kn)
-
总概率计算:根据乘法原理,恰好有k次成功的概率等于:
P ( X = k ) = ( n k ) p k ( 1 − p ) n − k P(X=k) = \binom{n}{k} p^k (1-p)^{n-k} P(X=k)=(kn)pk(1−p)n−k
这就是二项分布的概率质量函数。
期望与方差推导
期望
二项分布 B ( n , p ) B(n,p) B(n,p)的期望为:
E ( X ) = n p E(X) = np E(X)=np
证明:
我们可以将X表示为n个伯努利随机变量的和:
X = X 1 + X 2 + . . . + X n X = X_1 + X_2 + ... + X_n X=X1+X2+...+Xn
其中 X i X_i Xi表示第i次试验的结果(成功为1,失败为0)。
由于 E ( X i ) = p E(X_i) = p E(Xi)=p且期望具有线性性质,所以:
E ( X ) = E ( X 1 + X 2 + . . . + X n ) = E ( X 1 ) + E ( X 2 ) + . . . + E ( X n ) = n p E(X) = E(X_1 + X_2 + ... + X_n) = E(X_1) + E(X_2) + ... + E(X_n) = np E(X)=E(X1+X2+...+Xn)=E(X1)+E(X2)+...+E(Xn)=np
方差
二项分布 B ( n , p ) B(n,p) B(n,p)的方差为:
V a r ( X ) = n p ( 1 − p ) Var(X) = np(1-p) Var(X)=np(1−p)
证明:
同样,将X表示为n个伯努利随机变量的和:
X = X 1 + X 2 + . . . + X n X = X_1 + X_2 + ... + X_n X=X1+X2+...+Xn
由于各 X i X_i Xi相互独立,且 V a r ( X i ) = p ( 1 − p ) Var(X_i) = p(1-p) Var(Xi)=p(1−p),我们有:
V a r ( X ) = V a r ( X 1 + X 2 + . . . + X n ) = V a r ( X 1 ) + V a r ( X 2 ) + . . . + V a r ( X n ) = n p ( 1 − p ) Var(X) = Var(X_1 + X_2 + ... + X_n) = Var(X_1) + Var(X_2) + ... + Var(X_n) = np(1-p) Var(X)=Var(X1+X2+...+Xn)=Var(X1)+Var(X2)+...+Var(Xn)=np(1−p)
二项分布的重要性质
1. 可加性
如果 X ∼ B ( n , p ) X \sim B(n,p) X∼B(n,p)且 Y ∼ B ( m , p ) Y \sim B(m,p) Y∼B(m,p),并且X与Y独立,则 X + Y ∼ B ( n + m , p ) X+Y \sim B(n+m,p) X+Y∼B(n+m,p)。
2. 对称性
当 p = 0.5 p = 0.5 p=0.5时,二项分布关于 n 2 \frac{n}{2} 2n对称,即 P ( X = k ) = P ( X = n − k ) P(X=k) = P(X=n-k) P(X=k)=P(X=n−k)。
3. 递推公式
对于概率质量函数,存在以下递推关系:
P ( X = k + 1 ) = P ( X = k ) ⋅ p 1 − p ⋅ n − k k + 1 P(X=k+1) = P(X=k) \cdot \frac{p}{1-p} \cdot \frac{n-k}{k+1} P(X=k+1)=P(X=k)⋅1−pp⋅k+1n−k
4. 最可能值(众数)
二项分布 B ( n , p ) B(n,p) B(n,p)的众数为:
- 当 ( n + 1 ) p (n+1)p (n+1)p不是整数时,众数为 ⌊ ( n + 1 ) p ⌋ \lfloor (n+1)p \rfloor ⌊(n+1)p⌋
- 当 ( n + 1 ) p (n+1)p (n+1)p是整数时,众数有两个: ( n + 1 ) p − 1 (n+1)p-1 (n+1)p−1和 ( n + 1 ) p (n+1)p (n+1)p
5. 分布函数
二项分布的累积分布函数为:
F ( k ) = P ( X ≤ k ) = ∑ i = 0 ⌊ k ⌋ ( n i ) p i ( 1 − p ) n − i F(k) = P(X \leq k) = \sum_{i=0}^{\lfloor k \rfloor} \binom{n}{i} p^i (1-p)^{n-i} F(k)=P(X≤k)=i=0∑⌊k⌋(in)pi(1−p)n−i
常见应用场景
-
质量控制:在抽样检验中,检测n个产品中不合格品的数量。
-
医学试验:在n个患者中,有多少人对某种治疗方法有反应。
-
市场调查:在n个受访者中,有多少人愿意购买新产品。
-
网络安全:n次入侵尝试中,成功突破防御的次数。
-
金融风险:n个投资项目中,盈利项目的数量。
实例分析
例1:硬币投掷
投掷10次公平硬币,恰好出现6次正面的概率为:
P ( X = 6 ) = ( 10 6 ) ( 0.5 ) 6 ( 0.5 ) 4 = 210 ⋅ ( 0.5 ) 10 = 210 ⋅ 1 1024 ≈ 0.205 P(X=6) = \binom{10}{6} (0.5)^6 (0.5)^4 = 210 \cdot (0.5)^{10} = 210 \cdot \frac{1}{1024} \approx 0.205 P(X=6)=(610)(0.5)6(0.5)4=210⋅(0.5)10=210⋅10241≈0.205
例2:生产质量
某产品的不良率为3%,随机抽查50件产品,恰好发现2件不良品的概率为:
P ( X = 2 ) = ( 50 2 ) ( 0.03 ) 2 ( 0.97 ) 48 ≈ 0.228 P(X=2) = \binom{50}{2} (0.03)^2 (0.97)^{48} \approx 0.228 P(X=2)=(250)(0.03)2(0.97)48≈0.228
与其他分布的关系
泊松近似
当n很大且p很小,使得np保持适中时,二项分布可以用参数λ=np的泊松分布近似:
P ( X = k ) ≈ e − λ λ k k ! P(X=k) \approx \frac{e^{-\lambda}\lambda^k}{k!} P(X=k)≈k!e−λλk
正态近似
根据中心极限定理,当n足够大时,二项分布可以用正态分布近似:
X ≈ N ( n p , n p ( 1 − p ) ) X \approx N(np, np(1-p)) X≈N(np,np(1−p))
通常当 n p > 5 np>5 np>5且 n ( 1 − p ) > 5 n(1-p)>5 n(1−p)>5时,这种近似效果较好。
知识梳理
下面通过思维导图来梳理二项分布的核心知识点:
flowchart TDA[二项分布 B(n,p)]A --> B[定义与参数]B --> B1[n: 试验次数]B --> B2[p: 成功概率]B --> B3[X: 成功次数]A --> C[概率质量函数]C --> C1["P(X=k) = C(n,k) * p^k * (1-p)^(n-k)"]A --> D[数字特征]D --> D1[期望: E(X) = np]D --> D2[方差: Var(X) = np(1-p)]D --> D3[标准差: σ = √(np(1-p))]A --> E[重要性质]E --> E1[可加性]E --> E2[对称性]E --> E3[递推公式]E --> E4[众数]A --> F[应用场景]F --> F1[质量控制]F --> F2[医学试验]F --> F3[金融风险]F --> F4[市场调查]A --> G[近似]G --> G1[泊松近似]G --> G2[正态近似]A --> H[特殊情况]H --> H1[p=0时退化为常数0]H --> H2[p=1时退化为常数n]H --> H3[n=1时退化为伯努利分布]
练习与思考
-
基础计算:投掷一枚偏心硬币5次,每次正面概率为0.6,求恰好出现3次正面的概率。
-
实际应用:某疫苗的有效率为95%,对100人接种后,求至少有90人产生免疫力的概率。
-
思考题:如何用二项分布解释"回归均值"现象?
-
推广问题:如果成功概率p在每次试验中可能不同,我们应该如何修改模型?
通过本文的学习,相信大家已经对二项分布有了全面的理解。二项分布作为概率论的基础知识,不仅在理论上有着优雅的数学性质,更在实践中有着广泛的应用。掌握它将为学习更高级的概率模型打下坚实基础。
欢迎在评论区分享你的想法和问题!
相关文章:

二项分布详解:从基础到应用
二项分布详解:从基础到应用 目录 引言二项分布的定义概率质量函数及其证明期望与方差推导二项分布的重要性质常见应用场景与其他分布的关系知识梳理练习与思考 引言 概率论中,二项分布是最基础也是最常用的离散概率分布之一。它描述了在固定次数的独…...

CentOS 7上Memcached的安装、配置及高可用架构搭建
Memcached是一款高性能的分布式内存缓存系统,常用于加速动态Web应用的响应。本文将在CentOS 7上详细介绍Memcached的安装、配置,以及如何实现Memcached的高可用架构。 (1)、搭建memcached 主主复制架构 Memcached 的复制功能支持…...

如何让 HTML 文件嵌入另一个 HTML 文件:详解与实践
目录 一、为什么需要在HTML中嵌入其他HTML文件? 二、常用的方法概览 三、利用 1. 基本原理 2. 使用场景 3. 优缺点 4. 实践示例 5. 适用建议 四、利用JavaScript动态加载内容 1. 原理简介 2. 实现步骤 示例代码 3. 优缺点分析 4. 应用场景 5. 实践建…...

mac brew 无法找到php7.2 如何安装php7.2
mac brew 无法找到php7.2 如何安装php7.2 原因是升级过高版本的brew后已经不支持7.2了,但可以通过第三方工具来安装 brew tap shivammathur/php brew install shivammathur/php/php7.2标题安装完成后会提示以下信息: The php.ini and php-fpm.ini fil…...

人工智能与机器学习:Python从零实现逻辑回归模型
🧠 向所有学习者致敬! “学习不是装满一桶水,而是点燃一把火。” —— 叶芝 我的博客主页: https://lizheng.blog.csdn.net 🌐 欢迎点击加入AI人工智能社区! 🚀 让我们一起努力,共创…...

windows服务器及网络:搭建FTP服务器
前言:(各位大佬们,昨天太忙了,整得没有发布昨天那该写的那一篇,属实有点可惜的说QAQ,不过问题已经解决,我又回来啦) 今天我要介绍的是在Windows中关于搭建FTP服务器的流程与方法 注…...
-接口API)
Python学习之路(五)-接口API
在 Python 中结合数据库开发接口 API 通常使用 Web 框架(如 Flask 或 Django)和 ORM(对象关系映射)工具(如 SQLAlchemy 或 Django ORM)。以下是使用 Flask 和 SQLAlchemy 的详细步骤,展示如何结合数据库开发一个简单的 API。 使用 Flask 和 SQLAlchemy 开发 API 1. 安…...

欧拉计划 Project Euler56(幂的数字和)题解
欧拉计划 Project Euler 56 题解 题干思路code 题干 思路 直接暴力枚举即可,用c要模拟大数的乘法,否则会溢出 code // 972 #include <bits/stdc.h>using namespace std;using ll long long;string mul(const string &num1, int num2) {int…...

C++初窥门径
const关键字 一、const关键字 修饰成员变量 常成员变量:必须通过构造函数的初始化列表进行初始化,且初始化后不可修改。 示例: class Student { private: const int age; // 常成员变量 public: Student(string name, int age) : age(ag…...

AlarmClock4.8.4(官方版)桌面时钟工具软件下载安装教程
1.软件名称:AlarmClock 2.软件版本:4.8.4 3.软件大小:187 MB 4.安装环境:win7/win10/win11(64位) 5.下载地址: https://www.kdocs.cn/l/cdZMwizD2ZL1?RL1MvMTM%3D 提示:先转存后下载,防止资…...

白鲸开源WhaleStudio与崖山数据库管理系统YashanDB完成产品兼容互认证
近日,北京白鲸开源科技有限公司与深圳计算科学研究院联合宣布,双方已完成产品兼容互认证。此次认证涉及深圳计算科学研究院自主研发的崖山数据库管理系统YashanDB V23和北京白鲸开源科技有限公司的核心产品WhaleStudio V2.6。经过严格的测试与验证&#…...

【金仓数据库征文】- 金融HTAP实战:KingbaseES实时风控与毫秒级分析一体化架构
文章目录 引言:金融数字化转型的HTAP引擎革命一、HTAP架构设计与资源隔离策略1.1 混合负载物理隔离架构1.1.1 行列存储分区策略1.1.2 四级资源隔离机制 二、实时流处理与增量同步优化2.1 分钟级新鲜度保障2.1.1 WAL日志增量同步2.1.2 流计算优化 2.2 物化视图实时刷…...

云服务器centos 安装hadoop集群
百度 搜索 云服务器centos 安装hadoop 创建Hadoop用户 sudo useradd hadoop -m -s /bin/bash sudo passwd hadoop 123456 下载Hadoop wget https://mirrors.tuna.tsinghua.edu.cn/apache/hadoop/common/hadoop-3.2.4/hadoop-3.2.4.tar.gz 解压并移动Hadoop到指定目录 tar …...
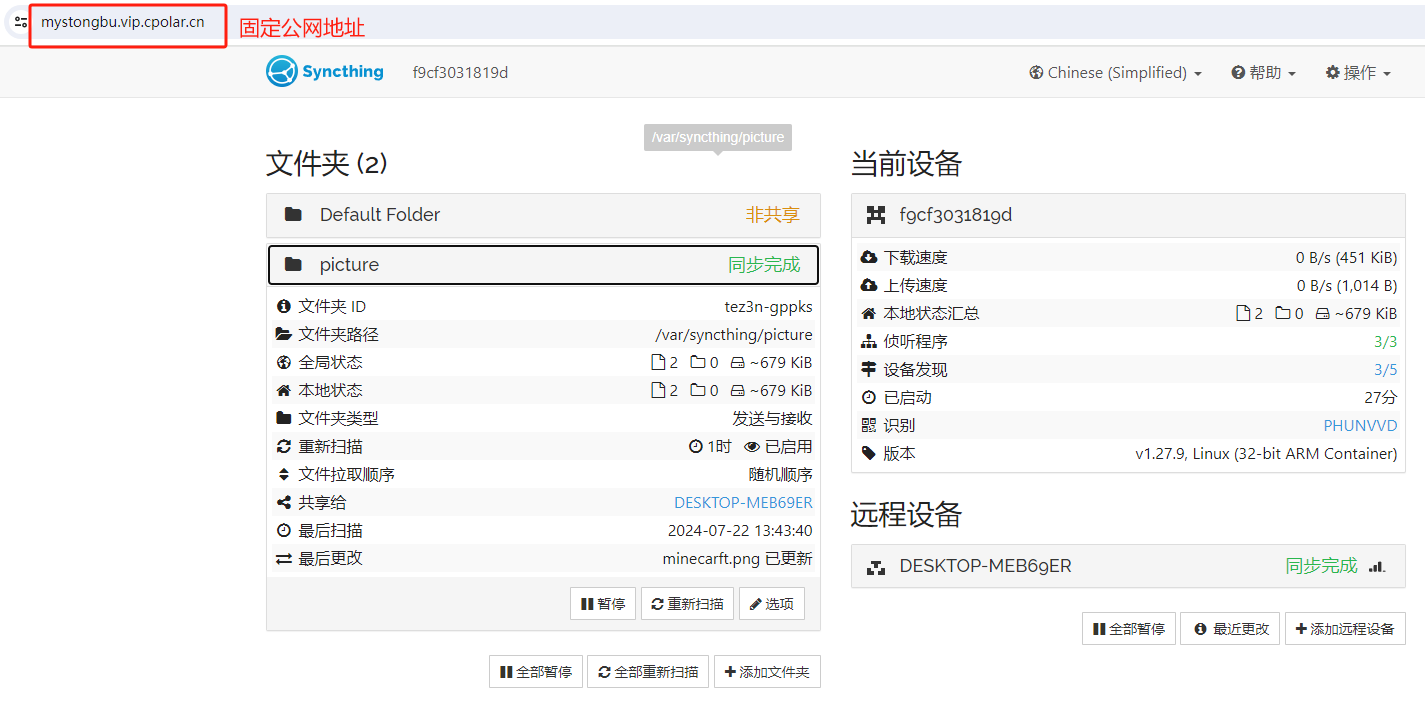
Windows与CasaOS跨平台文件同步:SyncThing本地部署与同步配置流程
文章目录 前言1. 添加镜像源2. 应用安装测试3. 安装syncthing3.1 更新应用中心3.2 SyncThing安装与配置3.3 Syncthing使用演示 4. 安装内网穿透工具5. 配置公网地址6. 配置固定公网地址 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽…...

59、微服务保姆教程(二)Nacos--- 微服务 注册中心 + 配置中心
Nacos— 微服务 注册中心 + 配置中心 一.什么是Nacos? Nacos是阿里的一个开源产品,是针对微服务架构中的服务发现、配置管理、服务治理的综合型解决方案。 Nacos核心定位是“一个更易于帮助构建云原生应用的动态服务发现、配置和服务管理平台”,也就是我们的注册中心和配…...

第一部分:git基本操作
目录 1、git初识 1.1、存在的问题 1.2、版本控制器 1.3、git安装 1.3.1、CentOS平台 1.3.2、ubuntu平台 2、git基本操作 2.1、创建仓库 2.2、配置git 3、工作区、暂存区、版本库 4、基本操作 4.1、场景一 4.2、场景二 4.3、修改文件 5、版本回退 6、撤销修改 …...

《一文读懂Transformers库:开启自然语言处理新世界的大门》
《一文读懂Transformers库:开启自然语言处理新世界的大门》 GitHub - huggingface/transformers: 🤗 Transformers: State-of-the-art Machine Learning for Pytorch, TensorFlow, and JAX. HF-Mirror Hello! Transformers快速入门 pip install transformers -i https:/…...

2025年GPLT团体程序设计天梯赛L1-L2
目录 1.珍惜生命 2.偷感好重 3.高温补贴 4.零头就抹了吧 5.这是字符串题 6.这不是字符串题 7.大幂数编辑 8.现代战争编辑 9.算式拆解 10.三点共线 11.胖达的山头 12.被n整除的n位数 1.珍惜生命 【解析】直接输出即可 #include<bits/stdc.h> using namespace…...

【每天一个知识点】IPv4(互联网协议版本4)和IPv6(互联网协议版本6)
IPv4(互联网协议版本4)和IPv6(互联网协议版本6)是用于在互联网上标识和定位设备的两种主要协议。它们的主要区别在于地址空间、结构、以及一些附加功能。以下是两者的对比: 1. 地址长度 IPv4: 地址长度为32位…...

金仓数据库征文-政务领域国产化数据库更替:金仓 KingbaseES 应用实践
目录 一.金仓数据库介绍 二.政务领域数据库替换的时代需求 三.金仓数据库 KingbaseES 在政务领域的替换优势 1.强大的兼容性与迁移能力 2.高安全性与稳定性保障 3.良好的国产化适配性 四.金仓数据库 KingbaseES 在政务领域的典型应用实践 1.电子政务办公系…...

Mac 「brew」快速安装MySQL
安装MySQL 在 macOS 上安装 MySQL 环境可以通过Homebrew快速实现,以下是步骤指南: 方法 1:使用 Homebrew 安装 MySQL 1. 安装 Homebrew 如果尚未安装 Homebrew,可以通过以下命令安装: /bin/bash -c "$(curl -…...

Android Studio开发中Application和Activity生命周期详解
文章目录 Application生命周期Application生命周期概述Application关键回调方法onCreate()onConfigurationChanged()onLowMemory()onTrimMemory()onTerminate() Application生命周期管理最佳实践 Activity生命周期Activity生命周期概述Activity生命周期回调方法onCreate()onSta…...

【一次成功!】Ubuntu22.04 安装 Autoware、 cuda、 cudnn、 TensorRT
背景 新买的工控机,32GB NVIDIA GeForce RTX 4060,只装了 Ubuntu22.04、ROS2 Humble。 一.安装Autoware Source installation - Autoware Documentation 1. 基础环境 OS Ubuntu 22.04ROS ROS 2 Humble#小鱼ros一键安装 wget http://fishros.com/install -O fishros &…...

【金仓数据库征文】金仓数据库:开启未来技术脑洞,探索数据库无限可能
我的个人主页 我的专栏: 人工智能领域、java-数据结构、Javase、C语言,希望能帮助到大家!!! 点赞👍收藏❤ 目录 引言:数据库进化的下一站 —— 未来科技的无限可能金仓数据库简介:国…...

微信小程序根据图片生成背景颜色有效果图
效果图 取得是图片中间10个像素算出背景颜色 .wxml <canvas type"2d" id"imageCanvas" style"--w: {{w}}px;--h: {{h}}px;" /> <view style"background: {{backgroundColor}};"><image bind:tap"updateIndex&qu…...

Redis ⑥-string | hash | list
string类型基本介绍 Redis 中的字符串,是直接按照二进制的方式进行存储的。也就是说,在存取的过程中,是不会做任何编码转换的。存的是啥,取的时候就是啥。 Redis 的这个机制,就使得 Redis 非常适合用来存储各种各样的…...

深入理解C语言函数之模拟实现strcpy()strcat()
文章目录 前言一、strcpy的模拟实现二、strcat的模拟实现总结 前言 前面我们用三种方法模拟实现了一下strlen,所以这篇文章模拟实现以下strcpy()strcat() 一、strcpy的模拟实现 首先我们去官网找到strcpy的用法和原…...

大数据组件学习之--Kafka 安装搭建
一、前置环境 在搭建kafka之前,请确认自己的hadoop、zookeeper是否搭建完成且可正常运行 二、下载并上传安装包(链接为百度网盘) kafka安装包 tar -zxvf /opt/software/kafka_2.12-2.4.1.tgz -C /opt/module/ 进入解压后的目录更改文件名…...

BIOS主板(非UEFI)安装fedora42的方法
BIOS主板(非UEFI)安装fedora42的方法 现实困难:将Fedora-Workstation-Live-42-1.1.x86_64.iso写入U盘制作成可启动U盘启动fedora42,按照向导将fedora42安装到真机的sda7分区中得到报错如下内容: /boot/efi 必需的 /boot/efi必须位于格式化为e…...

[吾爱出品] 【键鼠自动化工具】支持识别窗口、识图、发送文本、按键组合等
键鼠自动化工具 链接:https://pan.xunlei.com/s/VOOhDZkj-E0mdDZCvo3jp6s4A1?pwdfufb# 1、增加的找图点击功能(不算增加,只能算缝补),各种的不完善,但是能运行。 2、因为受限于原程序的界面,…...
