STM32F103RC中ADC1和ADC2通道复用
以下是STM32F103RC中ADC1和ADC2通道复用的示意图及文字说明,帮助直观理解这种共享关系:
ADC1/ADC2引脚复用示意图
GPIO引脚 ADC1通道 ADC2通道
┌─────────┐ ┌─────────┐ ┌─────────┐
│ PA0 ├───┤ ADC1_IN0├─┬─┤ ADC2_IN0│
├─────────┤ ├─────────┤ │ ├─────────┤
│ PA1 ├───┤ ADC1_IN1├─┬─┤ ADC2_IN1│
├─────────┤ ├─────────┤ │ ├─────────┤
│ ... │ │ ... │ │ │ ... │
├─────────┤ ├─────────┤ │ ├─────────┤
│ PC5 ├───┤ADC1_IN15├─┬─┤ADC2_IN15│
└─────────┘ └─────────┘ │ └─────────┘│
内部信号通道 │
┌─────────────────────┐ │
│ ADC1_IN16 (温度传感器)│ │
├─────────────────────┤ │
│ ADC1_IN17 (VREFINT) │ │
└─────────────────────┘ │││
┌─────────────────────┐ │
│ ADC2_IN16 (温度传感器├───┘
├─────────────────────┤
│ ADC2_IN17 (VREFINT) │
└─────────────────────┘
以下是用简单示意图来帮助理解STM32F103RC的ADC1和ADC2外部通道与GPIO引脚关系:
整体框架图
+---------------------+| STM32F103RC芯片 |+---------------------+|| (内部连接)|+---------------------+| ADC1模块 |+---------------------+|| (复用连接)|+---------------------+| GPIO引脚组(PA0 - PC5)|+---------------------+|| (复用连接)|+---------------------+| ADC2模块 |+---------------------+
具体通道对应关系展开图
| GPIO引脚 | ADC1通道 | ADC2通道 |
|---|---|---|
| PA0 | IN0 | IN0 |
| PA1 | IN1 | IN1 |
| PA2 | IN2 | IN2 |
| PA3 | IN3 | IN3 |
| PA4 | IN4 | IN4 |
| PA5 | IN5 | IN5 |
| PA6 | IN6 | IN6 |
| PA7 | IN7 | IN7 |
| PB0 | IN8 | IN8 |
| PB1 | IN9 | IN9 |
| PC0 | IN10 | IN10 |
| PC1 | IN11 | IN11 |
| PC2 | IN12 | IN12 |
| PC3 | IN13 | IN13 |
| PC4 | IN14 | IN14 |
| PC5 | IN15 | IN15 |
这表示STM32F103RC芯片内,ADC1和ADC2的16个外部通道(IN0 - IN15 )在物理上都连接到了PA0 - PC5这些GPIO引脚上,在使用时可根据需求配置这些引脚作为ADC通道来采集模拟信号 。
关键点解析
-
外部通道共享
- 每个GPIO引脚(如PA0)同时连接到ADC1和ADC2的对应通道。
- 例如:PA0同时是
ADC1_IN0和ADC2_IN0,但同一时间只能被一个ADC模块采样。
-
内部通道独立
- 温度传感器(IN16)和内部参考电压(IN17)在ADC1和ADC2中逻辑上独立,但物理上来自同一个传感器源。
-
冲突示例
- 若同时配置
ADC1_IN0和ADC2_IN0采样PA0,会导致硬件竞争,结果不可预测。
- 若同时配置
实际电路等效模型
PA0引脚│├───[ADC1 MUX]─── ADC1_IN0│└───[ADC2 MUX]─── ADC2_IN0
- MUX(多路复用器):STM32内部通过电子开关切换ADC1或ADC2连接到引脚。
使用规则总结
-
允许的操作
- ADC1采样PA0,ADC2采样PA1(不同引脚)。
- ADC1和ADC2分时复用PA0(非同步)。
-
禁止的操作
- ADC1和ADC2同时采样PA0(硬件冲突)。
- ADC1和ADC2同时启用扫描模式并包含同一引脚。
代码示例(安全用法)
// 安全配置:ADC1用PA0,ADC2用PA1
ADC_RegularChannelConfig(ADC1, ADC_Channel_0, 1, ADC_SampleTime_55Cycles5); // PA0
ADC_RegularChannelConfig(ADC2, ADC_Channel_1, 1, ADC_SampleTime_55Cycles5); // PA1// 危险配置(冲突!)
ADC_RegularChannelConfig(ADC1, ADC_Channel_0, 1, ADC_SampleTime_55Cycles5); // PA0
ADC_RegularChannelConfig(ADC2, ADC_Channel_0, 1, ADC_SampleTime_55Cycles5); // PA0
通过这种共享设计,STM32在有限的引脚下实现了多ADC灵活性,但需开发者注意合理分配资源。
相关文章:

STM32F103RC中ADC1和ADC2通道复用
以下是STM32F103RC中ADC1和ADC2通道复用的示意图及文字说明,帮助直观理解这种共享关系: ADC1/ADC2引脚复用示意图 GPIO引脚 ADC1通道 ADC2通道 ┌─────────┐ ┌─────────┐ ┌─────────┐ │ PA0 ├─…...

Qt—鼠标移动事件的趣味小程序:会移动的按钮
1.项目目标 本次根据Qt的鼠标移动事件实现一个趣味小程序:当鼠标移动到按钮时,按钮就会随机出现在置,以至于根本点击不到按钮。 2.项目步骤 首先现在ui界面设计控件(也可以用代码的方式创建,就不多说了) 第一个按钮不需…...

鞋样设计软件
Sxy 64鞋样设计软件是一款专业级鞋类设计工具 专为鞋业设计师与制鞋企业开发 该软件提供全面的鞋样设计功能 包括二维开版 三维建模 放码排料等核心模块 支持从草图构思到成品输出的完整设计流程 内置丰富的鞋型数据库与部件库 可快速生成各种鞋款模板 软件采用智能放码技术 精…...

LeRobot 项目部署运行逻辑(六)——visualize_dataset_html.py/visualize_dataset.py
可视化脚本包括了两个方法:远程下载 huggingface 上的数据集和使用本地数据集 脚本主要使用两个: 目前来说,ACT 采集训练用的是统一时间长度的数据集,此外,这两个脚本最大的问题在于不能裁剪,这也是比较好…...

Windows Server 2025开启GPU分区(GPU-P)部署DoraCloud云桌面
本文描述在ShareStation工作站虚拟化方案的部署过程。 将服务器上部署 Windows Server、DoraCloud,并创建带有vGPU的虚拟桌面。 GPU分区技术介绍 GPU-P(GPU Partitioning) 是微软在 Windows 虚拟化平台(如 Hyper-V)中…...
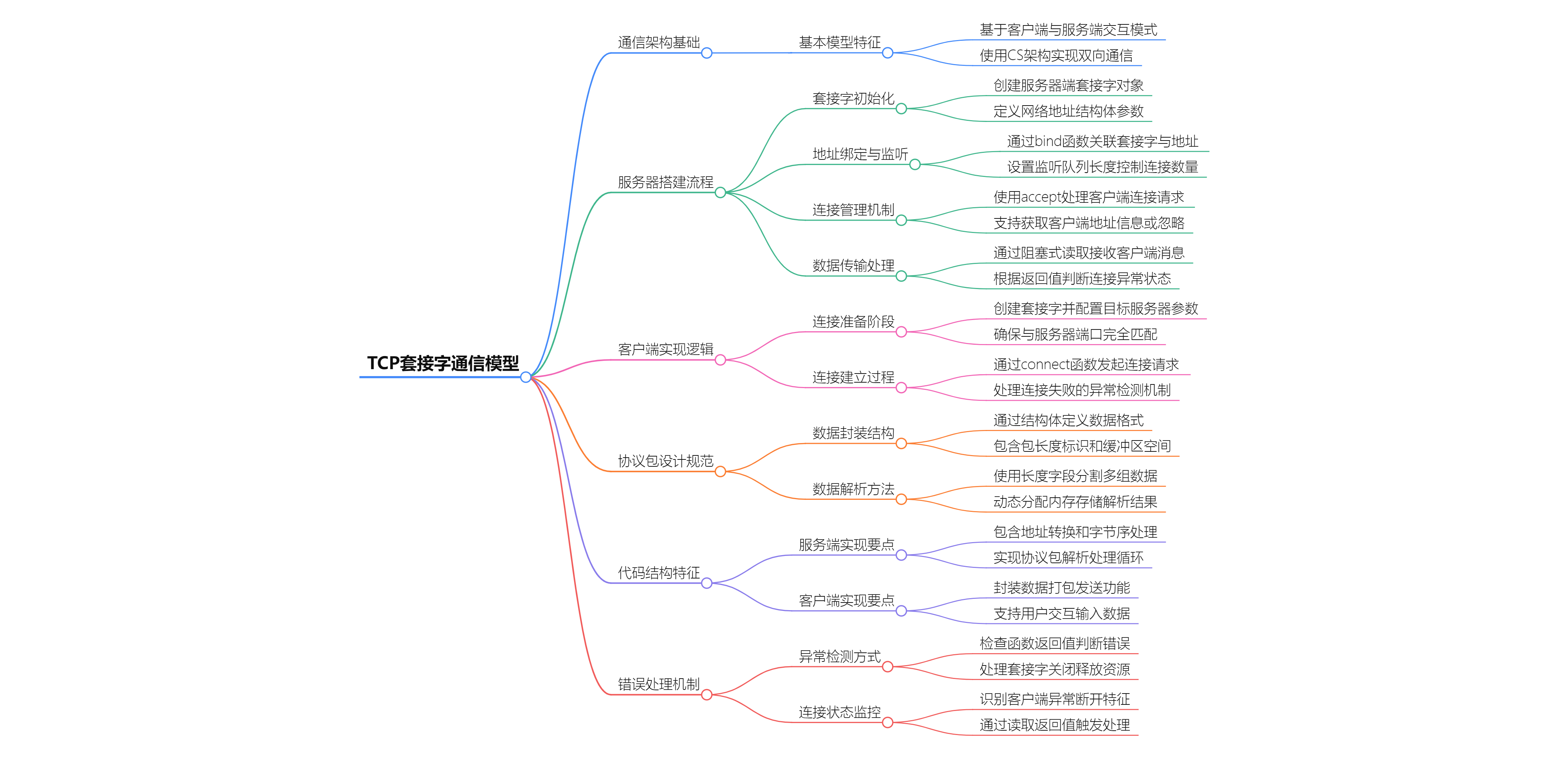
TCP套接字通信核心要点
TCP套接字通信核心要点 通信模型架构 客户端-服务端模型 CS架构:客户端发起请求,服务端响应和处理请求双向通道:建立连接后实现全双工通信 服务端搭建流程 核心步骤 创建套接字 int server socket(AF_INET, SOCK_STREAM, 0); 参数说明&am…...
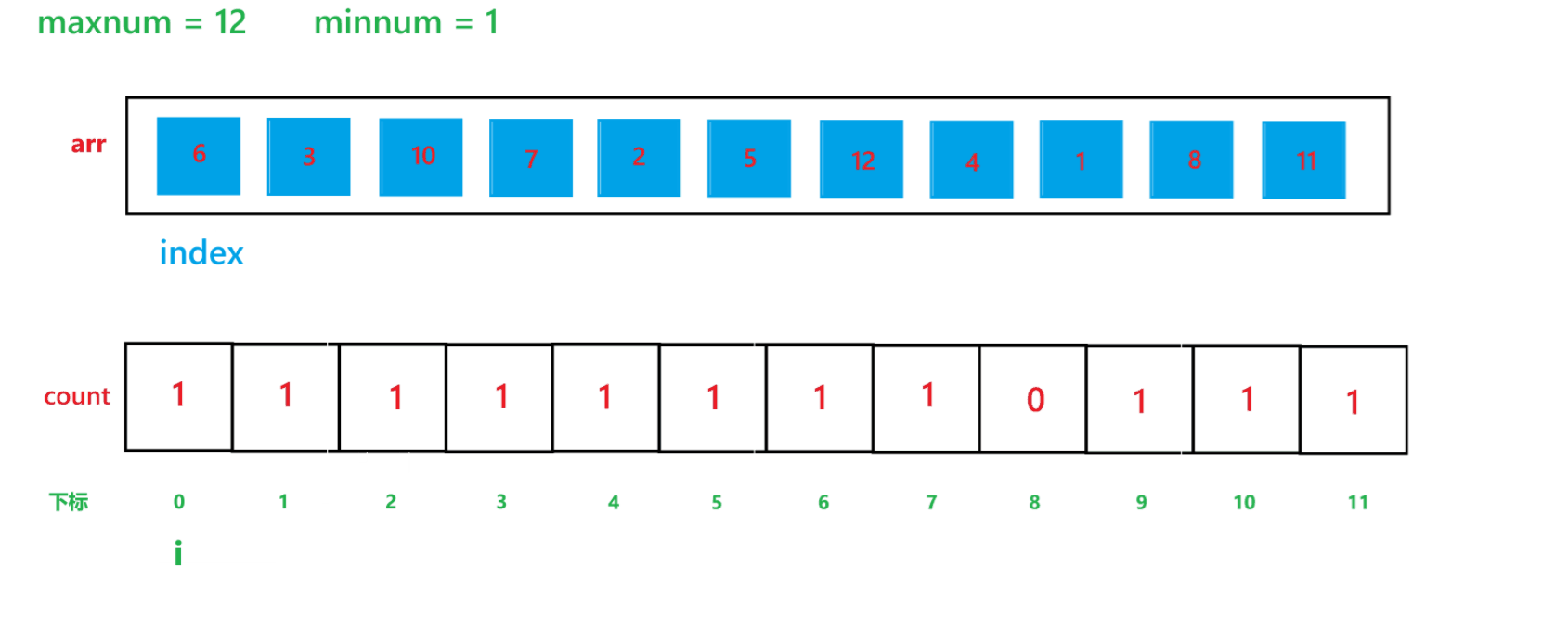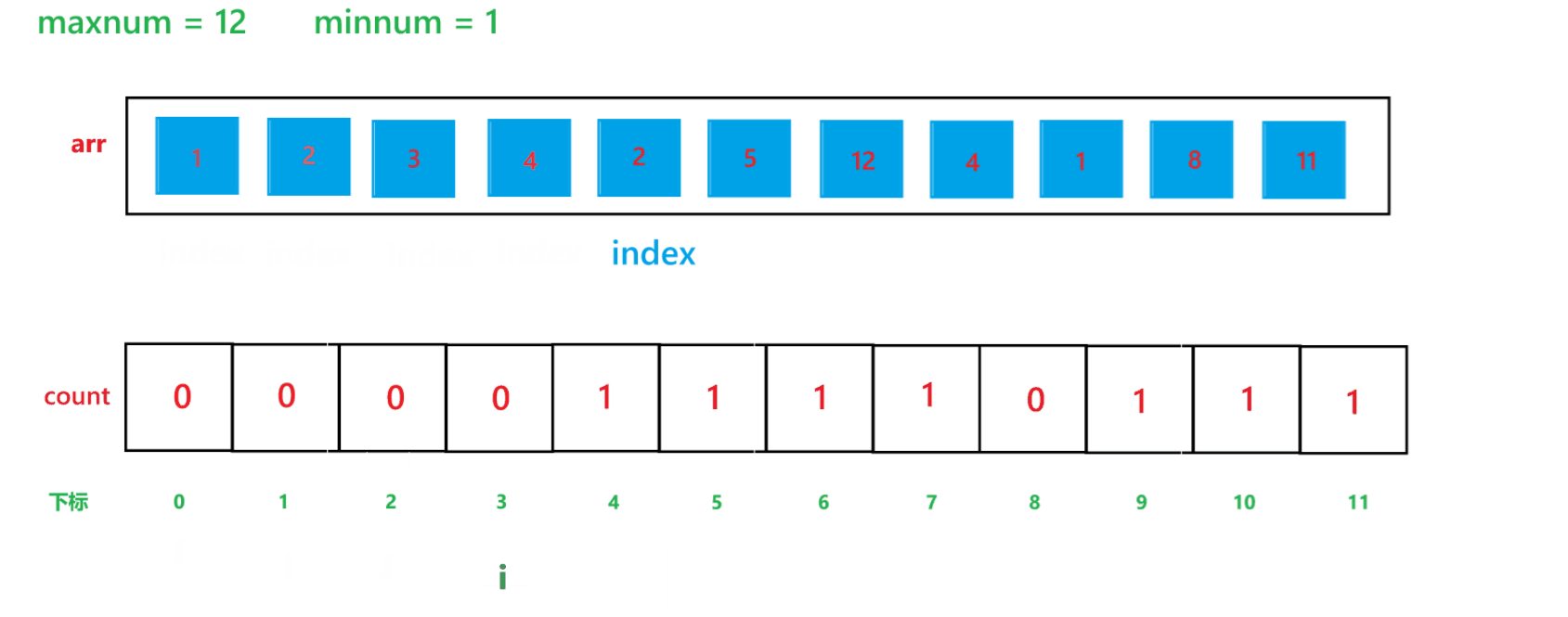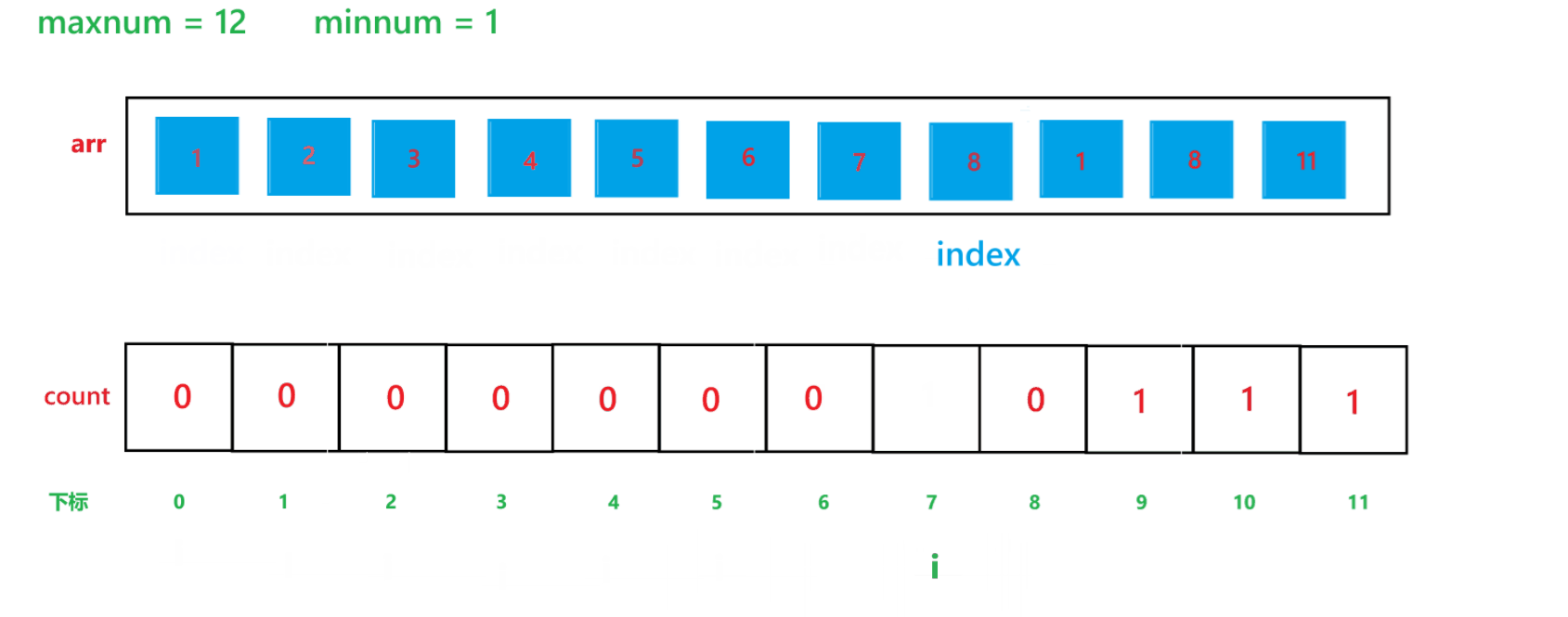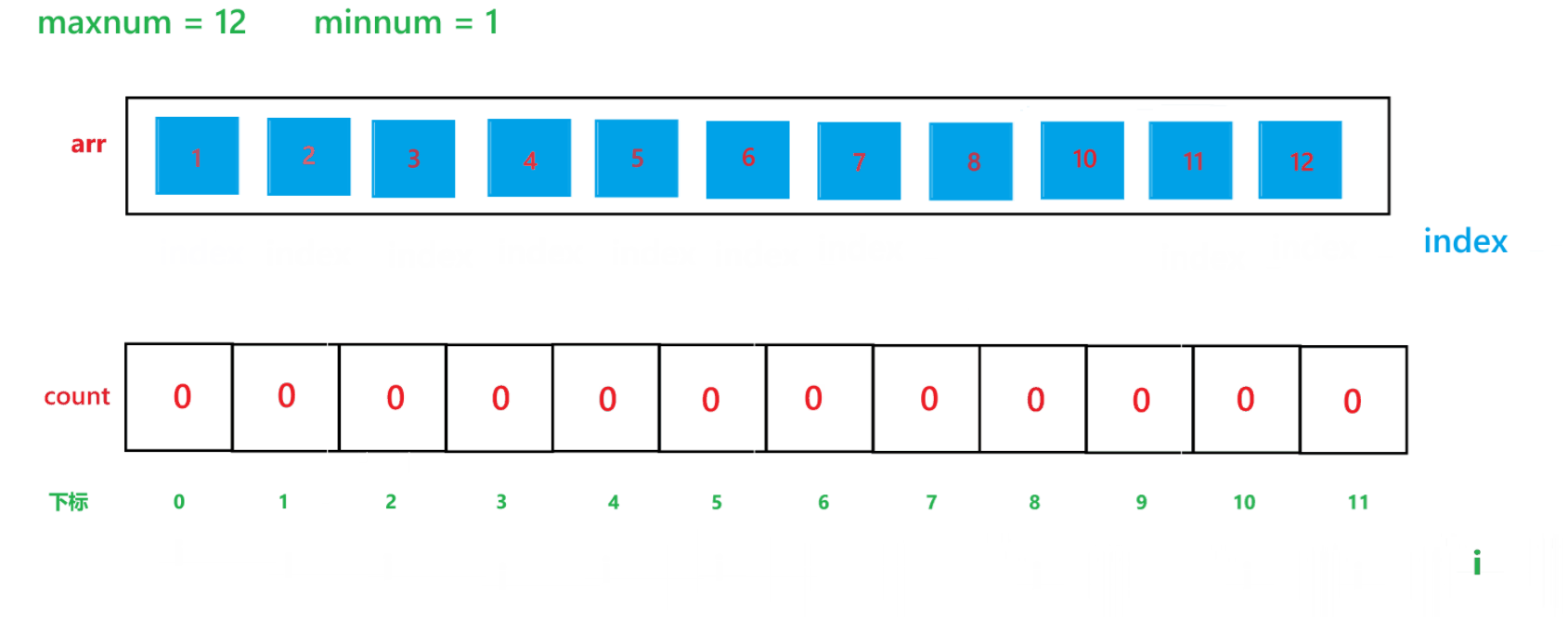
【C】初阶数据结构15 -- 计数排序与稳定性分析
本文主要讲解七大排序算法之外的另一种排序算法 -- 计数排序 目录 1 计数排序 1) 算法思想 2) 代码 3) 时间复杂度与空间复杂度分析 (1) 时间复杂度 (2) 空间复杂度 4) 计…...

高性能Python Web 框架--FastAPI 学习「基础 → 进阶 → 生产级」
以下是针对 FastAPI 的保姆级教程,包含核心概念、完整案例和关键注意事项,采用「基础 → 进阶 → 生产级」的三阶段教学法: 一、FastAPI介绍 FastAPI 是一个现代化的、高性能的 Python Web 框架,专门用于构建 APIs(应…...

Qt QML自定义LIstView
QML ListView组合拳做列表,代码不可直接复制使用,需要小改 先上图看效果 样式1 样式2 样式3 原理:操作:技术点:代码片段: 先上图看效果 样式1 三个表格组合成要给,上下滚动时,三个同时滚动&am…...

C++进阶--红黑树的实现
文章目录 红黑树的实现红黑树的概念红黑树的规则红黑树的效率 红黑树的实现红黑树的结构红黑树的插入变色单旋(变色)双旋(变色) 红黑树的查找红黑树的验证 总结:结语 很高兴和大家见面,给生活加点impetus&a…...

WPF之值转换器
文章目录 目录什么是值转换器IValueConverter接口Convert方法ConvertBack方法 创建和使用值转换器定义转换器类在XAML中使用转换器转换器参数(ConverterParameter) 常用转换器实现布尔值转可见性(BoolToVisibilityConverter)数值转…...

黄金、碳排放期货市场API接口文档
StockTV 提供了多种期货市场的数据接口,包括获取K线图表数据、查询特定期货的实时行情等。以下为对接期货市场的详细接口说明。 一、获取K线图表数据 通过调用/futures/kline接口,您可以获取指定期货合约的历史K线数据(例如开盘价、最高价、…...

云上系统CC攻击如何进行检测与防御?
云上系统遭受CC攻击(Challenge Collapsar,一种针对应用层的DDoS攻击)时,检测与防御需结合流量分析、行为识别和技术手段,以下是核心方法: 一、检测方法 异常流量分析 监控请求量突增&#…...

qml中的TextArea使用QSyntaxHighlighter显示高亮语法
效果图,左侧显示行号,右侧用TextArea显示文本内容,并且语法高亮。 2025年5月8号更新 1、多行文本注释 多行文本注释跟普通的高亮规则代码不太一样,代码需要修改,这里以JavaScript举例。 先制定多行文本注释规则&…...

QuecPython+腾讯云:快速连接腾讯云l0T平台
该模块提供腾讯 IoT 平台物联网套件客户端功能,目前的产品节点类型仅支持“设备”,设备认证方式支持“一机一密”和“动态注册认证”。 BC25PA系列不支持该功能。 初始化腾讯 IoT 平台 TXyun TXyun(productID, devicename, devicePsk, ProductSecret)配置腾讯 IoT…...

RocketMQ 深度解析:架构设计与最佳实践
在分布式系统架构日益复杂的今天,消息中间件作为系统间通信的桥梁,扮演着至关重要的角色。RocketMQ 作为阿里开源的高性能分布式消息中间件,凭借其卓越的性能、丰富的功能以及高可用性,在电商、金融、互联网等众多领域得到广泛应用…...

Transformer编码器+SHAP分析,模型可解释创新表达!
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 基本介绍 基于SHAP分析的特征选择和贡献度计算,Matlab2023b代码实现;基于MATLAB的SHAP可解释Transformer编码器回归模型,敏感性分析方法。 详细介绍 引言 在正向渗透(…...

[特殊字符]适合母亲节的SVG模版[特殊字符]
宝藏模版 往期推荐(点击阅读): 趣味效果|高大上|可爱风|年终总结I|年终总结II|循环特效|情人节I|情人节II|情人节IIII|妇女节I&…...

浅蓝色调风格人像自拍Lr调色预设,手机滤镜PS+Lightroom预设下载!
调色教程 浅蓝色调风格人像自拍 Lr 调色是利用 Adobe Lightroom 软件针对人像自拍照进行后期处理的一种调色方式。它通过对照片的色彩、对比度、亮度等参数进行精细调整,将画面的主色调打造为清新、柔和的浅蓝色系,赋予人像自拍独特的清新、文艺风格&…...

isp流程介绍(yuv格式阶段)
一、前言介绍 前面两章里面,已经分别讲解了在Raw和Rgb域里面,ISP的相关算法流程,从前面文章里面可以看到,在Raw和Rgb域里面,很多ISP算法操作,更像是属于sensor矫正或者说sensor标定操作。本质上来说&#x…...

数巅智能携手北京昇腾创新中心深耕行业大模型应用
当前,AI技术正在加速向各行业深度渗透,成为驱动产业转型和社会经济发展的重要引擎。构建开放协作的AI应用生态体系、推动技术和应用深度融合,已成为行业发展的重要趋势。 近日,数巅智能与北京昇腾人工智能计算中心(北京昇腾创新中…...

【LangChain高级系列】LangGraph第一课
前言 我们今天直接通过一个langgraph的基础案例,来深入探索langgraph的核心概念和工作原理。 基本认识 LangGraph是一个用于构建具有LLMs的有状态、多角色应用程序的库,用于创建代理和多代理工作流。与其他LLM框架相比,它提供了以下核心优…...
简介)
增强学习(Reinforcement Learning)简介
增强学习(Reinforcement Learning)简介 增强学习是机器学习的一种范式,其核心目标是让智能体(Agent)通过与环境的交互,基于试错机制和延迟奖励反馈,学习如何选择最优动作以最大化长期累积回报。…...

常见降维算法分析
一、常见的降维算法 LDA线性判别PCA主成分分析t-sne降维 二、降维算法原理 2.1 LDA 线性判别 原理 :LDA(Linear Discriminant Analysis)线性判别分析是一种有监督的降维方法。它的目标是找到一个投影方向,使得不同类别的数据在…...

计算机二级(C语言)已过
非线性结构:树、图 链表和队列的结构特性不一样,链表可以在任何位置插入、删除,而队列只能在队尾入队、队头出队 对长度为n的线性表排序、在最坏情况下时间复杂度,二分查找为O(log2n),顺序查找为O(n),哈希查…...

2025年3月,韩先超对国网宁夏进行Python线下培训
大家好,我是韩先超!在2025年3月3号和4号,为 宁夏国网 的运维团队进行了一场两天的 Python培训 ,培训目标不仅是让大家学会Python编程,更是希望大家能够通过这门技术解决实际工作中的问题,提升工作效率。 对…...

ATH12K驱动框架架构图
ATH12K驱动框架架构图 ATH12K驱动框架架构图(分层描述)I. 顶层架构II. 核心数据结构层次关系III. 主要模块详解1. 核心模块 (Core)2. 硬件抽象层 (HAL)3. 无线管理接口 (WMI)4. 主机目标通信 (HTC)5. 复制引擎 (CE)6. MAC层7. 数据路径 (DP)IV. 关键数据流路径1. 发送数据流 …...

pcb样板打样厂家哪家好?
国内在PCB样板加工领域具有较强竞争力的企业主要包括以下几家,综合技术实力、市场份额、客户评价及行业认可度进行推荐: 1. 兴森科技 行业地位:国内最大的PCB样板生产商,细分领域龙头企业,月订单品种数可达25,000种&…...

[计算机网络]物理层
文章目录 物理层的概述与功能传输介质双绞线:分类:应用领域: 同轴电缆:分类: 光纤:分类: 无线传输介质:无线电波微波:红外线:激光: 物理层设备中继器(Repeater):放大器:集线器(Hub)&…...

幂等操作及处理措施
利用token模式去避免幂等操作 按以上图所示,除了token,应该也可以把传入的参数用MD5加密,当成key放入redis里面,业务执行完后再删除这个key.如还没有执行完,则请不要重复操作。纯属个人理解...
