【强化学习】动态规划(Dynamic Programming, DP)算法
1、动态规划算法解题
LeetCode 931. 下降路径最小和
给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
1. 自底向上,迭代,dp数组
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();vector<vector<int>> dp(m, vector<int>(n));for (int j=0; j<n; j++){dp[m-1][j] = matrix[m-1][j];}for (int i=m-2; i>=0; i--){for (int j=0; j<n; j++){dp[i][j] = matrix[i][j] + dp[i+1][j];if (j-1 >= 0) dp[i][j] = min(dp[i][j], matrix[i][j] + dp[i+1][j-1]);if (j+1 < n) dp[i][j] = min(dp[i][j], matrix[i][j] + dp[i+1][j+1]);}}int res = INT_MAX;for (int j=0; j<n; j++){res = min(res, dp[0][j]);}return res;}
};
2. 自顶向下,递归,备忘录memo
class Solution {
public:vector<vector<int>> memo;int minFallingPathSum(vector<vector<int>>& matrix) {int res = 99999;int n = matrix.size();memo.resize(n, vector<int>(n, 99999));for (int j = 0; j < n; j++) res = min(res, dp(matrix, n-1, j));return res;}int dp(vector<vector<int>>& matrix, int i, int j){if (i < 0 || j < 0 || i > matrix.size()-1 || j > matrix[0].size()-1)return 66666;// base caseif (i == 0) return matrix[0][j];// 查找备忘录if (memo[i][j] != 99999) return memo[i][j];// 状态转移memo[i][j] = min(min(dp(matrix, i-1, j-1), dp(matrix, i-1, j)), dp(matrix, i-1, j+1)) + matrix[i][j];return memo[i][j];}
};
2、强化学习 - 动态规划算法
动态规划(Dynamic Programming, DP)是强化学习中基于模型(model-based)方法的核心,通过已知的环境模型(状态转移概率和回报函数)利用贝尔曼方程(Bellman Equation)反复计算值函数,从而推导出最优策略。
动态规划方法假设智能体拥有环境的完美模型,即知道在任何状态下采取任何动作所带来的即时奖励以及转移到下一个状态的概率。动态规划主要用于解决强化学习中的“规划”问题,即在已知环境动力学的情况下找到最优策略。
- 在DP框架下:策略评估(Policy Evaluation)与策略改进(Policy Improvement)
- 两大类算法:策略迭代(Policy Iteration)与值迭代(Value Iteration)
2.1. 背景知识
马尔可夫决策过程(MDP)
-
MDP定义:一个MDP由五元组 ( S , A , P , R , γ ) (\mathcal{S}, \mathcal{A}, P, R, \gamma) (S,A,P,R,γ) 构成,其中 S \mathcal{S} S 是状态集合, A \mathcal{A} A 是动作集合, P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a) 是状态转移概率, R ( s , a , s ′ ) R(s,a,s') R(s,a,s′) 是即时回报, γ ∈ [ 0 , 1 ) \gamma\in[0,1) γ∈[0,1) 是折扣因子。
-
值函数:状态价值函数 V π ( s ) V^\pi(s) Vπ(s) 表示在策略 π \pi π 下从状态 s s s 开始获得的期望累积折扣回报;动作价值函数 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a) 则表示在状态 s s s 执行动作 a a a 后执行策略 π \pi π 的期望价值。
2.2. 动态规划原理
动态规划利用已知的MDP模型,基于贝尔曼方程迭代计算值函数,并根据值函数更新策略,直至收敛到最优策略。
1. 策略评估(Policy Evaluation)
策略评估的目标是在给定策略 π \pi π 下,反复应用贝尔曼期望方程
V k + 1 ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r P ( s ′ , r ∣ s , a ) [ r + γ V k ( s ′ ) ] V_{k+1}(s) = \sum_{a}\pi(a|s)\sum_{s',r}P(s',r|s,a)\bigl[r + \gamma V_k(s')\bigr] Vk+1(s)=a∑π(a∣s)s′,r∑P(s′,r∣s,a)[r+γVk(s′)]
直至 ∥ V k + 1 − V k ∥ ∞ < θ \|V_{k+1} - V_k\|_\infty < \theta ∥Vk+1−Vk∥∞<θ(阈值)
- 符号说明:
- π ( a ∣ s ) \pi(a|s) π(a∣s):策略 π \pi π在状态 s s s下选择动作 a a a的概率。
- r ( s , a ) r(s,a) r(s,a):在状态 s s s采取动作 a a a的即时奖励。
- γ \gamma γ:折扣因子( 0 ≤ γ ≤ 1 0 \leq \gamma \leq 1 0≤γ≤1),表示未来奖励的权重。
- P ( s ′ , r ∣ s , a ) P(s',r|s,a) P(s′,r∣s,a):状态转移概率,表示在状态 s s s采取动作 a a a后转移到状态 s ′ s' s′、获得及时奖励 r r r的概率。
- V k ( s ′ ) V_k(s') Vk(s′):下一状态 s ′ s' s′的值函数。
2. 策略迭代(Policy Iteration)
-
初始化:任意初始化策略 π 0 \pi_0 π0 和相应的 V ( s ) V(s) V(s)。
-
策略评估:对当前策略 π k \pi_k πk 执行上述策略评估,获得 V π k V^{\pi_k} Vπk。
-
策略改进:对所有状态 s s s,更新策略
π k + 1 ( s ) = arg max a ∑ s ′ , r P ( s ′ , r ∣ s , a ) [ r + γ V π k ( s ′ ) ] . \pi_{k+1}(s) = \arg\max_a \sum_{s',r} P(s',r|s,a)\bigl[r + \gamma V^{\pi_k}(s')\bigr]. πk+1(s)=argamaxs′,r∑P(s′,r∣s,a)[r+γVπk(s′)].
-
重复 步骤 2–3,直到策略不再改变。
该算法保证在有限步数内收敛到最优策略 π ∗ \pi^* π∗.
3. 值迭代(Value Iteration)
值迭代将策略评估与策略改进合并:
V k + 1 ( s ) = max a ∑ s ′ , r P ( s ′ , r ∣ s , a ) [ r + γ V k ( s ′ ) ] , V_{k+1}(s) = \max_{a}\sum_{s',r}P(s',r|s,a)\bigl[r + \gamma V_k(s')\bigr], Vk+1(s)=amaxs′,r∑P(s′,r∣s,a)[r+γVk(s′)],
直至 ∥ V k + 1 − V k ∥ ∞ < θ \|V_{k+1} - V_k\|_\infty < \theta ∥Vk+1−Vk∥∞<θ,然后由最终的 V ∗ V^* V∗ 直接提取最优策略:
π ∗ ( s ) = arg max a ∑ s ′ , r P ( s ′ , r ∣ s , a ) [ r + γ V ∗ ( s ′ ) ] \pi^*(s)=\arg\max_a\sum_{s',r}P(s',r|s,a)[r+\gamma V^*(s')] π∗(s)=argamaxs′,r∑P(s′,r∣s,a)[r+γV∗(s′)]
实现步骤
算法伪代码
输入:MDP模型 (S, A, P, R, γ), 收敛阈值 θ
输出:最优策略 π*, 最优值函数 V*1. 初始化 V(s) 任意;π(s) 任意
2. 重复:a. Δ ← 0b. 对于每个状态 s ∈ S:v ← V(s)V(s) ← max_a ∑_{s',r} P(s',r|s,a)[ r + γ V(s') ]Δ ← max(Δ, |v - V(s)|)c. 直到 Δ < θ
3. 对于每个 s ∈ S:π(s) ← argmax_a ∑_{s',r} P(s',r|s,a)[ r + γ V(s') ]
4. 返回 π, V
上述即为值迭代的核心伪代码,策略迭代只需将步骤 2b 中“max”替换为按当前π评估,并在评估后插入策略改进步骤。
Python 实现示例
def value_iteration(P, R, gamma=0.9, theta=1e-6):"""P: dict, P[s][a] = list of (prob, next_s, reward)R: dict, immediate rewards R[s][a][s']"""V = {s: 0.0 for s in P}while True:delta = 0for s in P:v_old = V[s]V[s] = max(sum(prob * (r + gamma * V[s_next])for prob, s_next, r in P[s][a])for a in P[s])delta = max(delta, abs(v_old - V[s]))if delta < theta:break# 策略提取policy = {}for s in P:policy[s] = max(P[s].keys(),key=lambda a: sum(prob * (r + gamma * V[s_next])for prob, s_next, r in P[s][a]))return policy, V
注意事项
- 收敛性:DP方法在折扣因子 γ < 1 \gamma<1 γ<1 或有终止状态的有限MDP中保证收敛。
- 计算复杂度:状态-动作空间过大(例如上百维状态)时,DP算法不可行,需要采用抽样或函数逼近方法(如TD、DQN等)。
- 异步DP:可采用异步更新(Asynchronous DP)和广义策略迭代(Generalized Policy Iteration)以提升效率。
相关文章:
算法)
【强化学习】动态规划(Dynamic Programming, DP)算法
1、动态规划算法解题 LeetCode 931. 下降路径最小和 给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。 下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选…...
uniapp-商城-47-后台 分类数据的生成(通过数据)
在第46章节中,我们为后台数据创建了分类的数据表结构schema,使得可以通过后台添加数据并保存,同时使用云函数进行数据库数据的读取。文章详细介绍了如何通过前端代码实现分类管理功能,包括获取数据、添加、更新和删除分类。主要代…...

java-----------------多态
多态,当前指的是 java 所呈现出来的一个对象 多态 定义 多态是指同一个行为具有多个不同表现形式或形态的能力。在面向对象编程中,多态通过方法重载和方法重写来实现。 强弱类型语言 javascript 或者python 是弱类型语言 C 语言,或者 C…...

【文档智能】开源的阅读顺序(Layoutreader)模型使用指南
一年前,笔者基于开源了一个阅读顺序模型(《【文档智能】符合人类阅读顺序的文档模型-LayoutReader及非官方权重开源》), PDF解析并结构化技术路线方案及思路,文档智能专栏 阅读顺序检测旨在捕获人类读者能够自然理解的…...

Java中的内部类详解
目录 什么是内部类? 生活中的内部类例子 为什么需要内部类? 生活中的例子 内部类的存在意义 内部类的分类 1. 成员内部类 什么是成员内部类? 成员内部类的特点 如何使用成员内部类? 成员内部类访问外部类同名成员 2. …...

Java大师成长计划之第16天:高级并发工具类
📢 友情提示: 本文由银河易创AI(https://ai.eaigx.com)平台gpt-4o-mini模型辅助创作完成,旨在提供灵感参考与技术分享,文中关键数据、代码与结论建议通过官方渠道验证。 在现代Java应用中,处理并…...

lambda 表达式
C 的 lambda 表达式 是一种轻量、内联的函数对象写法,广泛用于标准算法、自定义回调、事件响应等场景。它简洁且强大。以下将系统、详细地讲解 lambda 的语法、捕获规则、应用技巧和实际使用场景。 🧠 一、基本语法 [捕获列表](参数列表) -> 返回类型…...

Edu教育邮箱申请2025年5月
各位好,这里是aigc创意人竹相左边 如你所见,这里是第3部分 现在是选择大学的学科专业 选专业的时候记得考虑一下当前的时间日期。 比如现在是夏天,所以你选秋天入学是合理的。...

JVM内存模型深度解剖:分代策略、元空间与GC调优实战
堆 堆是Java虚拟机(JVM)内存管理的核心区域,其物理存储可能分散于不同内存页,但逻辑上被视为连续的线性空间。作为JVM启动时创建的第一个内存区域,堆承载着几乎所有的对象实例和数组对象(极少数通过逃逸分…...

STM32-TIM定时中断(6)
目录 一、TIM介绍 1、TIM简介 2、定时器类型 3、基本定时器 4、通用定时器 5、定时中断基本结构 6、时基单元的时序 (1)预分频器时序 (2)计数器时序 7、RCC时钟树 二、定时器输出比较功能(PWM) …...

微信小程序地图缩放scale隐性bug
bug1 在真机环境下通过this.mapCtx.getScale获取当前地图的缩放等级带小数, 当设置scale带小数时,地图会先执行到缩放到带小数的缩放等级,然后会再次缩放取整的缩放等级(具体向上取整还是向下取整未知,两种情况都观察…...

window 显示驱动开发-配置内存段类型
视频内存管理器(VidMm)和显示硬件仅支持某些类型的内存段。 因此,内核模式显示微型端口驱动程序(KMD)只能配置这些类型的段。 KMD 可以配置内存空间段和光圈空间段,其中不同: 内存空间段由保存…...

Modbus RTU 详解 + FreeMODBUS移植(附项目源码)
文章目录 前言一、Modbus RTU1.1 通信方式1.2 模式特点1.3 数据模型1.4 常用功能码说明1.5 异常响应码1.6 通信帧格式1.6.1 示例一:读取保持寄存器(功能码 0x03)1.6.2 示例二:写单个线圈(功能码 0x05)1.6.3…...
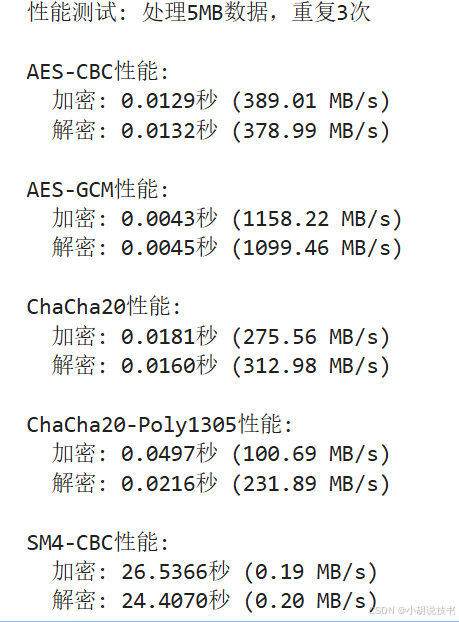
对称加密算法(AES、ChaCha20和SM4)Python实现——密码学基础(Python出现No module named “Crypto” 解决方案)
文章目录 一、对称加密算法基础1.1 对称加密算法的基本原理1.2 对称加密的主要工作模式 二、AES加密算法详解2.1 AES基本介绍2.2 AES加密过程2.3 Python中实现AES加密Python出现No module named “Crypto” 解决方案 2.4 AES的安全考量 三、ChaCha20加密算法3.1 ChaCha20基本介…...

JWT原理及工作流程详解
JSON Web Token(JWT)是一种开放标准(RFC 7519),用于在各方之间安全传输信息。其核心原理是通过结构化、签名或加密的JSON对象实现无状态身份验证和授权。以下是JWT的工作原理和关键组成部分: 1. JWT结构 J…...

【软件设计师:存储】16.计算机存储系统
一、主存储器 存储器是计算机系统中的记忆设备,用来存放程序和数据。 计算机中全部信息,包括输入的原始数据、计算机程序、中间运 行结果和最终运行结果都保存在存储器中。 存储器分为: 寄存器Cache(高速缓冲存储器)主存储器辅存储器一、存储器的存取方式 二、存储器的性…...

【Part 2安卓原生360°VR播放器开发实战】第三节|实现VR视频播放与时间轴同步控制
《VR 360全景视频开发》专栏 将带你深入探索从全景视频制作到Unity眼镜端应用开发的全流程技术。专栏内容涵盖安卓原生VR播放器开发、Unity VR视频渲染与手势交互、360全景视频制作与优化,以及高分辨率视频性能优化等实战技巧。 📝 希望通过这个专栏&am…...

WebRTC通信原理与流程
1、服务器与协议相关 1.1 STUN服务器 图1.1.1 STUN服务器在通信中的位置图 1.1.1 STUN服务简介 STUN(Session Traversal Utilities for NAT,NAT会话穿越应用程序)是一种网络协议,它允许位于NAT(或多重 NAT)…...

Java版ERP管理系统源码(springboot+VUE+Uniapp)
ERP系统是企业资源计划(Enterprise Resource Planning)系统的缩写,它是一种集成的软件解决方案,用于协调和管理企业内各种关键业务流程和功能,如财务、供应链、生产、人力资源等。它的目标是帮助企业实现资源的高效利用…...

Redis总结(六)redis持久化
本文将简单介绍redis持久化的两种方式 redis提供了两种不同级别的持久化方式: RDB持久化方式能够在指定的时间间隔能对你的数据进行快照存储.AOF持久化方式记录每次对服务器写的操作,当服务器重启的时候会重新执行这些命令来恢复原始的数据,AOF命令以redis协议追加保…...

使用FastAPI微服务在AWS EKS中构建上下文增强型AI问答系统
系统概述 本文介绍如何使用FastAPI在AWS Elastic Kubernetes Service (EKS)上构建一个由多个微服务组成的AI问答系统。该系统能够接收用户输入的提示(prompt),通过调用其他微服务从AWS ElastiCache on Redis和Amazon DynamoDB获取相关上下文,然后利用AW…...

PMIC电源管理模块的PCB设计
目录 PMU模块简介 PMU的PCB设计 PMU模块简介 PMIC(电源管理集成电路)是现代电子设备的核心模块,负责高效协调多路电源的转换、分配与监控。它通过集成DC-DC降压/升压、LDO线性稳压、电池充电管理、功耗状态切换等功能,替代传统分…...

正大视角下的结构交易节奏:如何借助数据捕捉关键转折
正大视角下的结构交易节奏:如何借助数据捕捉关键转折 在日常的交易结构研究中,节奏与分型常常被误解为“预测工具”,实则更应作为状态识别的参考。正大团队在模型演化过程中提出了“节奏-结构对齐”的分析方式,通过数据驱动来判断…...

华为云Flexus+DeepSeek征文|DeepSeek-V3商用服务开通教程
目录 DeepSeek-V3/R1商用服务开通使用感受 DeepSeek-V3/R1商用服务开通 1、首先需要访问ModelArts Studio_MaaS_大模型即服务_华为云 2、在网站右上角登陆自己的华为云账号,如果没有华为云账号的话,则需要自己先注册一个。 3、接着点击ModelArts Stu…...

STM32F103RC中ADC1和ADC2通道复用
以下是STM32F103RC中ADC1和ADC2通道复用的示意图及文字说明,帮助直观理解这种共享关系: ADC1/ADC2引脚复用示意图 GPIO引脚 ADC1通道 ADC2通道 ┌─────────┐ ┌─────────┐ ┌─────────┐ │ PA0 ├─…...

Qt—鼠标移动事件的趣味小程序:会移动的按钮
1.项目目标 本次根据Qt的鼠标移动事件实现一个趣味小程序:当鼠标移动到按钮时,按钮就会随机出现在置,以至于根本点击不到按钮。 2.项目步骤 首先现在ui界面设计控件(也可以用代码的方式创建,就不多说了) 第一个按钮不需…...

鞋样设计软件
Sxy 64鞋样设计软件是一款专业级鞋类设计工具 专为鞋业设计师与制鞋企业开发 该软件提供全面的鞋样设计功能 包括二维开版 三维建模 放码排料等核心模块 支持从草图构思到成品输出的完整设计流程 内置丰富的鞋型数据库与部件库 可快速生成各种鞋款模板 软件采用智能放码技术 精…...

LeRobot 项目部署运行逻辑(六)——visualize_dataset_html.py/visualize_dataset.py
可视化脚本包括了两个方法:远程下载 huggingface 上的数据集和使用本地数据集 脚本主要使用两个: 目前来说,ACT 采集训练用的是统一时间长度的数据集,此外,这两个脚本最大的问题在于不能裁剪,这也是比较好…...

Windows Server 2025开启GPU分区(GPU-P)部署DoraCloud云桌面
本文描述在ShareStation工作站虚拟化方案的部署过程。 将服务器上部署 Windows Server、DoraCloud,并创建带有vGPU的虚拟桌面。 GPU分区技术介绍 GPU-P(GPU Partitioning) 是微软在 Windows 虚拟化平台(如 Hyper-V)中…...
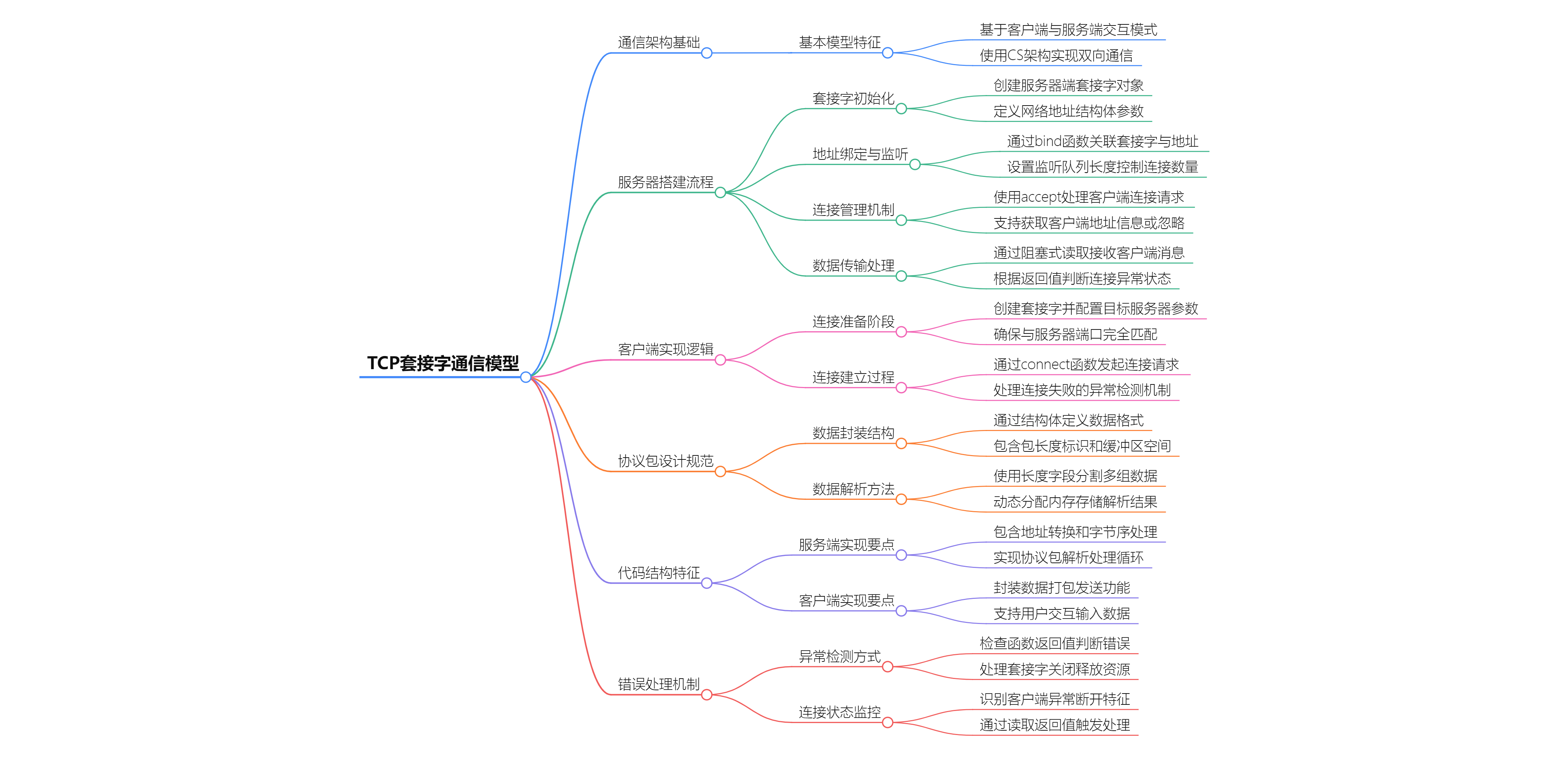
TCP套接字通信核心要点
TCP套接字通信核心要点 通信模型架构 客户端-服务端模型 CS架构:客户端发起请求,服务端响应和处理请求双向通道:建立连接后实现全双工通信 服务端搭建流程 核心步骤 创建套接字 int server socket(AF_INET, SOCK_STREAM, 0); 参数说明&am…...
