STM32实现九轴IMU的卡尔曼滤波
在嵌入式系统中,精确的姿态估计对于无人机、机器人和虚拟现实等应用至关重要。九轴惯性测量单元(IMU)通过三轴加速度计、陀螺仪和磁力计提供全面的运动数据。然而,这些传感器数据常伴随噪声和漂移,单独使用无法满足高精度需求。卡尔曼滤波作为一种强大的传感器融合算法,能够有效结合多传感器数据,估计系统状态。

九轴IMU通常由以下三部分组成:
- 三轴加速度计:测量线性加速度,可用于确定重力方向和线性运动
- 三轴陀螺仪:测量角速度,用于检测旋转运动
- 三轴磁力计:测量地磁场,提供绝对方向参考
这些传感器的互补特性使得传感器融合成为必要。融合算法通过结合各传感器数据,克服单一传感器的局限性,提供更准确的姿态估计。

由于各传感器存在固有缺陷(如陀螺仪漂移、加速度计噪声、磁力计干扰),单独使用无法提供可靠的姿态估计。传感器融合通过数学模型整合多传感器数据,生成更精确的估计结果。常用的融合算法包括互补滤波和卡尔曼滤波,其中卡尔曼滤波因其理论最优性广泛应用于姿态估计。
卡尔曼滤波是一种递归算法,用于从噪声测量中估计动态系统的状态。它假设系统是线性的,噪声为高斯分布。卡尔曼滤波包括两个主要步骤:
- 预测步骤:根据系统模型预测下一时刻的状态和协方差。
- 更新步骤:利用新测量值修正预测状态,计算卡尔曼增益以平衡预测和测量。
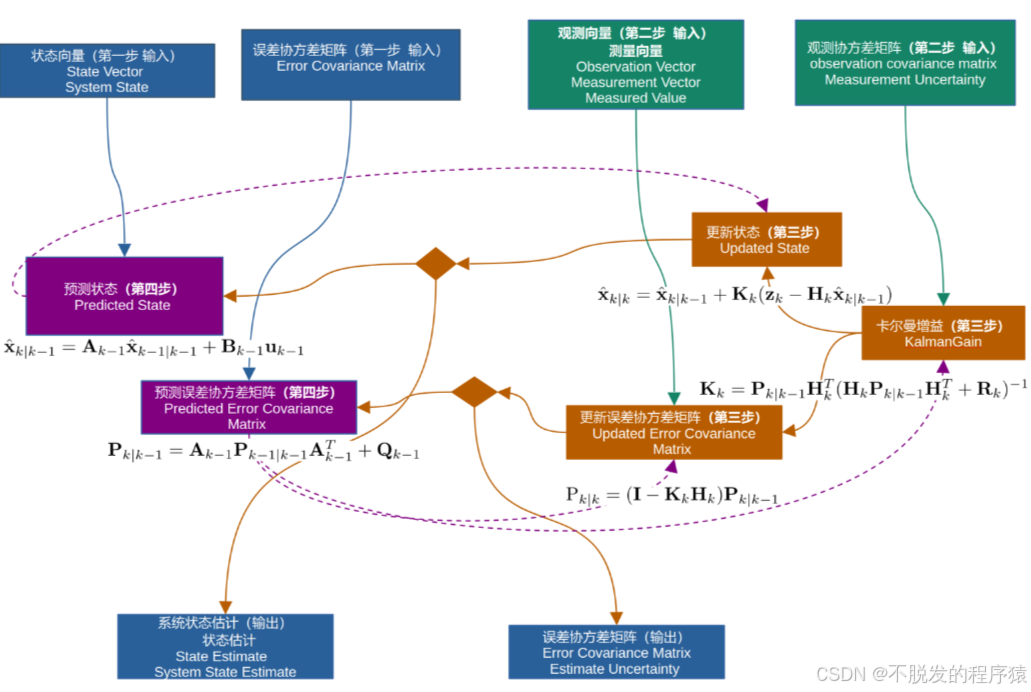
对于卡尔曼滤波的原理,我们不再细究,网上有很多资料,本篇文章主要讲解嵌入式工程师如何使用代码实现卡尔曼滤波。
在STM32微控制器上实现九轴IMU的卡尔曼滤波需要选择一款支持浮点运算单元(FPU)的STM32微控制器(如STM32F4系列),以高效处理矩阵运算。将九轴IMU(如MPU9250)通过I2C或SPI接口连接到STM32开发板。确保电源稳定,通信线路正确连接。
以下是九轴IMU卡尔曼滤波的核心实现:
// 状态向量:[q0, q1, q2, q3, bgx, bgy, bgz]
float state[7];// 状态协方差矩阵 P (7x7)
float P[49];// 过程噪声协方差矩阵 Q (7x7)
float Q[49];// 观测噪声协方差矩阵 R (6x6):3个加速度计和3个磁力计
float R[36];// 状态转换矩阵 F (7x7)
float F[49];// 观测矩阵 H (6x7)
float H[42];// 卡尔曼增益 K (7x6)
float K[42];// 预测状态
float state_pred[7];// 预测协方差
float P_pred[49];// 残差
float y[6];// S = H*P*H^T + R
float S[36];// 初始状态
void init_state(float initial_q[4], float initial_bg[3]) {// 初始化状态向量memcpy(state, initial_q, 4*sizeof(float));memcpy(state+4, initial_bg, 3*sizeof(float));// 初始化协方差矩阵 Pmemset(P, 0, 49*sizeof(float));P[0] = 0.01f; P[7] = 0.01f; P[14] = 0.01f; P[21] = 0.01f; // q的方差P[28] = 0.01f; P[35] = 0.01f; P[42] = 0.01f; // bg的方差// 初始化过程噪声协方差 Qmemset(Q, 0, 49*sizeof(float));Q[0] = 0.001f; Q[7] = 0.001f; Q[14] = 0.001f; Q[21] = 0.001f; // q的噪声Q[28] = 0.0001f; Q[35] = 0.0001f; Q[42] = 0.0001f; // bg的噪声// 初始化观测噪声协方差 Rmemset(R, 0, 36*sizeof(float));R[0] = 0.1f; R[7] = 0.1f; R[14] = 0.1f; // 加速度计噪声R[21] = 0.1f; R[28] = 0.1f; R[35] = 0.1f; // 磁力计噪声
}// 预测步骤
void predict(float gyro[3], float dt) {// 计算角速度四元数float omega[4] = {0, gyro[0], gyro[1], gyro[2]};float theta = sqrt(omega[1]*omega[1] + omega[2]*omega[2] + omega[3]*omega[3]) * dt;float axis[3];if (theta > 1e-6) {axis[0] = omega[1]/theta;axis[1] = omega[2]/theta;axis[2] = omega[3]/theta;} else {axis[0] = 0;axis[1] = 0;axis[2] = 0;}float dq[4] = {cos(theta/2), axis[0]*sin(theta/2), axis[1]*sin(theta/2), axis[2]*sin(theta/2)};// 预测四元数float q[4];quaternion_multiply(state, dq, q);quaternion_normalize(q);memcpy(state_pred, q, 4*sizeof(float));// 陀螺仪偏置保持不变memcpy(state_pred+4, state+4, 3*sizeof(float));// 计算状态转换矩阵 F// (这里简化为恒等矩阵,实际应用中需要正确计算)memset(F, 0, 49*sizeof(float));for(int i=0; i<7; i++) F[i*8] = 1.0f;// P_pred = F*P*F^T + G*Q*G^T// (这里简化为P_pred = P + Q)for(int i=0; i<49; i++) P_pred[i] = P[i] + Q[i];// 更新状态和协方差memcpy(state, state_pred, 7*sizeof(float));memcpy(P, P_pred, 49*sizeof(float));
}// 更新步骤
void update(float acc[3], float mag[3], float ref_mag[3]) {// 计算期望的加速度计测量值float q_inv[4];quaternion_conjugate(state, q_inv);float expected_acc[4] = {0, 0, 0, -1};quaternion_multiply(state, expected_acc, expected_acc);quaternion_multiply(expected_acc, q_inv, expected_acc);expected_acc[1] /= expected_acc[0];expected_acc[2] /= expected_acc[0];expected_acc[3] /= expected_acc[0];// 计算期望的磁力计测量值float expected_mag[4];quaternion_multiply(state, ref_mag, expected_mag);quaternion_multiply(expected_mag, q_inv, expected_mag);expected_mag[1] /= expected_mag[0];expected_mag[2] /= expected_mag[0];expected_mag[3] /= expected_mag[0];// 组合观测向量float z[6] = {acc[0], acc[1], acc[2],mag[0], mag[1], mag[2]};float h[6] = {expected_acc[1], expected_acc[2], expected_acc[3],expected_mag[1], expected_mag[2], expected_mag[3]};// 计算残差for(int i=0; i<6; i++) y[i] = z[i] - h[i];// 计算观测矩阵 H// (这里简化为恒等矩阵,实际应用中需要正确计算)memset(H, 0, 42*sizeof(float));for(int i=0; i<6; i++) H[i*8 + i] = 1.0f;// 计算 S = H*P*H^T + R// (这里简化为 S = H*P*H^T + R)memset(S, 0, 36*sizeof(float));for(int i=0; i<6; i++) {for(int j=0; j<7; j++) {if (H[i*7 + j] == 0) continue;for(int k=0; k<6; k++) {if (H[k*7 + j] == 0) continue;S[i*6 + k] += H[i*7 + j] * P[j*7 + k] * H[k*7 + j];}}}for(int i=0; i<36; i++) S[i] += R[i];// 计算卡尔曼增益 K = P*H^T*S^{-1}// (这里简化为 K = P*H^T / (H*P*H^T + R))memset(K, 0, 42*sizeof(float));for(int i=0; i<7; i++) {for(int j=0; j<6; j++) {float sum = 0;for(int k=0; k<7; k++) {sum += P[i*7 + k] * H[j*7 + k];}K[i*6 + j] = sum / S[j*6 + j];}}// 更新状态for(int i=0; i<7; i++) {float sum = 0;for(int j=0; j<6; j++) {sum += K[i*6 + j] * y[j];}state[i] += sum;}// 更新协方差memset(P, 0, 49*sizeof(float));for(int i=0; i<7; i++) {for(int j=0; j<7; j++) {float sum = 0;for(int k=0; k<6; k++) {sum += K[i*6 + k] * H[k*7 + j];}P[i*7 + j] = (1 - sum) * P_pred[i*7 + j];}}
}
以下是完整的STM32实现框架:
#include "stm32f10x.h"// 定义MPU9250和HMC5883L的I2C地址
#define MPU9250_ADDR 0x68
#define HMC5883L_ADDR 0x1E// MPU9250寄存器定义
#define PWR_MGMT_1 0x6B
#define SMPLRT_DIV 0x19
#define CONFIG 0x1A
#define GYRO_CONFIG 0x1B
#define ACCEL_CONFIG 0x1C
#define INT_ENABLE 0x38
#define PWR_MGMT_2 0x3B// HMC5883L寄存器定义
#define HMC5883L_CTRL_REG_A 0x0A
#define HMC5883L_CTRL_REG_B 0x0B// 状态向量:[q0, q1, q2, q3, bgx, bgy, bgz]
float state[7];// 状态协方差矩阵 P (7x7)
float P[49];// ... 其他变量声明// I2C写操作
void i2c_write(uint8_t addr, uint8_t reg, uint8_t value) {// 实现I2C写操作
}// I2C读操作
uint8_t i2c_read(uint8_t addr, uint8_t reg) {// 实现I2C读操作
}// 四元数乘法
void quaternion_multiply(float *q1, float *q2, float *result) {// 实现四元数乘法
}// 四元数归一化
void quaternion_normalize(float *q) {// 实现四元数归一化
}// 四元数共轭
void quaternion_conjugate(float *q, float *result) {// 实现四元数共轭
}// MPU9250初始化
void mpu9250_init(void) {// 实现MPU9250初始化
}// 从MPU9250读取加速度计数据
void read_accel(float *accel) {// 从MPU9250读取加速度计数据
}// 从MPU9250读取陀螺仪数据
void read_gyro(float *gyro) {// 从MPU9250读取陀螺仪数据
}// 从HMC5883L读取磁力计数据
void read_magnet(float *magnet) {// 从HMC5883L读取磁力计数据
}// 初始化卡尔曼滤波器
void init_kalman(float initial_q[4], float initial_bg[3]) {// 初始化卡尔曼滤波器
}// 卡尔曼滤波预测步骤
void kalman_predict(float gyro[3], float dt) {// 实现卡尔曼滤波预测步骤
}// 卡尔曼滤波更新步骤
void kalman_update(float accel[3], float magnet[3], float ref_magnet[3]) {// 实现卡尔曼滤波更新步骤
}int main(void) {// 初始化STM32外设// ...// 初始化MPU9250mpu9250_init();// 初始化卡尔曼滤波器float initial_q[4] = {1, 0, 0, 0}; // 初始姿态为0角度float initial_bg[3] = {0, 0, 0}; // 初始陀螺仪偏置为0init_kalman(initial_q, initial_bg);// 参考地磁场值(根据实际位置确定)float ref_magnet[3] = {0, 0, -1}; // 南极指向地心float gyro[3], accel[3], magnet[3];while(1) {// 读取传感器数据read_gyro(gyro);read_accel(accel);read_magnet(magnet);// 预测步骤float dt = 0.01; // 10ms采样周期kalman_predict(gyro, dt);// 更新步骤kalman_update(accel, magnet, ref_magnet);// 处理滤波结果// ...// 延时Delay_Ms(10);}
}
如果不想自己手写代码,可以使用STMicroelectronics的MotionFX库。
它是X-CUBE-MEMS1软件扩展的一部分,内置优化的卡尔曼滤波算法,支持6轴和9轴IMU融合。该库针对STM32微控制器优化,适合快速开发。
MotionFX库在不同STM32平台上的性能效果如下:
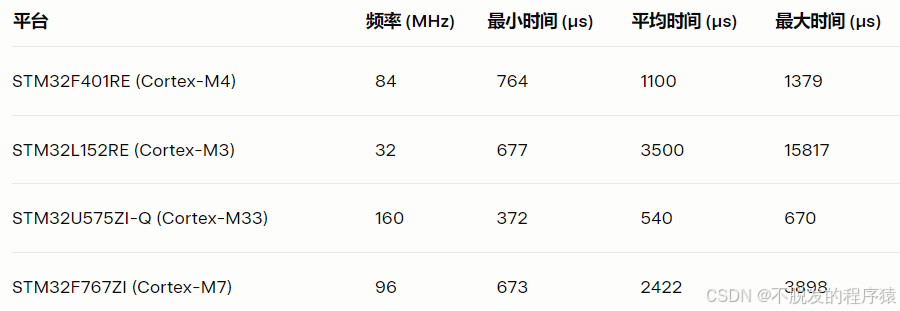
在STM32上实现九轴IMU的卡尔曼滤波是嵌入式系统中实现高精度姿态估计的有效方法。通过理解IMU的工作原理、卡尔曼滤波的理论以及系统建模,开发者可以从头实现EKF算法。或者,利用ST的MotionFX库可以显著简化开发流程,同时保持高性能。
相关文章:

STM32实现九轴IMU的卡尔曼滤波
在嵌入式系统中,精确的姿态估计对于无人机、机器人和虚拟现实等应用至关重要。九轴惯性测量单元(IMU)通过三轴加速度计、陀螺仪和磁力计提供全面的运动数据。然而,这些传感器数据常伴随噪声和漂移,单独使用无法满足高精…...

机器学习-简要与数据集加载
一.机器学习简要 1.1 概念 机器学习即计算机在数据中总结规律并预测未来结果,这一过程仿照人类的学习过程进行。 深度学习是机器学习中的重要算法的其中之一,是一种偏近现代的算法。 1.2 机器学习发展历史 从上世纪50年代的图灵测试提出、塞缪尔开发…...
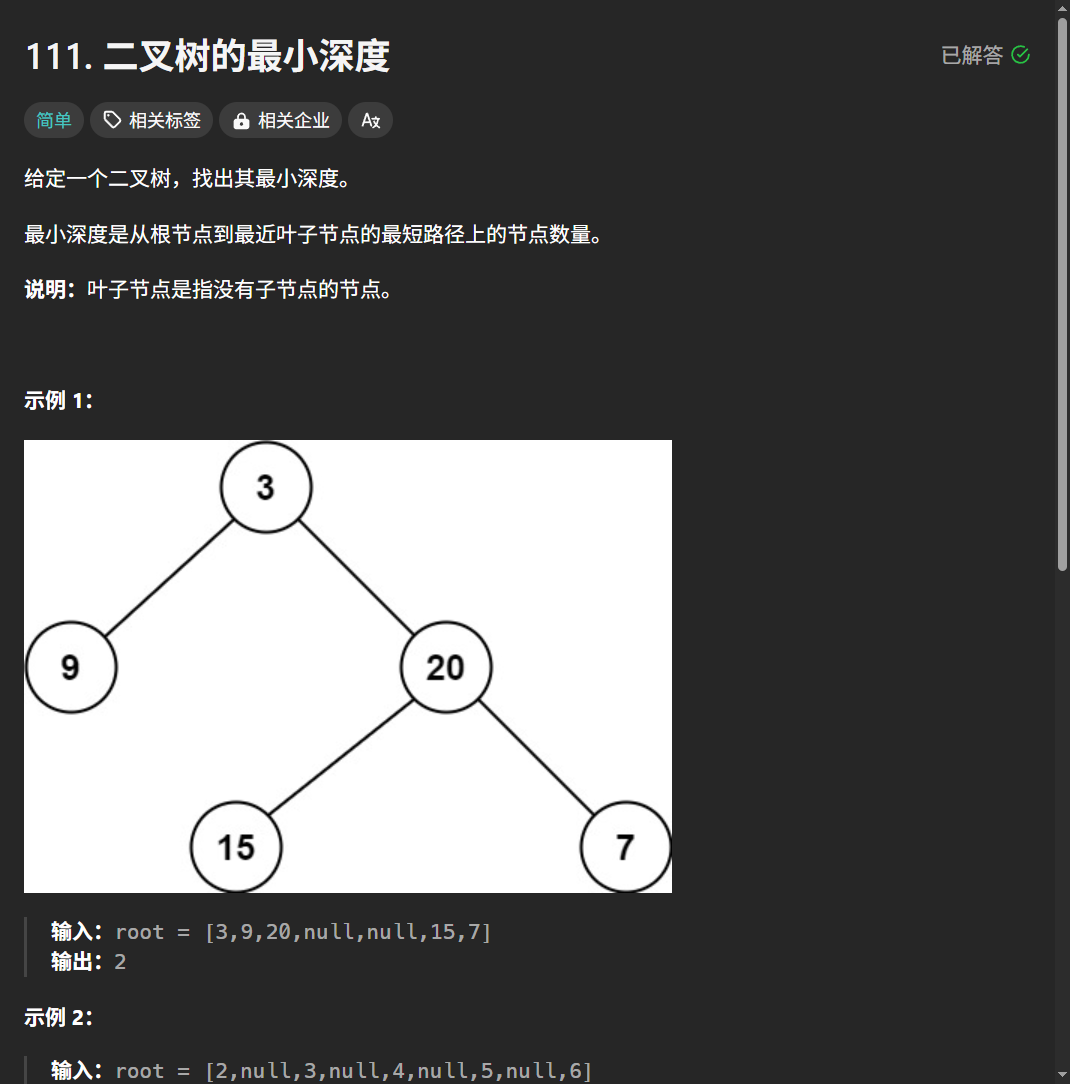
算法训练营第十三天|226.翻转二叉树、101. 对称二叉树、 104.二叉树的最大深度、111.二叉树的最小深度
递归 递归三部曲: 1.确定参数和返回值2.确定终止条件3.确定单层逻辑 226.翻转二叉树 题目 思路与解法 第一想法: 递归,对每个结点进行反转 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, le…...
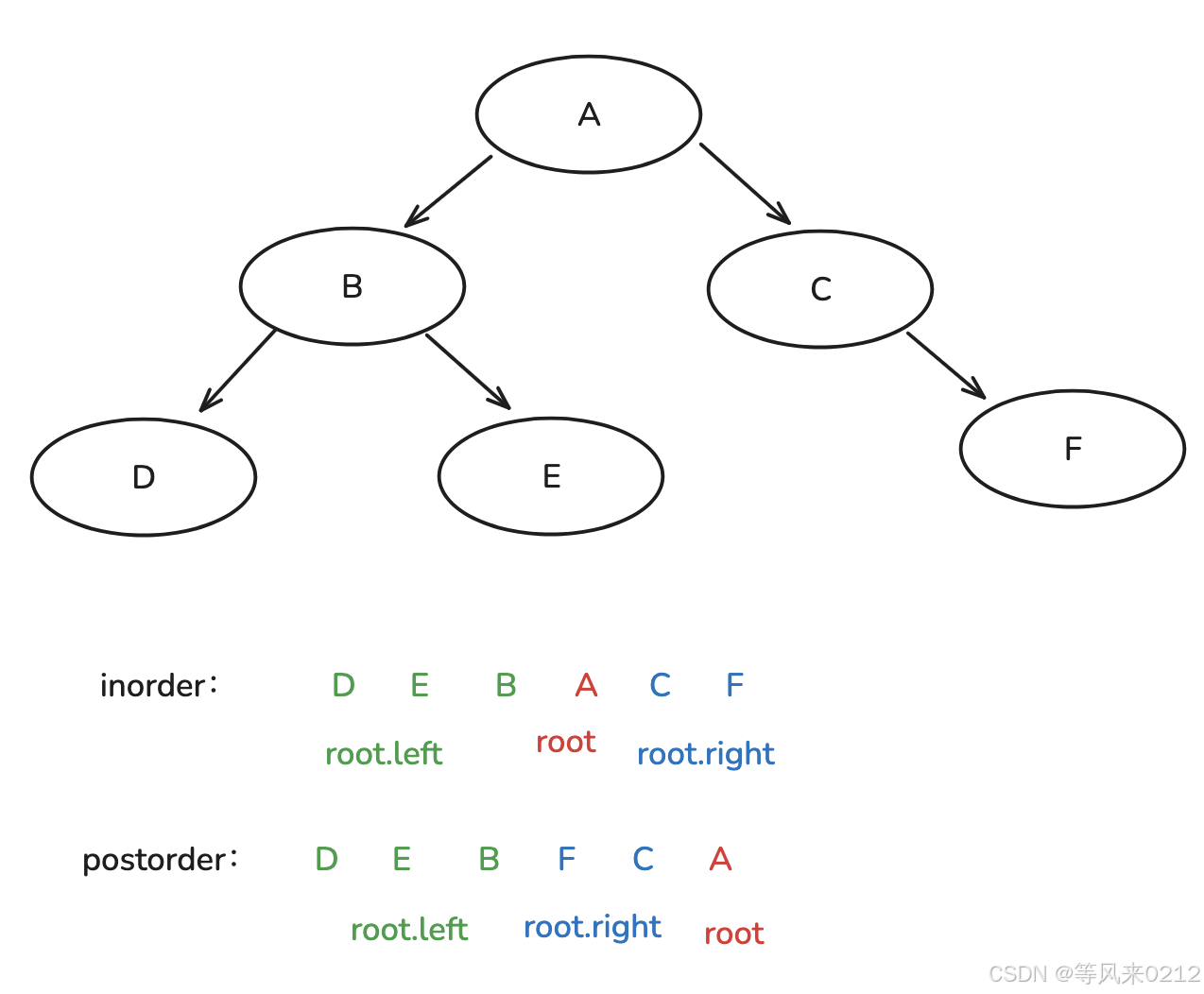
二叉树的遍历与构造
好想回家,我想回家跟馒头酱玩,想老爸老妈。如果上天再给我一次选择的机会,我会选择当一只小动物,或者当棵大树也好,或者我希望自己不要有那么多多余的情绪,不要太被别人影响,开心点,…...

Python+OpenCV实现手势识别与动作捕捉:技术解析与应用探索
引言:人机交互的新维度 在人工智能与计算机视觉技术飞速发展的今天,手势识别与动作捕捉技术正逐步从实验室走向大众生活。通过Python的OpenCV库及MediaPipe等工具,开发者能够以较低门槛实现精准的手部动作识别,为虚拟现实、智能家…...

MYSQL服务的使用流程
MYSQL是一个单进程多线程,支持多用户,基于客户机/服务器的关系数据库管理系统。与其他数据库管理系统相比,MYSQL具有体积小,易于安装,运行速度快,功能齐全,成本低廉以及开源等特点。MYSQL可运行…...

华为云API、SDK是什么意思?有什么区别和联系?
目录 一、API:像菜单 + 打电话点餐 📌 本质解释: 🔧 操作方式(偏底层): 🍱 类比举例: 二、SDK:像外卖App(美团/饿了么)自动点餐 📌 本质解释: 🔧 操作方式(偏上层): 🍱 类比举例: 三、联系:SDK 是对 API 的“封装与简化” 四、操作实例对…...

【java】使用iText实现pdf文件增加水印功能
maven依赖 <dependencies><dependency><groupId>com.itextpdf</groupId><artifactId>itext7-core</artifactId><version>7.2.5</version><type>pom</type></dependency> </dependencies>实现代码 前…...

Python爬虫实战:获取艺恩娱数最新电影舆情数据并分析,为影院排片做参考
一、引言 在电影行业蓬勃发展的当下,了解影片的各项指数对于票房宣发排片起着至关重要的作用。艺恩娱数网站作为电影行业重要的数据平台,提供了丰富且有价值的电影相关数据。然而,直接从该网站获取数据面临诸多挑战。Python 作为一种功能强大、应用广泛的编程语言,拥有众多…...

Linux指令入门:DevOps与SRE视角
文章目录 Linux指令入门:DevOps与SRE视角一、Linux基础命令概述二、文件系统操作命令1. 文件与目录基本操作2. 文件查看与编辑3. 文件压缩与归档 三、进程管理命令1. 进程查看与控制2. 服务管理(Systemd) 四、网络管理命令1. 网络连接与诊断2…...

socket套接字-TCP
上一篇:socket套接字-UDP(下)https://blog.csdn.net/Small_entreprene/article/details/147569071?fromshareblogdetail&sharetypeblogdetail&sharerId147569071&sharereferPC&sharesourceSmall_entreprene&sharefromfr…...

Ctrl + D是如何与内核文件结束符对应的?如何模拟文件结束符?数字中间为什么不能插入空格或逗号?丰富多彩的语句结束符或分隔符?语句结束符?
目录 Ctrl D是如何与内核文件结束符对应的? 如何模拟文件结束符? 哪些编程语言支持数值中插入分隔符更容易看清楚? 下划线分隔符 数字中间为什么不能插入空格或逗号? 丰富多彩的语句结束符或分隔符 误用分号 语句结束符 不同语言的结束符 更改语句结束符 Ctrl …...

MiM: Mask in Mask Self-SupervisedPre-Training for 3D Medical Image Analysis
Abstract Vision Transformer在3D医学图像分析的自监督学习(Self-Supervised Learning,SSL)中展现了卓越的性能。掩码自编码器(Masked Auto-Encoder,MAE)用于特征预训练,可以进一步释放ViT在各…...

【STM32 学习笔记】I2C通信协议
注:通信协议的设计背景 3:00~10:13 I2C 通讯协议(Inter-Integrated Circuit)是由Phiilps公司开发的,由于它引脚少,硬件实现简单,可扩展性强, 不需要USART、CAN等通讯协议的外部收发设备,现在被广…...

【java】jdk8及以后的时间类总结
目录 1. LocalDate 2. LocalTime 4. ZonedDateTime 5. Duration 6. Period 7. DateTimeFormatter 1. LocalDate 说明:表示不带时区的日期(年、月、日),不可变且线程安全。 import java.time.LocalDate;public class Local…...

深入理解 Istio 的工作原理 v1.26.0
解读最新版本的 Istio 源码确实是一项庞大的工程,但我可以为你梳理出一个清晰的脉络,并指出关键模块和代码路径,帮助你深入理解 Istio 的工作原理。 我们主要关注 Istio 的核心组件 Istiod 和数据平面的 Envoy Proxy。 前提: Go…...

深入理解卷积神经网络的输入层:数据的起点与预处理核心
内容摘要 本文围绕卷积神经网络输入层展开,详细介绍其在网络中的重要作用,包括接收不同领域数据的形式及传递数据的过程。深入解读数据预处理的关键操作,如去均值、归一化和PCA/白化。助力读者透彻理解输入层,为构建高效卷积神经…...
redis bitmap数据类型调研
一、bitmap是什么? redis原文: Bitmaps are not an actual data type, but a set of bit-oriented operations defined on the String type . This means that bitmaps can be used with string commands, and most importantly with SET and GET. 翻…...

如何用数学思想填报高考志愿
人一辈子有很多四年,但是很少有哪个四年对你一生的影响能超过大学这四年。 从18岁到22岁的这几年,是一个人真正成年的过程,很多人会在这段时间里认识一生的朋友,谈第一次真正的恋爱,第一次离开父母,自己生…...
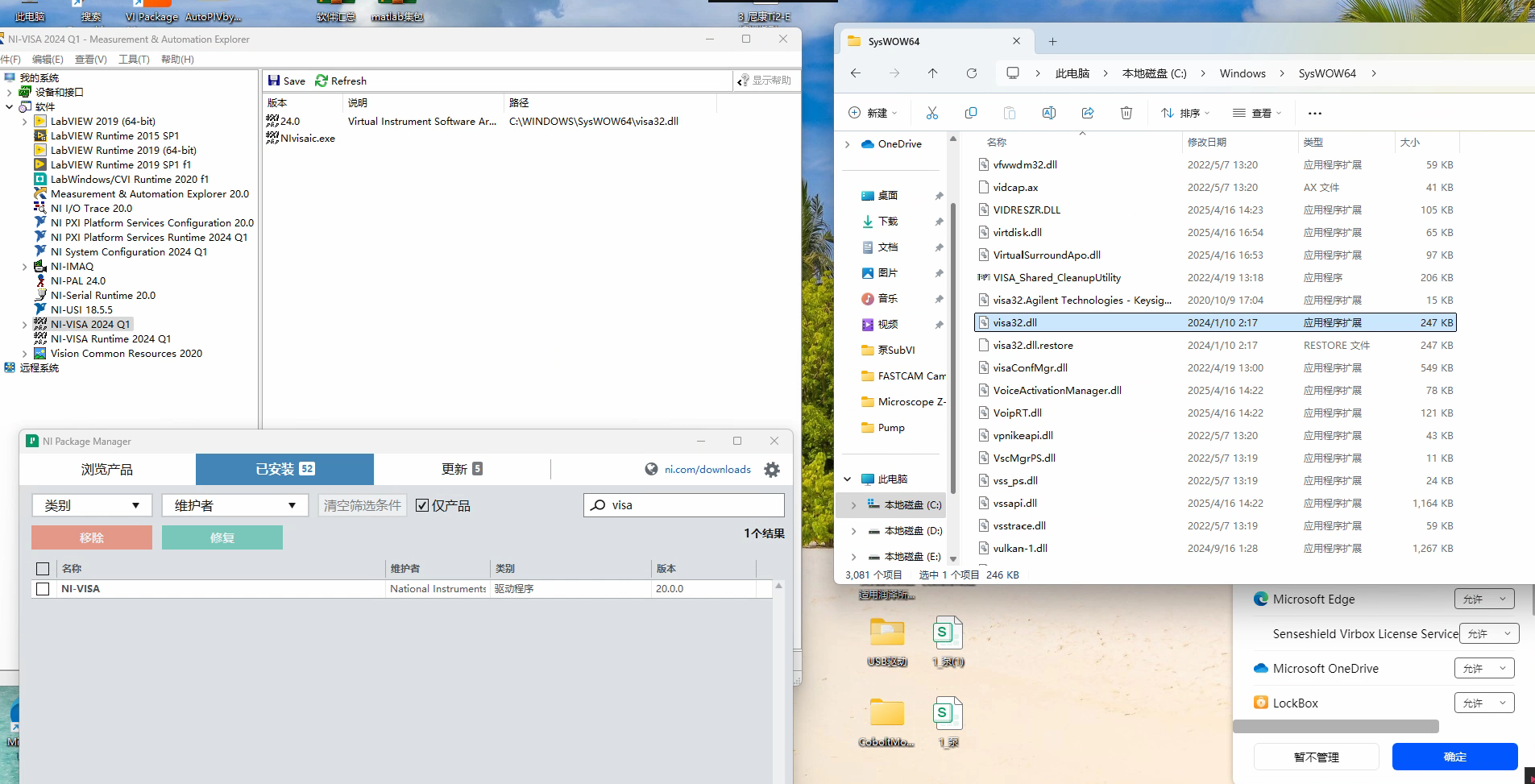
LabVIEW 2019 与 NI VISA 20.0 安装及报错处理
在使用 Windows 11 操作系统的电脑上,同时安装了 LabVIEW 2019 32 位和 64 位版本的软件。此前安装的 NI VISA 2024 Q1 版,该版本与 LabVIEW 2019 32 位和 64 位不兼容,之后重新安装了 NI VISA 20.0。从说明书来看,NI VISA 20.0 …...

探索 JWT(JSON Web Token):原理、结构与实践应用对比
目录 前言1. 什么是 JWT?2. JWT 的组成结构详解2.1 Header(头部)2.2 Payload(负载)2.3 Signature(签名) 3. JWT 的实际作用3.1 身份认证3.2 信息传递与授权 4. JWT 与 Cookie、API Key 的比较4.…...

互联网大厂Java求职面试:云原生与AI融合下的系统设计挑战-1
互联网大厂Java求职面试:云原生与AI融合下的系统设计挑战-1 在当今云计算和人工智能迅猛发展的背景下,互联网大厂对Java工程师的要求已从传统的单体架构和业务逻辑处理,转向了更复杂的云原生架构设计、AI模型集成以及高并发系统的性能优化能…...

【Redis进阶】持久化
一、MySQL事务特性及Redis持久化需求 (一)MySQL事务特性 MySQL的事务具有四大核心特性,这些特性对于保证数据库操作的准确性和可靠性至关重要。 原子性:事务中的所有操作要么全部成功,要么全部失败…...

[docker基础一]docker简介
目录 一 消除恐惧 1) 什么是虚拟化,容器化 2)案例 3)为什么需要虚拟化,容器化 二 虚拟化实现方式 1)应用程序执行环境分层 2)虚拟化常见类别 3)常见虚拟化实现 一)主机虚拟化(虚拟机)实现 二)容器虚拟化实现 一 消除恐…...

Texify - 数学公式OCR转换工具
文章目录 一、项目概览相关资源核心特性 二、安装指南三、使用示例1、命令行转换2、Python API调用3、交互式应用 四、性能基准运行你自己的基准测试 五、局限性 一、项目概览 Texify 是一个OCR模型,可将包含数学公式的图片或PDF转换为Markdown和LaTeX格式…...

RISC-V CLINT、PLIC及芯来ECLIC中断机制分析 —— RISC-V中断机制(一)
在长期的嵌入式开发实践中,对中断机制的理解始终停留在表面层次,特别当开发者长期局限于纯软件抽象层面时,对中断机制的理解极易陷入"知其然而不知其所以然"的困境,这种认知的局限更为明显;随着工作需要不断…...

时钟晶振锁相环pll方向技术要点和大厂题目解析
本专栏预计更新60期左右。当前第9期。 本专栏不仅适用于硬件的笔试面试,同样也适用于梳理硬件核心的知识点。 通过本文能得到什么? 首先,根据实战经验总结时钟晶振,锁相环的主要知识点,技术要点,面试考点; 然后,列出时钟晶振,锁相环的笔试面试的主要题型真题和模拟题,…...

图像处理篇--- HTTP|RTSP|MJPEG视频流格式
文章目录 前言一、MJPEG (Motion JPEG)基本概念技术特点编码方式传输协议数据格式 优势实现简单低延迟兼容性好容错性强 劣势带宽效率低不支持音频缺乏标准控制 典型应用 二、RTSP (Real Time Streaming Protocol)基本概念技术特点协议栈工作流程传输模式 优势专业流媒体支持高…...

【Harbor v2.13.0 详细安装步骤 安装证书启用 HTTPS】
Harbor v2.13.0 详细安装步骤(启用 HTTPS) 1. 环境准备 系统要求:至少 4GB 内存,100GB 磁盘空间。 已安装组件: Docker(版本 ≥ 20.10)Docker Compose(版本 ≥ v2.0) 域…...

C++中的static_cast:类型转换的安全卫士
C中的static_cast:类型转换的安全卫士 在C编程中,类型转换是不可避免的操作,而static_cast作为C四大强制类型转换运算符之一,是最常用且相对安全的一种转换方式。今天我们就来深入探讨一下这个重要的类型转换工具。 一、static_…...
