线性表-顺序表(Sequential List)
1 线性表
1.1 顺序表(Sequential List)
顺序表并不难理解,主要是知道顺序表是在内存中连续存储的一段数据,知道这个后,相应的算法也就非常简单了。
线性表的顺序表示指的是用一组地址连续的存储单元依次存储线性表的数据元素, 这种表示也称作线性表的顺序存储结构或顺序映像。通常, 称这种存储结构的线性表为顺序表(Sequential List)。其特点是,逻辑上相邻的数据元素, 其物理次序也是相邻的。
假设线性表的每个元素需占用 l 个存储单元,第 i + 1 个数据元素的存储位置和第 i 个元素存储的位置关系如下:
L O C ( a i + 1 ) = L O C ( a i ) + l LOC(a_{i+1}) = LOC(a_{i})+l LOC(ai+1)=LOC(ai)+l
第 i 个数据元素 a_i 的存储位置为:
L O C ( a i ) = L O C ( a 1 ) + ( i − 1 ) ∗ l LOC(a_{i}) = LOC(a_{1})+(i-1)*l LOC(ai)=LOC(a1)+(i−1)∗l
参考示意图:

线性表的基本操作在王卓老师教程和书籍的基础上进行了增加了,如下总计有11个。
InitList(&L) // 初始化操作,建立一个空的线性表L
DestroyList(&L) // 销毁已存在的线性表L
ClearList(&L) // 将线性表清空
ListInsert(&L, i, &e) // 在线性表L中第i个位置插入新元素e
ListDelete(&L, i, &e) // 删除线性表L中第i个位置元素,用e返回
ListEmpty(&L) // 若线性表为空,返回1,否则0
ListLength(&L) // 返回线性表L的元素个数
GetElem(&L, i, &e) // 将线性表L中的第i个位置元素返回给e
LocateElem(&L, &e) // L中查找与给定值e相等的元素,若成功返回该元素在表中的序号,否则返回0
PriorElem(&L, &cur_e, &pre_e) // 返回线性表cur_e的前驱元素,如果cur_e是第一个元素,则pre_e无定义
NextElem(&L, &cur_e, &next_e) // 返回线性表cur_e的后继元素,如果cur_e是最后一个元素,则next_e无定义
在实现每个方法之前需要先定义顺序表的存储结构:
// 声明 ElemType 的结构,这里为了简单方便,存储一个整数
typedef struct
{int x;
} ElemType;// 声明一个顺序表
typedef struct
{ElemType *elem;int length;
} SqList;
为了方便后续编写,声明一些常量:
// 声明一些常量
#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define TRUE 1
#define FALSE 0// Status 是函数返回值类型, 其值是函数结果状态代码。
typedef int Status;
// Boolean 定义布尔型,值就是 TRUE 和 FALSE。
typedef int Boolean;// 顺序表的元素最大为100个
#define MAXSIZE 100
这里我使用了C语言进行编写,后续代码实现我均采用C语言。
1.1.1 初始化
顺序表的初始化操作就是构造一个空的顺序表。
【算法步骤】
- 为顺序表
L动态分配一个预定义大小的数组空间,使elem指向这段空间的基地址。 - 将表的当前长度设为0。
【代码实现】
// 初始化顺序表
Status InitList(SqList *L)
{L->elem = (ElemType *)malloc(MAXSIZE * sizeof(ElemType)); // 分配初始空间if (L->elem == NULL){return OVERFLOW;}L->length = 0;return OK;
}
【算法分析】
非常容易看出,顺序表初始化算法的时间复杂度为 O(1) 。
1.1.2 销毁
销毁就是删除一个顺序表占用的内存空间。
【算法步骤】
- 检测顺序表
L的元素是否占用了内存空间,如果有则释放内存空间。 - 将表的当前长度设为0。
【代码实现】
// 销毁顺序表
Status DestroyList(SqList *L)
{if (L->elem != NULL) // 检查元素是否存在,存储在需要{free(L->elem); // 释放内存L->elem = NULL; // 防止悬空指针}L->length = 0; // 重置长度return OK;
}
【算法分析】
显然,顺序表销毁算法的时间复杂度为 O(1) 。
1.1.3 清空
清空和销毁不同,销毁需要回收一个顺序表元素占用的内存空间,清空只需要将顺序表长度置为0即可。
【算法步骤】
- 将表的当前长度设为0。
【代码实现】
// 清空顺序表
Status ClearList(SqList *L)
{L->length = 0; // 重置长度
}
【算法分析】
顺序表清空算法的时间复杂度为 O(1) 。
1.1.4 插入
在顺序表的第 i 个位置插入元素。
【算法步骤】
- 判断插入位置
i是否合法(i值的合法范围是1 ≤ i ≤ n+1),若不合法则返回ERROR。 - 判断顺序表的存储空间是否已满,若满则返回
ERROR。 - 将第
n个至第i个位置的元素依次向后移动一个位置,空出第i个位置(i = n + 1时无需移动 )。 - 将要插入的新元素
e放入第i个位置。 - 表长加 1。
【代码实现】
// 在顺序表 L 中第 i 个位置之前插入新的元素 e, i 值的合法范围是 1 ≤ i ≤ L.length + 1
Status ListInsert(SqList *L, int i, ElemType e)
{if (i < 1 && i > L->length) // i 值不合法return ERROR;if (L->length == MAXSIZE) // 存储空间已满return ERROR;for (int j = L->length - 1; j >= i - 1; j--) // 插入位置及之后的元素后移{L->elem[j + 1] = L->elem[j];}L->elem[i - 1] = e; // 将新元素放入第 i 个位置L->length++; // 表长加 1return OK;
}
【算法分析】
当在顺序表中某个位置上插入一个数据元素时,其时间主要耗费在移动元素上,而移动元素的个数取决于插入元素的位置。
假设 p i p_i pi 是在第i个元素之前插入一个元素的概率, E i n s E_{ins} Eins 为在长度为 n 的线性表中插入一个元素时所需移动元素次数的期望值(平均次数),则有:
E i n s = ∑ i = 1 n + 1 p i ( n − i + 1 ) E_{ins} = \sum_{i=1}^{n+1}p_i(n-i+1) Eins=i=1∑n+1pi(n−i+1)
公式解析:
i=1:表示插入在第 1 个位置,第 1 ~ n 个元素都需要向后移动1格,总移动次数为n = n - (i -1);i=2:表示插入在第 2 个位置,第 2 ~ n 个元素都需要向后移动1格,总移动次数为n - 1 = n - (i -1);i=3:表示插入在第 3 个位置,第 3 ~ n 个元素都需要向后移动1格,总移动次数为n - 2 = n - (i -1);- …
i=n:表示插入在第 n 个位置,第 n 个元素都需要向后移动1格,总移动次数为1 = n - (i -1);i=n+1:表示插入在最后一个位置,元素无需移动,总移动次数为0 = n - (i -1);
假定在线性表的任何位置上插入元素都是等概率的,即:
P i = 1 n + 1 P_i=\frac{1}{n+1} Pi=n+11
则前面计算平均次数的公式可以转换为:
E i n s = 1 n + 1 ∑ i = 1 n + 1 ( n − i + 1 ) = 1 n + 1 ∗ n ( n + 1 ) 2 = n 2 E_{ins} = \frac{1}{n+1}\sum_{i=1}^{n+1}(n-i+1) = \frac{1}{n+1} * \frac{n(n+1)}{2} = \frac{n}{2} Eins=n+11i=1∑n+1(n−i+1)=n+11∗2n(n+1)=2n
过程解析:求和公式实际上就是 n + (n-1) + ... + 0 ,等差数列求和。
顺序表插入算法的平均时间复杂度为 O(n) 。
1.1.5 删除
删除顺序表中第 i 个位置的元素。
【算法步骤】
- 判断插入位置
i是否合法(i值的合法范围是1 ≤ i ≤ n+1),若不合法则返回ERROR。 - 将第
i + 1个至第n个的元素依次向前移动一个位置(i=n时无需移动,即删除最后一个 )。 - 表长减 1。
【代码实现】
// 在顺序表 L 中删除第 i 个元素, i 值的合法范围是 1 ≤ i ≤ L.length + 1
Status ListDelete(SqList *L, int i)
{if (i < 1 && i > L->length) // i 值不合法return ERROR;for (int j = i; j <= L->length - 1; j++) // 被删除元素之后的元素前移{L->elem[j - 1] = L->elem[j];}--L->length; // 表长减 1return OK;
}
【算法分析】
当在顺序表中某个位置上删除一个数据元素时,其时间主要耗费在移动元素上,而移动元素的个数取决于删除元素的位置。
假设 p i p_i pi 是删除第 i 个元素的概率, E d e l E_{del} Edel 为在长度为 n 的线性表中删除一个元素时所需移动元素次数的期望值(平均次数 ),则有
E d e l = ∑ i = 1 n p i ( n − i ) E_{del} = \sum_{i=1}^{n}p_i(n-i) Edel=i=1∑npi(n−i)
假定在线性表的任何位置上删除元素都是等概率的,即:
P i = 1 n P_i=\frac{1}{n} Pi=n1
则前面计算平均次数的公式可以转换为:
E d e l = 1 n ∑ i = 1 n ( n − i ) = 1 n ∗ n ( n − 1 ) 2 = n − 1 2 E_{del} = \frac{1}{n}\sum_{i=1}^{n}(n-i) = \frac{1}{n} * \frac{n(n-1)}{2} = \frac{n-1}{2} Edel=n1i=1∑n(n−i)=n1∗2n(n−1)=2n−1
顺序表删除算法的平均时间复杂度为 O(n) 。
1.1.6 判断是否为空
【算法步骤】
- 检测顺序表的长度是否为0,为0则返回1。
【代码实现】
// 判断顺序表是否为空
Boolean IsEmpty(SqList *L)
{if (L->length == 0) return TRUE;return FALSE;
}
【算法分析】
时间复杂度为 O(1) 。
1.1.7 获取线性表的元素个数
【算法步骤】
- 线性表中的 length 通过线性表结构中的 length 属性既可获得。
【代码实现】
// 返回顺序表的长度
int ListLength(SqList *L)
{return L->length;
}
【算法分析】
时间复杂度为 O(1) 。
1.1.8 取值
根据位置 i 获取该位置的元素。
【算法步骤】
- 判断指定的位置序号
i值是否合理 (1 <= i <= L.length),若不合理,则返回ERROR。 - 若
i值合理,则将第i个数据元素L.elem[i-1]赋给参数e, 通过e返回第i个数据元素的传值。
【代码实现】
// 获取一个元素,L使用值传递的方式。
// 备注:如果 L 是按值传递,会拷贝整个 SqList 结构体,这在结构体较大时会浪费内存和时间。
Status GetElem(SqList *L, int i, ElemType *e)
{if (i < 1 || i > L->length)return ERROR;*e = L->elem[i - 1];return OK;
}
【算法分析】
直接通过 i-1 进行获取,时间复杂度为 O(1) 。
1.1.9 查找
【算法步骤】
- 从第一个元素起,依次和
e相比较,若找到与e相等的元素L.elem[i],则查找成功,返回该元素的序号i+1。 - 若查遍整个顺序表都没有找到,则查找失败, 返回0。
【代码实现】
// 在顺序表中查找元素e的位置
int LocateELem(SqList *L, ElemType *e)
{int i = 0;for (i = 0; i < L->length; i++){if (L->elem[i].x == e->x){return i + 1;}}return 0;
}
【算法分析】
A S L = ∑ i = 1 n p i C i ASL = \sum_{i=1}^np_iC_i ASL=i=1∑npiCi
- ASL(Average Search Length):平均查找长度。
- p i p_i pi :表示查找第
i个元素的概率。 - C i C_i Ci :表示为找到表中其关键字与给定值相等的第
i个记录时,和给定值已进行过比较的关键字个数。
假设每个元素的查找概率相同,即 p i = 1 / n p_i=1/n pi=1/n ;另外 C i C_i Ci 取决于所查元素在表中的位置,在顺序表中 C i = i C_i=i Ci=i 。则上面公式可以化简为:
A S L = 1 n ∑ i = 1 n i = 1 n ∗ n ( n + 1 ) 2 = n + 1 2 ASL = \frac{1}{n}\sum_{i=1}^ni = \frac{1}{n}*\frac{n(n+1)}{2} = \frac{n+1}{2} ASL=n1i=1∑ni=n1∗2n(n+1)=2n+1
因此顺序表按值查找算法的平均时间复杂度为 O(n)。
1.1.10 查找前驱
【算法步骤】
- 调用 查找 算法,得到所查找的元素所在位置
i; - 判断位置
i是否合法(i值的合法范围是2 ≤ i ≤ L.length,第一个元素没有前驱元素),若不合法则返回0。 - 如果
i合法,则L.elem[i-2]即为要查找的上一个元素,保存在返回的pre_e中。 - 返回前驱元素的位置
i-1。
【代码实现】
// 查找前驱元素,cur_e表示要查找的元素,返回的结果存放在pre_e
int PriorElem(SqList *L, ElemType *cur_e, ElemType *pre_e)
{int i = LocateELem(L, cur_e);if (i < 2 || i > L->length) // i 值不合法,第1个元素没有前驱return 0;*pre_e = L->elem[i - 2]; // 下标从0开始计算return i - 1;
}
【算法分析】
该算法依赖 查找 算法,查找算法的平均时间复杂度为 O(n),查找后的代码运行时间复杂度是常量阶 O(1),所以整体的时间复杂度是 O(n)。
1.1.11 查找后继
【算法步骤】
- 调用 查找 算法,得到所查找的元素所在位置
i; - 判断位置
i是否合法(i值的合法范围是1 ≤ i ≤ L.length-1,最后一个没有后继元素 ),若不合法则返回0。 - 如果
i合法,则L.elem[i]即为要查找的下一个元素,保存在返回的next_e中。 - 返回后继元素的位置
i + 1。
【代码实现】
// 查找后继元素,cur_e表示要查找的元素,返回的结果存放在next_e
int NextElem(SqList *L, ElemType *cur_e, ElemType *next_e)
{int i = LocateELem(L, cur_e);if (i < 1 || i > L->length - 1) // i 值不合法,最后一个元素没有后继return 0;*next_e = L->elem[i];return i + 1;
}
【算法分析】
该算法依赖 查找 算法,查找算法的平均时间复杂度为 O(n),查找后的代码运行时间复杂度是常量阶 O(1),所以整体的时间复杂度是 O(n)。
相关文章:

线性表-顺序表(Sequential List)
1 线性表 1.1 顺序表(Sequential List) 顺序表并不难理解,主要是知道顺序表是在内存中连续存储的一段数据,知道这个后,相应的算法也就非常简单了。 线性表的顺序表示指的是用一组地址连续的存储单元依次存储线性表的…...
)
框架篇八股(自用)
框架篇 Spring框架中的bean不是线程安全的 Scope() singleton单例 prototype多例 一个类中有可修改的成员变量需要考虑线程安全 bean没有可变状态(service类,DAO类) 某种程度单例bean是线程安全的 AOP面向切面编程…...
)
软考高级《系统架构设计师》知识点(十七)
知识产权和标准化 知识产权基础知识 知识产权是指公民、法人、非法人单位、对自己的创造性智力成果和其他科技成果依法享有的民事权。是智力成果的创造人依法享有的权利和在生产经营活动中标记所有人依法所享有的权利的总称。 知识产权基础知识包含著作权、专利权、商标权、商业…...

在 Envoy 的配置文件中出现的 “@type“ 字段
在 Envoy 的配置文件中出现的 "type" 字段是 Protocol Buffers(Protobuf)的 JSON/YAML 编码规范的一部分,属于 Typed Struct 的表示方式。它的作用是明确指定当前配置对象的 Protobuf 类型,以便 Envoy 正确解析配置。以…...

思维链实现 方式解析
思维链的实现方式 思维链的实现方式除了提示词先后顺序外,还有以下几种: 增加详细的中间步骤提示:通过提供问题解决过程中的详细中间步骤提示,引导模型逐步推导和思考。例如,在解决数学证明题时,提示词可以具体到每一步需要运用的定理、公式以及推理的方向,帮助模型构建…...

计算机网络:什么是Mesh组网以及都有哪些设备支持Mesh组网?
Mesh组网技术详解与实现工具推荐 Mesh组网是一种通过多个节点路由器协同工作,形成覆盖全屋的无线网络的技术。它通过动态路径调整、无缝漫游和自愈能力,解决传统单一路由器覆盖不足的问题,尤其适合大户型、多层住宅或复杂户型环境。以下是Mesh组网的核心原理、实现方式及推…...

【阿里云免费领取域名以及ssl证书,通过Nginx反向代理web服务】
文章目录 前言一、申请域名1.1 访问阿里云官网1.2 输入自定义域名1.3 创建个人模板1.4 支付1元可以使用域名1年1.5 按照提示实名认证1.6 实名认证成功 二、域名解析2.1 选择域名解析2.2 解析设置2.3 快速添加解析2.4 选择对应类型2.5 解析成功 三、申请免费ssl证书3.1 访问阿里…...
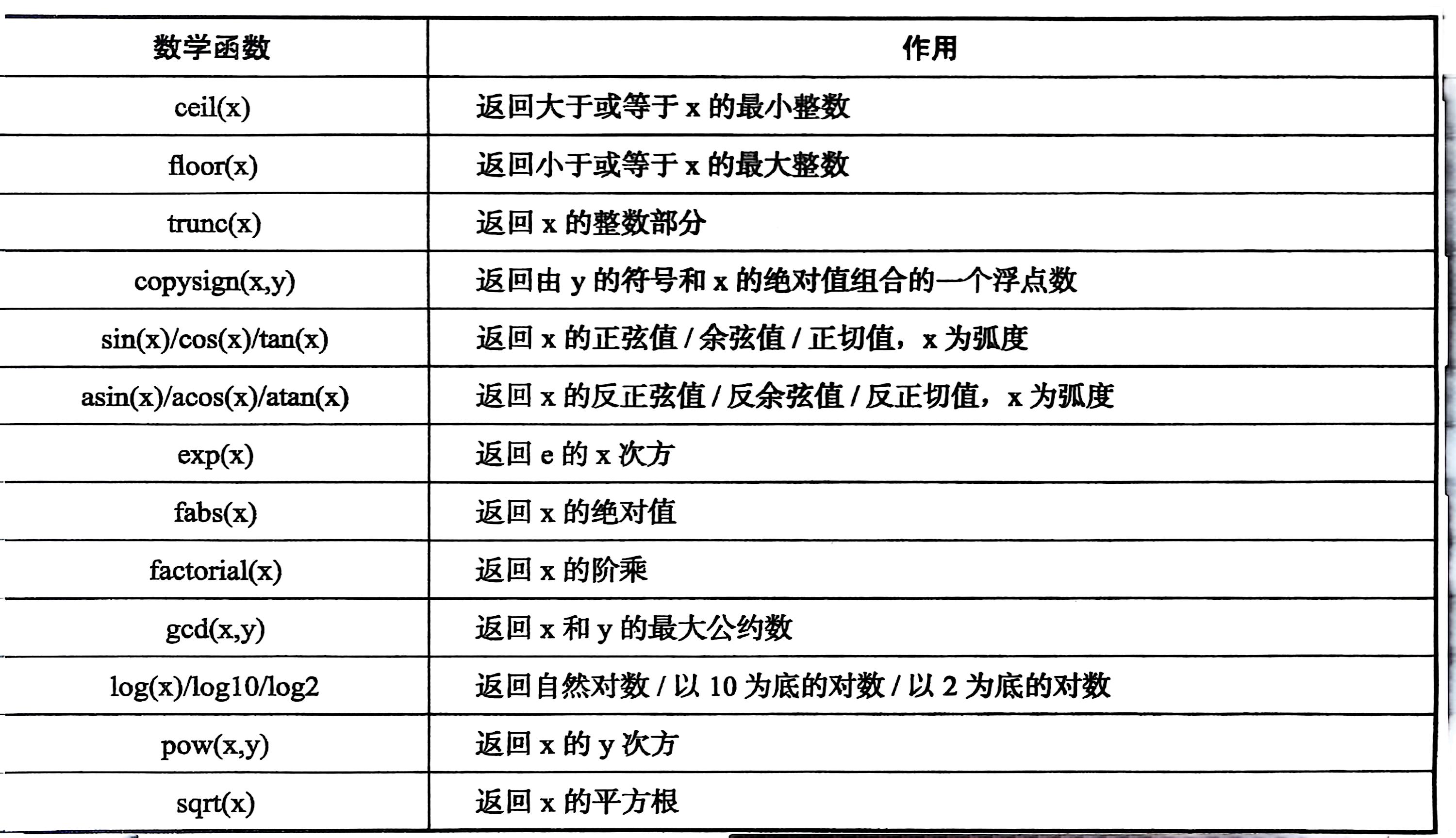
数据分析2
五、文件 CSV Comma-Separated Value,逗号分割值。CSV文件以纯文本形式存储表格数据(数字和文本)。 CSV记录间以某种换行符分隔,每条记录由字段组成,字段间以其他字符或字符串分割,最常用逗号或制表符。…...

实战项目5(08)
目录 任务场景一 【r1配置】 【r2配置】 【r3配置】 任务场景二 【r1配置】 【r2配置】 任务场景一 按照下图完成网络拓扑搭建和配置 任务要求: 通过在路由器R1、R2和R3上配置静态路由,实现网络中各终端PC能够正常…...

CSS结构性伪类、UI伪类与动态伪类全解析:从文档结构到交互状态的精准选择
一、结构性伪类选择器:文档树中的位置导航器 结构性伪类选择器是CSS中基于元素在HTML文档树中的层级关系、位置索引或结构特征进行匹配的一类选择器。它们无需依赖具体的类名或ID,仅通过文档结构即可精准定位元素,是实现响应式布局和复杂文档…...

.NET MAUI 基础知识
文章目录 什么是 .NET MAUI?MAUI的核心特点与Xamarin.Forms的区别 开发环境搭建安装Visual Studio 2022安装必要组件配置Android开发环境配置iOS开发环境验证安装 创建第一个MAUI应用创建新项目MAUI项目结构解析理解关键文件运行应用程序简单修改示例使用热重载 MAU…...
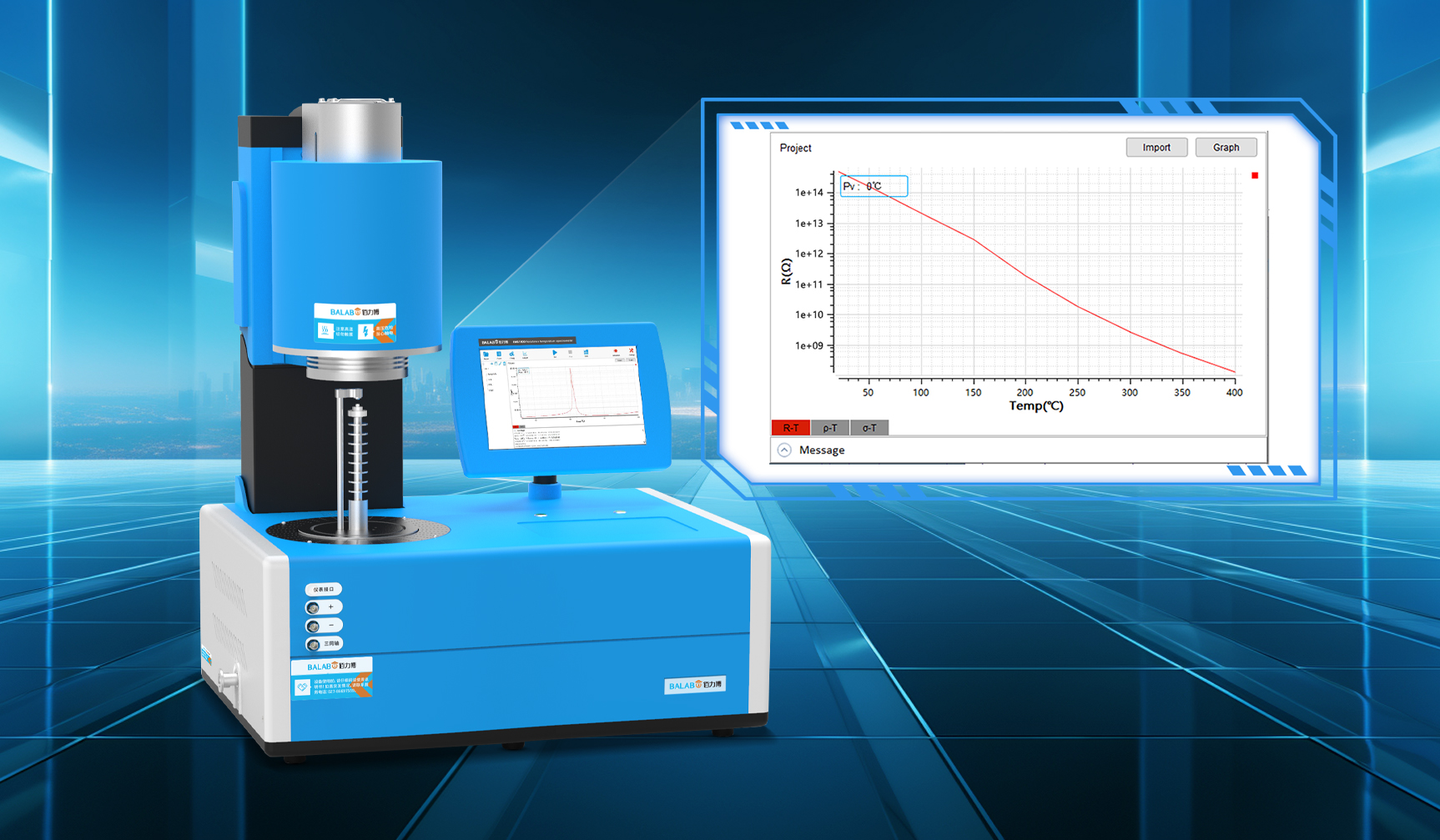
佰力博科技与您探讨表面电阻的测试方法及应用领域
表面电阻测试是一种用于测量材料表面电阻值的技术,广泛应用于评估材料的导电性能、静电防护性能以及绝缘性能。 1、表面电阻的测试测试方法: 表面电阻测试通常采用平行电极法、同心圆电极法和四探针法等方法进行。其中,平行电极法通过在试样…...

鹅厂面试数学题
题目 一个圆上随机取三个点,求这三个点构成锐角三角形的概率。 解答 根据圆周角定理,此题目等价为:一条线段长度为1的线段随机取两个点分成三段,任意一段长度均不大于1/2的概率。记前两段的长度为,则第三段的长度为…...

GO语言-导入自定义包
文章目录 1. 项目目录结构2. 创建自定义包3. 初始化模块4. 导入自定义包5. 相对路径导入 在Go语言中导入自定义包需要遵循一定的目录结构和导入规则。以下是详细指南(包含两种方式): 1. 项目目录结构 方法1:适用于Go 1.11 &#…...

java基础-package关键字、MVC、import关键字
1.package关键字: (1)为了更好管理类,提供包的概念 (2)声明类或接口所属的包,声明在源文件首行 (3)包,属于标识符,用小写字母表示 ࿰…...

[6-2] 定时器定时中断定时器外部时钟 江协科技学习笔记(41个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 V 30 31 32 33 34 35 36 37 38 39 40 41...

第五节:对象与原型链:JavaScript 的“类”与“继承”
📌 第五节:对象与原型链:JavaScript 的“类”与“继承” 目标:理解对象创建、原型继承、this 绑定,掌握类语法与原型设计模式,实现模块化组件开发。 一、对象基础:数据的“容器” 1. 对象字面…...
)
本地的ip实现https访问-OpenSSL安装+ssl正式的生成(Windows 系统)
1.下载OpenSSL软件 网站地址:Win32/Win64 OpenSSL Installer for Windows - Shining Light Productions 安装: 一直点击下一步就可以了 2.设置环境变量 在开始菜单右键「此电脑」→「属性」→「高级系统设置」→「环境变量」 在Path 中添加一个: xxxx\OpenSSL-…...

Spring Boot + MyBatis-Plus 高并发读写分离实战
引言 在高并发场景下,单一数据库实例往往成为性能瓶颈。数据库读写分离通过将读操作和写操作分配到不同的数据库实例,有效缓解主库压力,提升系统吞吐量。MyBatis-Plus 作为一款强大的持久层框架,结合 Spring Boot 能够轻松实现读…...
)
HarmonyOS 【诗韵悠然】AI古诗词赏析APP开发实战从零到一系列(二、项目准备与后台服务搭建)
在开发一款面向HarmonyOS平台的应用程序——【诗韵悠然】AI古诗词赏析APP时,选择了流行Go语言作为后端开发语言,并使用了go-zero微服务框架来搭建服务接口。本文将详细介绍项目准备和后台服务搭建的过程,帮助大家更好地理解和掌握go-zero框架…...

【PmHub后端篇】PmHub中基于自定义注解和AOP的服务接口鉴权与内部认证实现
1 引言 在现代软件开发中,尤其是在微服务架构下,服务接口的鉴权和内部认证是保障系统安全的重要环节。本文将详细介绍PmHub中如何利用自定义注解和AOP(面向切面编程)实现服务接口的鉴权和内部认证,所涉及的技术知识点…...

多模态AI新纪元:Vertex AI Gemini与Spring AI深度集成实践
企业级AI集成进阶:Spring AI与Vertex AI Gemini的配置与调优实战 一、前沿技术:多模态模型的企业级配置范式 在生成式AI技术快速迭代的当下,企业级应用对模型配置的精细化需求日益增长。Vertex AI Gemini作为Google推出的多模态大模型&…...

大语言模型RLHF训练框架全景解析:OpenRLHF、verl、LLaMA-Factory与SWIFT深度对比
引言 随着大语言模型(LLM)参数规模突破千亿级,基于人类反馈的强化学习(RLHF)成为提升模型对齐能力的关键技术。OpenRLHF、verl、LLaMA-Factory和SWIFT作为开源社区的四大标杆框架,分别通过分布式架构、混合…...

开源AI数字人分身克隆小程序源码系统深度剖析:从搭建到应用
在人工智能与小程序生态深度融合的当下,开源 AI 数字人分身克隆小程序源码成为开发者的热门工具。从搭建基础环境到实现实际应用,这一过程涉及多项技术与复杂流程。本文将带您深入剖析开源 AI 数字人分身克隆小程序源码,揭开其从搭建到应用的…...

ETL背景介绍_1:数据孤岛仓库的介绍
1 ETL介绍 1.1 数据孤岛 随着企业内客户数据大量的涌现,单个数据库已不再足够。为了储存这些数据,公司通常会建立多个业务部门组织的数据库来保存数据。比如,随着数据量的增长,公司通常可能会构建数十个独立运行的业务数据库&am…...

Linux系统:虚拟文件系统与文件缓冲区(语言级内核级)
本节重点 初步理解一切皆文件理解文件缓冲区的分类用户级文件缓冲区与内核级文件缓冲区用户级文件缓冲区的刷新机制两级缓冲区的分层协作 一、虚拟文件系统 1.1 理解“一切皆文件” 我们都知道操作系统访问不同的外部设备(显示器、磁盘、键盘、鼠标、网卡&#…...

智能体的典型应用:自动驾驶、智能客服、智能制造、游戏AI与数字人技术
本文为《React Agent:从零开始构建 AI 智能体》专栏系列文章。 专栏地址:https://blog.csdn.net/suiyingy/category_12933485.html。项目地址:https://gitee.com/fgai/react-agent(含完整代码示例与实战源)。完整介绍…...

【技巧】使用UV创建python项目的开发环境
回到目录 【技巧】使用UV创建python项目的开发环境 0. 为什么用UV 下载速度快、虚拟环境、多版本python支持、清晰的依赖关系 1. 安装基础软件 1.1. 安装python 下载地址:https://www.python.org/downloads/windows/ 1.2. 安装UV > pip install uv -i ht…...

什么是时序数据库?
2025年5月13日,周二清晨 时序数据库(Time Series Database,TSDB)是一种专门用于高效存储、管理和分析时间序列数据的数据库系统。时间序列数据是指按时间顺序记录的数据点,通常包含时间戳和对应的数值或事件࿰…...

react父组件往孙子组件传值Context API
步骤: 创建一个 Context 在父组件中用 Provider 提供值 在孙子组件中用 useContext 消费值 // 创建 Context const MyContext React.createContext();// 父组件 const Parent () > {const value "Hello from parent";return (<MyContext.Provid…...
