LLM大模型中的基础数学工具—— 信号处理与傅里叶分析
Q51: 推导傅里叶变换  的 Parseval 定理
的 Parseval 定理
傅里叶变换的 Parseval 定理揭示了啥关系?
Parseval 定理揭示了傅里叶变换中时域与频域的能量守恒关系,即信号在时域的总能量等于其在频域的总能量。这就好比一个物体无论从哪个角度称重,重量始终不变,确保了信号在不同域表示时的能量一致性。
推导过程
Parseval 定理的数学形式为:。从右边开始推导:
这里利用了
(狄拉克函数,在
时为无穷大,否则为 0),最终左边等于右边,定理得证。
在 LLM 中的使用
在 LLM 的训练数据预处理中,若输入包含音频,可通过 Parseval 定理检测数据是否异常。例如,某段音频在时域能量正常但频域异常,可能存在噪声或损坏。在文本生成的注意力机制中,该定理可类比为信息在不同表示空间的能量守恒,确保信息完整性。
代码示例
import numpy as np
import matplotlib.pyplot as plt
# 生成一个模拟音频信号(假设为某个词的发音片段)
x = np.linspace(-1, 1, 1000)
f = np.exp(-(x ** 2) / 0.5) # 模拟音频的时域信号
# 计算傅里叶变换
f_hat = np.fft.fftshift(np.fft.fft(f))
xi = np.fft.fftshift(np.fft.fftfreq(len(x), x[1] - x[0]))
# 计算时域能量
energy_time = np.sum(np.abs(f) ** 2) * (x[1] - x[0])
# 计算频域能量
energy_freq = np.sum(np.abs(f_hat) ** 2) * (xi[1] - xi[0])
print(f"时域能量: {energy_time:.4f}")
print(f"频域能量: {energy_freq:.4f}")
代码解释:生成一个模拟音频信号 f,通过 FFT 计算其频域表示 。分别计算时域和频域能量,验证 Parseval 定理。这有助于在 LLM 处理音频输入时,确保能量一致性,提升语音识别或生成的准确性。
Q52: 证明卷积定理 
卷积定理在傅里叶变换中有啥关键作用?
卷积定理表明,时域的卷积操作对应频域的乘积操作。这在 LLM 处理序列数据时非常关键,例如文本中的词与词的关联(卷积)可以转换到频域分析,大大简化计算复杂度。
证明过程
设 (卷积的定义,即将 g 翻转后在 f 上滑动相乘积分),对其进行傅里叶变换:
令
,交换积分次序后,就得到了频域相乘的结果,证明了卷积定理。
在 LLM 中的使用
在 LLM 的卷积神经网络(CNN)层处理文本时,卷积核与输入特征的卷积可转换为频域相乘,加速计算。例如,在文本分类中,通过频域分析提取关键特征,提升分类效率。
代码示例
import numpy as np
import matplotlib.pyplot as plt
# 生成两个信号(模拟文本特征)
x = np.linspace(-5, 5, 1000)
f = np.exp(-(x ** 2) / 2)
g = np.exp(-(x ** 2) / 8)
# 计算时域卷积
conv_time = np.convolve(f, g, 'same')
# 计算傅里叶变换
f_hat = np.fft.fft(f)
g_hat = np.fft.fft(g)
conv_freq = np.fft.ifft(f_hat * g_hat)
# 对比结果
plt.plot(x, conv_time, label='时域卷积')
plt.plot(x, np.real(conv_freq), label='频域相乘逆变换')
plt.legend()
plt.show()
代码解释:生成两个模拟文本特征的信号 f 和 g,分别计算时域卷积和频域相乘逆变换的结果,验证卷积定理。这有助于 LLM 在处理文本特征时,选择更高效的计算方式。
Q53: 分析离散傅里叶变换(DFT)的频域采样性质
DFT 的频域采样在 LLM 中如何助力数据处理?
DFT 的频域采样性质指频域样本对应时域信号的周期延拓。在 LLM 处理变长文本或音频时,可通过频域采样压缩数据,保留关键信息,减少计算量。
分析过程
设 是长度为 N 的离散信号,DFT 为
。若频域采样
(M 为间隔),相当于
周期延拓为
。频域采样间隔 M 决定时域延拓周期,数学上可通过 DFT 的定义和周期性证明。例如,若
,
,则时域信号会被延拓成周期为 20 的信号。
在 LLM 中的使用
在 LLM 处理音频文本对时,对音频 DFT 频域采样,减少数据量,同时保留关键频率信息,提升处理效率。例如,在语音识别中,先对音频进行频域采样,再输入模型,加快处理速度。
代码示例
import numpy as np
import matplotlib.pyplot as plt
# 生成离散信号(模拟音频片段)
N = 100
n = np.arange(N)
x = np.sin(2 * np.pi * 5 * n / N) + 0.5 * np.sin(2 * np.pi * 12 * n / N)
# 计算DFT
X = np.fft.fft(x)
# 频域采样(每隔5点采样)
M = 5
X_sampled = X[::M]
# 计算逆DFT
x_recon = np.fft.ifft(X_sampled)
x_recon = np.concatenate([x_recon] * M)[:N]
plt.plot(n, x, label='原信号')
plt.plot(n, x_recon, label='频域采样逆变换信号')
plt.legend()
plt.show()
代码解释:生成含两个频率成分的离散信号 x,计算 DFT 后频域采样,逆变换观察时域效果。这模拟了 LLM 处理音频时的采样压缩过程,验证频域采样性质的实际应用。
Q54: 推导小波变换(Wavelet Transform)的多分辨率分析公式
小波变换的多分辨率分析如何助力 LLM 特征提取?
小波变换的多分辨率分析可将信号分解为不同频率分辨率的部分,在 LLM 处理图像或音频输入时,先粗后细分析特征,提升模型对细节的捕捉能力。就像用不同倍数的放大镜观察物体,先看整体再看局部。
推导过程
多分辨率分析满足 ,其中
由尺度函数
张成(
是尺度函数,如常见的 Daubechies 尺度函数),而
(
中
的补空间)由小波函数
张成。信号
可分解为:
其中
(尺度系数,反映粗尺度信息),
(小波系数,反映细节信息)。通过尺度函数的双尺度方程
(
是低通滤波器系数)和小波函数与尺度函数的关系
(
是高通滤波器系数),可以递推计算不同尺度的系数,实现多分辨率分解。
在 LLM 中的使用
在 LLM 处理图像生成时,小波多分辨率分析可先处理整体图像结构(粗尺度),再细化纹理细节(细尺度)。处理音频时,分离不同频率成分,提升语音识别准确性。例如,在生成高分辨率图像时,先确定大致轮廓,再逐步添加细节;在语音识别中,先捕捉低频的语音轮廓,再分析高频的细节特征。
代码示例
import pywt
import numpy as np
import matplotlib.pyplot as plt
# 生成信号(模拟图像边缘信息或音频特征)
x = np.linspace(0, 1, 1024)
signal = np.sin(2 * np.pi * 10 * x) + 0.5 * np.sin(2 * np.pi * 30 * x)
# 进行小波多分辨率分析(用db1小波,分解3层)
coeffs = pywt.wavedec(signal, 'db1', level=3)
# 重构信号
rec_signal = pywt.waverec(coeffs, 'db1')
plt.plot(x, signal, label='原信号')
plt.plot(x, rec_signal, label='重构信号(多分辨率)')
plt.legend()
plt.show()
代码解释:使用 PyWavelets 库对信号进行 3 层 db1 小波分解与重构。原信号包含 10Hz 和 30Hz 成分,重构信号会综合各尺度信息。运行代码会发现,重构信号与原信号相似,但经过多分辨率处理后,能更清晰地展示不同尺度的特征,模拟 LLM 处理图像或音频时的特征提取与重建过程。
Q55: 验证 Nyquist - Shannon 采样定理的重构条件
Nyquist - Shannon 采样定理如何保障 LLM 输入质量?
Nyquist - Shannon 采样定理是信号采样的 “黄金法则”:如果采样频率至少是信号最高频率的两倍,那么就可以从采样点无失真地重构原信号。在 LLM 处理音频或图像输入时,遵循此定理可避免信息丢失,确保输入质量。
验证过程
设信号 最高频率为 B,采样频率
,采样信号
(
是采样间隔)。其傅里叶变换
(频谱发生周期延拓)。通过理想低通滤波器
(截止频率 B,增益 T),输出
,逆变换得:
这就是 sinc 插值公式,只要采样频率满足定理,就能无失真重构原信号。
在 LLM 中的使用
音频 CD 的采样率定为 44.1kHz,因为人耳能听到的最高频率约 20kHz,44.1kHz 满足两倍要求。在 LLM 处理音频输入时,按此定理采样确保语音识别准确。处理图像时,避免混叠现象(如摩尔纹),保证图像生成质量。例如,在训练图像生成模型时,确保采样符合定理,避免生成图像出现失真。
代码示例
import numpy as np
import matplotlib.pyplot as plt
# 原信号(5Hz正弦波)
t = np.linspace(-1, 1, 1000)
f = np.sin(2 * np.pi * 5 * t)
# 采样频率(12Hz,高于10Hz)
fs = 12
Ts = 1 / fs
n = np.arange(-10, 10)
t_sampled = n * Ts
f_sampled = np.sin(2 * np.pi * 5 * t_sampled)
# 重构信号(sinc插值)
t_recon = np.linspace(-1, 1, 1000)
f_recon = np.zeros_like(t_recon)
for n_val in n: f_recon += f_sampled[n_val + 10] * np.sin(np.pi * (t_recon - n_val * Ts) / Ts) / (np.pi * (t_recon - n_val * Ts) / Ts)
plt.figure(figsize=(10, 5))
plt.plot(t, f, label='原信号')
plt.plot(t_recon, f_recon, label='重构信号')
plt.legend()
plt.show()
代码解释:生成 5Hz 的正弦波,以 12Hz 采样(满足定理)。通过 sinc 插值重构信号,运行代码会发现,重构信号与原信号几乎完全重合,验证了定理的正确性,确保 LLM 处理音频输入时的准确性。
Q56: 分析快速傅里叶变换(FFT)的递归分治复杂度 
FFT 的高效复杂度如何助力 LLM 处理大数据?
FFT 是 DFT 的 “快速通道”,它通过分治策略,把原本 复杂度的 DFT 运算降到
。在 LLM 处理海量文本或音频数据时,这种高效性至关重要,能大幅减少计算时间。
分析过程
设 (为简化,假设 N 是 2 的幂),FFT 将 N 点 DFT 分解为两个
点 DFT,递归公式为
。展开这个递归:
每一级递归都需要处理
的操作(如蝶形运算),而总共有 log N 级递归(因为每次规模减半),所以总复杂度是
。
在 LLM 中的使用
在实时音频处理中,FFT 能快速计算音频的频谱,实现实时音效调整,如在语音交互应用中实时分析用户语音的频谱特征。在雷达信号处理或大规模文本的频谱分析中,FFT 的高效性使得实时处理成为可能,例如在文本分类中快速提取文本的频率特征。
代码示例
import numpy as np
import time
# 测试不同N下FFT的计算时间
Ns = [1024, 2048, 4096, 8192]
for N in Ns: x = np.random.randn(N) # 生成随机信号 start = time.time() np.fft.fft(x) # 计算FFT end = time.time() print(f"N = {N}, 计算时间: {end - start:.6f} 秒")
代码解释:对不同长度 N 的随机信号进行 FFT 计算,记录时间。运行代码会发现,随着 N 翻倍,时间大约增加 log N 倍,验证了 的复杂度。例如,N 从 1024 到 2048,时间不会翻倍,而是增加约
倍左右(实际因系统差异略有不同,但趋势一致),确保 LLM 处理数据的高效性。
Q57: 推导滤波器设计中的 Z 变换极点稳定性条件
Z 变换极点稳定性如何确保 LLM 滤波器可靠?
在滤波器设计中,Z 变换 的极点位置决定了滤波器是否稳定。稳定的滤波器能保证输入有界信号,输出也有界(BIBO 稳定),这对 LLM 处理音频或图像的滤波操作至关重要。
推导过程
系统稳定要求 (单位脉冲响应绝对可和)。对于因果系统(输出只取决于当前和过去输入),
的收敛域是
。稳定的条件是所有极点都在单位圆内(
)。假设
,其中
,极点是
的根。如果每个根
,则系统稳定。例如,对于
,极点
在单位圆内,系统稳定。
在 LLM 中的使用
设计低通滤波器去除音频噪声时,需检查极点是否在单位圆内,否则滤波器可能会发散,导致降噪失败。在双线性变换法设计 IIR 滤波器时,调整参数确保极点位置正确,避免系统不稳定。例如,在 LLM 处理音频输入时,设计稳定的滤波器去除背景噪声,确保语音清晰。
代码示例
import numpy as np
import matplotlib.pyplot as plt
# 定义滤波器分母系数(比如1 - 1.5z^{-1} + 0.7z^{-2})
a = [1, -1.5, 0.7]
# 计算极点
pole = np.roots(a[::-1]) # 注意系数顺序,np.roots求多项式根
print(f"极点: {pole}")
# 检查稳定性
is_stable = np.all(np.abs(pole) < 1)
print(f"滤波器是否稳定: {is_stable}")
# 绘制极点和单位圆
plt.figure(figsize=(6, 6))
plt.plot(np.real(pole), np.imag(pole), 'ro', label='极点')
theta = np.linspace(0, 2 * np.pi, 100)
plt.plot(np.cos(theta), np.sin(theta), 'b', label='单位圆')
plt.axis('equal')
plt.legend()
plt.show()
代码解释:定义滤波器的分母系数 a,计算极点并判断是否在单位圆内。运行代码会绘制出极点和单位圆,直观展示稳定性。如果极点都在单位圆内,输出 “True”,否则 “False”,确保 LLM 中滤波器设计的可靠性。
Q58: 证明维纳滤波(Wiener Filter)的最小均方误差解
维纳滤波如何提升 LLM 处理噪声数据的能力?
维纳滤波是从含噪信号中恢复原信号的 “魔法镜”,它通过最小化均方误差(MSE)来找到最佳的滤波方式,在 LLM 处理噪声数据(如含噪音频或图像)时,能有效提升输入质量。
证明过程
设含噪信号 (
是原信号,
是噪声),维纳滤波器输出
。均方误差
。在频域中:
对
求导并令导数为 0(求最小值):
其中
是原信号功率谱,
是噪声功率谱。这表明,维纳滤波器的频域响应由信号和噪声的功率谱决定。
在 LLM 中的使用
在语音通话中,背景噪声会干扰语音,维纳滤波可以根据语音和噪声的功率谱,自动调整滤波系数,去除噪声保留清晰语音,提升 LLM 的语音识别准确率。在图像去噪中,区分图像信号和噪声的功率谱,去除噪声点,保留图像细节,提高 LLM 处理图像的质量。
代码示例
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import wiener
# 生成原信号(模拟语音)
t = np.linspace(0, 1, 1000)
x = np.sin(2 * np.pi * 5 * t)
# 加噪声(高斯白噪声)
n = 0.5 * np.random.randn(len(t))
y = x + n
# 应用维纳滤波(窗口大小31,可调整)
x_hat = wiener(y, mysize=31)
plt.figure(figsize=(10, 5))
plt.plot(t, y, label='含噪信号')
plt.plot(t, x_hat, label='维纳滤波输出')
plt.plot(t, x, label='原信号')
plt.legend()
plt.show()
代码解释:生成正弦波 x,加入噪声得到 y。使用 scipy 的 wiener 函数进行滤波,调整窗口大小可以控制去噪效果。运行代码会发现,滤波后的信号 接近原信号 x,噪声被有效去除,展示了维纳滤波在 LLM 处理噪声数据时的实际应用效果。
相关文章:
LLM大模型中的基础数学工具—— 信号处理与傅里叶分析
Q51: 推导傅里叶变换 的 Parseval 定理 傅里叶变换的 Parseval 定理揭示了啥关系? Parseval 定理揭示了傅里叶变换中时域与频域的能量守恒关系,即信号在时域的总能量等于其在频域的总能量。这就好比一个物体无论从哪个角度称重,重量始终不…...

calico.yaml+国内源
pod网段为:10.244.0.0/16 #kubeadm init 时设置的pod网段,每个环境不同,参考自身环境。 calico.yaml文件里的镜像均为: swr.cn-north-4.myhuaweicloud.com/ddn-k8s/docker.io/calico/cni:v3.26.1 swr.cn-north-4.myhuaweiclou…...

橡胶制品行业质检管理的痛点 质检LIMS如何重构橡胶制品质检价值链
橡胶制品广泛应用于汽车、医疗、航空等领域,其性能稳定性直接关联终端产品的安全性。从轮胎耐磨性测试到密封件耐腐蚀性验证,每一项检测数据都是企业参与市场竞争的核心筹码。然而,传统实验室管理模式普遍面临设备调度混乱、检测流程追溯断层…...

5.2 参数管理
目标 访问参数,用于调试、诊断和可视化;参数初始化;在不同模型组件间共享参数。 模型:单隐藏层的MLP import torch from torch import nnnet nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1)) X torch.rand(size…...

gvm安装go报错ERROR: Failed to use installed version
这里写自定义目录标题 使用gvm安装版本报错解决方案可以尝试在版本后面添加--binary,例如还不行记得在多切换几个准确的版本 使用gvm安装版本报错 gvm install go1.22 Installing go1.22.0 as go1.22… Compiling… /Users/uncledd2/.gvm/scripts/install: line 9…...

CAElinux系统详解
CAElinux 系统详解:从系统层面到专业应用 一、CAElinux 的定位与核心目标 CAElinux 是一款专门为 计算机辅助工程(CAE) 设计的定制化 Linux 发行版,目标用户为从事工程仿真、数值模拟、高性能计算(HPC)的…...

计算机系统----软考中级软件设计师(自用学习笔记)
目录 1、计算机的基本硬件系统 2、CPU的功能 3、运算器的组成 4、控制器 5、计算机的基本单位 6、进制转换问题 7、原码、反码、补码、移码 8、浮点数 9、寻址方式 10、奇偶校验码 11、海明码 12、循环冗余校验码 13、RISC和CISC 14、指令的处理方式 15、存储器…...

django的权限角色管理(RBAC)
在 Django 中,User、Group 和 Permission 是权限系统的核心组件。下面通过代码示例演示它们的 CRUD(创建、读取、更新、删除) 操作: 一、User 模型 CRUD from django.contrib.auth.models import User# 创建用户 user User.obje…...

新建一个reactnative 0.72.0的项目
npx react-native0.72.0 init ProjectName --version 0.72.0 下面是初始化,并且添加了对应路由的库依赖,Android项目能run起来的版本号 { "name": "ProjectName", "version": "0.0.1", "private&quo…...

线性表-顺序表(Sequential List)
1 线性表 1.1 顺序表(Sequential List) 顺序表并不难理解,主要是知道顺序表是在内存中连续存储的一段数据,知道这个后,相应的算法也就非常简单了。 线性表的顺序表示指的是用一组地址连续的存储单元依次存储线性表的…...
)
框架篇八股(自用)
框架篇 Spring框架中的bean不是线程安全的 Scope() singleton单例 prototype多例 一个类中有可修改的成员变量需要考虑线程安全 bean没有可变状态(service类,DAO类) 某种程度单例bean是线程安全的 AOP面向切面编程…...
)
软考高级《系统架构设计师》知识点(十七)
知识产权和标准化 知识产权基础知识 知识产权是指公民、法人、非法人单位、对自己的创造性智力成果和其他科技成果依法享有的民事权。是智力成果的创造人依法享有的权利和在生产经营活动中标记所有人依法所享有的权利的总称。 知识产权基础知识包含著作权、专利权、商标权、商业…...

在 Envoy 的配置文件中出现的 “@type“ 字段
在 Envoy 的配置文件中出现的 "type" 字段是 Protocol Buffers(Protobuf)的 JSON/YAML 编码规范的一部分,属于 Typed Struct 的表示方式。它的作用是明确指定当前配置对象的 Protobuf 类型,以便 Envoy 正确解析配置。以…...

思维链实现 方式解析
思维链的实现方式 思维链的实现方式除了提示词先后顺序外,还有以下几种: 增加详细的中间步骤提示:通过提供问题解决过程中的详细中间步骤提示,引导模型逐步推导和思考。例如,在解决数学证明题时,提示词可以具体到每一步需要运用的定理、公式以及推理的方向,帮助模型构建…...

计算机网络:什么是Mesh组网以及都有哪些设备支持Mesh组网?
Mesh组网技术详解与实现工具推荐 Mesh组网是一种通过多个节点路由器协同工作,形成覆盖全屋的无线网络的技术。它通过动态路径调整、无缝漫游和自愈能力,解决传统单一路由器覆盖不足的问题,尤其适合大户型、多层住宅或复杂户型环境。以下是Mesh组网的核心原理、实现方式及推…...

【阿里云免费领取域名以及ssl证书,通过Nginx反向代理web服务】
文章目录 前言一、申请域名1.1 访问阿里云官网1.2 输入自定义域名1.3 创建个人模板1.4 支付1元可以使用域名1年1.5 按照提示实名认证1.6 实名认证成功 二、域名解析2.1 选择域名解析2.2 解析设置2.3 快速添加解析2.4 选择对应类型2.5 解析成功 三、申请免费ssl证书3.1 访问阿里…...
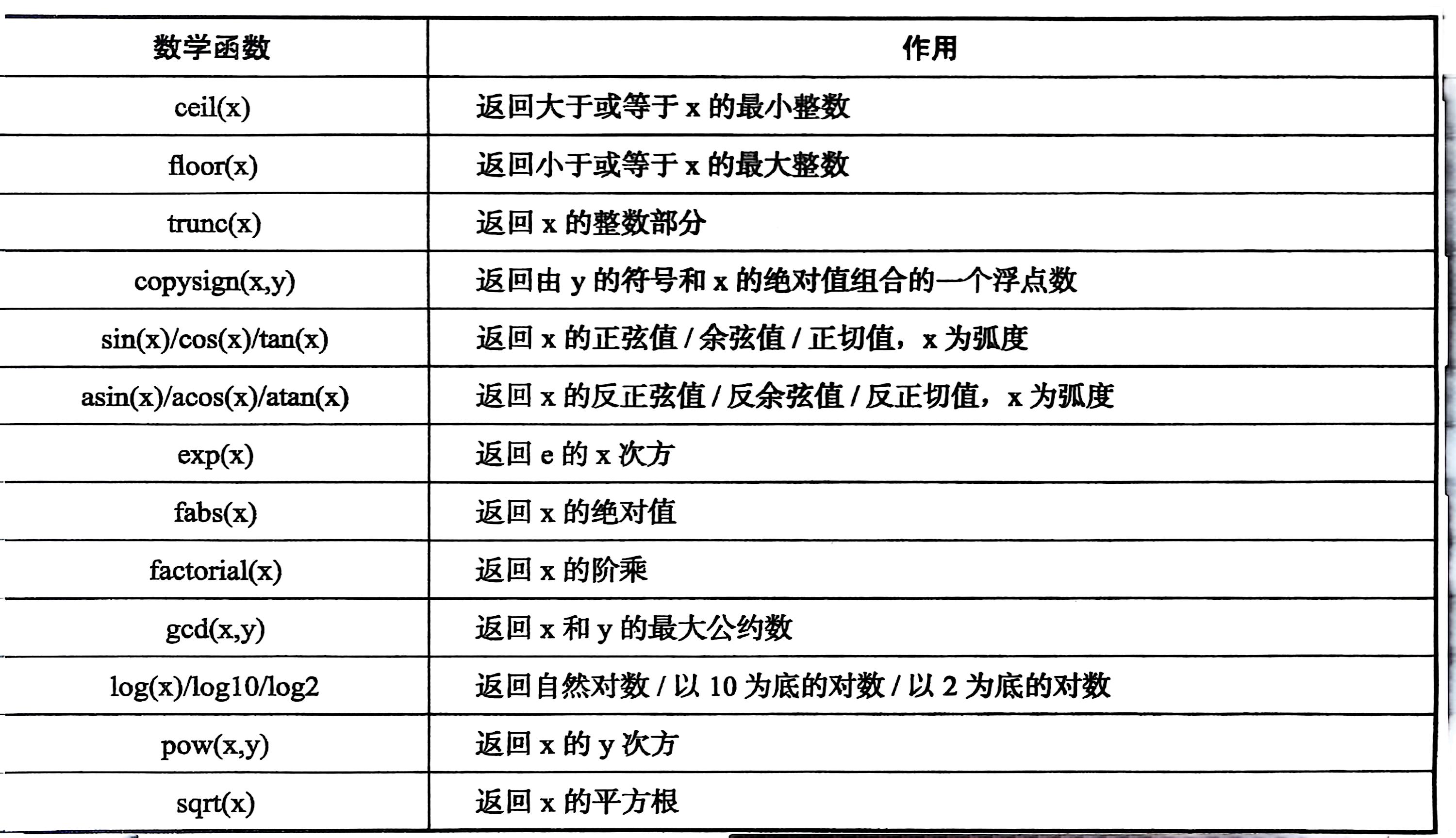
数据分析2
五、文件 CSV Comma-Separated Value,逗号分割值。CSV文件以纯文本形式存储表格数据(数字和文本)。 CSV记录间以某种换行符分隔,每条记录由字段组成,字段间以其他字符或字符串分割,最常用逗号或制表符。…...

实战项目5(08)
目录 任务场景一 【r1配置】 【r2配置】 【r3配置】 任务场景二 【r1配置】 【r2配置】 任务场景一 按照下图完成网络拓扑搭建和配置 任务要求: 通过在路由器R1、R2和R3上配置静态路由,实现网络中各终端PC能够正常…...

CSS结构性伪类、UI伪类与动态伪类全解析:从文档结构到交互状态的精准选择
一、结构性伪类选择器:文档树中的位置导航器 结构性伪类选择器是CSS中基于元素在HTML文档树中的层级关系、位置索引或结构特征进行匹配的一类选择器。它们无需依赖具体的类名或ID,仅通过文档结构即可精准定位元素,是实现响应式布局和复杂文档…...

.NET MAUI 基础知识
文章目录 什么是 .NET MAUI?MAUI的核心特点与Xamarin.Forms的区别 开发环境搭建安装Visual Studio 2022安装必要组件配置Android开发环境配置iOS开发环境验证安装 创建第一个MAUI应用创建新项目MAUI项目结构解析理解关键文件运行应用程序简单修改示例使用热重载 MAU…...
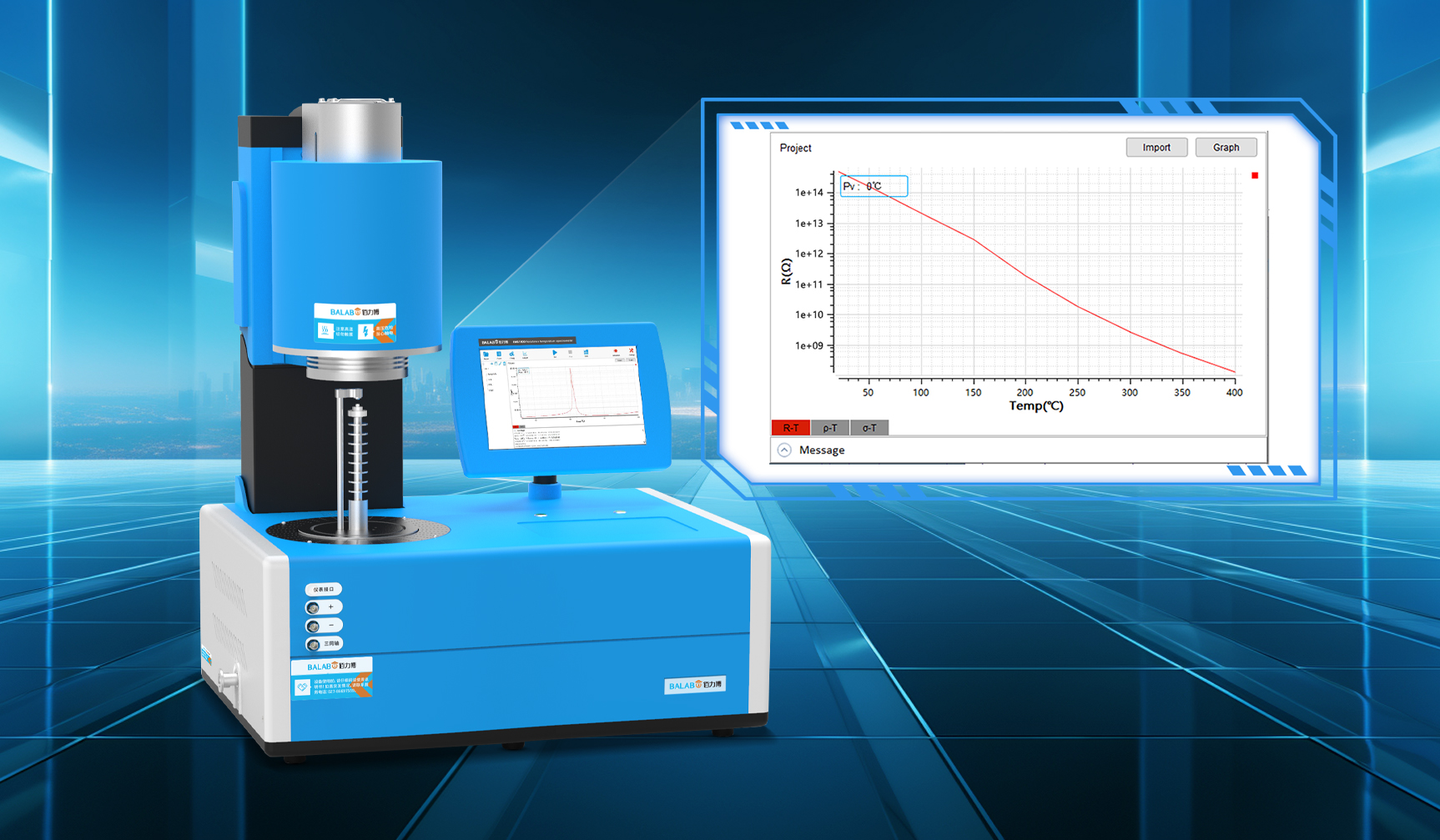
佰力博科技与您探讨表面电阻的测试方法及应用领域
表面电阻测试是一种用于测量材料表面电阻值的技术,广泛应用于评估材料的导电性能、静电防护性能以及绝缘性能。 1、表面电阻的测试测试方法: 表面电阻测试通常采用平行电极法、同心圆电极法和四探针法等方法进行。其中,平行电极法通过在试样…...

鹅厂面试数学题
题目 一个圆上随机取三个点,求这三个点构成锐角三角形的概率。 解答 根据圆周角定理,此题目等价为:一条线段长度为1的线段随机取两个点分成三段,任意一段长度均不大于1/2的概率。记前两段的长度为,则第三段的长度为…...

GO语言-导入自定义包
文章目录 1. 项目目录结构2. 创建自定义包3. 初始化模块4. 导入自定义包5. 相对路径导入 在Go语言中导入自定义包需要遵循一定的目录结构和导入规则。以下是详细指南(包含两种方式): 1. 项目目录结构 方法1:适用于Go 1.11 &#…...

java基础-package关键字、MVC、import关键字
1.package关键字: (1)为了更好管理类,提供包的概念 (2)声明类或接口所属的包,声明在源文件首行 (3)包,属于标识符,用小写字母表示 ࿰…...

[6-2] 定时器定时中断定时器外部时钟 江协科技学习笔记(41个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 V 30 31 32 33 34 35 36 37 38 39 40 41...

第五节:对象与原型链:JavaScript 的“类”与“继承”
📌 第五节:对象与原型链:JavaScript 的“类”与“继承” 目标:理解对象创建、原型继承、this 绑定,掌握类语法与原型设计模式,实现模块化组件开发。 一、对象基础:数据的“容器” 1. 对象字面…...
)
本地的ip实现https访问-OpenSSL安装+ssl正式的生成(Windows 系统)
1.下载OpenSSL软件 网站地址:Win32/Win64 OpenSSL Installer for Windows - Shining Light Productions 安装: 一直点击下一步就可以了 2.设置环境变量 在开始菜单右键「此电脑」→「属性」→「高级系统设置」→「环境变量」 在Path 中添加一个: xxxx\OpenSSL-…...

Spring Boot + MyBatis-Plus 高并发读写分离实战
引言 在高并发场景下,单一数据库实例往往成为性能瓶颈。数据库读写分离通过将读操作和写操作分配到不同的数据库实例,有效缓解主库压力,提升系统吞吐量。MyBatis-Plus 作为一款强大的持久层框架,结合 Spring Boot 能够轻松实现读…...
)
HarmonyOS 【诗韵悠然】AI古诗词赏析APP开发实战从零到一系列(二、项目准备与后台服务搭建)
在开发一款面向HarmonyOS平台的应用程序——【诗韵悠然】AI古诗词赏析APP时,选择了流行Go语言作为后端开发语言,并使用了go-zero微服务框架来搭建服务接口。本文将详细介绍项目准备和后台服务搭建的过程,帮助大家更好地理解和掌握go-zero框架…...

【PmHub后端篇】PmHub中基于自定义注解和AOP的服务接口鉴权与内部认证实现
1 引言 在现代软件开发中,尤其是在微服务架构下,服务接口的鉴权和内部认证是保障系统安全的重要环节。本文将详细介绍PmHub中如何利用自定义注解和AOP(面向切面编程)实现服务接口的鉴权和内部认证,所涉及的技术知识点…...
