牛客练习赛138(首篇万字题解???)
赛时成绩如下:

1. 小s的签到题
小s拿到了一个比赛榜单,他要用最快的速度找到签到题,但是小s脑子还是有点晕,请你帮帮小s,助力他找到签到题。
比赛榜单是一个 2 行 n 列的表格:
第一行是 n 个大写字母,代表题号;
第二行是 n 个字符串,对应每一道题目的通过人数和提交人数,字符串由两个整数构成,整数之间使用字符 ‘/’ 隔开。
我们定义,通过人数最多的题目是签到题。请你找到签到题的题号并输出。特别地,如果有多个签到题,输出题号字母表顺序最小的那道。输入描述:
第一行输入一个正整数 n(2≤n≤26),表示题目数量。
第二行输入 n 个两两不同的大写字母,表示每一道题的题号。
第三行输入 n 个字符串,表示每一道题的通过人数和提交人数。每个字符串格式为 a/b,其中 a 表示通过人数,b 表示提交人数。保证 0≤a≤b≤10^9
输出描述:
输出一个大写字母,表示签到题的题号。
示例1
输入
11
A B C D E F G H I J K
116/212 3/12 117/282 15/35 90/419 7/44 83/446 48/150 35/229 25/116 5/10
输出
C
解题思路:只需要比较a的大小, 然后记录下标, 输出A相对于下标的偏移量后字符即可(其实第二行输入没什么用)
#include <bits/stdc++.h>
using namespace std;
int main(){int n;cin >> n;vector<char> ids(n);for(int i = 0; i < n; i++){cin >> ids[i];}string s=""; int maxIdx=0;cin>>s;long long pos=s.find('/');string a=s.substr(0,pos);for(int i=1;i<n;i++){cin>>s;long long pos=s.find('/');string tmp=s.substr(0,pos); //字符串比较的是字典序而非大小if(stoll(tmp)>stoll(a)){a=tmp;maxIdx=i;}}cout<<(char)('A'+maxIdx)<<endl;return 0;
}2. 行列改写
题目描述
小柒最近获得了一个长度为 n 的数组 {r1,r2,…,rn} 和一个长度为 m 的数组 {c1,c2,…,cm}。他想用这两个数组来生成一个 n 行 m 列的二维数组,初始时,二维数组中每个元素的值均为 0,随后,他一共会进行 n+m 次操作,每次操作从以下两种覆盖方式中选择一种进行:
行覆盖:选择一个未被选中过的行,记为 i,将第 i 行的所有元素变为 ri;
∙列覆盖:选择一个未被选中过的列,记为 j,将第 j 列的所有元素变为 cj。
小柒希望最终的二维数组中所有元素之和最大,请你帮他计算这个最大值。输入描述:
第一行输入两个正整数 n,m(1≤n,m≤105)代表 r 数组和 c 数组的长度。
第二行输入 n 个正整数 r1,r2,…,rn(1≤ri≤106)代表 r 数组的数值。
第三行输入 m 个正整数 c1,c2,…,cm(1≤ci≤106)代表 c 数组的数值。
输出描述:
输出一个整数,代表最终的二维数组中所有元素之和的最大值。
示例1
输入
3 3
1 2 3
1 2 3
输出
22
解题思路: 初始时, 为一个n*m的二维数组, 最多操作m+n次, 选中第i行, 该行所有元素变为ri, 选中第j列, 该列所有元素变为cj, 对于每个格子(i,j), 最终的值取决于最后一次覆盖它的操作, 如果最终是行覆盖就为ri, 列覆盖的话就为cj, 行/列的顺序是无所谓的, 对于每一行来说, 我们先用行覆盖, 如果列覆盖有更优的, 我们再用列覆盖进行调整, 代码实现上, 我们先对c数组进行排序, 在遍历r数组的同时, 去c数组中找到第一个>r[i]的数, 那么它左侧的元素就用ri(行覆盖), 右侧的数就用cj(列覆盖), (右侧是连续数组, 我们可以用前缀和进行统计), 单行的总和就为
k*r[i]+(prefix[m]-prefix[k])
可以有人会有疑问,那如果我在第一行我用列覆盖,那在考虑第二行的时候, 会不会受影响啊?
其实是不会的, 这就是我上面的提到的行/列顺序是没有顺序的, 第二行覆盖在第一行的列覆盖之前操作,就解决了这个问题 (这题有点硬控我啊)
#include <bits/stdc++.h>
using namespace std;
int main(){int n, m;cin >> n >> m;vector<int> a(n), b(m);for(int i = 0; i < n; i++) cin >> a[i];for(int i = 0; i < m; i++) cin >> b[i];sort(b.begin(), b.end());vector<long long> prefix(m + 1, 0);for(int j = 0; j < m; j++){prefix[j + 1] = prefix[j] + b[j];}long long total_B = prefix[m];long long ans = 0;for(int i = 0; i < n; i++){int k = upper_bound(b.begin(), b.end(), a[i]) - b.begin();ans += (long long)k * a[i] + (total_B - prefix[k]);}cout << ans << endl;return 0;
}
3. 树上替身追赶游戏
本题与《E.图上替身追赶游戏》共享部分题目背景,我们建议您重新阅读题面。
给定一棵由 n 个点和 n−1 条边组成的树,结点编号为 1∼n。Saki 和 Miku 在树上的点之间移动,模拟追赶游戏,初始时两个人都在节点 k。
游戏分若干回合进行,由你扮演 Saki。每回合包含以下步骤:
1.Saki 移动:记回合开始时 Saki(你)在节点 a,你必须选择一个与 a 相邻的节点 b 并移动至 b;
2.Saki 放置替身:Saki(你)不想被 Miku 追上,所以你必须选择一个与节点 b 相邻的节点 c 放置一个替身,该替身仅在本回合内存在;
3.Miku 追赶:Miku 将替身视为 Saki 的位置并据此行动:
若 Miku 本就位于替身所在的节点 c,她停留不动;
否则,Miku 在其当前节点的相邻节点中,选择到节点 c 距离最近的节点 d 并移动到该节点(换句话说,点 d 是 Miku 所在的位置到点 c 的最短路径中的下一个节点)。
游戏在 Saki 首次移动后开始计为第 1 回合。如果在任何时刻 Saki 与 Miku 重合,游戏立即结束。
请计算,如果你采取最优策略,最多能够将游戏进行到第几回合?输入描述:
第一行输入两个正整数 n,k(2≤n≤105; 1≤k≤n),表示树的结点数、双方起始位置。此后 n−1 行,第 iii 行输入两个整数 ui,vi(1≤ui,vi≤n),表示第 i 条树边连接第 ui 个点和第 vi 个点。保证给定的边构成一棵树。
输出描述:
输出一个整数,表示 Saki 最多能够坚持到第几回合结束。
示例1
输入
5 1
1 2
1 3
1 4
1 5
输出
2
在这个样例中,其中一种最优策略的移动状况如下:1.Saki 移动到 2 号结点;
2.Saki 在 1 号结点放置替身;
3.Miku 停留不动。
第二回合:
1.Saki 移动到 1号结点。
此时,她与 Miku 重合,游戏结束。
我们可以证明,不存在比 2 回合坚持更久的策略。
解题思路: 看不懂题意的,可以直接看样例画个图, 求(重合)能坚持多少个回合
Saki 应该尽可能往远离 Miku 的方向跑,即往树的最深处跑
因为树的直径决定了 Saki 最多能跑多远代码实现上:
计算 Miku 的最短距离(d_M):
从初始点 k 出发,BFS 计算 Miku 到所有节点的最短距离
计算 Saki 的最短距离(d_S):
Saki 每回合可以移动一步,但必须保证 d_S[u] + 1 <= d_M[v](即 Saki 不能跑到 Miku 已经能更快到达的地方)
最大回合数:
Saki 能跑的最远距离 max_d,回合数 = max_d + 1(因为第 max_d 步时 Miku 会追上)
#include <bits/stdc++.h>
using namespace std;
int main(){int n, k;cin >> n >> k;vector<vector<int>> a(n+1);for(int i = 1, x, y; i < n; i++){cin >> x >> y;a[x].push_back(y);a[y].push_back(x);}vector<int> d_M(n+1, -1);queue<int> p;d_M[k] = 0;p.push(k);while(!p.empty()){int u = p.front(); p.pop();for(int v : a[u]){if(d_M[v] == -1){d_M[v] = d_M[u] + 1;p.push(v);}}}vector<int> d_S(n+1, -1);long long max_d = 0;queue<int> q;d_S[k] = 0;q.push(k);while(!q.empty()){int u = q.front(); q.pop();for(int v : a[u]){if(d_S[v] == -1 && d_S[u] + 1 <= d_M[v]){d_S[v] = d_S[u] + 1;max_d = max<long long>(max_d, d_S[v]);q.push(v);}}}cout << (max_d + 1) << endl;return 0;
}
4. 全对!
题目链接:登录—专业IT笔试面试备考平台_牛客网
小 S 有 n 个对错机器人,每个对错机器人的行为逻辑由一个长度不超过 16,仅由字符 ‘0’ 和 ‘1’ 构成的字符串表示。在本题中,我们记字符串的下标从 1 开始。
对于第 i 个机器人,记其初始字符串为 si,其会先将这个字符串无限重复拼接成一个无限长的循环字符串 si∞。随后,对于第 j 时刻,它会根据si∞ 的第 j 个字符来决定回答「对的」还是「不对」:
∙ ,∙如果 si∞ 的第 j 个字符为 ‘1’,则表示第 i 个机器人在第 j 秒回答「对的」;
∙,∙如果 si∞ 的第 j 个字符为 ‘0’,则表示第 i 个机器人在第 j 秒回答「不对」。
更具体地,如果某个机器人的初始字符串是 "10101" ,那么这个机器人会在第 1,3,5,6,8,10,11,… 秒回答「对的」,在第 2,4,7,9,12,… 秒回答「不对」。
请问是否存在一个时刻 t,使得所有机器人在第 t 秒都回答「对的」,这样的时刻被称为「全对时刻」。如果存在,输出最小的「全对时刻」;否则,输出 −1。
解题思路:
举个例子:
3
001
0110
100013个字符串都是无限循环的,
001001001001001...
0110011001100110....
100011000110001...
输出第一个全是1的时刻, 就是 6
往&运算上面思考(相同位置是1, '与'完仍然是1)即可, 模拟思路即可
代码实现上, 由于单个字符串(在不无限循环情况下)不会超过16,
对于每个长度为L的字符串, 我们需要记录每个位置r是否都为1,
eg:
110
101
111
b[0]=1, b[1]=0, b[2]=0
a[3][0]=1, a[3][1]=0, a[3][2]=0
a[L][r]: 表示长度为L的字符串在第r个位置是否全为1
接着枚举时间t , 需要找到最小额的t, 使得对于所有 L(1~16), t % L 对应的位置 r 满足 a[L][r] = true
eg: 解释一下这个% ,如果t=5, L=3, 5%3=2,检查a[3][2]是否为true, L=4, 5%4=1, 检查a[4][1]是否为 true, 如果所有L都满足, 那么t=5就是一个解, 没有解就输出-1。
#include <bits/stdc++.h>
using namespace std;
const int M = 1000000;
int main(){int n; cin>>n;vector<vector<bool>> a(17);for(int i=1;i<=16;i++){a[i].resize(i,true);}for(int i = 0; i < n; i++){string s;cin >> s;int L = s.size();vector<bool> b(L, false);for(int r = 0; r < L; r++){if(s[r] == '1')b[r] = true;}for(int r = 0; r<L;r++){a[L][r] = a[L][r] & b[r];}}for(int l = 1; l <= 16; l++){bool f = false;for(bool x : a[l]) if(x){ f = true; break; }if(!f){cout << -1 << endl;return 0;}}for(int t = 1; t <= M; t++){bool f = true;for(int l= 1; l<=16;l++){int r = (t-1)%l;if(!a[l][r]){f = false;break;}}if(f){cout << t << endl;return 0;}}cout << -1 << endl;return 0;
}5. 图上替身追赶游戏
为了甩开 Miku,你可以在游戏开始前发动一次「神之力」:在这棵树上选择不相邻的两个点 u,vu,随后在这两点之间加一条边,使得树变成一个无向图,随后,游戏在图上进行!特别地,这样操作后,如果 Miku 有多个满足条件的点选择,那么她一定会选择下标最小的那个并进行移动。
求解,有多少种不同的「神之力」施展方法,使得 Saki(你)可以在神之力发动后,通过一系列操作,在某个回合结束时,可以和 Miku 不相邻、不重合。【注意】
与《C.树上替身追赶游戏》不同的是,在本题中,任何时刻 Saki 和 Miku 重合,游戏都不会结束。
在 u,v 加边和在 v,u加边被视为同一种「神之力」施展方法。更具体地,如果两次「神之力」选择的点相同,视为同一种加边方法。输入描述:
第一行输入两个正整数 n,k(2≤n≤105; 1≤k≤n),表示树的结点数、双方起始位置。
此后 n−1 行,第 iii 行输入两个整数ui,vi(1≤ui,vi≤n),表示第 i 条树边连接第 ui 个点和第 vi个点。保证给定的边构成一棵树。
输出描述:
输出一个整数,表示有多少种不同的「神之力」施展方法。此题是第三题的修改版
解题思路:树形DP,比赛的时候看F题题目挺短的, 就直接写F题, 这题没看
可以通过手玩一下样例发现,树在加边后会产生一个环,这个环是saki甩开miku的关键。当环的长度分别为4、5、6时,均可以通过一系列操作,使得在某个回合结束时,与miku不再相邻或重合。
也就是说本题可以转化为,计算给定树中长度为3、4和5的简单路径的总数量。代码采用树形动态规划(Tree DP)的思想来解决。
核心思路:
我们通过深度优先搜索(DFS)遍历树,并在DFS的过程中计算和累积路径信息。关键在于定义DP状态以及如何合并子树信息。
其中变量 ans 最终累计了所有长度为3、4、5的简单路径的数量。通过一次DFS遍历,利用 f[d][u] 数组存储子树内距离信息。在回溯时(即子节点DFS结束后),它首先利用当前 f[j][u](代表“左侧分支”)和 f[k-j][v](代表“右侧分支”,其中 v 是刚处理完的子节点)来组合路径并更新 ans,然后才将 v 子树的信息整合进 f[][u],为后续的计算做准备。这种“先计算贡献,再合并信息”的顺序是树形DP中常见的处理方式,确保了每个路径只被计算一次且不会遗漏。
代码
1. DP状态定义:
f[k][u]:表示在以节点 u 为根的子树中,与节点 u 距离为 k 的节点有多少个。
2. DFS过程详解:
dfs(u, fa) 函数处理以 u 为当前节点,fa 为其父节点的情况。
初始化:
dep[u] = dep[fa] + 1:计算当前节点 u 的深度(根节点深度为1,其父节点0的深度为0)。
f[0][u] = 1:对于节点 u 本身,它与自身的距离为0。所以以 u 为根的子树中,与 u 距离为0的节点只有 u 自己,数量为1。
遍历子节点: 对于 u 的每个子节点 v(v != fa):递归调用: dfs(v, u)。这会先计算完成以 v 为根的子树中所有的 f[][v] 值。
路径统计 (核心部分): 在从 dfs(v, u) 返回后,我们利用已经计算好的 f[][u](包含 u 自身以及 u 的 在 v 之前处理过的 其他子树的信息)和 f[][v](包含 v 的子树信息)来统计经过边 (u,v) 的路径。 我们关注的路径形态是 X - ... - u - v - ... - Y,其中:
X 是在 u 的子树中(但在 v 的子树之外,或者是 u 本身)的一个节点。
Y 是在 v 的子树中的一个节点。
路径 X - ... - u 的长度为 j。这样的 X 有 f[j][u] 个。
路径 v - ... - Y 的长度为 d。这样的 Y 有 f[d][v] 个。
那么,完整路径 X - ... - u - v - ... - Y 的长度为 j + 1 + d (1代表边 (u,v) 的长度)。
代码中的循环 k->(2, 5): 实际上是在枚举 j+d 的值。当 k = 2时,我们统计 j+d = 2,总路径长度为 j+d+1 = 3。
当 k = 3时,我们统计 j+d = 3,总路径长度为 j+d+1 = 4。
当 k = 4时,我们统计 j+d = 4,总路径长度为 j+d+1 = 5。
内层循环 j->(0, k + 1): 枚举了路径 X - ... - u 的长度 j (即 d1)。那么路径 v - ... - Y 的长度 d (即 d2) 就必须是 k-j。
此时,符合条件的路径数量为 f[j][u] * f[k-j][v]。将这个乘积累加到 ans。
注意:这里的 f[j][u] 尚未包含来自子树 v 的贡献,这正是我们想要的,因为它保证了路径的两个分支分别来自 u 的不同“方向”(一个方向是 v 子树,另一个方向是 u 的其他子树或 u 自身)。
更新 f[][u]: 在统计完以 v 为一支的路径后,需要将子树 v 的信息合并到 f[][u] 中,以便后续 u 的其他兄弟子树或者 u 的父节点使用。 j-> (0,5): f[j + 1][u] += f[j][v] 这条语句的含义是: 如果一个节点 Z 在子树 v 中,且与 v 的距离为 j(这样的节点有 f[j][v] 个),那么节点 Z 与 u 的距离就是 j+1。 所以,我们将 f[j][v] 的值累加到 f[j+1][u] 上。 j 从0到4,意味着 j+1 从1到5。这对应了 f 数组的维度。DFS起始: dfs(1, 0) 从节点1开始DFS,假设节点0是节点1的虚拟父节点,其深度为0。
#include <bits/stdc++.h>
using namespace std;
int n, _;
vector<vector<int>> g;
vector<vector<long long>> f;
long long ans;
vector<int> dep;
void dfs(int u, int fa) {dep[u] = dep[fa] + 1;f[0][u] = 1;for (int v : g[u]) {if (v == fa) continue;dfs(v, u);for (int k = 2; k <= 4; ++k) {for (int j = 0; j <= k; ++j) {ans += f[j][u] * f[k - j][v];}}for (int j = 0; j < 5; ++j) {f[j + 1][u] += f[j][v];}}
}int main() {cin >> n >> _;g.assign(n + 1, {});for (int i = 0; i < n - 1; ++i) {int u, v;cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}f.assign(6, vector<long long>(n + 1, 0));dep.assign(n + 1, 0);ans = 0;dfs(1, 0);cout << ans << endl;return 0;
}6.素数回路
给定偶数 n,构造一个由1∼n 这 n 个不同的整数构成环形数组 a,使得相邻两项的差均为奇素数。
奇素数是指除了 2 以外的素数,最小的四个奇素数是 3,5,7,11输入描述:
每个测试文件均包含多组测试数据。第一行输入一个整数 T(1≤T≤105) 代表数据组数,每组测试数据描述如下:
在一行上输入一个偶数 n(2≤n≤10^5)。
除此之外,保证单个测试文件的 n 之和不超过 2×10^5。
输出描述:
对于每一组测试数据,新起一行。如果不存在合法的环形数组,直接输出 −1。否则,输出 n个整数,表示构造的环形数组 a。
你需要保证数组 a 是一个由 1∼n1 这 n 个不同的整数组成的数组,下标从 0 开始,满足任取 0≤i<n,∣ai−a(i+1) mod n∣均为奇素数。
解题思路:输入n,ai→[1,n], 排列满足相邻差是一个奇素数(除了2的素数)
我们从1开始考虑,如果n是奇数,例如n=5, 满足题意的就是 1→4, 连不起,
...n=7, 满足题意的就为1 4 7 2 (从1开始,每次考虑3或者5),还是不行,
n=8, 满足题意的就为1 4 7 2 5 8 3 6
n=9, 1 → 4 → 7 → 2 → 5 → 8 → 3 → 6 → 9 → 1 最后一步不行
观察可以得出, ai=1, 加上一个奇素数,就会变成偶数, 再加上一个奇素数就会变成奇数, 如果n是奇数, 最后一步就会变成奇数, 奇数-奇数=偶数, 就回不到起始点了
接下来,我们先将奇素数预处理一下,存到o_p这个数组中, 接着我们找一个奇素数p, 使得 n - p 也是奇素数(这个是观察出来的, 比如, n=8, n=10, n=12, 自己推导一下)
找到符合条件的p后,
构造环形数组:
使用公式:(cur - 1 + p) % n + 1 (eg: n=8)
cur=1 → (1-1+3)%8+1=4 → (4-1+3)%8+1=7 → (7-1+3)%8+1=2 → (2-1+3)%8+1=5 → (5-1+3)%8+1=8 → (8-1+3)%8+1=3 → (3-1+3)%8+1=6 → (6-1+3)%8+1=1。
最终数组:[1,4,7,2,5,8,3,6]。
检查相邻差:
|1-4|=3,|4-7|=3,|7-2|=5,|2-5|=3,|5-8|=3,|8-3|=5,|3-6|=3,|6-1|=5。
所有差都是奇素数,构造成功。(依旧硬控....)
#include <bits/stdc++.h>
using namespace std;
const int N = 200000;
int main(){vector<bool> is_prime(N+1, true);is_prime[0] = is_prime[1] = false;for(int i = 2; i*i <= N; i++){if(is_prime[i]){for(int j = i*i; j <= N; j += i){is_prime[j] = false;}}}vector<int> o_p;for(int i = 3; i <= N; i += 2){if(is_prime[i]) o_p.push_back(i);}int T;cin >> T;while(T--){int n;cin >> n;if(n < 8 || n % 2 != 0){cout << -1 << endl;continue;}int p = -1;for(int x : o_p){if(x >= n) break;int y = n - x;if(y >= 3 && is_prime[y]){p = x;break;}} if(p == -1){cout << -1 << endl;continue;}vector<int> ans;int cur = 1;for(int i = 0; i < n; i++){ans.push_back(cur);cur = (cur - 1 + p) % n + 1;}cout << ans[0];for(int i = 1; i < n; i++) cout << ' ' << ans[i];cout << endl;}return 0;
}7.k人训练方阵
吹奏部有 n 名部员,saki 作为吹奏部的一员,负责从 n 名部员中选择若干名部员组成「k 人方阵」来参加活动。这是指一个由吹奏部部员组成的表演方阵,首先必须有一个领队站在前面,方阵有若干排(可以 0排),但每排必须是 k 个人。
请你帮 Saki 计算一下有多少种不同的「k 人方阵」选法?由于答案可能很大,请将答案对 (109+7) 取模后输出。
注意 saki 只要选出若干名部员,能够组成「k 人方阵」就可以了,不需要去安排每个人的分工和站的位置,对是否是领队不作区分。
解题思路:组合数(快结束的时候, 套了一下板子, 超时了...)
#include <bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7;
const int MAXN = 1e7;
vector<long long> F, INV_fac;
int quPow(long long a, int n) {long long res = 1;while(n) {if(n & 1) res = res * a % MOD;a = a * a % MOD;n >>= 1;}return res;
}
void init(int MAXN) {F.resize(MAXN + 1,0);INV_fac.resize(MAXN + 1,0);F[0] = 1;for(int i = 1; i <= MAXN; i++)F[i] = F[i - 1] * i % MOD;INV_fac[MAXN] = quPow(F[MAXN], MOD - 2);for(int i = MAXN - 1; i >= 0; i--)INV_fac[i] = INV_fac[i + 1] * (i + 1) % MOD;
}
long long C(int n, int r) {if(r < 0 || r > n) return 0;return F[n] * INV_fac[r] % MOD * INV_fac[n - r] % MOD;
}
int main() {init(MAXN); int T;cin >> T;while(T--) {int n, k;cin >> n >> k;long long ans = 0;for(int r = 1; r <= n; r += k) {ans = (ans + C(n, r)) % MOD;}cout << ans << endl;}return 0;
}感谢大家的点赞和关注,你们的支持是我创作的动力!(其他细节,有时间再补充...)
相关文章:

牛客练习赛138(首篇万字题解???)
赛时成绩如下: 1. 小s的签到题 小s拿到了一个比赛榜单,他要用最快的速度找到签到题,但是小s脑子还是有点晕,请你帮帮小s,助力他找到签到题。 比赛榜单是一个 2 行 n 列的表格: 第一行是 n 个大写字母&#…...

Rust 中的 `String`、`str` 和 `str`:深入解析与使用指南
在 Rust 编程中,字符串是不可或缺的数据类型,但 Rust 的字符串系统与其他语言有所不同。Rust 提供了 String、str 和 &str 三种主要的字符串类型,每种类型都有其独特的用途和特点。本文将详细介绍这三种字符串类型,帮助你更好…...

深入理解高性能网络通信:从内核源码到云原生实践
深入理解高性能网络通信:从内核源码到云原生实践 (示意图:Linux网络协议栈与通信架构分层模型) 随着互联网业务规模的不断扩大,系统对网络通信性能的要求也在迅速提升。从内核事件机制的演进到云原生架构下的极致优化&…...

10 web 自动化之 yaml 数据/日志/截图
文章目录 一、yaml 数据获取二、日志获取三、截图 一、yaml 数据获取 需要安装 PyYAML 库 import yaml import os from TestPOM.common import dir_config as Dir import jsonpathclass Data:def __init__(self,keyNone,file_name"test_datas.yaml"):file_path os…...

ubuntu清除缓存
pip pip cache purgeconda conda clean -a -yapt apt cleanapt-get apt-get cleanmodelscope modelscope clear-cachehuggingface rm -rf ~/.cache/huggingface/*...

OSI 7层模型
OSI 7层模型: 1、物理层(光纤等把电脑连接起来的物理手段) 2、数据链路层(以太网,确认0和1电信号的分组方式,负责MAC地址,MAC地址用于在网络中唯一标示一个网卡,相当于网卡的身份证…...
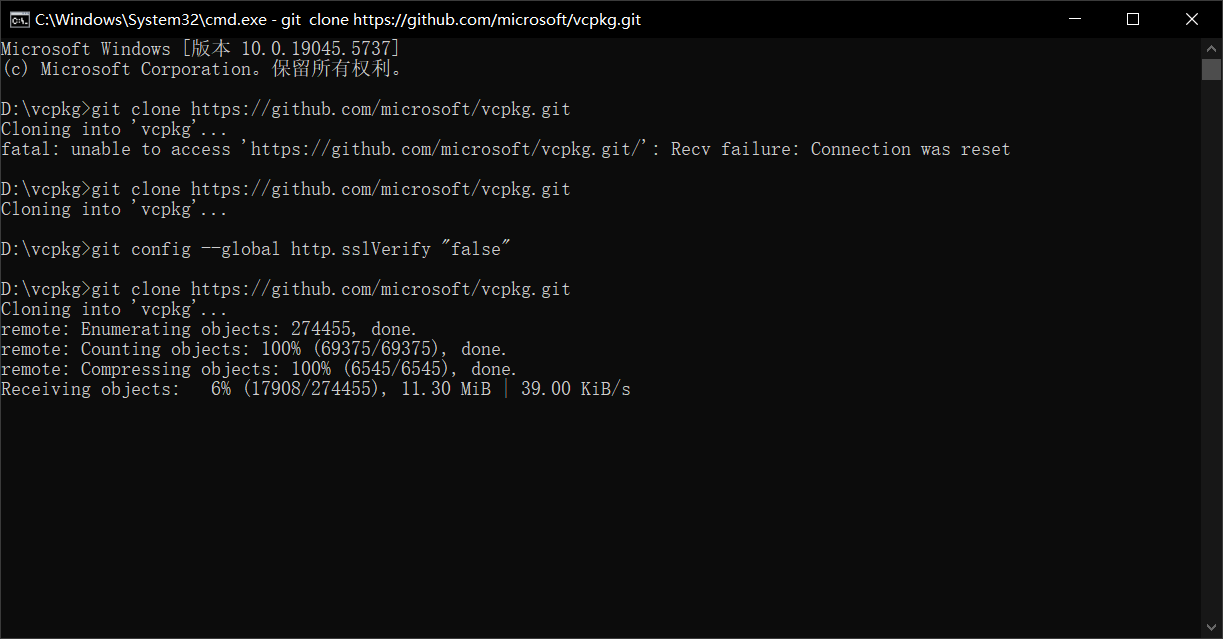
用git下载vcpkg时出现Connection was reset时的处理
用git安装vcpkg时出现Connect was rest(如上图)。多谢这位网友的博文解决了问题: 通过:http.sslVerify false全局来设置,执行以下命令: git config --global http.sslVerify "false" 原文链接:…...

deepseek梳理java高级开发工程师算法面试题
Java高级工程师算法面试题与答案 一、数据结构与算法基础 1. 红黑树与AVL树比较 题目:详细说明红黑树和AVL树的区别及各自的适用场景,并用Java实现红黑树的插入操作。 答案: 区别对比: ┌─────────────────…...

leetcode - 滑动窗口问题集
目录 前言 题1 长度最小的子数组: 思考: 参考代码1: 参考代码2: 题2 无重复字符的最长子串: 思考: 参考代码1: 参考代码2: 题3 最大连续1的个数 III: 思考&am…...

一分钟在Cherry Studio和VSCode集成火山引擎veimagex-mcp
MCP的出现打通了AI模型和外部数据库、网页API等资源,成倍提升工作效率。近期火山引擎团队推出了 MCP Server SDK: veimagex-mcp。本文介绍如何在Cherry Studio 和VSCode平台集成 veimagex-mcp。 什么是MCP MCP(Model Context Protocol&…...

Tomcat与纯 Java Socket 实现远程通信的区别
Servlet 容器(如 Tomcat) 是一个管理 Servlet 生命周期的运行环境,主要功能包括: 协议解析:自动处理 HTTP 请求/响应的底层协议(如报文头解析、状态码生成); 线程…...

为什么企业建站或独立站选用WordPress
与大多数组织相比,企业业务更需要保持可扩展和可靠的网络存在,以保持竞争力。为此,许多大型企业的 IT 领导者历来寻求昂贵的网络解决方案,这些方案需要签订专有支持合同来保证质量。不过,还有另一种方法。WordPress问世…...

镜头内常见的马达类型(私人笔记)
① 螺杆式马达 驱动来源:机身内马达。镜头尾部有一个接收“螺杆”的接口,通过机械传动带动镜头对焦组。缺点:慢、吵、不能用于无机身马达的相机。✅ 典型镜头:尼康 AF、AF-D 系列;美能达老镜头。尼康传统的AF镜头通过…...

docker-compose——安装mysql8
一、编写Dockerfile FROM mysql:8.0.39 ENV TZAsia/Shanghai RUN ln -sf /usr/share/zoneinfo/$TZ /etc/localtime && echo $TZ > /etc/timezone二、编写docker-compose.yml version : 3.8services:zaomeng-mysql:build:context: ./mysqlimage: mysql:8.0.39conta…...

从代码学习深度学习 - 语义分割和数据集 PyTorch版
文章目录 前言什么是语义分割?图像分割和实例分割Pascal VOC2012 语义分割数据集Pascal VOC2012 语义分割数据集介绍基本信息语义分割部分特点数据格式评价指标应用价值数据集获取使用提示辅助工具代码 (`utils_for_huitu.py`)读取数据预处理数据自定义语义分割数据集类读取数…...

4G物联网模块实现废气处理全流程数据可视化监控配置
一、项目背景 随着工业化进程的加速,工业废气的排放对环境造成了严重影响,废气处理厂应运而生。然而,废气处理厂中的设备众多且分散,传统的人工巡检和数据记录方式效率低下,难以及时发现问题。为了实现对废气处理设备…...

深圳SMT贴片加工厂制造流程解析
内容概要 作为大湾区电子制造产业链的重要节点,深圳SMT贴片加工厂凭借精密的生产体系与技术创新,构建了涵盖12道核心工序的标准化流程。从PCB基板的来料检验开始,通过全自动贴片机的高精度元件定位、SPI三维锡膏检测、智能温控回流焊接等关键…...

电商平台如何做好DDoS 攻防战?
一、新型 DDoS 攻击技术演进分析 1.1 电商平台面临的四类攻击范式 graph LR A[DDoS攻击] --> B{网络层} A --> C{应用层} B --> D[CLDAP反射攻击<br>峰值达3.5Tbps] B --> E[QUIC协议洪水攻击] C --> F[API CC攻击<br>精准打击抢购接口] C -->…...

Spark处理过程-转换算子
大家前面的课程,我们学习了Spark RDD的基础知识,知道了如何去创建RDD,那spark中具体有哪些rdd,它们有什么特点呢? 我们这节课来学习。 (一)RDD的处理过程 Spark使用Scala语言实现了RDD的API,程…...

【计算机视觉】OpenCV实战项目:Athlete-Pose-Detection 运动员姿态检测系统:基于OpenCV的实时运动分析技术
运动员姿态检测系统:基于OpenCV的实时运动分析技术 1. 项目概述1.1 技术背景1.2 项目特点 2. 技术架构与算法原理2.1 系统架构2.2 核心算法2.3 模型选择 3. 项目部署与运行指南3.1 环境准备硬件要求软件依赖 3.2 项目配置3.3 运行项目基本运行模式高级参数 4. 常见问…...

Java 性能调优全解析:从设计模式到 JVM 的 7 大核心方向实践
引言 在高并发、低延迟的技术场景中,Java 性能优化需要系统化的方法论支撑。本文基于7 大核心优化方向(复用优化、计算优化、结果集优化、资源冲突优化、算法优化、高效实现、JVM 优化),结合权威框架与真实案例,构建从…...

为什么要选择七彩喜数字康养平台?加盟后有何优势?
一.七彩喜数字康养平台 1.技术领先性 七彩喜依托“端-网-云-脑”四层技术架构,整合毫米波雷达、AI算法引擎、区块链等前沿技术,解决传统养老的隐私泄露、设备孤岛等痛点。 比如非接触式健康监测系统通过毫米波雷达实现跌倒检测准确率&#…...

【计算机视觉】OpenCV实战项目:基于OpenCV的车牌识别系统深度解析
基于OpenCV的车牌识别系统深度解析 1. 项目概述2. 技术原理与算法设计2.1 图像预处理1) 自适应光照补偿2) 边缘增强 2.2 车牌定位1) 颜色空间筛选2) 形态学操作3) 轮廓分析 2.3 字符分割1) 投影分析2) 连通域筛选 2.4 字符识别 3. 实战部署指南3.1 环境配置3.2 项目代码解析 4.…...
鸿蒙接入flutter环境变量配置windows-命令行或者手动配置-到项目的创建-运行demo项目
鸿蒙接入flutter环境变量配置 参考官网 下载flutter git clone https://gitcode.com/openharmony-sig/flutter_flutter.git git checkout -b dev origin/dev # 国内镜像 export PUB_HOSTED_URLhttps://pub.flutter-io.cn export FLUTTER_STORAGE_BASE_URLhttps://storage.fl…...

Flink CDC—实时数据集成框架
Flink CDC 是一个基于流的数据集成工具,旨在为用户提供一套功能更加全面的编程接口(API),它基于数据库日志的 CDC(变更数据捕获)技术实现了统一的增量和全量数据读取。 该工具使得用户能够以 YAML 配置文件…...

Redis的持久化:RDB和AOF机制
概述 Redis 提供 RDB 和 AOF 两种持久化机制,它们在数据安全性、性能、恢复速度等方面有显著差异。 为什么要进行持久化?如果是大数据量的恢复,会有下述的影响 会对数据库带来巨大的压力,数据库的性能不如Redis。导致程序响应慢…...

微调ModernBERT为大型语言模型打造高效“过滤器”
ModernBERT(2024 年 12 月)是最近发布的小型语言模型,由 Answer.AI、LightOn 和 HuggingFace 共同开发。它利用了现代优化技术,如用于 8,192 token 上下文窗口的 RoPE 和 GeGLU layers,在保持效率的同时提升性能。jina…...

数据库查询中的分页实现:Page对象与Pageable接口详解
文章目录 前言1. 分页查询的核心概念1.1 Page对象1.2 Pageable接口2. 实现代码详解2.1 实体类定义2.2 Repository接口定义2.3 服务层实现2.4 控制器层实现3. 关键点解析3.1 Pageable对象的创建3.2 Page对象的常用方法3.4 错误用法示例4.完整示例输出4.1 基本分页查询输出4.2 条…...

各大编程语言基本语法区别
1:语言特点 函数式语言和面向对象语言的区别:函数式用函数直接进行操作,面向对象用object.method()进行操作;如:len() <=> object.length() C 语言:1)C 语言可以像汇编语言一样对位、字节和地址进行操作;2)有函数原型;3)具有大量的数值类型;4)函数是C语言…...

云计算中的虚拟化:成本节省、可扩展性与灾难恢复的完美结合
云计算中虚拟化的 4 大优势 1. 成本效益 从本质上讲,虚拟化最大限度地减少了硬件蔓延。团队可以将多个虚拟机整合到单个物理主机上,而不是为每个工作负载部署单独的服务器。这大大减少了前期硬件投资和持续维护。 结果如何?更低的功耗、更低…...
