和为target问题汇总
文章目录
- 习题
- 377.组合总和 IV
- 494.目标和
- 和为
target的问题,可以有很多种问题的形式的考察,当然,及时的总结与回顾有利于我们熟练掌握这些知识!
习题
377.组合总和 IV
377.组合总和 IV


- 思路分析:通过观察,由于
nums数组里面的元素可以重复选择,并且没有数量限制,所以这个题目就是一个有len(nums)个选择的爬楼梯问题,所以我们就是使用爬楼梯问题模版进行解决 - 总体的时间复杂度是
o(n*target)
class Solution:def combinationSum4(self, nums: List[int], target: int) -> int:# 动态规划的问题,nums[i]中为你每一步可以选择的步伐大小# 定义dp[i]表示到达i的方案数,那么就可以由先前的位置转移而来dp = [1]+[0]*targetfor i in range(1,target+1):cou = 0for j in nums:if i - j >= 0:cou += dp[i-j]dp[i] = coureturn dp[target]
494.目标和
494.目标和


- 思路分析:
- 这是一个
子序列和为target的问题,需要定义dp[i][j]为前i个数字中,对应和为j的方案数,所以我们需要使用一个二重循环进行求解 - 当然这题就是需要转换一下
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:# 类似于0-1背包问题,求解的是运算结果等于target的表达式的数目# 我们可以照常选择正数zheng,那么对应的负数就是sum(nums) - zheng# dp[i][j] 定义为前i个数字中,值为j的数目# dp[i][j] = dp[i-1][j-nums[i]] + dp[i-1][j+nums[i]] ,计算nums[i]=0也没关系,+,-0算两个表达式# 那么dp数组怎么开这个target,原本的困惑,就是选了正数还要管这个target的范围# 由式子,选取正数的和为p,要减去的数字和为q,有p+q=s,p-q = target,就可以求解出p与q的值即可# 我们只要开的空间等于其中一个即可,也可以去一个绝对值都算上s = sum(nums) - abs(target)if s<0 or s%2 == 1:return 0m = s // 2n = len(nums)dp = [[0]*(m+1) for _ in range(n+1)]# 赋初值为1,不然后面算不了dp[0][0] = 1for i in range(n):for j in range(m+1):if j < nums[i]:dp[i+1][j] = dp[i][j]else:# dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]dp[i+1][j] = dp[i][j] + dp[i][j-nums[i]]return dp[n][m]
相关文章:

和为target问题汇总
文章目录 习题377.组合总和 IV494.目标和 和为target的问题,可以有很多种问题的形式的考察,当然,及时的总结与回顾有利于我们熟练掌握这些知识! 习题 377.组合总和 IV 377.组合总和 IV 思路分析:通过观察࿰…...

STM32单片机内存分配详细讲解
单片机的内存无非就两种,内部FLASH和SRAM,最多再加上一个外部的FLASH拓展。在这里我以STM32F103C8T6为例子讲解FLASH和SRAM。 STM32F103C8T6具有64KB的闪存和20KB的SRAM。 一. Flash 1.1 定义 非易失性存储器,即使在断电后,其所…...

RedHat7 如何更换yum镜像源
RedHat7如何更换yum镜像源? # 删除系统自带 yum rpm -qa|grep -e yum -e python-urlgrabber |xargs rpm -e --nodeps# 下载yum与wget的rpm软件包 curl -O http://mirrors.aliyun.com/centos/7/os/x86_64/Packages/yum-3.4.3-168.el7.centos.noarch.rpm curl -O ht…...
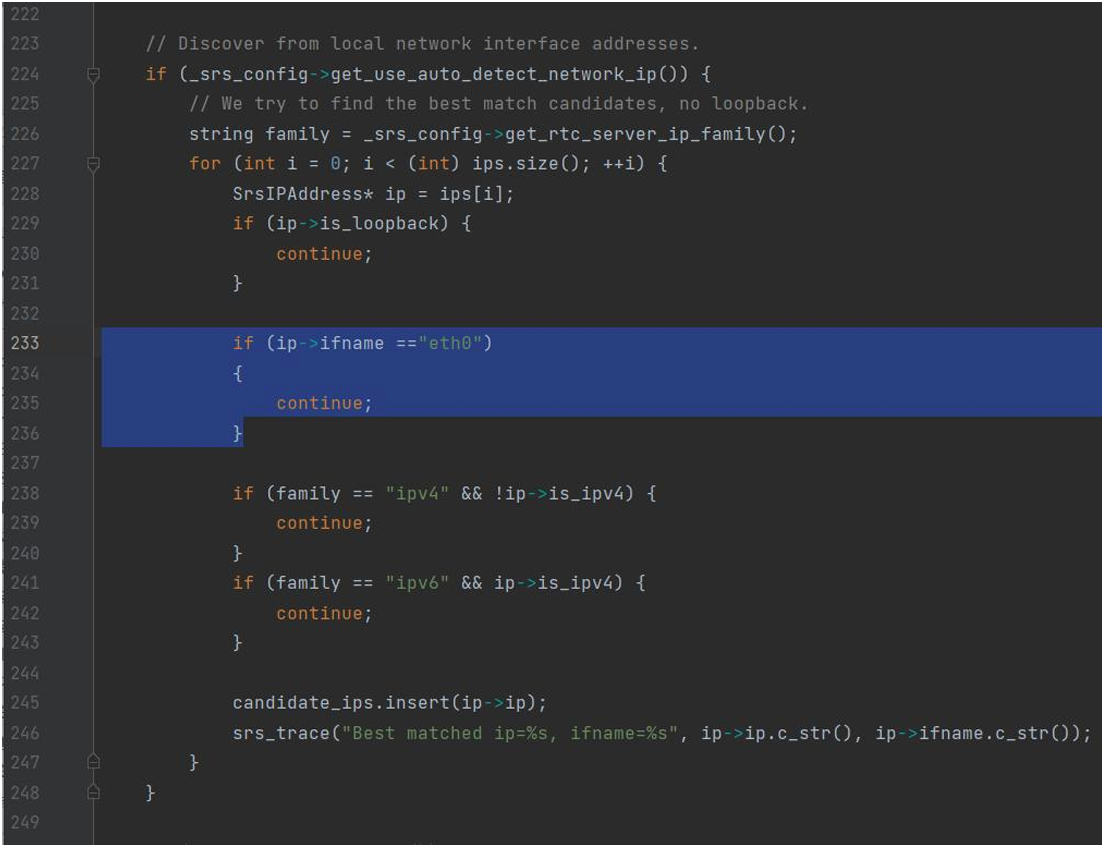
Ubuntu 编译SRS和ZLMediaKit用于视频推拉流
SRS实现视频的rtmp webrtc推流 ZLMediaKit编译生成MediaServer实现rtsp推流 SRS指定某个固定网卡,修改程序后重新编译 打开SRS-4.0.0/trunk/src/app/srs_app_rtc_server.cpp,在 232 行后面添加: ZLMediaKit编译后文件存放在ZLMediakit/rele…...

Intellij报错:the file size(3.47M) exceeds configured limit (2.56MB)
今天在部署一个教学平台的时候,当执行数据库脚本出现了以上问题。 自己把解决的方案分享给大家: 于IntelliJ IDEA或PyCharm,可以通过编辑idea.properties文件来增加文件大小限制。 打开idea.properties文件,通常位于IDE的安装目录…...

大数据技术全景解析:Spark、Hadoop、Hive与SQL的协作与实战
引言:当数据成为新时代的“石油” 在数字经济时代,数据量以每年50%的速度爆发式增长。如何高效存储、处理和分析PB级数据,成为企业竞争力的核心命题。本文将通过通俗类比场景化拆解,带你深入理解四大关键技术:Hadoop、…...

软考软件评测师——软件工程之系统维护
一、系统质量属性 可维护性 衡量软件系统适应修改的难易程度,包括修复缺陷、扩展功能或调整规模的效率。计算公式为:系统可用时间占比 1/(1平均修复时间),其中平均修复时间(MTTR)指排除故障所需的平均耗时。 可靠性 vs 可用性 可靠性&…...
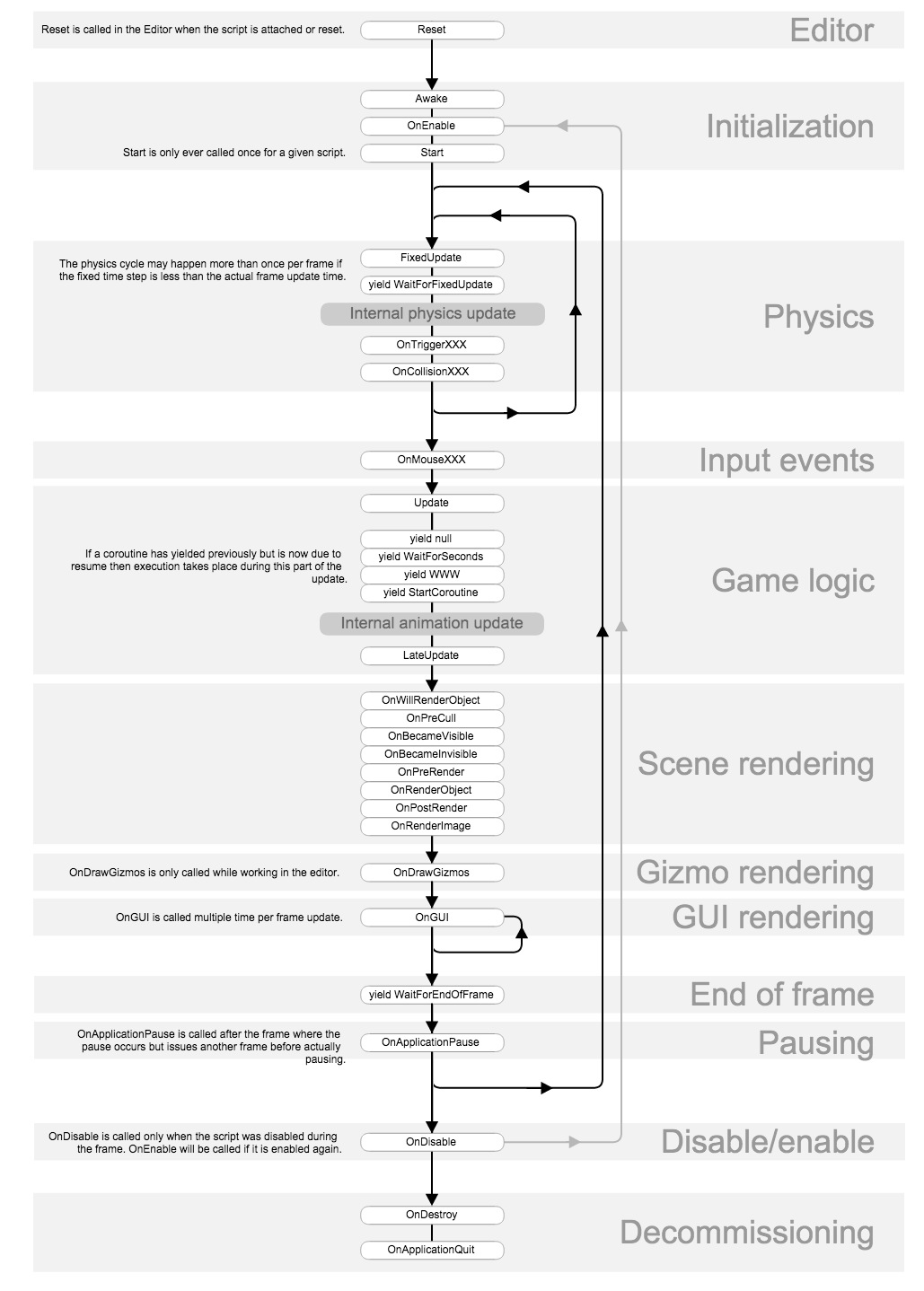
Unity动画与生命周期函数
一、Animator动画组件 Animator组件是Unity中用于管理和控制动画的主要工具,它可以处理复杂的动画状态机和动画片段之间的过 1.动画状态机 Animator组件的核心是动画状态机,它由多个动画状态和状态之间的过渡组成。可以通过Unity的动画窗口来创建和编辑…...

合并两个有序数组的高效算法详解
合并两个有序数组的高效算法详解 **合并两个有序数组的高效算法详解****1. 问题描述****2. 常见解法分析****方法 1:合并后排序(暴力法)****方法 2:双指针法(额外空间)** **3. 最优解法:双指针从…...
)
虚拟Python 环境构建器virtualenv安装(macOS版)
前提 之前我们使用pyenv安装好了Python 3.13.3,并且,全局都使用这个版本的python。现在我们来安装virtualenv。 pipx安装 brew install pipx pipx ensurepath sudo pipx ensurepath --global # optional to allow pipx actions with --global argumen…...

解决ubuntu20中tracker占用过多cpu,引起的风扇狂转
track是linux中的文件索引工具,ubuntu18之前是默认不安装的,所以在升级到20后会默认安装,它是和桌面程序gnome绑定的,甚至还有很多依赖项,导致无法删除,一旦删除很多依赖项都不能运行,禁用也很难…...

在线文档管理系统 spring boot➕vue|源码+数据库+部署教程
📌 一、项目简介 本系统采用Spring Boot Vue ElementUI技术栈,支持管理员和员工两类角色,涵盖文档上传、分类管理、公告发布、员工资料维护、部门岗位管理等核心功能。 系统目标是打造一个简洁高效的内部文档管理平台,便于员工…...
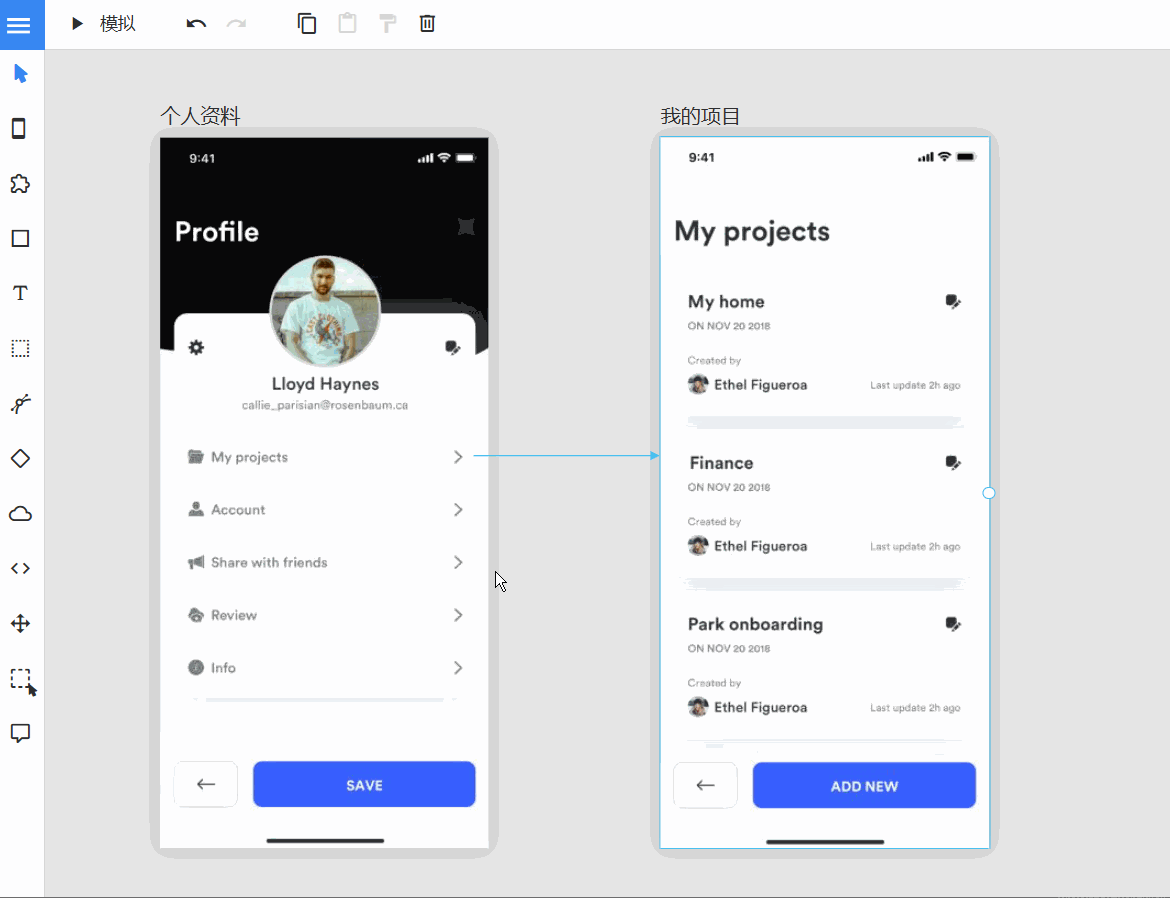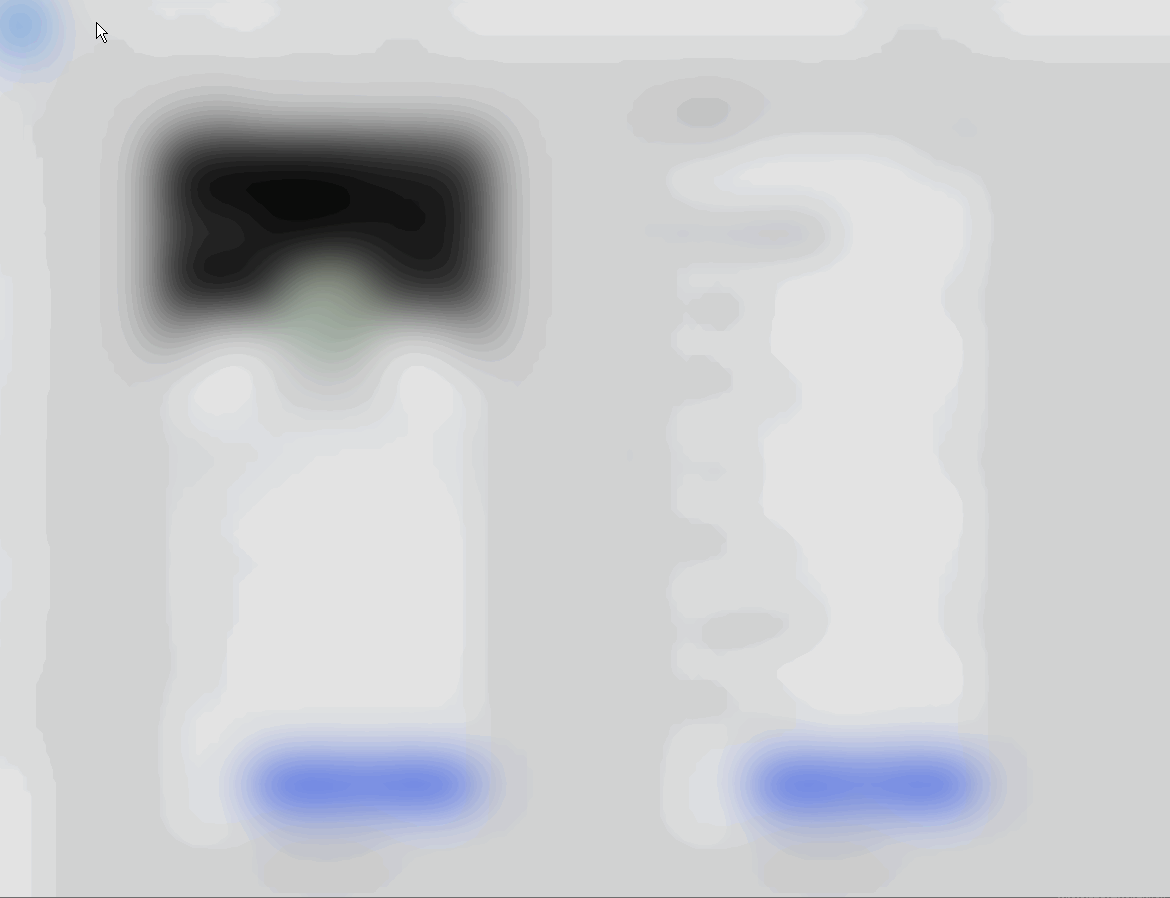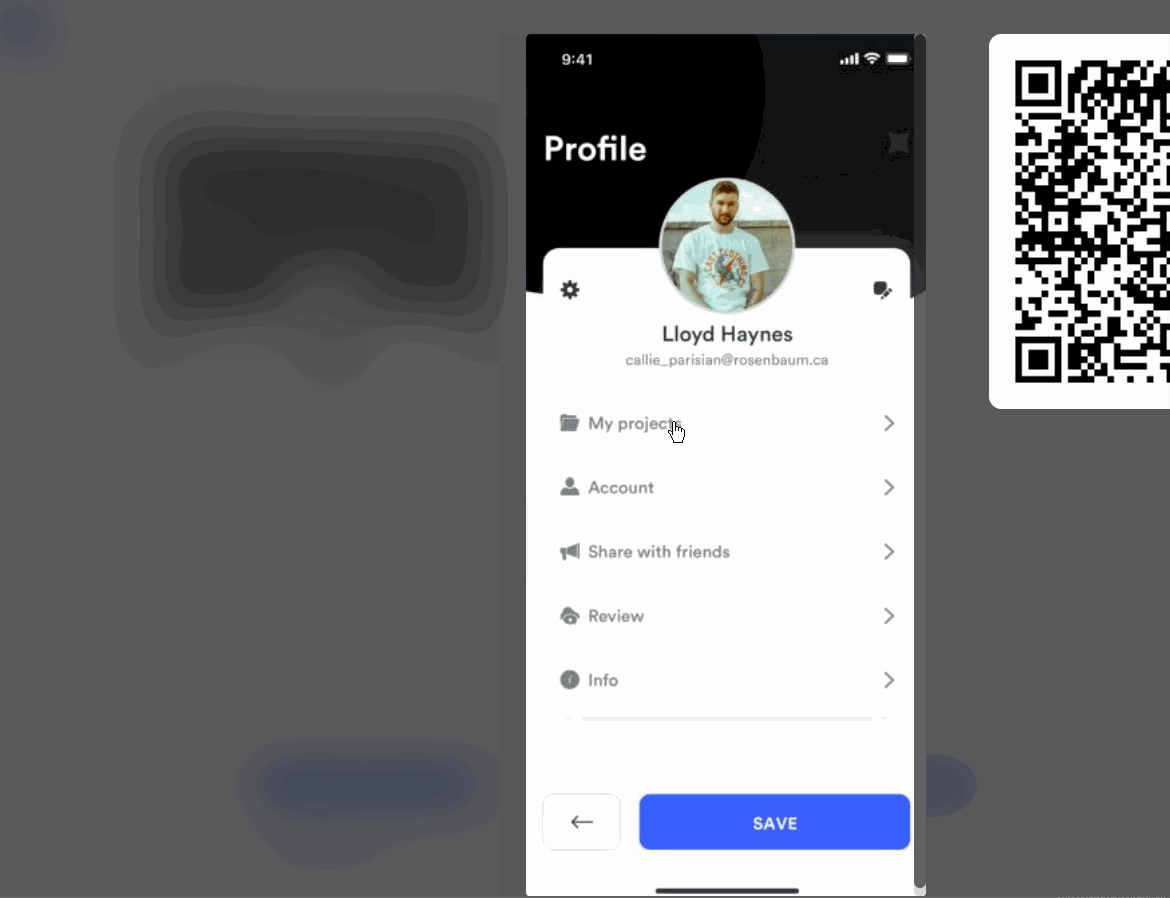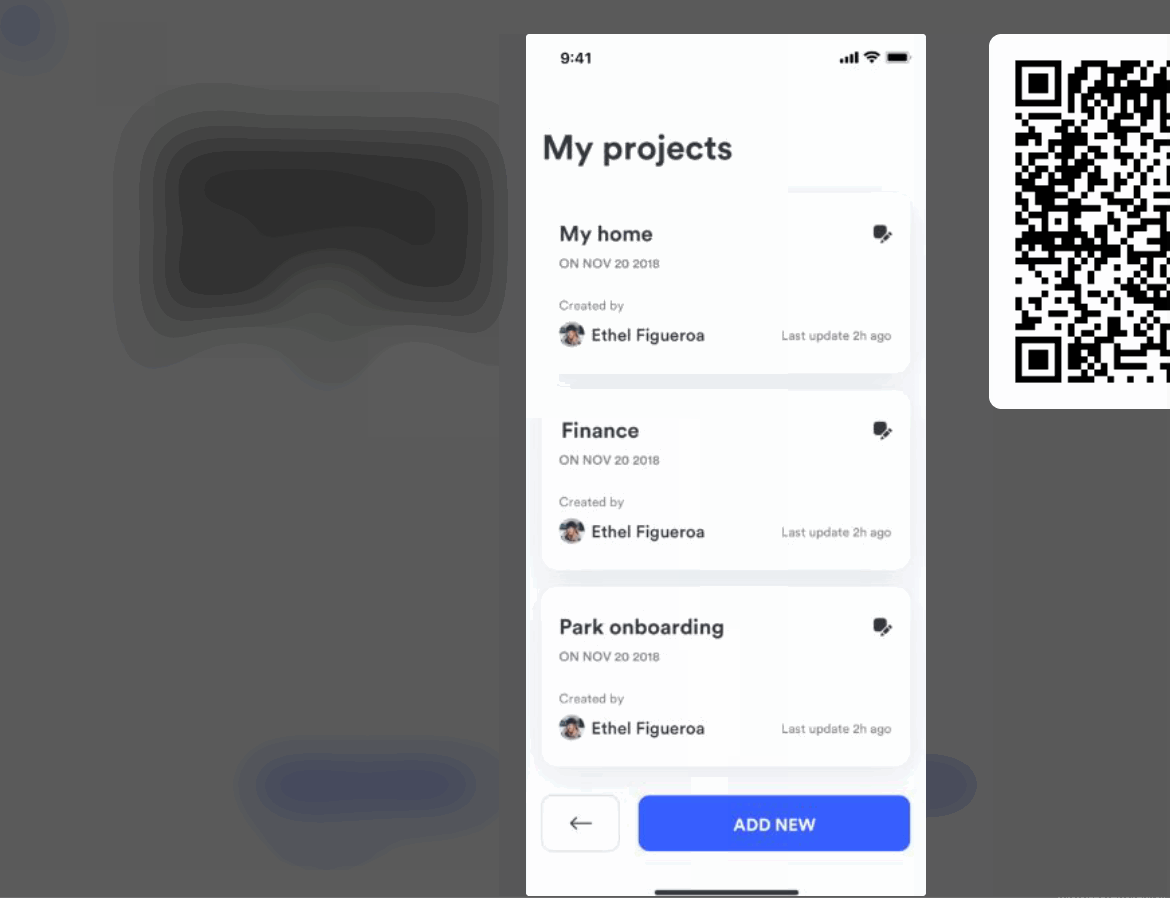
在UI 原型设计中,交互规则有哪些核心要素?
在UI 原型设计中,交互规则主要有三个核心要素,分别为重要性、原则与实践,具体表现在: 一、交互规则在 UI 原型设计中的重要性 明确交互逻辑:设计阶段制定交互规则,清晰定义界面元素操作响应。 如社交应用…...

CSS图片垂直居中问题解决方案
在 CSS 中,使用 vertical-align: middle 导致图片略微向下偏移的现象,本质上是由于 行内元素的基线对齐规则 和 父容器上下文环境 共同作用的结果。以下是具体原因和解决方案: 原因详解 1. vertical-align: middle 的真实含义 该属性 不会让…...

STC8H系列单片机STC8H_H头文件功能注释
#ifndef __STC8H_H__ // 条件编译:如果未定义__STC8H_H__宏 #define __STC8H_H__ // 则定义该宏,防止头文件被重复包含 / //包含本头文件后,不用另外再包含"REG51.H" // 提示:本头文件已包含基本寄存器定义 sfr P0 = …...

Python类的力量:第五篇:魔法方法与协议——让类拥有Python的“超能力”
文章目录 前言:从“普通对象”到“Python原生公民”的进化之路 一、魔法方法:赋予对象“超能力”的基因1. 构造与析构:对象生命周期的“魔法开关”2. 字符串表示:对象的“自我介绍”3. 运算符重载:让对象支持“数学魔法…...

OpenResty Manager 介绍与部署(Docker部署)
概述 OpenResty-Manager 是一个基于 OpenResty 构建的开源 Web 管理平台。OpenResty 是一个高性能的 Web 平台,集成了 Nginx 和 LuaJIT,支持强大的脚本功能。OpenResty-Manager 由 Safe3 开发,提供了一个用户友好的界面,用于管理…...

深入解析HTTP协议演进:从1.0到3.0的全面对比
HTTP协议作为互联网的基础协议,经历了多个版本的迭代演进。本文将详细解析HTTP 1.0、HTTP 1.1、HTTP/2和HTTP/3的核心特性与区别,帮助开发者深入理解网络协议的发展脉络。 一、HTTP 1.0:互联网的奠基者 核心特点: 短连接模式&am…...

快速搭建一个electron-vite项目
1. 初始化项目 在命令行中运行以下命令 npm create quick-start/electronlatest也可以通过附加命令行选项直接指定项目名称和你想要使用的模版。例如,要构建一个 Electron Vue 项目,运行: # npm 7,需要添加额外的 --: npm cre…...

【Android】Android 实现一个依赖注入的注解
Android 实现一个依赖注入的注解 🎯 目标功能 自定义注解 Inject创建一个 Injector 类,用来扫描并注入对象支持 Activity 或其他类中的字段注入 🧩 步骤一:定义注解 import java.lang.annotation.ElementType; import java.lan…...

unity terrain 在生成草,树,石头等地形障碍的时候,无法触发碰撞导致人物穿过模型
1.terrain地形的草,石头之类要选择模型预制体 2.在人物身上挂碰撞器和刚体,或者单挂一个character controller组件也行 3.在预制体上挂碰撞盒就好了,挂载meshcollider会导致碰撞无效...

使用gitbook 工具编写接口文档或博客
步骤一:在项目目录中初始化一个 GitBook 项目 mkdir mybook && cd mybook git init npm init -y步骤二:添加书籍结构(如 book.json, README.md) echo "# 我的书" > README.md echo "{}" > bo…...

75.xilinx复数乘法器IP核调试
(83*j)*(57j) 935j 正确的是 1971j 分析出现的原因:(abj)* (cdj) (ac-bd)j(adbc) 其中a,b,c,d都是16bit的有符号数,乘积的结果为保证不溢出需要32bit存储,最终的复数乘法结果是两个32b…...

软件工程之软件产品的环境
比较正规的做法是分下面的三个 1.开发环境(Development Environment): 用途:这是软件开发人员编写和测试代码的地方。在开发环境中,开发者可以自由地试验、调试代码,以及进行初步的功能实现和测试。 特点&…...

8.ADC
目录 ADC 模拟信号和数字信号的区别和区别 信号的区别 如何采集信号 常见的接口 数字接口 模拟接口 ADC 实际应用 ADC 转换器的定义 ADC 相关的名词 ADC 采集的原理 ADC 的参考电压 相关的计算 如何实现 ADC STM32 内的 ADC 转换器讲解 STM32 的 ADC 简介 AD…...

c/c++中程序内存区域的划分
c/c程序内存分配的几个区域: 1.栈区:在执行函数时,函数内局部变量的存储单元都可以在栈上创建,函数执行结束时这些存储单元自动被释放,栈内存分配运算内置于处理器的指令集中,效率很高但是分配的内存容量有…...

模糊综合评价模型建立
模糊综合评价模型建立 一、整体流程 二、代码实现(含大量注释) #程序文件ex14_4.py import numpy as npa np.loadtxt(data14_4.txt) # 使用定义匿名函数的形式来定义各个评价指标的隶属函数 f1 lambda x: x/8800 f2 lambda x: 1-x/8000 f3 lambda x: (x<5.5)(8-x)/(8-…...

【Linux】Linux安装mysql
该教程是使用的 CentOS 8.2 安装 mysql。 1.删除原有mysql rpm -qa|grep mariadb 如果存在在mariadb,卸载命令如下: #rpm -e --nodeps是强制卸载指令 后面是查出的依赖名称rpm -e --nodeps mariadb-libs-5.5.64-1.el7.x86_64全部卸载完输入以下指令&am…...

模仿学习笔记
模仿学习总共分两类: 行为克隆:BC,Dagger逆强化学习:又分为 2.1基于最大边际逆强化学习 (无法主要歧义问题):学徒学习 2.2 基于最大熵逆强化学习 (主要解决歧义问题):GAIL 学徒学习 基于最大熵…...

一文讲透 Vue3 + Three.js 材质属性之皮革篇【扫盲篇】
文章目录 前言一、Three.js材质系统基础1.1 为什么选择PBR材质?1.2 关键参数解析 二、不同类型皮革的材质配置2.1 牛皮材质实现2.2 羊皮材质实现2.3 仿皮材质实现 三、高级贴图技术3.1 贴图制作流程3.2 组合贴图实战 四、性能优化策略4.1 贴图压缩技术4.2 材质共享4…...
