WebGL图形编程实战【7】:变换流水线 × 坐标系与矩阵精讲
变换流水线
- 局部坐标系:是坐标系以物体的中心为坐标原点,物体的旋转、平移等操作都是围绕局部坐标系进行的,这时,当物体模型进行旋转或平移等操作时,局部坐标系也执行相应的旋转或平移操作。
- 世界坐标系:一个三维场景中通常都不会只有一个物体.我们真正需要的是把我们建立的物体按照我们所需要的形式摆放在场景之中.每个物体分布在场景的适当的位置上.整个场景的坐标系就称为世界坐标系
- 相机坐标系:相机的重心为原点,上方向为y轴,原点与视点的连线为z轴,x轴为yoz面的垂线
- 投影坐标系:是相机坐标系经过投影矩阵转换后得到的空间坐标系,之所以叫裁剪坐标系,是因为投影矩阵约定了视角的上下左右前后边界(对应的是相机的Frustum范围),后面会将处于边界之外的数据直接Clip到边界上
- 规范化设备坐标系(Normalized Device Coordinates):NDC指的是与设备平台无关的一套三维坐标系(比如同一个物件,无论设备使用什么样的分辨率,在这个坐标系中的数值都是相同的)
- 屏幕坐标系:是NDC坐标系经过视口变换后得到的空间坐标系,即NDC坐标系在屏幕上所占的比例,即屏幕坐标系
模型变换
模型变换:是从模型坐标系到世界坐标系的转换。
简单通俗来讲,3D建模之初,模型有自己的坐标系,以及相应的点坐标。就是将场景中的模型摆好,这个过程就叫模型变换。
在复合变化当中,模型变换不同顺序有不同的结果,其实就是因为矩阵相乘不满足交换律,但满足结合律,所以对应同一个复合变换,可以先得出其中的基础变换的矩阵乘积,再与输入向量相乘。
齐次坐标
在欧式几何当中,最重要的一个定理是:两条平行线永不相交。但是在实际生活应用中有很多非欧式几何的场景,比如:透视空间、透视投影等。那么齐次坐标就是用来解决这个问题的。
概述
齐次坐标是用n+1维向量表示n维向量的坐标系统,用于统一几何变换和表示无穷远点
-
定义与基本概念
齐次坐标是一种数学工具,通过增加一个额外维度将n维向量表示为n+1维向量。例如:- 二维点(x,y)的齐次坐标为(x,y,w),其中w为非零实数,实际坐标可通过(x/w, y/w)还原。
- 三维点(x,y,z)同理扩展为(x,y,z,w)。
- 核心特点:齐次坐标具有规模不变性,即(kx,ky,kw)(k!=O)与原坐标(x,y,w)表示同一个点。
-
引入齐次坐标的目的
- 统一几何变换:在计算机图形学中,平移、旋转、缩放等变换可通过单一的4x4矩阵乘法完成,简化计算。
- 表示无穷远点:当w=0时,(x,y,0)表示二维空间中的无穷远点(方向向量),解决了欧氏坐标无法表达无限远的问题。
- 射影几何兼容:平行线在射影空间中相交于无穷远点,齐次坐标为此提供了代数支持。
-
规范化处理
- 齐次坐标的规范化指将W置为1(即(x,y,w)→ (x/w,y/w,1)),以消除尺度不确定性,便于实际计算。
-
数学原理示例
- 平行线相交证明:
在齐次坐标系下,两条平行线Ax+By+C=O和Ax+By+D=O可表示为Ax+By+Cw=O和Ax+By+Dw=0。当w=O时,解为(B,-A,0),即无穷远交点。
- 平行线相交证明:
优势
- 可以表示无穷远
- 可以表示点在直线或者平面
在齐次坐标下,判断点是否位于直线或平面上的条件可统一表示为向量内积为零
二维空间中点在直线上的判断
- 直线表示:直线方程为 ax + by + c = 0 ,用齐次坐标表示为向量 l = (a, b, c) ^ T。
- 点的齐次坐标:点 P = (x, y) 的齐次坐标为 P’ = (x, y, 1)。
- 判定条件:点 P 在直线 l 上的充要条件是内积 l x P’ = 0 ,即:
ax + by + c*1 = 0 <=> ax + by + c = 0 - 几何意义:内积为零等价于点坐标满足直线方程。
三维空间中点在平面上的判断
- 平面表示:平面方程为 ax + by + cz + d = 0 ,用齐次坐标表示为向量 s = (a, b, c, d)^T 。
- 点的齐次坐标:点 P = (x, y, z) 的齐次坐标为 P’ = (x, y, z, 1) 。
- 判定条件:点 P 在平面 s 上的充要条件是内积 s * P’ = 0 ,即:
ax + by + cz + d * 1 = 0 <=> ax + by + cz + d = 0 - 几何意义:内积为零等价于点坐标满足平面方程。
总结
- 核心条件:点 P 的齐次坐标 P’ 与直线 l 或平面 s 的内积为零。
- 优势:统一处理有限点和无穷远点,不依赖坐标缩放,简化几何计算。
- 公式表示:
- 二维直线:l * P’ = 0 其中 P’ = (x, y, 1)
- 三维平面:s * P’ = 0 其中 P’ = (x, y, z, 1)
- 可以表示两条直线的交点
在齐次坐标下,两条直线 l 和 m 的交点可以通过叉乘运算直接计算,并利用点积条件验证其几何意义
直线交点的齐次坐标表示
- 叉乘定义:在二维投影几何中,两条直线 l = (a1, b1, c1)^T 和 m = (a2, b2, c2)^T 的交点 ( \mathbf{p} ) 由叉乘给出:
p = l * m
叉乘结果 p = (px, py, pw)^T 是一个齐次坐标点。
交点满足两条直线的方程
- 点积条件:若 p 是两直线的交点,则它必须同时位于 l 和 m 上。根据点在直线上的条件(l ^ T * p = 0) 和(m ^ T * p = 0),可以验证:
l ^T * p = l ^ T (l * m) = 0
m ^T * p = m ^ T (l * m) = 0
几何意义:叉乘结果 p 与 l 和 m 正交,因此满足直线方程。
叉乘的几何解释
- 正交性:叉乘l * m 生成的向量 p 与 l 和 m 均正交。在齐次坐标下,这等价于点 p 同时位于两直线上。
- 交点的唯一性:在投影平面中,两条不平行的直线必有唯一交点,叉乘直接给出了这一交点的齐次坐标。
齐次坐标的归一化
- 坐标形式:叉乘结果 p = (px, py, pw)^T 可能为齐次坐标,需归一化得到欧氏坐标:
欧氏坐标 = ( p_x/p_w, p_y/p_w) (若 p_w != 0).
- 无穷远点:若 p_w = 0,则 p 表示无穷远点,说明两直线在欧氏空间中平行。
- 能够区分一个向量和一个点
点和向量的区别
- 点:表示空间中的一个具体位置,例如三维点(x,y,z)
- 向量:表示方向和大小,没有位置属性,例如位移向量(dx,dy,dz)
普通坐标 → 齐次坐标
-
点的转换:普通坐标点 (x, y, z) 转换为齐次坐标时,添加第四个分量 1:
齐次坐标点:} \quad (x, y, z, 1).
-
向量的转换:普通坐标向量 (x, y, z) 转换为齐次坐标时,添加第四个分量 0:
齐次坐标向量:(x, y, z, 0).
齐次坐标 → 普通坐标
-
点的还原:若齐次坐标为 (x, y, z, 1),直接去掉第四个分量 1,还原为普通坐标点:
普通坐标点:(x, y, z)
-
向量的还原:若齐次坐标为 ((x, y, z, 0)),去掉第四个分量 0,还原为普通坐标向量:
普通坐标向量:(x, y, z)
不同方式的图形变换
平移
让x的坐标+2表示沿着x平移
- 手动变换
const data = new Float32Array([1.0, 0.0, 0.0, 1.0,0.0, 1.0, 0.0, 1.0,0.0, 0.0, 1.0, 1.0,
])const data = new Float32Array([3.0, 0.0, 0.0, 1.0,2.0, 1.0, 0.0, 1.0,2.0, 0.0, 1.0, 1.0,
])
- js变换(CPU)
for (let i = 0; i < data.length; i += 4) {data[i] += 2.0;
}
- 着色器(GPU)
gl_Position = vec4(apos.x + 2.0, apos.y, apos.z, 1);
- 平移矩阵

旋转
- 手动变换
const newArray = new Float32Array([1.0, 0.0, 0.0, 1.0,1.0, 1.0, 0.0, 1.0,1.0, 0.0, 1.0, 1.0
]);const newArray = new Float32Array([1.0, 0.0, 0.0, 1.0,1.0, 1.0, 0.0, 1.0,1.0, 0.0, 1.0, 1.0
]);
- js变换(CPU)
const newArray = new Float32Array(data.length);
const angle = Math.PI / 2;
for (let i = 0; i < data.length; i += 4) {newArray[i] = data[i] * Math.cos(angle) - data[i + 1] * Math.sin(angle);newArray[i + 1] = data[i] * Math.sin(angle) + data[i + 1] * Math.cos(angle);newArray[i + 2] = data[i + 2];newArray[i + 3] = data[i + 3];
}
- 着色器(GPU)
gl_Position = vec4(apos.x * cosb - apos.y * sinb, apos.x * sinb + apos.y * cosb, apos.z, 1);
- 旋转矩阵

缩放
- 手动变换
const newArray = new Float32Array([1.0, 0.0, 0.0, 1.0,1.0, 1.0, 0.0, 1.0,1.0, 0.0, 1.0, 1.0
]);const newArray = new Float32Array([2.0, 0.0, 0.0, 1.0,2.0, 1.0, 0.0, 1.0,2.0, 0.0, 1.0, 1.0
]);
- js变换(CPU)
const newArray = new Float32Array(data.length);
for (let i = 0; i < data.length; i += 4) {newArray[i] = data[i] * 2;newArray[i + 1] = data[i + 1] * 2;newArray[i + 2] = data[i + 2] * 2;newArray[i + 3] = data[i + 3];
}
- 着色器(GPU)
gl_Position = vec4(apos.x * 2, apos.y * 2, apos.z * 2, 1);
- 缩放矩阵

视图变换
进入世界坐标系空间之后,物体与WebGL相机虽然建立了联系,但是并没有进一步确定观察物体的状态。当我们把相机的位置进行移动的时候,相机坐标系和世界坐标系不再重合。这意味着我们直接将世界坐标作为最终的坐标绘制,并不能正确的描述观察者和物体之间的位置关系。如图,我们将相机沿着x 轴正方向移动 1 个单位。此时世界坐标系的原点(0,0,0)在相机坐标系中的坐标就变成(-1,0,0),这说明我们需要在两个坐标系之间进行转换!这个时候就需要调整相机位置姿态,也就是视图变换。
公式推导
可以看这个知乎的文章:视图变换和投影变换矩阵的原理及推导,以及OpenGL,DirectX和Unity的对应矩阵
在相机坐标系当中,分别用d(向前向量 direction), u(向上向量 up ), r(向右向量right)和p(位置 position)来表示这四个变量。
并假设待求的视图矩阵为V(将摄像机移动到原点),并将摄像机的三个向量分别与坐标轴对齐,d与z轴正方向对齐,u与y轴正方向对齐,r与x轴正方向对齐。假设将摄像机与坐标轴对齐的矩阵为V,那么V的推导过程如下
其中d、u、r通常这些向量是正交的,且满足右手坐标系的关系
r = u × d , u = d × r , d = r × u
- 平移矩阵T:
- 将相机的位置p移到原点
- 旋转矩阵R:
- 将相机的三个正交单位向量r(右)、u(上)、d(前)旋转到与坐标轴对齐。旋转矩阵由这三个向量作为行向量构成
- 组合视图矩阵V:
- 先应用平移,再应用旋转,因此矩阵相乘顺序为R * T

视图变换案例
通过一个透视投影矩阵,模拟人眼观察效果(FOV 视野角度)
glMatrix.mat4.perspective(projMatrix, 30.0, canvas.width / canvas.height, 1.0, 100.0);
初始化相机矩阵(视图矩阵)使用 lookAt 函数创建视图矩阵,表示相机的位置、目标点和上方向
参数说明:修改 x, y, z 值会改变相机的目标点,从而调整视角
- [3.0, 3.0, 3.0]: 相机的初始位置(位于 (3, 3, 3) 点)
- [x, y, z]: 目标点,即相机看向的方向(由 setTranslate 的参数决定)
- [0.0, 1.0, 0.0]:上方向向量(Y轴向上)
const viewMatrix = glMatrix.mat4.create();
glMatrix.mat4.lookAt(viewMatrix, [3.0, 3.0, 3.0], [x, y, z], [0.0, 1.0, 0.0]);
创建模型矩阵并计算 MVP 矩阵:
模型矩阵 (modelMatrix) 表示物体本身的变换(如平移、旋转等)
- MVP 矩阵是通过将投影矩阵 (projMatrix)、视图矩阵 (viewMatrix) 和模型矩阵 (modelMatrix) 相乘得到的
- 最终的 MVP 矩阵传递给着色器中的 u_formMatrix,用于顶点坐标变换
let modelMatrix = glMatrix.mat4.create();
u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_formMatrix');
MVPMatrix = glMatrix.mat4.create();
glMatrix.mat4.multiply(MVPMatrix, projMatrix, glMatrix.mat4.multiply(MVPMatrix, viewMatrix, modelMatrix));
gl.uniformMatrix4fv(u_ModelMatrix, false, MVPMatrix);
第一人称视角
第一人称视角的核心是相机始终位于观察者的“眼睛”位置,并朝向观察方向
视线方向与水平方向计算
- lookAtDirction: 从相机位置指向目标点的方向向量(即视线方向)
- rightDirection: 水平方向向量,通过视线方向与上方向叉乘得到
const lookAtDirction = glMatrix.vec3.subtract(glMatrix.vec3.create(), lookAtPosition, eyePosition);
glMatrix.vec3.normalize(lookAtDirction, lookAtDirction);const rightDirection = glMatrix.vec3.cross(glMatrix.vec3.create(), updirction, lookAtDirction);
glMatrix.vec3.normalize(rightDirection, rightDirection);
第三人称视角
与第一人称视角不同的是,相机始终位于观察对象的后方或侧面,用户可以看到自己控制的角色或物体
| 特性 | 第一人称视角 | 第三人称视角 |
|---|---|---|
| 相机位置 | 位于“眼睛”位置,跟随移动 | 固定在角色背后或侧面,不随移动变化 |
| 目标点 | 始终指向视线前方 | 始终指向角色中心 |
| 移动方式 | 相机位置改变,视角跟随移动 | 角色移动,相机视角固定或绕其旋转 |
| 交互操作 | 按钮控制前后左右移动 | 按钮控制视角绕角色旋转 |
| 视觉体验 | 用户感觉自己在场景中行走 | 用户看到角色在场景中活动 |
投影变换
在前面已经了解了正交投影和透视投影,WebGL图形编程实战【3】:矩阵操控 × 从二维到三维的跨越
公式推导
正交投影

正交投影可以分为两步:第一步为平移,第二步为缩放。将长方体(目标)投影到画布上

透视投影

案例
在进行正交投影和透视投影的时候可以直接使用封装好的函数
glMatrix.mat4.ortho(projMatrix, -1, 1, -1, 1, -1, 100);
glMatrix.mat4.perspective(projMatrix, 30.0, canvas.width / canvas.height, 1.0, 100.0);
还是以正方体展示为例:
NDC变换

视口变换
该转换的目的在于将某个在ndc坐标系的点p(x, y, z) ,转换为屏幕坐标系中的点p1(x1, y1, z1) , 更具体的来说 就是将x轴的 [-1,1]转换为[X,X + Width],将y轴的[-1,1]转换为[Y,Y + Height], 将z轴的[-1,1] 转换为[near,far]

相关文章:

WebGL图形编程实战【7】:变换流水线 × 坐标系与矩阵精讲
变换流水线 #mermaid-svg-Omabd9LSNCdIvWqB {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-Omabd9LSNCdIvWqB .error-icon{fill:#552222;}#mermaid-svg-Omabd9LSNCdIvWqB .error-text{fill:#552222;stroke:#552222;…...

在Angular中使用Leaflet构建地图应用
Leaflet是一个用于创建地图的JavaScript库,它包含许多功能,并且非常适用于移动设备。 准备 nodejs: v20.15.0 npm: 10.7.0 angular: 19.2.10 创建一个地图应用工程 npx angular/cli new my-leaflet-app --stylecss --routingfalse --skip-tests提示 …...

鸿蒙next播放B站视频横屏后的问题
(此文讨论范围为b站视频链接,且不包括b站直播链接;android/iOS的webview播放b站视频完全没有这么多问题) 1、竖屏播放没问题 从一个竖屏页p1点击进入视频页p2,p2页仍为竖屏; p2页有一Web组件,…...

DVWA靶场通关笔记-SQL注入(SQL Injection Medium级别)
目录 一、SQL Injection 二、代码审计(Medium级别) 1、源码分析 (1)index.php (2)Medium.php 2、渗透思路 (1)SQL安全问题分析 (2)SQL渗透思路 三、…...

vue异步导入
vue的异步导入 大家开发vue的时候或多或少路由的异步导入 component: () >import(“/views/A_centerControl/intelligent-control/access-user-group”),当然这是路由页面,那么组件也是可以异步导入的 使用方式 组件的异步导入非常简单,主要是一个…...

【Redis】压缩列表
目录 1、背景2、压缩列表【1】底层结构【2】特性【3】优缺点 1、背景 ziplist(压缩列表)是redis中一种特殊编码的双向链表数据结构,主要用于存储小型列表和哈希表。它通过紧凑的内存布局和特殊的编码方式来节省内存空间。 2、压缩列表 【1…...

2025年,如何制作并部署一个完整的个人博客网站
欢迎访问我的个人博客网站:欢迎来到Turnin的个人博客 github开源地址:https://github.com/Re-restart/my_website 前言 2024年年初,从dji实习回来之后,我一直想着拓宽自己的知识边界。在那里我发现虽然大家不用java,…...

.NET 8 + Angular WebSocket 高并发性能优化
.NET 8 Angular WebSocket 高并发性能优化。 .NET 8 WebSocket 高并发性能优化 WebSocket 是一种全双工通信协议,允许客户端和服务端之间保持持久连接。在高并发场景下,优化 WebSocket 的性能至关重要。以下是针对 .NET 8 中 WebSocket 高并发性能优化…...

腾讯云运营开发 golang一面
redis为什么单线程会快 每秒10w吞吐量 io多路复用 一个文件描述符整体拷贝;调用epoll_ctl 单个传递 内核遍历文件描述符判断是否有事件发送;回调函数列表维护 修改有事件发送的socket为可读或可写,返回整个文件描述符;返回链…...

一个简单的静态页面
这个页面采用了现代化的 UI 设计,包括卡片式布局、微交互动画、分层设计和响应式结构。页面结构清晰,包含导航栏、英雄区域、功能介绍、产品特性、用户评价和联系表单等完整组件,可作为企业官网或产品介绍页面的基础模板。 登录后复制 <!D…...

使用 163 邮箱实现 Spring Boot 邮箱验证码登录
使用 163 邮箱实现 Spring Boot 邮箱验证码登录 本文将详细介绍如何使用网易 163 邮箱作为 SMTP 邮件服务器,实现 Spring Boot 项目中的邮件验证码发送功能,并解决常见配置报错问题。 一、为什么需要邮箱授权码? 出于安全考虑,大…...

多模态大语言模型arxiv论文略读(六十八)
Image-of-Thought Prompting for Visual Reasoning Refinement in Multimodal Large Language Models ➡️ 论文标题:Image-of-Thought Prompting for Visual Reasoning Refinement in Multimodal Large Language Models ➡️ 论文作者:Qiji Zhou, Ruoc…...

APS「多目标平衡算法」如何破解效率与弹性的永恒博弈
APS(高级计划与排程)系统作为企业智能制造的核心引擎,通过整合需求预测、产能规划、生产调度、物料管理及数据分析等模块,构建了覆盖产品全生产流程的“感知-决策-执行-优化”闭环体系。 精准需求预测 APS系统通过构建需求特征数…...

网张实验操作-防火墙+NAT
实验目的 了解防火墙(ENSP中的USG5500)域间转发策略配置、NAT(与路由器NAT配置命令不同)配置。 网络拓扑 两个防火墙连接分别连接一个内网,中间通过路由器连接。配置NAT之后,内网PC可以ping公网…...
)
Spring 中常见的属性注入方式(XML配置文件)
在 Spring 中,XML 配置属性注入。 以下是几种常见的属性注入方式及其对应的简单示例代码。 1. 构造器注入 构造器注入是指通过类的构造函数来设置依赖项。 示例类: public class MyService {private final MyRepository myRepository;public MyService(MyRepository myRe…...

让 - 艾里克・德布尔与斯普林格出版公司:科技变革下的出版业探索
在数字化浪潮席卷全球的当下,传统出版行业面临着前所未有的挑战与机遇。《对话 CTO,驾驭高科技浪潮》的第 10 章聚焦于让 - 艾里克・德布尔(Jean - Eric Debeure)及其所在的斯普林格出版公司(Springer Publishing Comp…...

【技巧】离线安装docker镜像的方法
回到目录 【技巧】离线安装docker镜像的方法 0. 为什么需要离线安装? 第一、 由于docker hub被墙,所以 拉取镜像需要配置国内镜像源 第二、有一些特殊行业服务器无法接入互联网,需要手工安装镜像 1. 可以正常拉取镜像服务器操作 服务器…...

05 web 自动化之 selenium 下拉鼠标键盘文件上传
文章目录 一、下拉框操作二、键盘操作三、鼠标操作四、日期控件五、滚动条操作六、文件上传七、定位windows窗口及窗口的元素总结:页面及元素常用操作 一、下拉框操作 from selenium.webdriver.support.select import Select import time from selenium.webdriver.…...

《Python星球日记》 第73天:情感分析与主题建模
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、情感分析基础1. 情感分析的应用场景2. 基于规则的方法3. 基于深度学习的方法3.1 使用LSTM进行情感分析3.2 基于BERT的情感分析二、主题建模…...

数学复习笔记 10
前言 我觉得数学的高分乃至满分属于那些,聪明,坚韧,勇敢,细致的人。我非常惭愧自己不是这样的人,我在生活中发现了这样的同学,和他们交流的时候我常常感到汗流浃背,因为他们非常扎实的基础知识…...

07 web 自动化之 Unittest 应用:测试报告装饰器断言
文章目录 一、常见的第三方库结合 unittest 生产 html 格式测试报告1、HtmlTestRunner2、BeatifulReport 二、装饰器 unittest.skip 强制跳过&条件跳过三、unittest的常用断言方法 一、常见的第三方库结合 unittest 生产 html 格式测试报告 1、HtmlTestRunner 官网下载 …...

Spring Cloud探索之旅:从零搭建微服务雏形 (Eureka, LoadBalancer 与 OpenFeign实战)
引言 大家好!近期,我踏上了一段深入学习Spring Cloud构建微服务应用的旅程。我从项目初始化开始,逐步搭建了一个具备服务注册与发现、客户端负载均衡以及声明式服务调用功能的基础微服务系统。本文旨在记录这一阶段的核心学习内容与实践成果…...

9.2.高并发系统
目录 一、高并发系统设计原则 核心设计哲学 • CAP权衡:一致性、可用性、分区容错性的场景化选择 • BASE理论:最终一致性与柔性事务的落地策略 性能与扩展性准则 • 水平扩展 vs 垂直扩展:无状态服务与有状态服务的扩展策略 • 异步化设计…...
之planning_base)
Apollo学习——planning模块(3)之planning_base
planning_component、planning_base、on_lane_planning 和 navi_planning 的关系 1. 模块关系总览 继承层次 PlanningComponent:Cyber RT 框架中的 入口组件,负责调度规划模块的输入输出和管理生命周期。PlanningBase:规划算法的 抽象基类&…...

当 AI 邂逅丝路:揭秘「丝路智旅」,用 RAG 重塑中阿文化旅游体验
目录 系统命名:丝路智旅 (Silk Road Intelligent Travel)系统概述系统架构设计系统功能模块技术选型:为何是它们?系统优势与特点未来展望与扩展总结在数字浪潮席卷全球的今天,古老的丝绸之路正在以一种全新的方式焕发生机。当深厚的文化底蕴遇上尖端的人工智能技术,会碰撞…...

18.Excel数据透视表:第1部分创建数据透视表
一 什么是数据透视表 通过万花筒可以用不同的方式査看里面画面图像,在excel中可以将数据透视表看作是对准数据的万花筒,用不同角度去观察数据,也可以旋转数据,对数据进行重新排列,对大量的数据可以快速的汇总和建立交叉…...
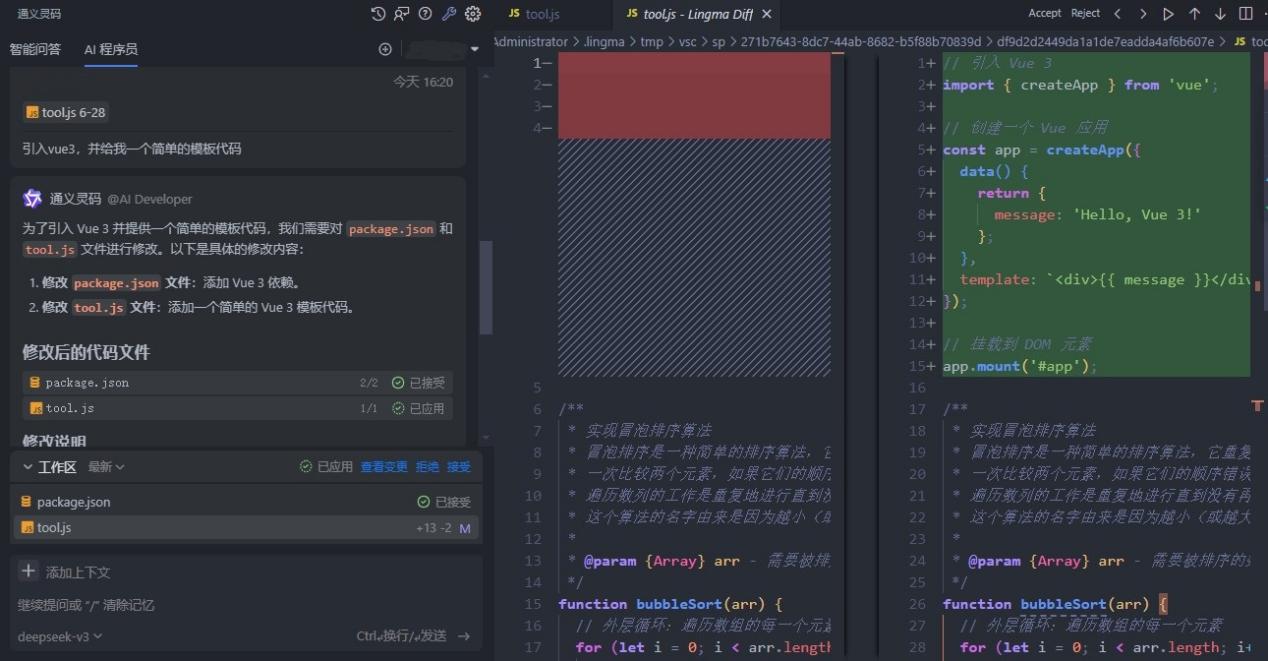
CSS AI 通义灵码 VSCode插件安装与功能详解
简介 在前端开发领域,页面调试一直是个繁琐的过程,而传统开发中美工与前端的对接也常常出现问题。如今,阿里云技术团队推出的通义灵码智能编码助手,为前端开发者带来了新的解决方案,让开发者可以像指挥者一样…...
)
每日c/c++题 备战蓝桥杯(P1002 [NOIP 2002 普及组] 过河卒)
洛谷P1002 [NOIP 2002 普及组] 过河卒 题解 题目描述 过河卒是一道经典的动态规划题目。题目大意是:一个卒子从棋盘左上角(0,0)出发,要走到右下角(n,m),棋盘上有一个马在(x,y)位置,卒子不能经过马所在位置及其周围8个位置。求卒…...
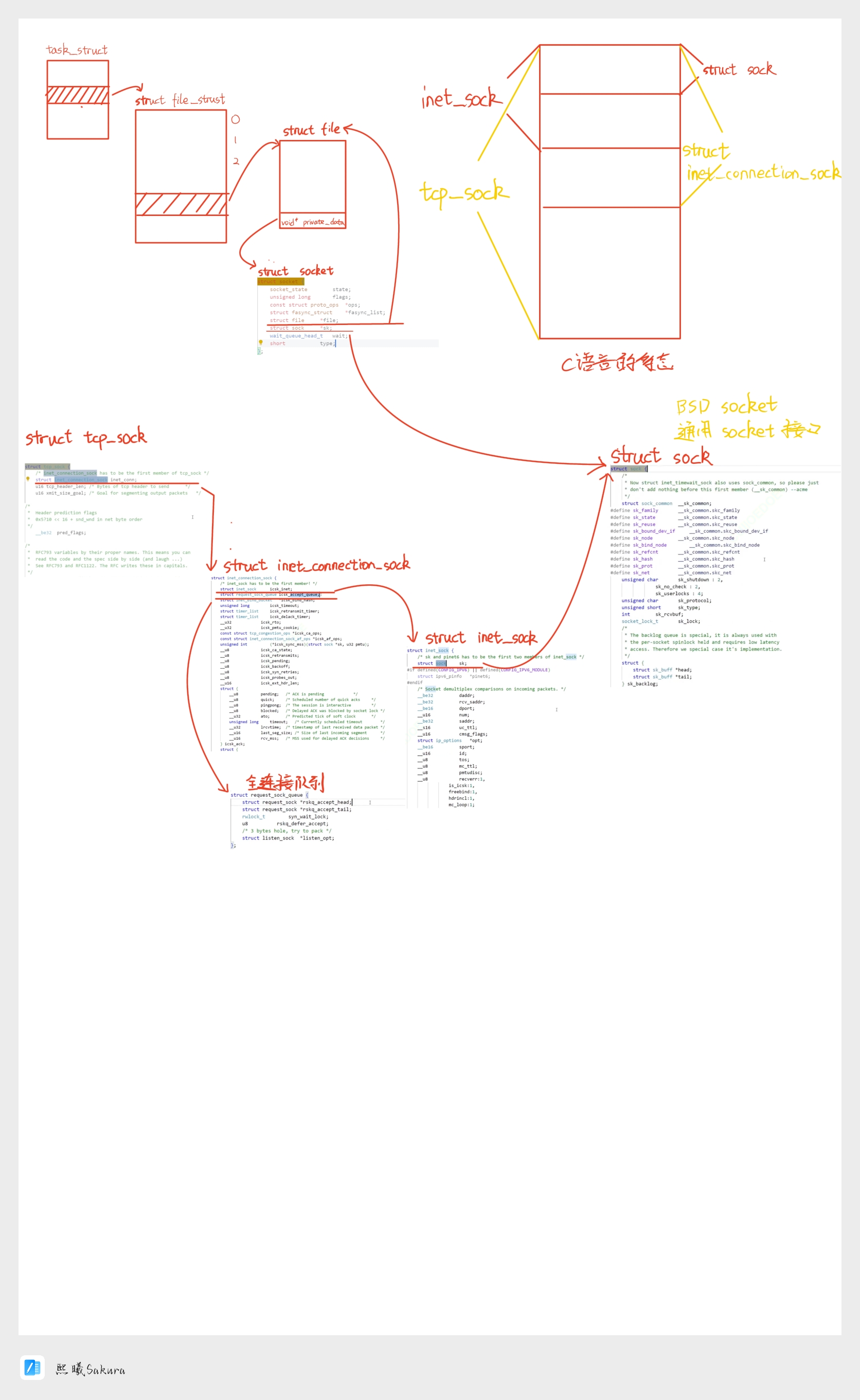
【Linux网络】TCP全连接队列
TCP 相关实验 理解 listen 的第二个参数 基于刚才封装的 TcpSocket 实现以下测试代码对于服务器, listen 的第二个参数设置为 1, 并且不调用 accept测试代码链接 test_server.cc #include "tcp_socket.hpp"int main(int argc, char* argv[]) {if (argc ! 3) {pri…...
HTML 颜色全解析:从命名规则到 RGBA/HSL 值,附透明度设置与场景应用指南
一、HTML 颜色系统详解 HTML 中的颜色可以通过多种方式定义,包括颜色名称、RGB 值、十六进制值、HSL 值等,同时支持透明度调整。以下是详细分类及应用场景: 1. 颜色名称(预定义关键字) HTML 预定义了 140 个标准颜色名…...
