【C++】 —— 笔试刷题day_29
一、排序子序列
题目解析

一个数组的连续子序列,如果这个子序列是非递增或者非递减的;这个连续的子序列就是排序子序列。
现在给定一个数组,然后然我们判断这个子序列可以划分成多少个排序子序列。
例如:
1 2 3 2 2 1可以划分成1 2 3和2 2 1两个排序子序列
算法思路
对于这道题,思路就很简单了:
暴力解法
从
0位置开始遍历,寻找一段连续子序列,直到这一段子序列不满足排序子序列的条件,即找到了一个排序子序列;然后继续从上次遍历结束位置接着遍历数组,寻找下一个子序列。
贪心优化:
当我们遍历到数组中数值相同的区域时,我们要知道,要找的子序列是非递增或者非递减的;
所以这一段相等的序列,我们可以加到前面或者后面的任意序列中。
所以我们在遇到数值相等的子序列时,继续向后遍历即可。
但是这样我们会发现两个问题:
- 如果数组刚开始位置的数据是相等的,我们不知道这段子序列是非递增的还是非递减的;
- 我们在遍历过程中会用到下一个位置的值来判断是非递增还是非递减,那最后一个位置该怎么办?
对于数组开头的相等子序列,我们可以直接跳过,因为这一段相等的序列可以加到后面的子序列中;
而对于最后一个位置,如果它不能和前面序列组成一个排序子序列,那就只能让它自己组成一个排序子序列了。

代码实现
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int arr[N];
int n;
int main() {cin >> n;for (int i = 0; i < n; i++) cin >> arr[i];int ret = 0;for (int i = 0; i < n; i++) {if (i == n - 1) { //数组最后一个位置ret++;break;}if (arr[i] < arr[i + 1]) {//非递增while (i < n && arr[i] <= arr[i + 1])i++;ret++;} else if (arr[i] > arr[i + 1]) {//非递减while (i < n && arr[i] >= arr[i + 1])i++;ret++;} else {//数组开始位置的相等子序列while (i < n && arr[i] == arr[i + 1])i++;}}cout << ret << endl;return 0;
}
二、消减整数
题目解析

这道题给定一个正整数
H,然后从1开始减,第一次减去1,之后每一次减去的数要么和上一次相等,要么是上一次的两倍;简单来说就是:
h每次减去一个数,x起始是1;之后每一h减去x或者2*x(x表示上次减去的数)。现在,最少需要几次才能将
h减到0。
算法思路
对于这道题,暴力解法:
h每次减去x或者2*x,让它一值减,直到h减到0或者<0。简单来说就是分情况讨论:第一次减去
1,之后分别考虑减去x和减去2*x的情况。这样时间复杂度和空间复杂度都太大了;并且
h每一次减也不一定会恰好等于0。
贪心优化:
这道题要我们求的是将x减到0的最少次数;
那如果我们的h减去某一个数是无法减到0的,那我们就不用去考虑它了;
所以,我们现在要考虑的是,
h减的过程中,减去x能否减到0;减去2*x能否减到0。这个也非常容易判断了,如果
h是x的整数倍,那减去x就肯定可以减到0;如果h是2*x的整数倍,那减去2*x就也能减到0。
现在有一个问题,如果h既是x的倍数,也是2*x的倍数, 那是减去x还是2*x呢?
很显然是减去
2*X,因为我们要求的是h减到0的最小次数,那可以是减去大的数次数更小啊。
所以我们整体思路就出来了,在减的过程中,判断h是2*x的倍数,如果是就减去2*x;如果不是就减去x。

代码实现
#include <iostream>
using namespace std;
int main()
{int t;cin>>t;while(t--){int n;cin>>n;n--;//第一次减去1int ret = 1,x = 1;while(n){if(n % (2*x) == 0)x*=2;n-=x;ret++;}cout<<ret<<endl;}return 0;
}
三、最长上升子序列(二)
题目解析

对于这道题,给定一个数组,然后我们要找到这个数组中最长严格上升子序列的长度;
严格上升子序列:一个数组删掉其中一些数(可以不删)之后,形成的新数组它是严格上升(非递减)的。
简单来说就是:一个数组的子序列,这个子序列是严格上升的。
现在我们要找到所有上升子序列中长度最长的子序列;然后返回它的长度。
算法思路
对于这道题,一眼看起,可以说毫无思路;这该如何去找啊?
细细看来:
我们要找所有严格上升的子序列,当我们遍历到某一个位置时,我们要知道这个位置的数据和前面位置的数据是否能够形成严格上升的子序列;所以我们就要知道这个位置前面有多少个严格上升的子序列,这个位置的数据能放到哪些子序列当中去?
所以我们就要记录:当前所有的严格上升子序列,以及子序列中的元素。
那我们如何去记录所有的严格上升子序列呢?
当遍历到一个位置时:
这个位置如果是大于等于前面所有位置的,那我们可以把这个位置的元素放到任意一个子序列的后面形成一个新的子序列;
但是,我们没有必要去把这个元素放到每一个子序列的后面形成新的子序列。
加入前面有子序列
1、1,2、1,2,4,当前位置数据是7,我们可以形成1,7、1,2,7和1,2,4,7三个新的子序列;但是我们可以发现长度为2的子序列有两个1,2和1,7,我们有必要把这两个长度一样的子序列都记录下来吗?很显然是不需要的,我们只需要记录长度为
n的子序列它最后一个元素最小的子序列即可所以,我们只需要按长度
n(1,2,3...n)记录子序列即可。
那问题又来了,我们要记录子序列中的所有元素吗?
比如
1、1,2、1,2,4、1,2,4,7,我们要记录子序列中的所有元素吗?当然也是没有必要的;当我们遍历一个位置时,我们只需要判断这个位置的能否和前面的子序列组成新的子序列;我们不需要关心这个子序列是什么,所以我们只需要保存子序列最后一个位置的元素即可。
那现在还有一个问题:遍历一个位置时,它可以与前面子序列形成新的子序列,但是长度不是最大的怎么办?
简答来说:现在有子序列
1、1,2、1,2,4、1,2,4,7四个子序列,现在遍历到某一个位置,这个位置的值是3;它可以和
1形成1,3但是最后一个元素是3是大于1,2的最后一个元素2的,我们可以不用考虑。它可以和
1,2形成1,2,3,它最后一个元素3是小于1,2,4最后一个元素4的,我们就要修改长度为3的子序列,将4修改成3。
OK啊,现在大致明白了这道题如何去解决;
但是我们要遍历一遍数组,而且还要去判断一个某一个位置是否能和前面子序列形成新的子序列,形成新的子序列是否比之前的子序列更好;那就要存放每一个长度的子序列对应的最后一个元素的值;时间复杂度那不就是O(n^2)了,题目明确要求时间复杂度是O(n log N)啊。
二分查找
所以这里我们要使用二分算法去优化查找。
当我们遍历到一个位置时,当这个位置的值是
>=dp[pos](大于长度最大的子序列的最后一个位置),它可以和长度最大的子序列形成一个新的子序列,长度就是pos+1,直接新增一个位置即可(dp[pos+1] = x)。但是如果这个位置的值是小于长度最大的子序列的最后一个位置,它可能可以和前面的某一个子序列形成新的子序列,而形成新的子序列的最后一个位置的值,一定是小于等于之前该长度的子序列最后一个位置的值的。
所以我们就要找到这个子序列;
我们按暴力查找它的时间复杂度是
O(n);但是我们仔细思考可以发现,我们存放的是长度为n的子序列的最后一个位置的值,那这个数组dp是不是就是非递减的了?所以我们就可以使用二分查找来搜索这个子序列,而我们要找的也就是
>=当前位置的值的区间左端点。

代码实现
class Solution {public:int dp[100001];int pos = 0;int LIS(vector<int>& a) {for (auto& e : a) {if (pos == 0 || e >= dp[pos])dp[++pos] = e;else {int l = 1, r = pos;while (l < r) {int mid = l + (r - l) / 2;if (dp[mid] >= e)r = mid;elsel = mid + 1;}dp[l] = e;}}return pos;}
};
到这里,本篇文章内容就结束了。
继续加油啊!!!
相关文章:

【C++】 —— 笔试刷题day_29
一、排序子序列 题目解析 一个数组的连续子序列,如果这个子序列是非递增或者非递减的;这个连续的子序列就是排序子序列。 现在给定一个数组,然后然我们判断这个子序列可以划分成多少个排序子序列。 例如:1 2 3 2 2 1 可以划分成 …...

Ruby 循环与迭代器
Ruby 循环与迭代器 循环迭代器timesuptostep 循环 。。。。 迭代器 迭代器本质上可以理解为是循环的一种类型 times 3.times do print "Ho! " end begin Ho! Ho! Ho! end上述代码表示我们对当前 block 部分中的内容循环三次。最终,我们打印出了三个…...

力扣-39.组合总和
题目描述 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的 同一个 数字可以 无限制重复被…...

优化 Element UI 表格样式,隐藏滚动条但保持滚动功能
优化 Element UI 表格样式,隐藏滚动条但保持滚动功能 前言 在基于 Element UI 的项目中,el-table 是非常常用的表格组件。默认情况下,表格的滚动条可能影响页面的美观,特别是在视觉设计上希望更简洁时。本文分享一段优化的 CSS …...
实现原理和源码细节是Java高并发面试和实战开发的重点)
线程池(ThreadPoolExecutor)实现原理和源码细节是Java高并发面试和实战开发的重点
一、线程池核心流程图 ----------------- | 提交任务 | submit/execute -----------------|v ----------------- | 判断核心线程数 | < corePoolSize? -----------------|Yes |Nov v [创建新线程] -----------------| 队列是否满&a…...

MongoTemplate 基础使用帮助手册
前言 MongoDB 是一种流行的 NoSQL 数据库,适合存储大量的非结构化数据。MongoTemplate 是 Spring Data MongoDB 中的一个核心组件,它提供了一组丰富的 API 来与 MongoDB 进行交互。它封装了许多常见的数据库操作,使开发者能够轻松执行 CRUD 操…...
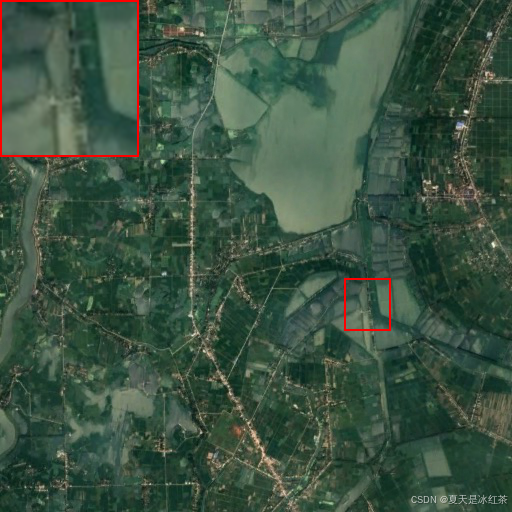
图像处理:预览并绘制图像细节
前言 因为最近在搞毕业论文的事情,要做出一下图像细节对比图,所以我这里写了两个脚本,一个用于框选并同时预览图像放大细节,可显示并返回框选图像的坐标,另外一个是输入框选图像的坐标并将放大的细节放置在图像中&…...

力扣热题——最长相邻不相等子序列 |
题目要求从字符串数组 words 中选出一个最长的子序列,使得该子序列中相邻字符串对应的 groups 数组中的值不同。通过贪心算法,可以高效地解决该问题。具体步骤为:初始化一个结果列表,遍历 words 数组,检查当前字符串的…...

【抽丝剥茧知识讲解】引入mybtis-plus后,mapper实现方式
目录 前言一、传统 Mapper 接口方式二、继承 BaseMapper 的方式三、自定义通用 Mapper 的方式四、使用 MyBatis-Plus 的 ActiveRecord 模式五、使用 MyBatis-Plus 的 IService 接口六、使用建议 前言 mapper文件,作为Mybatis框架中定义SQL语句和映射关系的配置文件&…...

ssti刷刷刷
[NewStarCTF 公开赛赛道]BabySSTI_One 测试发现过滤关键字,但是特殊符号中括号、双引号、点都能用 可以考虑拼接或者编码,这里使用拼接 ?name{{()["__cla"~"ss__"]}}?name{{()["__cla"~"ss__"]["__ba&…...

java+selenum专题(一)
环境搭建部署篇-> 1.简介 java版的selenium,介绍一下java selenium自动化测试。大致和pythonselenium自动化测试差不多。基于java和selenium做自动化测试,因此你必须会搭建基本的开发环境,掌握python基本的语法和一个IDE来进行开发&…...

物体雅克比、空间雅克比、解析雅克比、几何雅克比
在机器人学中,雅可比矩阵是连接广义坐标速度与末端执行器速度的关键工具。根据应用场景和参考系的不同,雅可比矩阵可分为物体雅可比(Body Jacobian)、空间雅可比(Space Jacobian)、解析雅可比(A…...

[逆向工程]DebugView捕获WPS日志?解析未运行WPS时Shell扩展加载的原因与解决方案(二十五)
[逆向工程]DebugView捕获WPS日志?解析未运行WPS时Shell扩展加载的原因与解决方案(二十五) 引言:一个“幽灵”般的日志问题 你是否在使用 DebugView 排查系统问题时,发现日志中频繁出现 WPS 相关模块(如 k…...

ACM模式用Scanner和System.out超时的解决方案和原理
Hi~!这里是奋斗的明志,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 🌱🌱个人主页:奋斗的明志 🌱🌱所属专栏:笔试强训 📚本系列文章为个人学…...

Java注解详解:从入门到实战应用篇
1. 引言 Java注解(Annotation)是JDK 5.0引入的一种元数据机制,用于为代码提供附加信息。它广泛应用于框架开发、代码生成、编译检查等领域。本文将从基础到实战,全面解析Java注解的核心概念和使用场景。 2. 注解基础概念 2.1 什…...

QML 属性动画、行为动画与预定义动画
目录 引言相关阅读本文使用的动画属性工程结构示例解析示例1:属性动画应用示例2:行为动画实现示例3:预定义动画 总结工程下载 引言 QML动画系统为界面元素提供了流畅的过渡效果。本文通过三个示例,结合属性动画(PropertyAnimatio…...

window nvidia-smi命令 Failed to initialize NVML: Unknown Error
如果驱动目录下的可以执行,那可能版本原因 "C:\Program Files\NVIDIA Corporation\NVSMI\nvidia-smi"复制"C:\Program Files\NVIDIA Corporation\NVSMI\nvidia-smi.exe"替换 C:\Windows\System32\nvidia-smi.exe 或者 把C:\Windows\System3…...
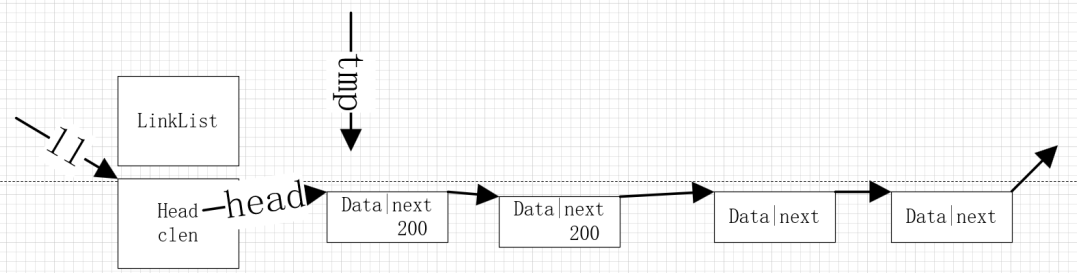
自学嵌入式 day19-数据结构 链表
二、线性表的链式存储 1.特点: (1)线性表链式存储结构的特点是一组任意的存储单位存储线性表的数据元素,存储单元可以是连续的,也可以不连续。可以被存储在任意内存未被占用的位置上。 (2)所以…...

东芝第3代SiC MOSFET助于降低应用中电源损耗
功率器件是管理和降低各种电子设备电能功耗以及实现碳中和社会的重要元器件。由于与比硅材料相比,碳化硅具有更高的电压和更低的损耗,因此碳化硅(SiC)被广泛视为下一代功率器件的材料。虽然碳化硅功率器件目前主要用于列车逆变器&…...

Vue 2.0学习
个人简介 👨💻个人主页: 魔术师 📖学习方向: 主攻前端方向,正逐渐往全栈发展 🚴个人状态: 研发工程师,现效力于政务服务网事业 🇨🇳人生格言&…...
详解)
Mendix 中的XPath 令牌(XPath Tokens)详解
在 Mendix 中,XPath 令牌(XPath Tokens) 是一种特殊的动态参数化查询技术,允许你在 XPath 表达式中使用变量或上下文相关的值,从而实现更灵活的查询逻辑。 1. 什么是 XPath 令牌? XPath 令牌是 Mendix 提…...

Spring Batch学习,和Spring Cloud Stream区别
Spring Batch学习,和Spring Cloud Stream区别 1. 使用Spring Initializr创建项目2. 使用步骤构建作业(Chunk 模式)🧩 场景说明🧰 1. 示例目录结构📄 2. 创建输入文件(users.csv)&…...

【技术原理】Linux 文件时间属性详解:Access、Modify、Change 的区别与联系
在 Linux 系统中,每个文件都有三个核心时间属性:Access Time (atime)、Modify Time (mtime) 和 Change Time (ctime)。它们分别记录文件不同维度的变更信息,以下是具体区别与联系: 一、定义与触发条件 时间属性定义触发条件示例A…...

k8s之LoadBalancer Service 解析
Kubernetes LoadBalancer Service 解析:IP与端口详解 服务类型与IP解析 Service 是 Kubernetes 中的资源类型,用来将一组 Pod 的应用作为网络服务公开。每个 Pod 都有自己的 IP,但是这个 IP 的生命周期与 Pod 生命周期一致,也就…...

Vue3项目使用ElDrawer后select方法不生效
Vue3 项目中 ElDrawer 内 ElSelect 下拉框 z-index 失效问题分析与解决方案 问题描述问题分析解决方案结论 问题描述 在 Vue3 项目中使用 Element Plus 的 ElDrawer 组件时,当在抽屉内部使用 ElSelect 组件,发现下拉选择框(dropdownÿ…...

PD 分离推理的加速大招,百度智能云网络基础设施和通信组件的优化实践
为了适应 PD 分离式推理部署架构,百度智能云从物理网络层面的「4us 端到端低时延」HPN 集群建设,到网络流量层面的设备配置和管理,再到通信组件和算子层面的优化,显著提升了上层推理服务的整体性能。 百度智能云在大规模 PD 分离…...

官方 Elasticsearch SQL NLPChina Elasticsearch SQL
官方的可以在kibana 控制台上进行查询: POST /_sql { “query”: “SELECT client_ip, status FROM logs-2024-05 WHERE status 500” } NLPChina Elasticsearch SQL就无法以在kibana 控制台上进行查询,但是可以使用postman接口进行查询:...

5月16日复盘-目标检测开端
5月16日复盘 一、图像处理之目标检测 1. 目标检测认知 Object Detection,是指在给定的图像或视频中检测出目标物体在图像中的位置和大小,并进行分类或识别等相关任务。 目标检测将目标的分割和识别合二为一。 What、Where 2. 使用场景 目标检测用于…...

读取toml, 合并,生成新文件
依次读取三个TOML文件并合并,后续文件覆盖之前的值,最终将结果写入新文件 import toml def deep_update(base_dict, update_dict): """ 递归合并字典,后续字典的值覆盖前者[6] """ for key, …...

mathematics-2024《Graph Convolutional Network for Image Restoration: A Survey》
推荐深蓝学院的《深度神经网络加速:cuDNN 与 TensorRT》,课程面向就业,细致讲解CUDA运算的理论支撑与实践,学完可以系统化掌握CUDA基础编程知识以及TensorRT实战,并且能够利用GPU开发高性能、高并发的软件系统…...
