python训练营打卡第26天
函数专题1:函数定义与参数
知识点回顾:
- 函数的定义
- 变量作用域:局部变量和全局变量
- 函数的参数类型:位置参数、默认参数、不定参数
- 传递参数的手段:关键词参数
- 传递参数的顺序:同时出现三种参数类型时
作业:
- 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 = π * radius² (可以使用 math.pi 作为 π 的值)
- 要求:函数接收一个位置参数 radius。计算半径为5、0、-1时候的面积
- 注意点:可以采取try-except 使函数变得更加稳健,如果传入的半径为负数,函数应该返回 0 (或者可以考虑引发一个ValueError,但为了简单起见,先返回0)。
import mathdef calculate_circle_area(radius):try:if radius < 0:raise ValueError("输入值无效")return math.pi*radius*radiusexcept ValueError as e:print(f"错误:{e}")return 0print(calculate_circle_area(5))#输出:78.53981633974483
print(calculate_circle_area(0))#输出:0
print(calculate_circle_area(-1))#输出: 错误:输入值无效题目2:计算矩形的面积
- 任务: 编写一个名为 calculate_rectangle_area 的函数,该函数接收矩形的长度 length 和宽度 width 作为参数,并返回矩形的面积。
- 公式: 矩形面积 = length * width
- 要求:函数接收两个位置参数 length 和 width。
- 函数返回计算得到的面积。
- 如果长度或宽度为负数,函数应该返回 0。
import math def calculate_rectangle_area(length, width):try:if length < 0 or width < 0:raise ValueError("输入值无效")return length * widthexcept ValueError as e:print (f"错误:{e}")return 0print(calculate_rectangle_area(5, 10))#输出:50 print(calculate_rectangle_area(0, 9))#输出:0 print(calculate_rectangle_area(5, 0))#输出:0 print(calculate_rectangle_area(-9, 10))#输出: 错误:输入值无效 print(calculate_rectangle_area(6, -5))#输出: 错误:输入值无效题目3:计算任意数量数字的平均值- 任务: 编写一个名为 calculate_average 的函数,该函数可以接收任意数量的数字作为参数(引入可变位置参数 (*args)),并返回它们的平均值。
- 要求:使用 *args 来接收所有传入的数字。
- 如果没有任何数字传入,函数应该返回 0。
- 函数返回计算得到的平均值。
import mathdef calculate_average(*args):if not args:return 0return sum(args) / len(args)print(calculate_average(1, 2, 3, 4, 5))#输出:3.0 print(calculate_average(7, 6, 9, 5))#输出:6.75 print(calculate_average(5, 6, 9))#输出:6.666666666666667 print(calculate_average(-5, -9, -6))#输出:-6.666666666666667
- 任务: 编写一个名为 print_user_info 的函数,该函数接收一个必需的参数 user_id,以及任意数量的额外用户信息(作为关键字参数)。
- 要求:
- user_id 是一个必需的位置参数。
- 使用 **kwargs 来接收额外的用户信息。
- 函数打印出用户ID,然后逐行打印所有提供的额外信息(键和值)。
- 函数不需要返回值
import mathdef print_user_info(user_id, **kwargs):print(f"用户ID: {user_id}")for key, value in kwargs.items():print(f"{key}: {value}")print_user_info(0319, 姓名='玉西', 年龄=24, 城市='沈阳')题目5:格式化几何图形描述
- 任务: 编写一个名为 describe_shape 的函数,该函数接收图形的名称 shape_name (必需),一个可选的 color (默认 “black”),以及任意数量的描述该图形尺寸的关键字参数 (例如 radius=5 对于圆,length=10, width=4 对于矩形)。
- 要求:shape_name 是必需的位置参数。
- color 是一个可选参数,默认值为 “black”。
- 使用 **kwargs 收集描述尺寸的参数。
- 函数返回一个描述字符串,格式如下:
- “A [color] [shape_name] with dimensions: [dim1_name]=[dim1_value], [dim2_name]=[dim2_value], …”如果 **kwargs 为空,则尺寸部分为 “with no specific dimensions.”
import mathdef describe_shap(shape_name, color='black', **kwargs):dimensions = ",".join([f"{key}={value}"for key, value in kwargs.items()])if dimensions:dimensions = f"with dimensions: {dimensions}"else:dimensions = "with no specific dimensions."return f"A {color} {shape_name} {dimensions}"print(describe_shap("square", color='red', side_length=6))
print(describe_shap("circle", color="yellow", radius=9))
print(describe_shap("triangle"))
print(describe_shap("retcangle", length=14, width=10))输出结果:
题目1:
78.53981633974483
0.0
错误:输入值无效
0题目2:
50
0
0
错误:输入值无效
0
错误:输入值无效
0题目3:
3.0
6.75
6.666666666666667
-6.666666666666667题目4:
用户ID: 319
姓名: 玉西
年龄: 24
城市: 沈阳题目5:
A yellow circle with dimensions: radius=9
A black triangle with no specific dimensions.
A black retcangle with dimensions: length=14,width=10
A red square with dimensions: side_length=6@浙大疏锦行
相关文章:

python训练营打卡第26天
函数专题1:函数定义与参数 知识点回顾: 函数的定义变量作用域:局部变量和全局变量函数的参数类型:位置参数、默认参数、不定参数传递参数的手段:关键词参数传递参数的顺序:同时出现三种参数类型时 作业&…...
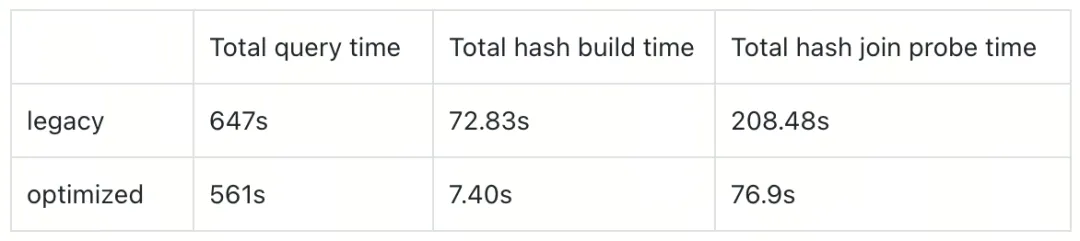
TiDB 中新 Hash Join 的设计与性能优化
原文来源: https://tidb.net/blog/11667c37 本文作者:徐飞 导读 在数据库管理系统(DBMS)中,连接操作(Join)是查询处理的核心环节之一,其性能直接影响到整个系统的响应速度和效率…...

1.共享内存(python共享内存实际案例,传输opencv frame)
主进程程序 send.py import cv2 import numpy as np from multiprocessing import shared_memory, resource_trackercap cv2.VideoCapture(0) if not cap.isOpened():print("无法打开 RTSP 流,请检查地址、网络连接或 GStreamer 配置。") else:# 创建共…...

网页常见水印实现方式
文章目录 1 明水印技术实现1.1 DOM覆盖方案1.2 Canvas动态渲染1.3 CSS伪元素方案2 暗水印技术解析2.1 空域LSB算法2.2 频域傅里叶变换3 防篡改机制设计3.1 MutationObserver防护3.2 Canvas指纹追踪4 前后端实现对比5 攻防博弈深度分析5.1 常见破解手段5.2 进阶防御策略6 选型近…...

oracle主备切换参考
主备正常切换操作参考:RAC两节点->单机 (rac和单机的操作区别:就是关闭其它节点,剩一个节点操作即可) 1.主库准备 检查状态 SQL> select inst_id,database_role,OPEN_MODE from gv$database; INST_ID DATA…...

Java大师成长计划之第25天:Spring生态与微服务架构之容错与断路器模式
📢 友情提示: 本文由银河易创AI(https://ai.eaigx.com)平台gpt-4-turbo模型辅助创作完成,旨在提供灵感参考与技术分享,文中关键数据、代码与结论建议通过官方渠道验证。 在微服务架构中,系统通常…...

【ARM】MDK如何将变量存储到指定内存地址
1、 文档目标 在嵌入式系统开发中,通过MDK(Microcontroller Development Kit)进行工程配置,将指定的变量存储到指定的内存地址上是一项非常重要的技术。这项操作不仅能够满足特定硬件架构的需求,还能优化系统的性能和…...
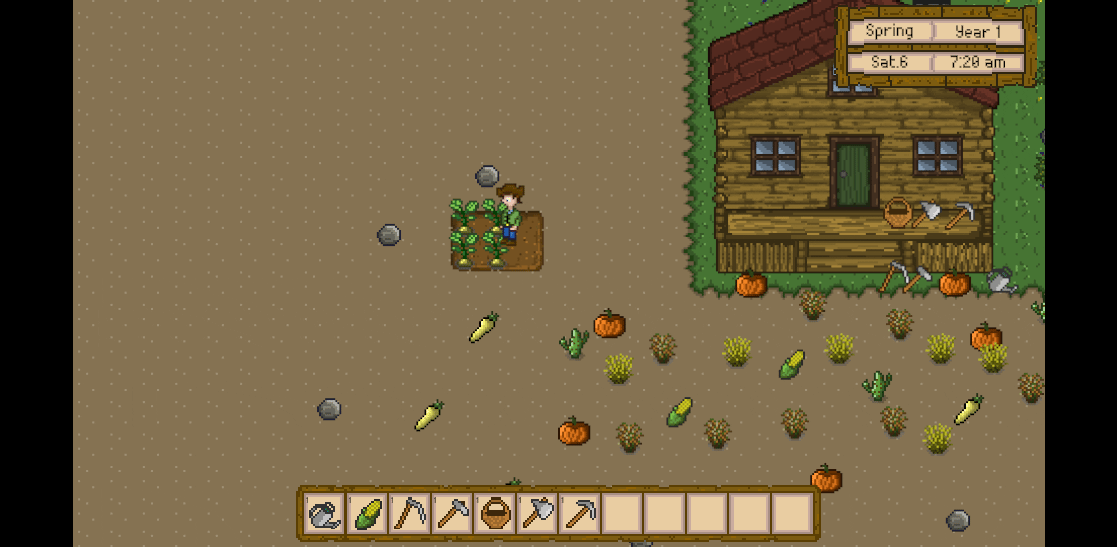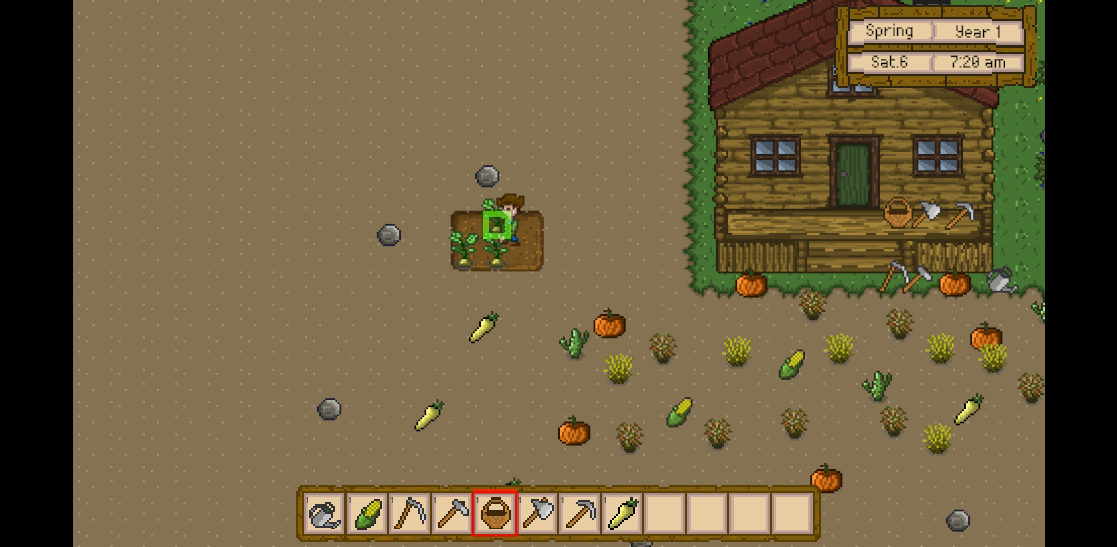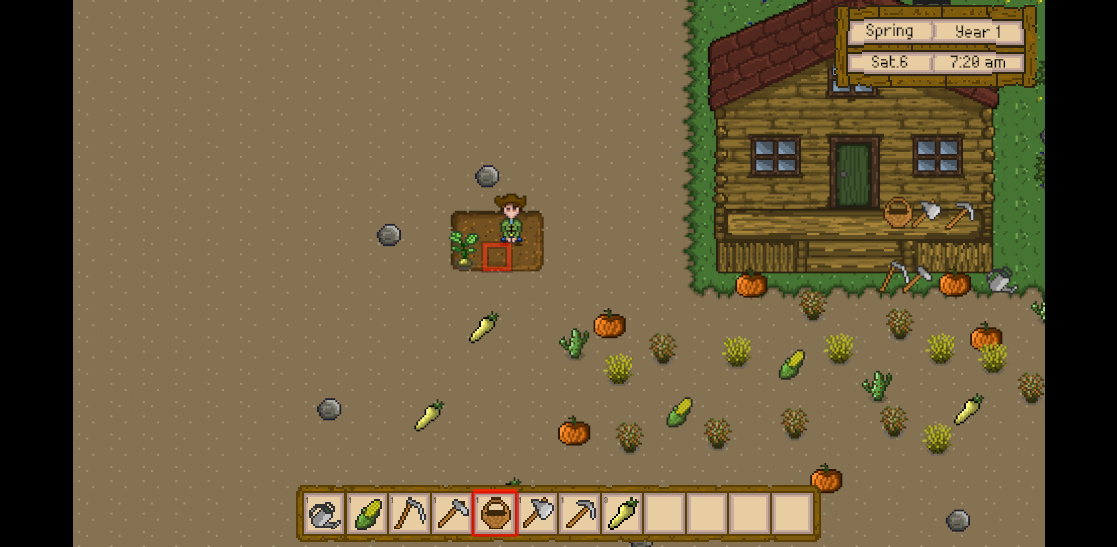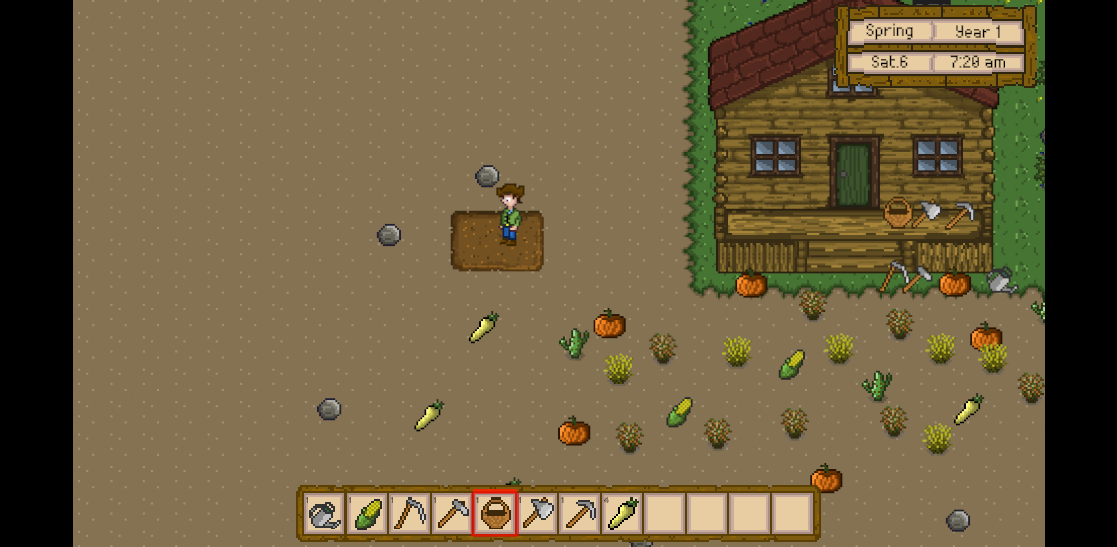
Unity3D仿星露谷物语开发44之收集农作物
1、目标 在土地中挖掘后,洒下种子后逐渐成长,然后使用篮子收集成熟后的农作物,工具栏中也会相应地增加该农作物。 2、修改CropStandard的参数 Assets -> Prefabs -> Crop下的CropStandard,修改其Box Collider 2D的Size(Y…...

langchain—chatchat
署部 下载项目 git clone --recursive https://github.com/chatchat-space/Langchain-Chatchat.git 进入目录 cd Langchain-Chatchat anaconda环境准备 创建python环境 conda create -n langchain_env python3.10 -y 激活环境 conda activate langchain_env 验证pyhton环境…...
 % mod,保证mod是质数)
经典算法 求C(N, K) % mod,保证mod是质数
求C(N, K) % mod,保证mod是质数 问题描述 给你三个整数N,K,mod保证mod是一个质数,求组合数C(N, K) % mod。 输入描述 输入有多组,输入第一行为两个整数T,mod。接下来2 - T 1行,每行输入N, K。 输出描…...

【LeetCode 热题 100】二叉树的最大深度 / 翻转二叉树 / 二叉树的直径 / 验证二叉搜索树
⭐️个人主页:小羊 ⭐️所属专栏:LeetCode 热题 100 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 二叉树的中序遍历二叉树的最大深度翻转二叉树对称二叉树二叉树的直径二叉树的层序遍历将有序数组转换为二叉搜索树验…...

关于软件测试开发的一些有趣的知识
文章目录 一、什么是测试?二、为什么要软件测试软件测试三、测试的岗位有哪些四 、软件测试和开发的区别五、走测试岗位为什么还要学开发。4、优秀的测试人员具备的素质我为什么走测试岗位 一、什么是测试? 其实这个问题说简单也不简单,说难…...

uni-app 开发HarmonyOS的鸿蒙影视项目分享:从实战案例到开源后台
最近,HBuilderX 新版本发布,带来了令人兴奋的消息——uni-app 现在支持 Harmony Next 平台的 App 开发。这对于开发者来说无疑是一个巨大的福音,意味着使用熟悉的 Vue 3 语法和开发框架,就可以为鸿蒙生态贡献自己的力量。 前言 作…...

售前工作.工作流程和工具
第一部分 售前解决方案及技术建议书的制作 售前解决方案编写的标准操作步骤SOP: 售前解决方案写作方法_哔哩哔哩_bilibili 第二部分 投标过程关键活动--商务标技术方案 1. 按项目管理--售前销售项目立项 销售活动和销售线索的跟踪流程和工具 1)拿到标书ÿ…...
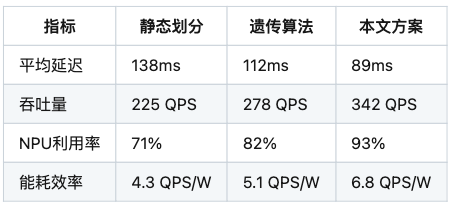
GPU与NPU异构计算任务划分算法研究:基于强化学习的Transformer负载均衡实践
点击 “AladdinEdu,同学们用得起的【H卡】算力平台”,H卡级别算力,按量计费,灵活弹性,顶级配置,学生专属优惠。 引言 在边缘计算与AI推理场景中,GPU-NPU异构计算架构已成为突破算力瓶颈的关键技…...

学习ai课程大纲
以下是一个通用的 AI 课程大纲,涵盖从基础到进阶的核心内容,适用于大学课程或自学规划。你可以根据自身需求(如入门、进阶、专项方向)调整内容和深度。 人工智能(AI)课程大纲 第一部分:基础理论…...

基于CentOS7制作OpenSSL 1.1的RPM包
背景:CentOS7 已经不再维护了,有时候需要升级某些组件,网上却没有相关的资源了。尤其是制作OpenSSH 9.6 的RPM包,就会要求OpenSSL为1.1的版本。基于此,还是自己制作吧,以下是踩坑过程。 1、官网提供的源码包…...

数据分析_Python
1 分析内容 1.1 数据的整体概述 提供数据集的基本信息,包括数据量、时间跨度、地理范围和主要字段. import pandas as pd# 创建示例数据 data {姓名: [张三, 李四, 王五, 赵六, 钱七, 孙八, 周九, 吴十],年龄: [25, 30, 35, 40, 45, 50, 55, 60],性别: [男, 男, 女, 女, 男,…...

TCP/UDP协议原理和区别 笔记
从简单到难吧 区别就是TCP一般用于安全稳定的需求,UDP一般用于不那么需要完全数据的需求,比如说直播,视频等。 再然后就是TPC性能慢于UDP。 再然后我们看TCP的原理(三次握手,数据传输,四次挥手࿰…...

深入浅出:C++数据处理类与计算机网络的巧妙类比
深入浅出:C数据处理类与计算机网络的巧妙类比 引言 在计算机编程中,我们常常会遇到一些看似简单的代码结构,却能巧妙地映射到复杂的计算机网络概念中。本文将通过一个简单的C数据处理类,探讨其与计算机网络中硬件设备和协议的类…...

【滑动窗口】LeetCode 209题解 | 长度最小的子数组
长度最小的子数组 前言:滑动窗口一、题目链接二、题目三、算法原理解法一:暴力枚举解法二:利用单调性,用滑动窗口解决问题那么怎么用滑动窗口解决问题?分析滑动窗口的时间复杂度 四、编写代码 前言:滑动窗口…...

在RK3588上使用NCNN和Vulkan加速ResNet50推理全流程
在RK3588上使用NCNN和Vulkan加速ResNet50推理全流程 前言:为什么需要关注移动端AI推理一、环境准备与框架编译1.1 获取NCNN源码1.2 安装必要依赖1.3 编译NCNN二、模型导出与转换2.1 生成ONNX模型2.2 转换NCNN格式三、模型量化加速3.1 生成校准数据3.2 执行量化操作四、性能测试…...

【ant design】ant-design-vue 4.0实现主题色切换
官网:Ant Design Vue — An enterprise-class UI components based on Ant Design and Vue.js 我图方便,直接在 app.vue 中加入的 <div class"app-content" v-bind:class"appOption.appContentClass"><a-config-provider…...

Android 图片自动拉伸不变形,点九
要让 UI 设计师 制作 Android 用的点九图(.9.png),可以按照以下流程和要求进行: 🧩 一、什么是点九图? 点九图(NinePatch)是一种特殊的 PNG 图像,用于在 Android 中根据…...

电子电路:什么是色环电阻器,怎么识别和计算阻值?
识别和计算色环电阻的阻值需要掌握颜色编码规则和基本步骤。以下是具体方法及窍门: 一、色环电阻的基本规则 色环数量: 4环电阻:前2环为有效数字,第3环为倍乘(10ⁿ),第4环为误差。5环电阻:前3环为有效数字,第4环为倍乘,第5环为误差。6环电阻(较少见):前3环为有效数…...

LeetCode Hot100刷题——轮转数组
56. 轮转数组 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: …...

Python绘制南丁格尔玫瑰图:从入门到实战
Python绘制南丁格尔玫瑰图:从入门到实战 引言 南丁格尔玫瑰图(Nightingale Rose Chart),也被称为极区图(Polar Area Chart),是一种独特的数据可视化方式。这种图表由弗洛伦斯南丁格尔ÿ…...

概率与期望总结
一、概率 概念:无需多言;几个公式( Ω \Omega Ω 表示整个样本空间): 以下公式均有 A , B ⊆ Ω , 且 P ( A ) , P ( B ) > 0. P ( A ∪ B ) P ( A ) P ( B ) − P ( A ∩ B ) , P ( A ∣ B ) P ( A B ) P ( B…...

炼丹学习笔记3---ubuntu2004部署运行openpcdet记录
前言 环境 cuda 11.3 python 3.8 ubuntu2004 一、cuda环境检测 ylhy:~/code_ws/OpenPCDet/tools$ nvcc -V nvcc: NVIDIA (R) Cuda compiler driver Copyright (c) 2005-2021 NVIDIA Corporation Built on Sun_Mar_21_19:15:46_PDT_2021 Cuda compilation tools, release 11.3…...

深入解析BGP路由反射器与联邦:突破IBGP全连接限制的两种方案
一、引言:大型BGP网络的挑战 在大型BGP网络架构中,传统的IBGP全连接架构会带来严重的扩展性问题。当网络中存在N台路由器时,需要维护N*(N-1)/2个IBGP连接,这对设备资源和运维管理都是巨大挑战。本文将深入解析两种主流解决方案&a…...
