当前位置： 首页 > article >正文

信息系统项目管理师高级-软考高项案例分析备考指南（2023年案例分析）

article 2025/9/22 7:49:03

个人笔记整理---仅供参考

计算题
案例分析里的计算题就是进度、挣值分析、预测技术。主要考査的知识点有:找关键路径、求总工期、自由时差、总时差、进度压缩资源平滑、挣值计算、预测计算。计算题是一定要拿下的，做计算题要保持头脑清晰，认真读题把PV、EV、AC找出来，知道是典型和非典型。另外，对于进度的计算比如简单的找关键路径、求总工期、自由时差、总时差是不需要写过程的。对于别的内容，需要写过程，写公式，就算你最后没全部算出来，也会得到过程分。

方法一---六时标网络图

方法二---双代号时标网络图：

自由时差看后面波浪线的长度

总时差指从当前活动往后数所有波浪线长度之和的最小值

D活动的总时差为0

eg：项目经理组织了制定了项目管理计划

错误：1、干系人不全面   2、项目管理计划不应该由项目经理独自制定

3、项目管理计划有没有经过评审

4、项目管理计划内容不全面

相关文章：

信息系统项目管理师高级-软考高项案例分析备考指南（2023年案例分析）

个人笔记整理---仅供参考 计算题 案例分析里的计算题就是进度、挣值分析、预测技术。主要考査的知识点有:找关键路径、求总工期、自由时差、总时差、进度压缩资源平滑、挣值计算、预测计算。计算题是一定要拿下的，做计算题要保持头脑清晰，认真读题把PV、…...

编程日记 2025/9/16 19:32:49

stack和queue简单模拟实现

stackreverse_iteratorqueuepriority_queue仿函数具体代码 stack Stacks are a type of container adaptor, specifically designed to operate in a LIFO context (last-in first-out), where elements are inserted and extracted only from one end of the container. 上述描…...

编程日记 2025/7/2 7:13:28

如何安装双系统？即windows已经安装，如何安装ubuntu 22.04LTS

在已安装 Windows 的电脑上安装 Ubuntu 22.04 LTS 双系统，需通过 分区调整、UEFI/BIOS 设置 和 引导管理 实现。以下是详细步骤： 一、准备工作 备份数据 • 备份 Windows 中的重要文件（防止分区操作失误导致数据丢失）。 下载 Ubu…...

编程日记 2025/6/10 10:21:19

产品经理入门（2）产品体验报告

产品体验报告大纲：重点在产品体验——优点。 1.产品概括 可以从各大平台搜产品介绍。 2.市场分析 按照产品方向分析各个指标——包括有效使用时间,市场规模等。 3. 用户分析——对用户通过各项指标画像。 4.产品体验——对各项功能与设计的体验。 5.报告总结...

编程日记 2025/9/21 14:47:14

C43-指针与数组

一 定义一个指针变量指向数组 1.途径一:指向数组首元素的地址 代码示例: #include <stdio.h> int main() {int arr[3]{2,4,5};int *p;p&arr[0];printf("该数组的首元素是:%d",*p);return 0; }成果展示: 报错与总结: 给指针变量赋值时,未在数组首元素前输…...

编程日记 2025/9/18 0:42:04

UDP--DDR--SFP,FPGA实现之ddr读写控制模块

DDR读写控制模块实现介绍 由于该模块接口数量较多&#xff0c;为了详细说明模块实现&#xff0c;采用文字流程进行介绍 上级模块传输数据到来捕捉数据有效上升沿传输写指令&#xff0c;写有效&#xff0c;写指令成功被下一级模块缓存&#xff0c;进行写地址一次读写长度&…...

编程日记 2025/9/18 23:16:04

云计算与大数据进阶 | 26、解锁云架构核心：深度解析可扩展数据库的5大策略与挑战（上）

在云应用/服务的 5 层架构里&#xff0c;数据库服务层稳坐第 4 把交椅&#xff0c;堪称其中的 “硬核担当”。它的复杂程度常常让人望而生畏&#xff0c;不少人都将它视为整个架构中的 “终极挑战”。 不过&#xff0c;也有人觉得可扩展存储系统才是最难啃的 “硬骨头”&#…...

编程日记 2025/9/14 11:13:40

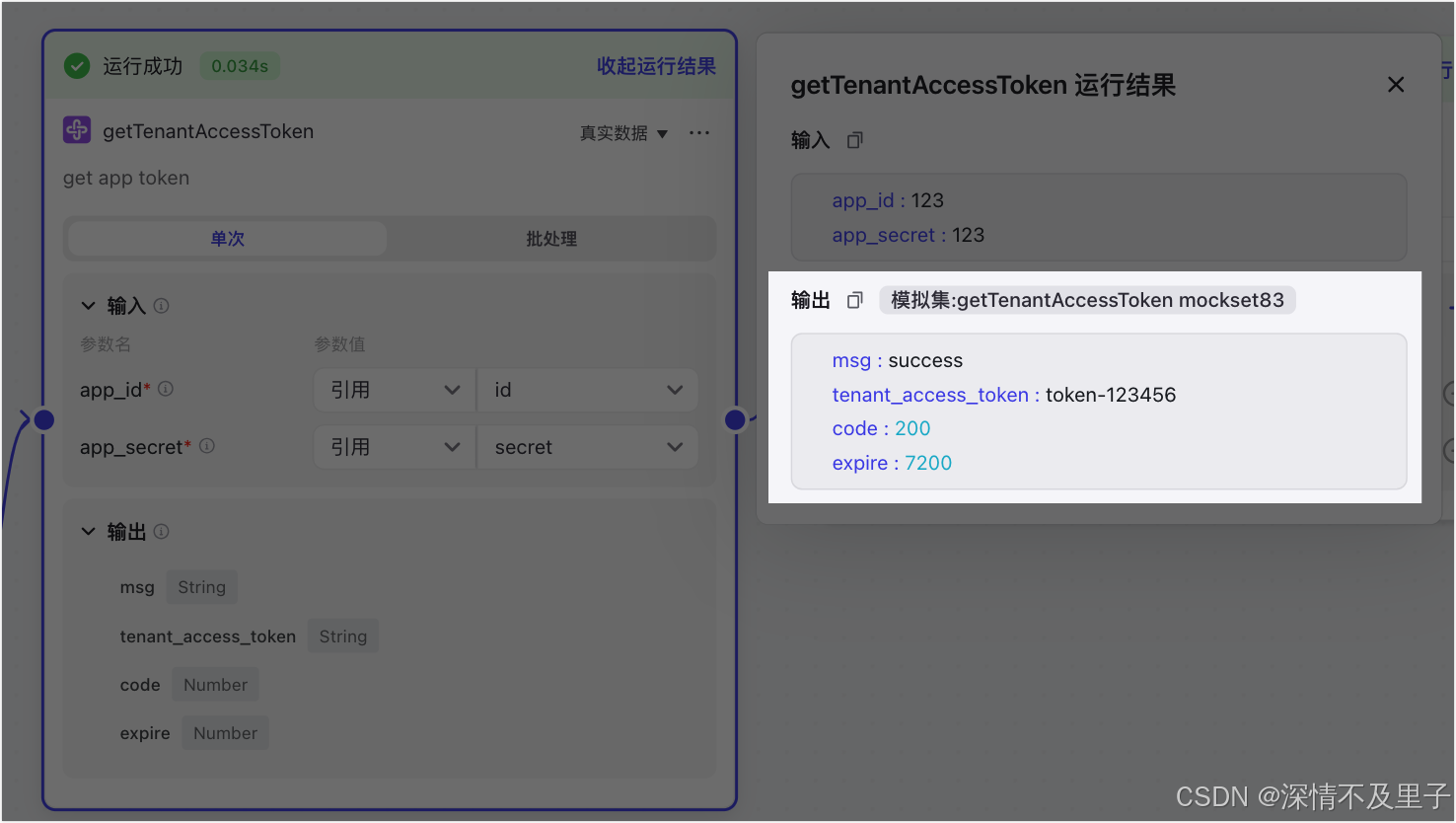
AI Agent | Coze 插件使用指南：从功能解析到实操步骤

一、前言 在人工智能技术飞速发展的今天&#xff0c;低代码开发模式正成为构建智能应用的主流趋势。对于希望快速搭建 AI Bot 的开发者和业务人员而言&#xff0c;coze作为一款强大的低代码 AI 开发平台&#xff0c;凭借其高度模块化的插件体系脱颖而出。这些插件就像搭建智能…...

编程日记 2025/9/21 13:29:26

06、基础入门-SpringBoot-依赖管理特性

06、基础入门-SpringBoot-依赖管理特性 Spring Boot 的依赖管理特性是其核心优势之一&#xff0c;极大地简化了项目的构建和维护过程。以下是其主要特点&#xff1a; ## 1. 父项目依赖管理 ### 1.1 继承 spring-boot-starter-parent 在 pom.xml 文件中&#xff0c;通过继承 spr…...

编程日记 2025/7/13 1:59:02

MK米客方德SD NAND:无人机存储的高效解决方案

在无人机技术迅猛发展的当下&#xff0c;飞控系统的数据记录对于飞行性能剖析、故障排查以及飞行安全保障极为关键。以往&#xff0c;SD 卡是飞控 LOG 记录常见的存储介质&#xff0c;但随着技术的革新&#xff0c;新的存储方案不断涌现。本文聚焦于以 ESP32 芯片为主控制器的无…...

编程日记 2025/9/18 10:19:25

【vscode】解决vscode无法安装远程服务器插件问题，显示正在安装

文章目录 现状分析采用VSIX离线安装第一步&#xff1a;离线下载插件包第二步&#xff1a;把下载好的插件文件上传到远程服务器上第三步&#xff1a;在windows下打开vscode&#xff0c;并链接远端&#xff0c;进行安装 现状分析 vscode无法远程安装扩展插件&#xff0c;显示正在…...

编程日记 2025/9/3 18:36:58

1688 数据接口调用秘籍：高效获取商品实时信息的开发指南

在电商行业竞争白热化的当下&#xff0c;企业想要抢占市场先机&#xff0c;实时掌握商品信息至关重要。作为国内 B2B 电商巨头&#xff0c;1688 平台汇聚海量商品资源&#xff0c;通过高效调用其数据接口获取商品实时信息&#xff0c;能为企业价格策略制定、库存管理、竞品分析…...

编程日记 2025/6/20 12:52:44

【Spring】Spring的请求处理

欢迎来到啾啾的博客&#x1f431;。 记录学习点滴。分享工作思考和实用技巧&#xff0c;偶尔也分享一些杂谈&#x1f4ac;。 欢迎评论交流&#xff0c;感谢您的阅读&#x1f604;。 目录 引言HTTP/HTTPS协议Spring Web与Spring Web MVCSpring WebFlux 自定义的TPC/IP协议FTP、S…...

编程日记 2025/9/18 0:41:36

粒子群算法（PSO算法）

粒子群算法概述 1.粒子群优化算法&#xff08;Particle Swarm Optimization&#xff0c;简称PSO&#xff09;。粒子群优化算法是在1995年由Kennedy博士和Eberhart博士一起提出的&#xff0c;它源于对鸟群捕食行为的研究。 2.基本核心是利用群体中的个体对信息的共享从而使得整…...

编程日记 2025/9/18 11:24:17

git提交库常用词

新功能 feat修改BUG fix文档修改 docs格式修改 style重构 refactor性能提升 perf测试 test构建系统 build对CI配置文件修改 ci修改构建流程、或增加依赖库、工具 chore回滚版本 revert...

编程日记 2025/9/20 5:08:21

LLM智能体新纪元：深入解析MCP与A2A协议，赋能智能自动化协作

LLM智能体&#xff08;LLM agents&#xff09;是能够自主行动以实现特定目标的AI系统。在实际应用中&#xff0c;智能体能够将用户请求拆解为多个步骤&#xff0c;利用知识库或API获取数据&#xff0c;最终整合出答案。这让智能体相比于传统独立聊天机器人拥有更强大的能力——…...

编程日记 2025/9/18 8:06:07

SAP学习笔记 - 开发豆知识01 - CDS SDK命令出乱码 （cds init CAP-Test03 --add java）

1&#xff0c;现象 安装完VSCode以及各种需要的插件&#xff08;比如SAP CDS Language Support&#xff09;&#xff0c;就可以做CAP开发。 用这个命令创建Project&#xff1a;cds init CAP-Test03 --add java 然后出来一个乱码错误 adding java The derived package name c…...

编程日记 2025/9/17 13:15:45

（C语言）超市管理系统 （正式版）（指针）（数据结构）（清屏操作）（文件读写）（网页版预告）（html）（js）（json）

目录 前言&#xff1a; 源代码&#xff1a; product.h product.c fileio.h fileio.c main.c json_export.h json_export.c tasks.json idex.html script.js 相关步骤&#xff1a; 第一步&#xff1a; 第二步&#xff1a; 第三步&#xff1a; 第四步&#xff1a; 第五步…...

编程日记 2025/9/19 2:15:54

进阶-数据结构部分：​​​​​​​2、常用排序算法

飞书文档https://x509p6c8to.feishu.cn/wiki/FfpIwIPtviMMb4kAn3Sc40ABnUh 常用排序算法 这几种算法都是常见的排序算法&#xff0c;它们的优劣和适用场景如下&#xff1a; 冒泡排序&#xff08;Bubble Sort&#xff09;&#xff1a;简单易懂&#xff0c;时间复杂度较高&…...

编程日记 2025/9/18 0:41:10

解决 Three.js Raycaster 点击位置与实际交点偏差问题

当使用 Three.js 的 Raycaster 时&#xff0c;如果发现点击位置与显示的碰撞点之间存在较大偏差&#xff0c;这通常是由于坐标系统不匹配或参数设置不正确导致的。以下是系统性的排查和解决方案&#xff1a; 1. 检查鼠标坐标转换 最常见的偏差原因是鼠标坐标到标准化设备坐标…...

编程日记 2025/5/26 17:36:15

25、DeepSeek-R1论文笔记

DeepSeek-R1论文笔记 1、研究背景与核心目标2、核心模型与技术路线3、蒸馏技术与小模型优化4、训练过程简介5、COT思维链&#xff08;Chain of Thought&#xff09;6、强化学习算法&#xff08;GRPO&#xff09;7、冷启动**1. 冷启动的目的****2. 冷启动的实现步骤****3. 冷启动…...

编程日记 2025/9/14 11:55:47

LeetCode --- 156双周赛

题目列表 3541. 找到频率最高的元音和辅音 3542. 将所有元素变为 0 的最少操作次数 3543. K 条边路径的最大边权和 3544. 子树反转和 一、找到频率最高的元音和辅音 分别统计元音和辅音的出现次数最大值&#xff0c;然后相加即可&#xff0c;代码如下 // C class Solution {…...

编程日记 2025/9/17 13:21:56

模型量化AWQ和GPTQ哪种效果好?

环境&#xff1a; AWQ GPTQ 问题描述&#xff1a; 模型量化AWQ和GPTQ哪种效果好? 解决方案&#xff1a; 关于AWQ&#xff08;Adaptive Weight Quantization&#xff09;和GPTQ&#xff08;Generative Pre-trained Transformer Quantization&#xff09;这两种量化方法的…...

编程日记 2025/5/27 9:31:37

npm 报错 gyp verb `which` failed Error: not found: python2 解决方案

一、背景 npm 安装依赖报如下错&#xff1a; gyp verb check python checking for Python executable "python2" in the PATH gyp verb which failed Error: not found: python2 一眼看过去都觉得是Python环境问题&#xff0c;其实并不是你python环境问题&#xf…...

编程日记 2025/9/18 5:16:57

初识Linux · IP协议· 下

目录 前言&#xff1a; 内网IP和公网IP 内网IP 公网IP 路由 前言&#xff1a; 前文我们介绍了IP协议的协议头&#xff0c;通过源码等方式我们理解了IP协议中的字段&#xff0c;比如8位协议&#xff0c;比如通过环回问题引出的8位最大生存时间&#xff0c;比如8位协议&…...

编程日记 2025/9/21 16:21:26

5.27本日总结

一、英语 复习list2list29 二、数学 学习14讲部分内容 三、408 学习计组1.2内容 四、总结 高数和计网明天结束当前章节&#xff0c;计网内容学完之后主要学习计组和操作系统 五、明日计划 英语&#xff1a;复习lsit3list28&#xff0c;完成07年第二篇阅读 数学&#…...

编程日记 2025/5/25 8:34:26

JavaScript基础-创建对象的三种方式

在JavaScript中&#xff0c;对象是构建复杂数据结构和实现面向对象编程的核心。掌握如何创建对象对于每个开发者来说都是必不可少的技能。本文将介绍创建JavaScript对象的三种主要方式&#xff1a;对象字面量、构造函数以及类&#xff08;ES6引入&#xff09;&#xff0c;并探讨…...

编程日记 2025/6/14 0:23:28

JAVA的常见API文档(上)

游戏打包 注意API文档中的方法不需要记忆&#xff01;&#xff01; 了解之后如果需要可以查询API文档 对Math的方法总结&#xff1a; 运用刚学的Math方法加快代码的运行效率 可以减少循环次数 找规律&#xff1a; 发现因子有规律&#xff1a; 必定一个大于平方根&#xff0c;…...

编程日记 2025/9/22 1:14:30

JavaScript 中的 for...in 和 for...of 循环详解

在 JavaScript 中&#xff0c;for...in 和 for...of 是两种常用的循环结构&#xff0c;但它们有着不同的用途和行为。很多初学者容易混淆这两者&#xff0c;本文将详细解析它们的区别、适用场景以及注意事项。 目录 for…in 循环 基本用法遍历对象属性注意事项 for…of 循环 …...

编程日记 2025/6/7 8:51:18

AtCoder AT_abc406_c [ABC406C] ~

前言 除了 A 题&#xff0c;唯一一道一遍过的题。 题目大意 我们定义满足以下所有条件的一个长度为 N N N 的序列 A ( A 1 , A 2 , … , A N ) A(A_1,A_2,\dots,A_N) A(A1​,A2​,…,AN​) 为波浪序列&#xff1a; N ≥ 4 N\ge4 N≥4&#xff08;其实满足后面就必须满足这…...

编程日记 2025/6/14 12:43:25