【数据结构篇】排序1(插入排序与选择排序)
注:本文以排升序为例
常见的排序算法:

目录:
一 直接插入排序:
1.1 基本思想:
1.2 代码:
1.3 复杂度:
二 希尔排序(直接插入排序的优化):
2.1 基本思想:
2.2 代码:
2.3 复杂度:
三 直接选择排序:
3.1 基本思想:
3.2 代码:
3.3 复杂度:
四 堆排序:
一 直接插入排序:
1.1 基本思想:
直接插入排序是⼀种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到⼀个已经排好序的有序序列中,直到所有的记录插入完为止,得到⼀个新的有序序列。
- 实际我们玩扑克牌时就用到了这一思想

动图:
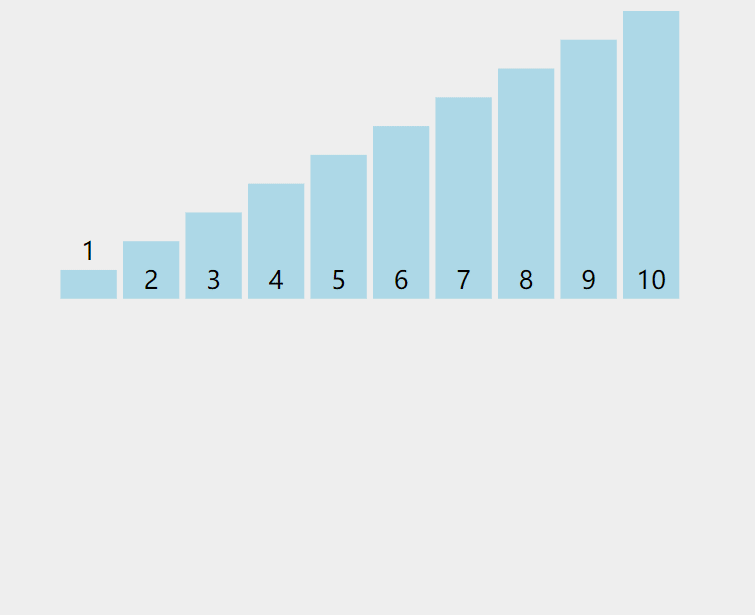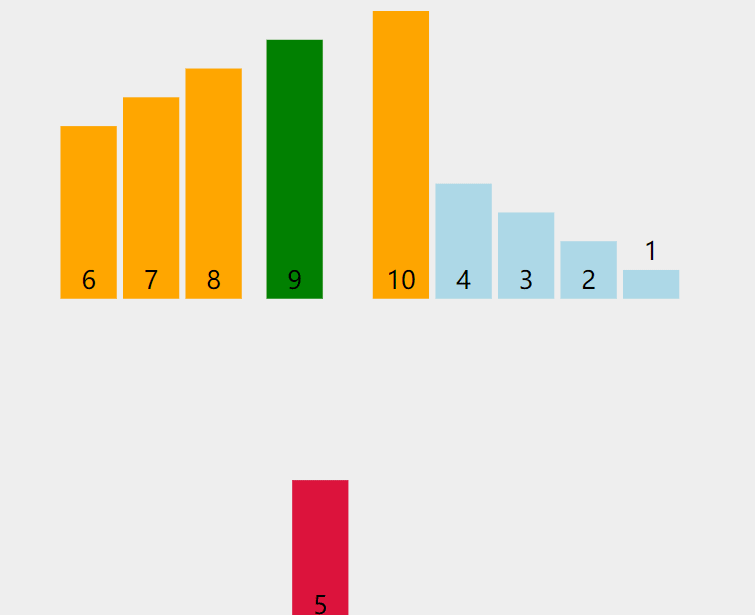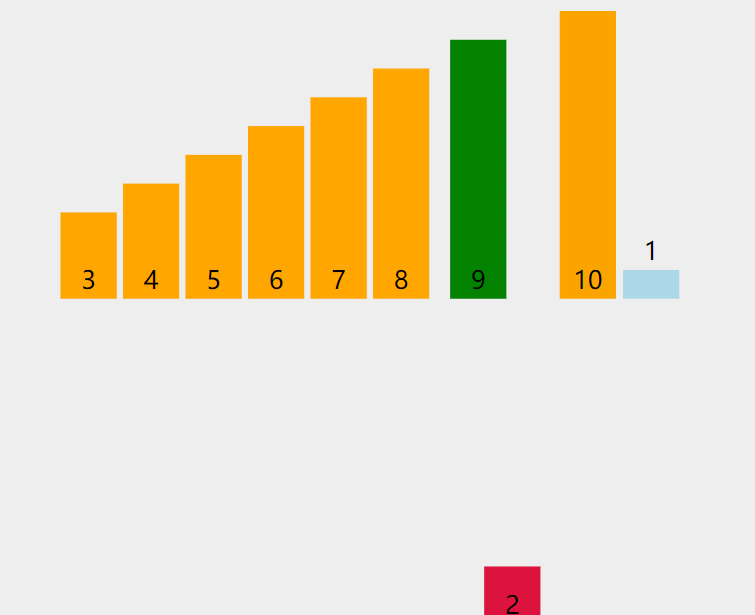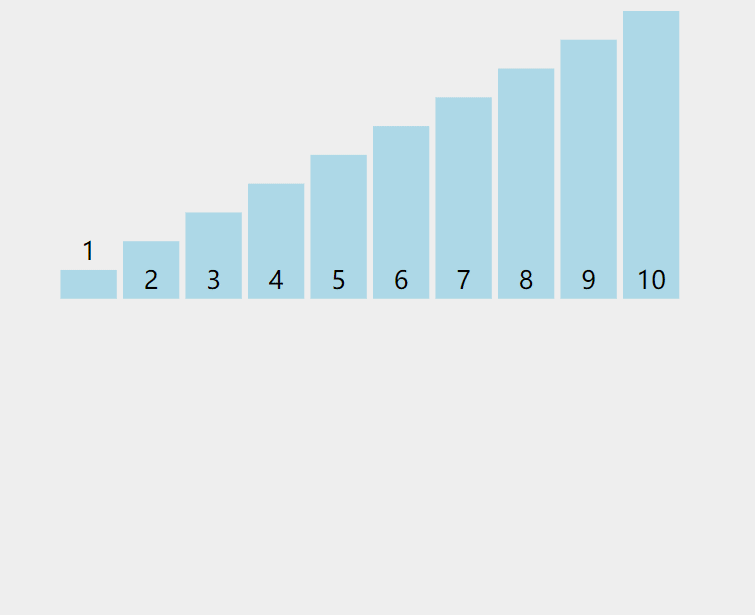
解释:当插入第 i(i>=1) 个元素时,前面的 array[0],array[1],…,array[i-1] 已经排好序,此时⽤ array[i] 的排序码与 array[i-1],array[i-2],… 的排序码顺序进行比较,找到插入位置即将 array[i] 插入,原来位置上的元素顺序后移。
1.2 代码:
//直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n-1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}end:指向有序序列的最后一个数据:初始为0,末态为n-2
tmp:有序序列后的第一个待排序数据:初始为1,末态为n-1
以一次循环为例:
将tmp与end位置数据进行比较,若end处更大,将end位置数据移到end+1处,end--,继续让end-1处数据与tmp比较
否则直接跳出循环,此时end+1位置为空,需要放入tmp最坏的情况:当end为0处数据移到end为1处,此时end变为-1,需要跳出循环,并将tmp放到0处
1.3 复杂度:
元素集合越接近有序,直接插入排序算法的时间效率越高。
1.时间复杂度:O(N^2)
2.空间复杂度:O(1)
二 希尔排序(直接插入排序的优化):
在直接插入排序中我们发现,元素越无序,直接插入排序算法时间效率越低(因为比较次数越多)。特别是当数组为降序,我们要排升序,此时数组的相对无序程度达到了最大,时间复杂度也到了最大。所以D.L.Shell在1959年提出了希尔排序。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
2.1 基本思想:
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定⼀个整数(通常是gap=n/3+1),把 待排序⽂件所有记录分成各组,所有的距离相等的记录分在同⼀组内,并对每⼀组内的记录进⾏排序,然后gap=gap/3+1得到下⼀个整数,再将数组分成各组,进行插入排序,当gap=1时,就相当于 直接插入排序。它是在直接插入排序算法的基础上进行改进⽽来的,综合来说它的效率肯定是要⾼于直接插入排序算法的。
以排序数组为例:

2.2 代码:
//希尔排序
//希尔排序时间复杂度大约为:O(n^1.3)
void ShellSort(int* arr, int n)
{int gap = n;//6while (gap > 1){gap = gap / 3 + 1;//保证最后一次gap一定为1for (int i = 0; i < n - gap; i++){int end = i;//n-gap-1int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else {break;}}arr[end + gap] = tmp;}}
}直接插入排序法的改进,其在许多地方有相似之处:
一次预排序
从下标为0的元素开始,每隔gap-1个数据取数据分到一组,从取数据的方式我们可以得出以下结论:
总共有gap组(0-(gap-1)的元素为每一组的头元素)
每组有n/gap或n/gap+1个数据
每一次排序我们排的是end和end+gap(即tmp)处的元素,保证每次排序都是在同一组内排
end初始为0可得tmp初始为gap,tmp末态为n-1可得end末态为n-1-gap
在一组内进行的是直接插入排序,只不过把距离从1换为gap,全部换一下就行了,思路是一样的,每次预排序结束后,让gap/3+1,加一保证最后一次排序gap为1,否则无法保证最后一次是直接插入排序
2.3 复杂度:
1.时间复杂度:最好O(N^1.3),最坏O(N^2)
2.空间复杂度:O(1)
三 直接选择排序:
3.1 基本思想:
1.在元素集合 array[i]–array[n-1] 中选择关键码最大(小)的数据元素
2.若它不是这组元素中的最后一个(第⼀个)元素,则将它与这组元素中的最后⼀个(第⼀个)元素交换
3.在剩余的 array[i]–array[n-2](array[i+1]–array[n-1]) 集合中,重复上述步骤,直到集合剩余1个元素
动图:
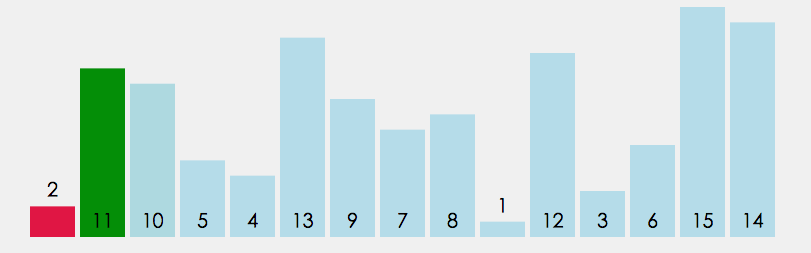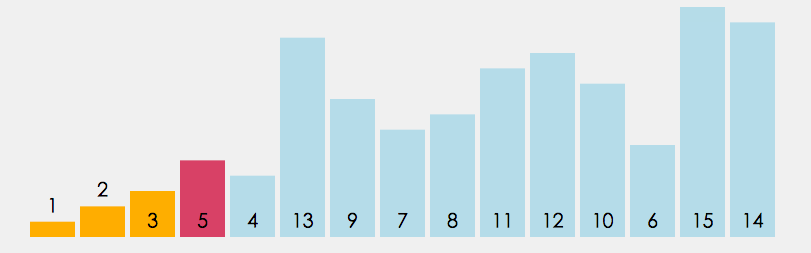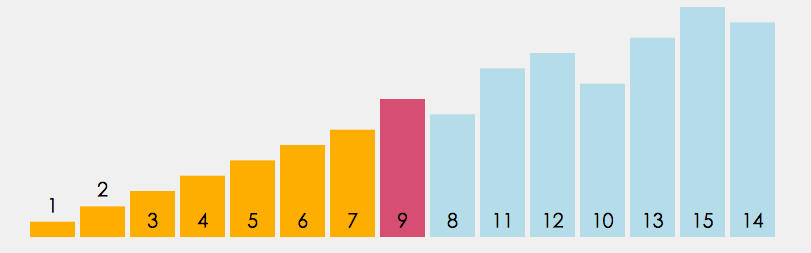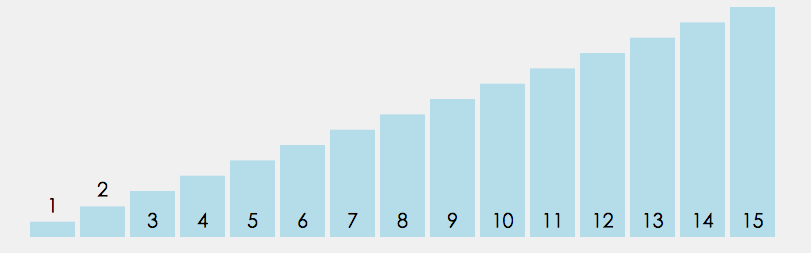
3.2 代码:
void SelectSort(int* arr, int n)
{int begin = 0;int end = n - 1;while (begin < end){int mini = begin;int maxi = begin;for (int i = begin+1; i <= end; i++){if (arr[mini] > arr[i]){mini = i;}if (arr[maxi] < arr[i]){maxi = i;}}//mini begin//maxi end//避免maxi begini都在同一个位置,begin和mini交换之后,maxi数据变成了最小的数据if (maxi == begin){maxi = mini;}Swap(&arr[maxi], &arr[end]);Swap(&arr[mini], &arr[begin]);--end;++begin;}
}1.每次在剩余序列中找最大的和最小的,最大的交换至后面,最小的交换至前面
2.
进入循环,mini找到1,maxi还是在9,此时我们将再将mini和begin交换,maxi与end交换,
end++,begin–跳出循环,排序完成仍然是931,出现了问题。所以需要
if (maxi == begin){maxi = mini;}这样当我们将mini和begin交换完成后,maxi所指向的仍然是最大的数据,将其再与end交换
3.3 复杂度:
1.时间复杂度:O(N^2)
2.空间复杂度:O(1)
四 堆排序:
堆排序是指利⽤堆积树(堆)这种数据结构所设计的⼀种排序算法,它是选择排序的⼀ 种。它是通过堆来进⾏选择数据。需要注意的是排升序要建⼤堆,排降序建⼩堆。
在 【数据结构篇】顺序结构二叉树(堆)的堆排序已经讲过了此方法,这里就不赘述了。
以上就是【数据结构篇】排序1(插入排序与选择排序)的全部内容,欢迎指正~ 🌹🌹🌹
码文不易,还请多多关注支持,这是我持续创作的最大动力!
相关文章:

【数据结构篇】排序1(插入排序与选择排序)
注:本文以排升序为例 常见的排序算法: 目录: 一 直接插入排序: 1.1 基本思想: 1.2 代码: 1.3 复杂度: 二 希尔排序(直接插入排序的优化): 2.1 基本思想…...
《Linux服务与安全管理》| DNS服务器安装和配置
《Linux服务与安全管理》| DNS服务器安装和配置 目录 《Linux服务与安全管理》| DNS服务器安装和配置 第一步:使用dnf命令安装BIND服务 第二步:查看服务器server01的网络配置 第三步:配置全局配置文件 第四步:修改bind的区域…...

【NLP】34. 数据专题:如何打造高质量训练数据集
构建大语言模型的秘密武器:如何打造高质量训练数据集? 在大语言模型(LLM)如 GPT、BERT、T5 爆发式发展的背后,我们常常关注模型架构的演化,却忽视了一个更基础也更关键的问题:训练数据从哪里来…...

Notepad++ 学习(三)使用python插件编写脚本:实现跳转指定标签页(自主研发)
目录 一、先看成果二、安装Python Script插件三、配置Python脚本四、使用脚本跳转标签页方法一:通过菜单运行方法二:设置快捷键(推荐) 五、注意事项六、进阶使用 官网地址: https://notepad-plus-plus.org/Python Scri…...

Stable Diffusion 学习笔记02
模型下载网站: 1,LiblibAI-哩布哩布AI - 中国领先的AI创作平台 2,Civitai: The Home of Open-Source Generative AI 模型的安装: 将下载的sd模型放置在sd1.5的文件内即可,重启客户端可用。 外挂VAE模型:…...

python:pymysql概念、基本操作和注入问题讲解
python:pymysql分享目录 一、概念二、数据准备三、安装pymysql四、pymysql使用(一)使用步骤(二)查询操作(三)增(四)改(五)删 五、关于pymysql注入…...

Scala语言基础与函数式编程详解
Scala语言基础与函数式编程详解 本文系统梳理Scala语言基础、函数式编程核心、集合与迭代器、模式匹配、隐式机制、泛型与Spark实战,并对每个重要专业术语进行简明解释,配合实用记忆口诀与典型代码片段,助你高效学习和应用Scala。 目录 Scal…...

类的加载过程详解
类的加载过程详解 Java类的加载过程分为加载(Loading)、链接(Linking) 和 初始化(Initialization) 三个阶段。其中链接又分为验证(Verification)、准备(Preparation&…...

机器学习-人与机器生数据的区分模型测试 - 模型融合与检验
模型融合 # 先用普通Pipeline训练 from sklearn.pipeline import Pipeline#from sklearn2pmml.pipeline import PMMLPipeline train_pipe Pipeline([(scaler, StandardScaler()),(ensemble, VotingClassifier(estimators[(rf, RandomForestClassifier(n_estimators200, max_de…...

机器学习 day03
文章目录 前言一、特征降维1.特征选择2.主成分分析(PCA) 二、KNN算法三、模型的保存与加载 前言 通过今天的学习,我掌握了机器学习中的特征降维的概念以及用法,KNN算法的基本原理及用法,模型的保存和加载 一、特征降维…...

《社交应用动态表情:RN与Flutter实战解码》
React Native依托于JavaScript和React,为动态表情的实现开辟了一条独特的道路。其核心优势在于对原生模块的便捷调用,这为动态表情的展示和交互提供了强大支持。在社交应用中,当用户点击发送动态表情时,React Native能够迅速调用相…...

嵌入式软件--stm32 DAY 6 USART串口通讯(下)
1.寄存器轮询_收发字符串 通过寄存器轮询方式实现了收发单个字节之后,我们趁热打铁,争上游,进阶到字符串。字符串就是多个字符。很明显可以循环收发单个字节实现。 然后就是接收字符串。如果接受单个字符的函数放在while里,它也可…...

问题处理——在ROS2(humble)+Gazebo+rqt下,无法显示仿真无人机的相机图像
文章目录 前言一、问题展示二、解决方法:1.下载对应版本的PX42.下载对应版本的Gazebo3.启动 总结 前言 在ROS2的环境下,进行无人机仿真的过程中,有时需要调取无人机的相机图像信息,但是使用rqt,却发现相机图像无法显示…...
容器化与云原生)
69、微服务保姆教程(十二)容器化与云原生
容器化与云原生 在微服务架构中,容器化和云原生技术是将应用程序部署到生产环境的核心技术。通过容器化技术,可以将应用程序及其依赖项打包成一个容器镜像,确保在任何环境中都能一致运行。而云原生技术则通过自动化的容器编排系统(如 Kubernetes),实现应用的动态扩展、自…...

朱老师,3518e系列,第六季
第一节:概述。 首先是 将 他写好的 rtsp 源码上传,用于分析。 已经拷贝完。 第二节: h264 编码概念。 编解码 可以用cpu, 也可以用 bsp cpu 编解码的效果不好。做控制比较好。 h264 由 VCL, NAL 组成。 NAL 关心的是 压缩…...

ElasticSearch-集群
本篇文章依据ElasticSearch权威指南进行实操和记录 1,空集群 即不包含任何节点的集群 集群大多数分为两类,主节点和数据节点 主节点 职责:主节点负责管理集群的状态,例如分配分片、添加和删除节点、监控节点故障等。它们不直接…...
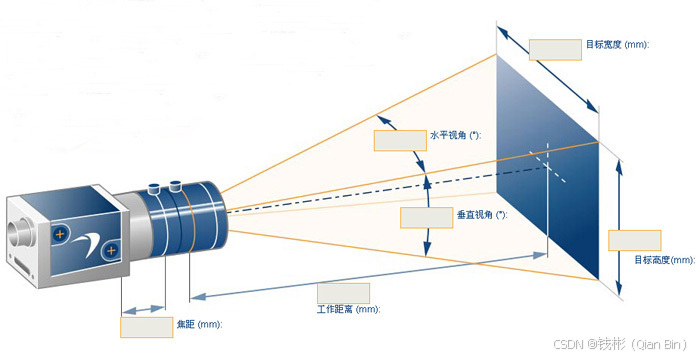
一文掌握工业相机选型计算
目录 一、基本概念 1.1 物方和像方 1.2 工作距离和视场 1.3 放大倍率 1.4 相机芯片尺寸 二、公式计算 三、实例应用 一、基本概念 1.1 物方和像方 在光学领域,物方(Object Space)是与像方(Image Space)相对的…...

记录心态和工作变化
忙中带闲的工作 其实工作挺忙的, 总是在赶各种功能点. 好巧的是iOS那边因为上架的问题耽搁了一些时间, 从而让Android的进度有了很大的调整空间. 更巧的是后端那边因为对客户端的需求不是很熟悉, 加上Android海外这块的业务他也是第一次接触. 所以需要给他留一些时间把各个环节…...

深入理解 TypeScript 中的 unknown 类型:安全处理未知数据的最佳实践
在 TypeScript 的类型体系中,unknown 是一个极具特色的类型。它与 any 看似相似,却在安全性上有着本质差异。本文将从设计理念、核心特性、使用场景及最佳实践等方面深入剖析 unknown,帮助开发者在处理动态数据时既能保持灵活性,又…...

LabVIEW机械振动信号分析与故障诊断
利用 LabVIEW 开发机械振动信号分析与故障诊断系统,融合小波变换、时频分布、高阶统计量(双谱)等先进信号处理技术,实现对齿轮、发动机等机械部件的非平稳非高斯振动信号的特征提取与故障诊断。系统通过虚拟仪器技术将理论算法转化…...
)
Helm配置之为特定Deployment配置特定Docker仓库(覆盖全局配置)
文章目录 Helm配置之为特定Deployment配置特定Docker仓库(覆盖全局配置)需求方法1:使用Helm覆盖值方法2: 在Lens中临时修改Deployment配置步骤 1: 创建 Docker Registry Secret步骤 2: 在 Deployment 中引用 Secret参考资料Helm配置之为特定Deployment配置特定Docker仓库(覆…...

【Spring】Spring中的适配器模式
欢迎来到啾啾的博客🐱。 记录学习点滴。分享工作思考和实用技巧,偶尔也分享一些杂谈💬。 欢迎评论交流,感谢您的阅读😄。 目录 适配器模式Spring MVC的适配器模式 适配器模式 适配器模式(Adapter Pattern&a…...

GO学习指南
GO学习指南 主题一 go语言基础知识讲解 go语言面向对象编程 go语言接口详解 go语言协程 主题二 web基础知识 后续内容请大家持续关注,每月一主题,让各位读者能零基础、零成本学习go语言...

2、ubuntu系统配置OpenSSH | 使用vscode或pycharm远程连接
1、OpenSSH介绍 OpenSSH(Open Secure Shell)是一套基于SSH协议的开源工具,用于在计算机网络中提供安全的加密通信。它被广泛用于远程系统管理、文件传输和网络服务的安全隧道搭建,是保护网络通信免受窃听和攻击的重要工具。 1.1…...

MySQL面试知识点详解
一、MySQL基础架构 1. MySQL逻辑架构 MySQL采用分层架构设计,主要分为: 连接层:处理客户端连接、授权认证等 服务层:包含查询解析、分析、优化、缓存等 引擎层:负责数据存储和提取(InnoDB、MyISAM等&am…...

小白入门:GitHub 远程仓库使用全攻略
一、Git 核心概念 1. 三个工作区域 工作区(Working Directory):实际编辑文件的地方。 暂存区(Staging Area):准备提交的文件集合(使用git add操作)。 本地仓库(Local…...

RPC与SOAP的区别
一.RPC(远程过程调用)和SOAP(简单对象访问协议)均用于实现分布式系统中的远程通信,但两者在设计理念、协议实现及应用场景上存在显著差异。 二.对比 1.设计理念 2.协议规范 3.技术特性 4.典型应用场景 5.总结 三.总结…...

Day11-苍穹外卖(数据统计篇)
前言: 今天写day11的内容,主要讲了四个统计接口的制作。看起来内容较多,其实代码逻辑都是相似的,这里我们过一遍。 今日所学: Apache ECharts营业额统计用户统计订单统计销量排行统计 1. Apache ECharts 1.1 介绍 A…...

Tomcat简述介绍
文章目录 Web服务器Tomcat的作用Tomcat分析目录结构 Web服务器 Web服务器的作用是接收客户端的请求,给客户端作出响应。 知名Java Web服务器 Tomcat(Apache):用来开发学习使用;免费,开源JBoss࿰…...

《从零开始:Spring Cloud Eureka 配置与服务注册全流程》
关于Eureka的学习,主要学习如何搭建Eureka,将order-service和product-service都注册到Eureka。 1.为什么使用Eureka? 我在实现一个查询订单功能时,希望可以根据订单中productId去获取对应商品的详细信息,但是产品服务和订单服…...
