LeetCode 404.左叶子之和的迭代求解:栈结构与父节点定位的深度解析
一、题目解析:左叶子的定义与问题本质
题目描述
LeetCode 404. 左叶子之和要求计算二叉树中所有左叶子节点的值之和。左叶子的定义是:如果一个节点是其父节点的左子节点,并且它本身没有左右子节点,则称为左叶子。
关键要点
- 左叶子的双重条件:
- 必须是父节点的左子节点;
- 自身没有子节点(左右子节点均为空)。
- 问题本质:需要在遍历二叉树的过程中,判断每个节点是否为左叶子,并累加其值。
示例说明
对于二叉树:
3/ \9 20/ \15 7
左叶子为9和15,和为24。
二、迭代解法核心:栈结构与父节点定位逻辑
代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int sumOfLeftLeaves(TreeNode root) {Stack<TreeNode> cur = new Stack<>();if (root == null) {return 0;}int res = 0;TreeNode temp = root;cur.push(root);while (!cur.empty()) {temp = cur.pop();// 检查左子节点是否为左叶子if (temp.left != null && temp.left.left == null && temp.left.right == null) {res += temp.left.val;}// 先压右子节点,再压左子节点(保证左子树先处理)if (temp.right != null) {cur.push(temp.right);}if (temp.left != null) {cur.push(temp.left);}}return res;}
}
核心设计解析:为什么选择栈结构?
1. 栈的特性与深度优先遍历
- 栈的后进先出(LIFO)特性天然适合深度优先遍历(DFS):
- 先压入右子节点,再压入左子节点,确保左子树先于右子树处理;
- 模拟递归调用栈的行为,避免递归可能导致的栈溢出。
2. 栈中存储父节点的必要性
- 左叶子的判断依赖于父节点:
- 必须通过父节点才能确定当前节点是否为左子节点;
- 栈中存储的是父节点,而非当前叶子节点,因此可以直接通过
temp.left判断左子节点是否为叶子。
三、父节点定位左叶子的逻辑深度解析
1. 左叶子的判断条件
if (temp.left != null && temp.left.left == null && temp.left.right == null) {res += temp.left.val;
}
- 条件拆解:
temp.left != null:父节点存在左子节点;temp.left.left == null:左子节点没有左子节点;temp.left.right == null:左子节点没有右子节点。
- 逻辑本质:通过父节点
temp判断其左子节点是否为叶子节点,满足条件则累加值。
2. 栈操作顺序与遍历顺序
if (temp.right != null) {cur.push(temp.right);
}
if (temp.left != null) {cur.push(temp.left);
}
- 入栈顺序:先右子节点,后左子节点;
- 出栈顺序:先左子节点,后右子节点(LIFO);
- 效果:实现深度优先遍历中的先左后右顺序,与递归的前序遍历一致。
3. 栈操作模拟:以示例二叉树为例
示例二叉树:
3/ \9 20/ \15 7
栈操作流程:
-
初始状态:
栈:[3],结果res=0 -
第一次循环:
- 弹出
3,检查左子节点9:
9是3的左子节点,且9没有子节点,累加9,res=9; - 压入右子节点
20,左子节点9(已处理,无需重复处理?不,此处压入的是父节点的子节点);
栈:[20, 9]
- 弹出
-
第二次循环:
- 弹出
9,检查左子节点(9的左子节点为空),无操作; - 压入
9的右子节点(空),左子节点(空);
栈:[20]
- 弹出
-
第三次循环:
- 弹出
20,检查左子节点15:
15是20的左子节点,且15没有子节点,累加15,res=24; - 压入
20的右子节点7,左子节点15;
栈:[7, 15]
- 弹出
-
第四次循环:
- 弹出
15,检查左子节点(空),无操作; - 压入
15的右子节点(空),左子节点(空);
栈:[7]
- 弹出
-
第五次循环:
- 弹出
7,检查左子节点(空),无操作; - 压入
7的右子节点(空),左子节点(空);
栈:空
- 弹出
-
最终结果:
res=24
四、栈结构的核心作用:模拟递归与状态维护
1. 迭代与递归的等价性
| 递归实现 | 迭代栈实现 |
|---|---|
| 系统自动维护调用栈 | 手动维护栈保存节点 |
| 代码简洁但可能栈溢出 | 代码直观且栈深度可控 |
| 隐式保存父节点上下文 | 显式通过父节点判断叶子 |
2. 时间与空间复杂度分析
- 时间复杂度:O(n),每个节点仅访问一次;
- 空间复杂度:O(h),h为树的高度,最坏情况下(链表树)为O(n)。
3. 大厂面试中的考点分析
- 栈的选择:考察对数据结构特性的理解(LIFO适合DFS);
- 父节点定位:考察对左叶子定义的理解(必须通过父节点判断);
- 迭代与递归转换:考察算法实现的灵活性。
五、左叶子判断的常见误区与优化
1. 常见误区
- 误判非左子节点为左叶子:
仅判断节点是否为叶子,忽略“左子节点”的条件。例如:if (node.left == null && node.right == null) { // 错误,未判断是否为左子节点res += node.val; }
2. 优化方向:层序遍历(BFS)实现
public int sumOfLeftLeaves(TreeNode root) {if (root == null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int res = 0;while (!queue.isEmpty()) {TreeNode node = queue.poll();if (node.left != null) {// 左子节点是叶子if (node.left.left == null && node.left.right == null) {res += node.left.val;} else {queue.offer(node.left);}}if (node.right != null) {queue.offer(node.right);}}return res;
}
- 对比:
- 时间复杂度相同(O(n));
- 空间复杂度可能更高(队列平均宽度可能大于栈深度);
- 代码逻辑更直观,适合初学者理解。
3. 极端情况处理
- 单节点树:根节点不是左叶子(无父节点),返回0;
- 只有右子树:所有叶子均非左叶子,返回0;
- 完全左斜树:所有左子节点若为叶子则累加,如树
1->2->3->4,左叶子为2、3、4,和为9。
六、总结:迭代法求解左叶子之和的核心要点
1. 栈结构的双重作用
- 作为遍历容器,实现深度优先搜索;
- 保存父节点,为左叶子判断提供上下文。
2. 左叶子判断的关键
- 必须同时满足“左子节点”和“叶子节点”两个条件;
- 通过父节点的
left指针访问左子节点,判断其是否为叶子。
3. 算法设计的核心思想
- 状态维护:栈中保存的是父节点状态,而非叶子节点;
- 遍历顺序:通过栈的入栈顺序控制遍历顺序,实现深度优先;
- 条件过滤:在遍历过程中实时判断左叶子,避免额外存储。
这种迭代解法充分展示了栈结构在树遍历中的灵活性——通过维护父节点状态,精准定位左叶子节点。理解这种“父节点定位”的思想,对解决类似需要依赖上下文的树节点问题(如求祖父节点值、子树和等)具有重要的借鉴意义。在实际工程中,迭代法因避免递归栈溢出,更适合处理大规模树结构,是大厂面试中需要重点掌握的技能。
相关文章:

LeetCode 404.左叶子之和的迭代求解:栈结构与父节点定位的深度解析
一、题目解析:左叶子的定义与问题本质 题目描述 LeetCode 404. 左叶子之和要求计算二叉树中所有左叶子节点的值之和。左叶子的定义是:如果一个节点是其父节点的左子节点,并且它本身没有左右子节点,则称为左叶子。 关键要点 左…...

Unity-编辑器扩展
之前我们关于Unity的讨论都是针对于Unity底层的内容或者是代码层面的东西,这一次我们来专门研究Unity可视化的编辑器,在已有的基础上做一些扩展。 基本功能 首先我们来认识三个文件夹: Editor,Gizmos,Editor Defaul…...

【自用-python】生成准心居中exe程序,防止云电脑操作时候鼠标偏移
封装exe:: altf12是终端---我理解的就是最初始python的运行台 看where python(Windows的)看是在那个路径 再确保之前pip安装了pyinstaller 然后pyinstaller --onefile --noconsole --name 输出exe的文件名称 你的py文件名称.py…...

Lucide:一款精美的开源矢量图标库,前端图标新选择
名人说:博观而约取,厚积而薄发。——苏轼《稼说送张琥》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、前言:为何选择 Lucide?二、Lucide 是什么?1.…...

在Rocky Linux 8.10上安装Nginx
如果没有配置操作系统安装源,并且不连接网络,先配置安装源。 sudo dnf install nginx sudo systemctl enable nginx sudo systemctl start nginx systemctl status nginx curl http://ip [rootrocky810 work]# sudo dnf install nginx Last metadata …...

Mac如何允许安装任何来源软件?
打开系统偏好设置-安全性与隐私,点击右下角的解锁按钮,选择允许从任何来源。 如果没有这一选项,请到打开终端,输入命令行:sudo spctl --master-disable, 输入命令后回车,输入电脑的开机密码后回车。 返回“…...

YOLO学习笔记 | YOLO11对象检测,实例分割,姿态评估的TensorRT部署c++
以下是YOLOv11在TensorRT上部署的步骤指南,涵盖对象检测、实例分割和姿态评估: 1. 模型导出与转换 1.1 导出ONNX模型 import torch from models.experimental import attempt_loadmodel = attempt_load(yolov11s.pt, fuse=True) model.eval...

2025最新版Visual Studio Code for Mac安装使用指南
2025最新版Visual Studio Code for Mac安装使用指南 Installation and Application Guide to The Latest Version of Visual Studio Code in 2025 By JacksonML 1. 什么是Visual Studio Code? Visual Studio Code,通常被称为 VS Code,是由…...

机器学习第二十三讲:CNN → 用放大镜局部观察图片特征层层传递
机器学习第二十三讲:CNN → 用放大镜局部观察图片特征层层传递 资料取自《零基础学机器学习》。 查看总目录:学习大纲 关于DeepSeek本地部署指南可以看下我之前写的文章:DeepSeek R1本地与线上满血版部署:超详细手把手指南 CNN详…...

【嵙大o】C++作业合集
参考: C swap(交换)函数 指针/引用/C自带-CSDN博客 Problem IDTitleCPP指针CPP引用1107 Problem A编写函数:Swap (I) (Append Code)1158 Problem B整型数据的输出格式1163 Problem C时间:24小时制转12小时制1205…...

《算法笔记》11.8小节——动态规划专题->总结 问题 B: 拦截导弹
题目描述 某国为了防御敌国的导弹袭击,开发出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭,…...

Flink 核心概念解析:流数据、并行处理与状态
一、流数据(Stream Data) 1. 有界流(Bounded Stream) 定义:有明确起始和结束时间的数据集合,数据量固定,处理逻辑通常是一次性计算所有数据。 典型场景: 历史交易数据统计…...

C++23 范围迭代器作为非范围算法的输入 (P2408R5)
文章目录 一、引言二、C23及范围迭代器的背景知识2.1 C23概述2.2 范围迭代器的概念 三、P2408R5提案的内容3.1 提案背景3.2 提案内容 四、范围迭代器作为非范围算法输入的优势4.1 代码简洁性4.2 提高开发效率4.3 更好的兼容性 五、具体的代码示例5.1 使用范围迭代器进行并行计算…...

PHP-FPM 调优配置建议
1、动态模式 pm dynamic; 最大子进程数(根据服务器内存调整) pm.max_children 100 //每个PHP-FPM进程大约占用30-50MB内存(ThinkPHP框架本身有一定内存开销)安全值:8GB内存 / 50MB ≈ 160,保守设置为100 ; 启动时创建的进程数&…...

2025.05.20【Treemap】树图数据可视化技巧
Multi-level treemap How to build a treemap with group and subgroups. Customization Customize treemap labels, borders, color palette and more 文章目录 Multi-level treemapCustomization Treemap 数据可视化技巧什么是 TreemapTreemap 的应用场景如何在 R 中绘制 T…...

Elasticsearch 写入性能优化有哪些常见手段?
Elasticsearch 写入性能优化常见手段主要有以下 10 个方向,建议根据具体业务场景组合使用: 批量写入优化 使用_bulk API 批量提交文档建议每批次 5-15MB 数据量并发执行多个批量请求 索引配置调优 PUT /my_index {"settings": {"inde…...

CICD编译时遇到npm error code EINTEGRITY的问题
场景 CICD编译时抛出npm error code EINTEGRITY的错误 npm error code EINTEGRITY npm error sha512-PlhdFcillOINfeV7Ni6oF1TAEayyZBoZ8bcshTHqOYJYlrqzRK5hagpagky5o4HfCzzd1TRkXPMFq6cKk9rGmA integrity checksum failed when using sha512: wanted sha512-PlhdFcillOINfeV…...

深入了解Springboot框架的启动流程
目录 1、介绍 2、执行流程 1、运行run方法 2、初始化SpringApplication对象 1、确定容器类型 3、加载所有的初始化器 4、加载Spring上下文监听器 5、设置程序运行的主类 3、进入run方法 1、开启计时器 2、Headless模式配置 3、获取并启用监听器 4、准备环境 1、设…...

DataWhale llm universe
搭建向量知识库 向量以及向量知识库 向量词与向量 词向量:是一种以单词为单位的将每个单词转化为实数向量的技术,这些实数可以被计算机更好的理解,如果是相近的理念或者相关的对象在向量空间中距离很近 词向量实际上将单词转化为固定的静态…...

LLaMA-Factory微调LLM-Research/Llama-3.2-3B-Instruct模型
1、GPU环境 nvidia-smi 2、pyhton环境安装 git clone https://github.com/hiyouga/LLaMA-Factory.git conda create -n llama_factory python3.10 conda activate llama_factory cd LLaMA-Factory pip install -e .[torch,metrics] 3、微调模型下载(LLM-Research/…...

DB-MongoDB-00002--Workload Generator for MongoDB
## DB-MongoDB-00002–Workload Generator for MongoDB 1、介绍 Workload Generator for MongoDB was designed to help MongoDB users effortlessly generate data and simulate workloads for both sharded and non-sharded clusters. The generated workloads include s…...

3.8.1 利用RDD实现词频统计
在本次实战中,我们通过Spark的RDD实现了词频统计功能。首先,准备了包含单词的文件并上传至HDFS。接着,采用交互式方式逐步完成词频统计,包括创建RDD、单词拆分、映射为二元组、按键归约以及排序等操作。此外,还通过创建…...

Spring Ioc和Aop,Aop的原理和实现案例,JoinPoint,@Aspect,@Before,@AfterReturning
DAY25.2 Java核心基础 Spring两大核心:Ioc和Aop IOC Ioc容器:装载bean的容器,自动创建bean 三种方式: 1、基于xml配置:通过在xml里面配置bean,然后通过反射机制创建bean,存入进Ioc容器中 …...
[解决conda创建新的虚拟环境没用python的问题]
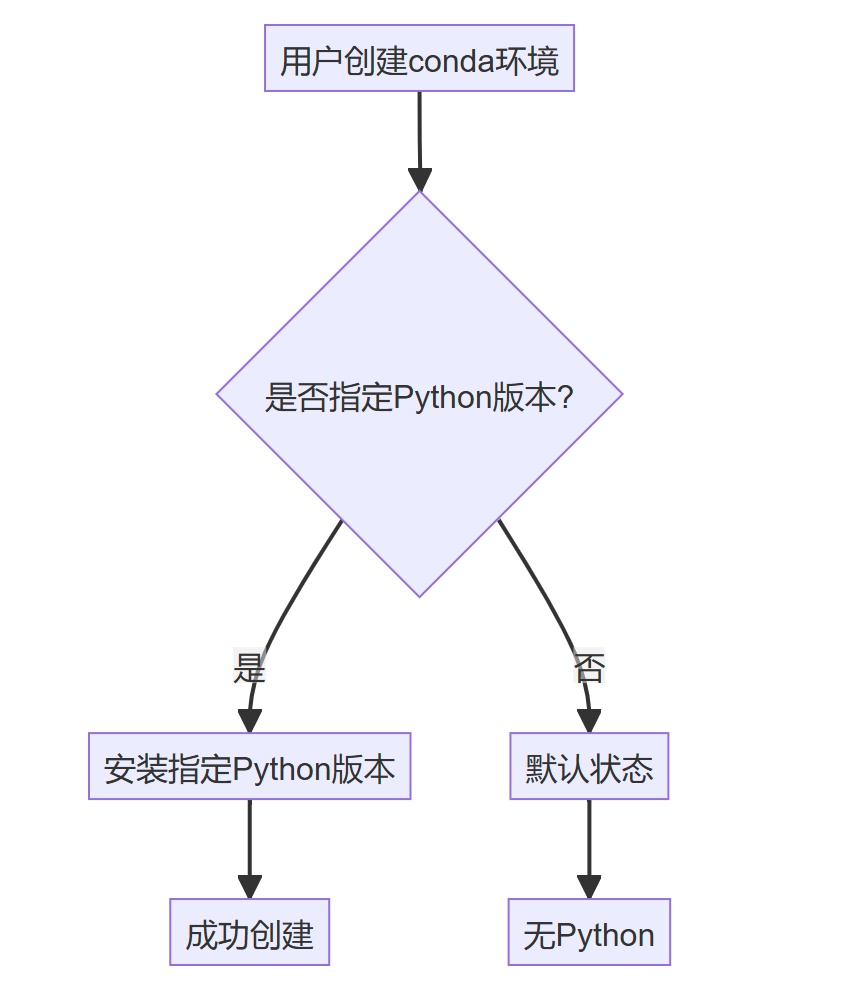
问题复现 使用conda create -n env的时候,在对应的虚拟环境的文件里面找不到对应的python文件 为什么 首先,我们来看一下创建环境时的触发链路: 这表明当前环境中找不到Python可执行文件。 解决方法 所以很明显,我们需要指定…...

【优秀三方库研读】在 quill 开源库 LogMarcos.h 中知识点汇总及讲解
以下是LogMarcos.h中的主要知识点汇总及详细讲解: 大纲目录 编译时日志级别过滤预处理宏与条件编译可变参数处理技巧格式化字符串生成日志宏的分发机制线程本地存储(TLS)零成本抽象设计动态日志级别支持结构化日志标签日志频率限制机制1. 编译时日志级别过滤 核心宏:QUILL…...
openjdk17 c++源码垃圾回收之安全点阻塞状态线程在安全点同步中无需调用block函数的详细流程解析)
jvm安全点(五)openjdk17 c++源码垃圾回收之安全点阻塞状态线程在安全点同步中无需调用block函数的详细流程解析
关于阻塞状态线程在安全点同步中无需调用block函数的详细流程解析: 1. 安全点同步入口:SafepointSynchronize::begin() VM线程调用此函数启动安全点,核心步骤如下: 获取线程锁(Threads_lock):防…...

C++ 中的 **常变量** 与 **宏变量** 比较
🔍 C 中的 常变量 与 宏变量 比较 C 中定义不可修改值的方式主要有两种:常变量(const/constexpr) 和 宏变量(#define)。它们在机制、类型安全性、作用域和调试支持方面存在显著差异。 ✅ 1. 常变量&#x…...

【C++】控制台小游戏
移动:W向上,S上下,A向左,D向右 程序代码: #include <iostream> #include <conio.h> #include <windows.h> using namespace std;bool gameOver; const int width 20; const int height 17; int …...

配合本专栏前端文章对应的后端文章——从模拟到展示:一步步搭建传感器数据交互系统
对应文章:进一步完善前端框架搭建及vue-konva依赖的使用(Vscode)-CSDN博客 目录 一、后端开发 1.模拟传感器数据 2.前端页面呈现数据后端互通 2.1更新模拟传感器数据程序(多次请求) 2.2🧩 功能目标 …...

React中常用的钩子函数:
一. 基础钩子 (1)useState 用于在函数组件中添加局部状态。useState可以传递一个参数,做为状态的初始值,返回一个数组,数组的第一个元素是返回的状态变量,第二个是修改状态变量的函数。 const [state, setState] useState(ini…...
