Java详解LeetCode 热题 100(20):LeetCode 48. 旋转图像(Rotate Image)详解
文章目录
- 1. 题目描述
- 2. 理解题目
- 3. 解法一:转置 + 翻转
- 3.1 思路
- 3.2 Java代码实现
- 3.3 代码详解
- 3.4 复杂度分析
- 3.5 适用场景
- 4. 解法二:四点旋转法
- 4.1 思路
- 4.2 Java代码实现
- 4.3 代码详解
- 4.4 复杂度分析
- 4.5 适用场景
- 5. 详细步骤分析与示例跟踪
- 5.1 解法一:3×3矩阵示例
- 5.2 解法二:3×3矩阵示例
- 5.3 4×4矩阵示例
- 5.4 特殊情况:奇数大小的矩阵
- 5.5 动态示意图
- 6. 常见错误与优化
- 6.1 常见错误
- 6.2 性能优化
- 7. 扩展题目与应用
- 7.1 相关矩阵变换问题
- 7.2 旋转相关的其他题目
- 8. 实际应用场景
- 9. 完整的 Java 解决方案
- 10. 总结与技巧
- 10.1 解题要点
- 10.2 学习收获
- 10.3 面试技巧
- 10.4 考察重点
- 11. 旋转矩阵的数学原理
- 11.1 线性代数视角
- 11.2 四点旋转的数学关系
- 11.3 转置和翻转的组合等价性
1. 题目描述
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
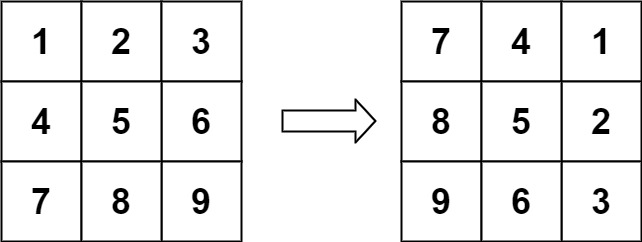
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
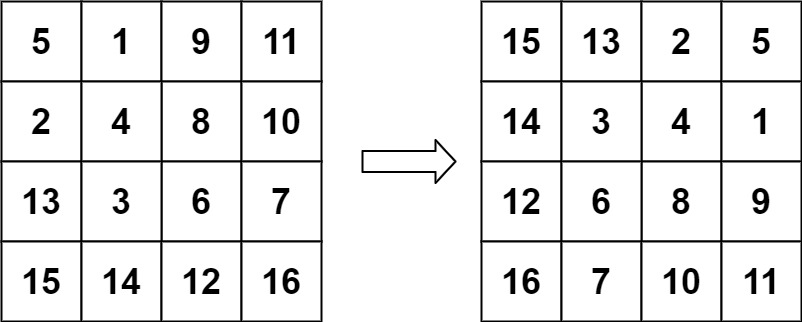
示例 2:
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
- n == matrix.length == matrix[i].length
- 1 <= n <= 20
- -1000 <= matrix[i][j] <= 1000
2. 理解题目
这道题要求我们将一个 n×n 的矩阵顺时针旋转 90 度,并且必须在原地修改,不能使用额外的矩阵。理解这个问题的关键在于:
- 矩阵是正方形的:这一点很重要,因为只有正方形矩阵才能原地旋转 90 度。
- 顺时针旋转 90 度:图像顺时针旋转 90 度后,原矩阵中的元素位置会发生变化。具体来说:
- 第一行元素会变成最后一列(从上到下)
- 第二行元素会变成倒数第二列(从上到下)
- 依此类推…
- 原地修改:我们不能使用额外的矩阵来存储旋转后的结果,必须直接修改输入矩阵。
如果用坐标来表示,对于一个位于 (row, col) 的元素,旋转 90 度后,它的新位置应该是 (col, n-1-row)。这种变换会形成一个循环:
(row, col) → (col, n-1-row) → (n-1-row, n-1-col) → (n-1-col, row) → (row, col)
这一循环关系是解决这个问题的关键。我们需要在不使用额外空间的情况下,利用这个关系完成矩阵的旋转。
3. 解法一:转置 + 翻转
3.1 思路
将矩阵顺时针旋转 90 度可以分解为两个简单的操作:
- 先沿对角线转置矩阵(即交换 matrix[i][j] 和 matrix[j][i])
- 再将每一行左右翻转(即交换 matrix[i][j] 和 matrix[i][n-1-j])
这种解法的优势在于操作简单,易于理解和实现。
示意图:
原始矩阵: 转置后: 左右翻转后:
1 2 3 1 4 7 7 4 1
4 5 6 -> 2 5 8 -> 8 5 2
7 8 9 3 6 9 9 6 3
3.2 Java代码实现
class Solution {public void rotate(int[][] matrix) {int n = matrix.length;// 沿对角线转置矩阵for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}// 左右翻转每一行for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) {// 交换matrix[i][j]和matrix[i][n-1-j]int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;}}}
}
3.3 代码详解
让我们详细解释这个解法的每个部分:
int n = matrix.length;
- 获取矩阵的大小,由于是正方形矩阵,所以行数和列数相等,都是n。
// 沿对角线转置矩阵
for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}
}
- 这段代码实现了矩阵的转置操作,将矩阵沿着主对角线(从左上到右下)进行翻转。
- 外层循环
i遍历每一行,内层循环j从i开始遍历,这样只处理对角线上和对角线右上方的元素。 - 通过交换
matrix[i][j]和matrix[j][i],我们实现了转置操作。 - 注意内层循环
j是从i开始的,这样可以避免重复交换。例如,当我们交换了matrix[1][2]和matrix[2][1]后,就不需要再交换matrix[2][1]和matrix[1][2]了。
// 左右翻转每一行
for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) {// 交换matrix[i][j]和matrix[i][n-1-j]int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;}
}
- 这段代码实现了将每一行左右翻转的操作。
- 外层循环
i遍历每一行,内层循环j只需要遍历到每行的一半位置。 - 通过交换
matrix[i][j]和matrix[i][n-1-j],我们实现了左右翻转。 - 内层循环只到
n/2是因为,当我们交换了左半部分和右半部分后,整行就已经完成了翻转,无需重复交换。
通过这两步操作,我们实现了矩阵的顺时针旋转 90 度,并且是在原矩阵上直接修改的,符合题目要求。
3.4 复杂度分析
- 时间复杂度: O(n²),其中 n 是矩阵的边长。我们需要访问矩阵中的每个元素至少一次。
- 空间复杂度: O(1),我们只使用了常数额外空间。
3.5 适用场景
这种解法简单直观,易于理解和实现,适用于所有的正方形矩阵旋转情况。特别是当你需要解释矩阵旋转的原理时,这种分解为转置和翻转的方法非常有教学价值。
4. 解法二:四点旋转法
4.1 思路
另一种思路是直接模拟旋转过程,每次旋转矩阵中的4个点。我们可以从外层开始,一层一层向内处理。对于每个位置(i,j),可以找到旋转后对应的其他三个位置,然后一次性完成这四个位置的旋转。
具体来说,对于位置(i,j),旋转90度后的新位置是(j,n-1-i)。我们可以找出四个互相旋转的位置:
- (i,j) -> (j,n-1-i) -> (n-1-i,n-1-j) -> (n-1-j,i) -> (i,j)
然后,我们只需要一个临时变量就可以完成这四个位置的值旋转。
示意图:
(0,0) -> (0,2) -> (2,2) -> (2,0) -> (0,0)
(0,1) -> (1,2) -> (2,1) -> (1,0) -> (0,1)
4.2 Java代码实现
class Solution {public void rotate(int[][] matrix) {int n = matrix.length;// 从外层向内层处理,一共有 n/2 层for (int layer = 0; layer < n / 2; layer++) {// 每层需要处理的元素个数int first = layer;int last = n - 1 - layer;// 对当前层的每个元素进行旋转for (int i = first; i < last; i++) {// 存储上边的元素int temp = matrix[first][i];// 左边 -> 上边matrix[first][i] = matrix[n - 1 - i][first];// 下边 -> 左边matrix[n - 1 - i][first] = matrix[last][n - 1 - i];// 右边 -> 下边matrix[last][n - 1 - i] = matrix[i][last];// 上边(temp) -> 右边matrix[i][last] = temp;}}}
}
4.3 代码详解
让我们详细解释这个解法的每个部分:
// 从外层向内层处理,一共有 n/2 层
for (int layer = 0; layer < n / 2; layer++) {// 每层需要处理的元素个数int first = layer;int last = n - 1 - layer;// 对当前层的每个元素进行旋转for (int i = first; i < last; i++) {// 存储上边的元素int temp = matrix[first][i];// 左边 -> 上边matrix[first][i] = matrix[n - 1 - i][first];// 下边 -> 左边matrix[n - 1 - i][first] = matrix[last][n - 1 - i];// 右边 -> 下边matrix[last][n - 1 - i] = matrix[i][last];// 上边(temp) -> 右边matrix[i][last] = temp;}
}
- 外层循环控制处理的层数,从最外层(layer=0)开始,一直到最内层。
- 对于一个n×n的矩阵,总共有n/2层(如果n是奇数,最中心的元素不需要旋转)。
first表示当前层的起始位置,last表示当前层的结束位置。
// 对当前层的每个元素进行旋转
for (int i = first; i < last; i++) {// ...
}
- 内层循环处理当前层的每个元素。
- 对于每个位置(first,i),我们找出旋转后对应的其他三个位置,然后一次性完成旋转。
// 存储上边的元素
int temp = matrix[first][i];// 左边 -> 上边
matrix[first][i] = matrix[n - 1 - i][first];// 下边 -> 左边
matrix[n - 1 - i][first] = matrix[last][n - 1 - i];// 右边 -> 下边
matrix[last][n - 1 - i] = matrix[i][last];// 上边(temp) -> 右边
matrix[i][last] = temp;
- 这四行代码完成了四个位置的旋转。
- 首先,我们保存上边的元素到
temp。 - 然后,将左边的元素移动到上边,下边的元素移动到左边,右边的元素移动到下边。
- 最后,将保存在
temp中的原上边元素移动到右边。
通过这种方式,我们实现了矩阵的顺时针旋转90度,并且是在原矩阵上直接修改的。
4.4 复杂度分析
- 时间复杂度: O(n²),其中 n 是矩阵的边长。虽然我们使用了两层循环,但并没有访问矩阵中的所有元素,只访问了大约四分之一的元素。然而,在渐近意义上,这仍然是O(n²)。
- 空间复杂度: O(1),我们只使用了常数额外空间(一个临时变量)。
4.5 适用场景
四点旋转法更符合矩阵旋转的直接定义,不需要理解转置和翻转的组合。这种方法适用于需要直接模拟旋转过程的场景,例如:
- 在图像处理中,当需要理解或可视化旋转过程时
- 当问题要求追踪每个元素在旋转过程中的确切路径时
- 在教学中解释矩阵旋转的具体流程时
5. 详细步骤分析与示例跟踪
让我们通过具体的例子详细跟踪每种解法的执行过程,以深入理解算法的工作原理。
5.1 解法一:3×3矩阵示例
以示例1中的3×3矩阵为例:
1 2 3
4 5 6
7 8 9
第一步:转置矩阵
-
初始状态:
1 2 3 4 5 6 7 8 9 -
转置矩阵意味着交换对角线上方的元素,即交换(i,j)和(j,i):
- 交换(0,1)和(1,0):将2和4交换
1 4 3 2 5 6 7 8 9- 交换(0,2)和(2,0):将3和7交换
1 4 7 2 5 6 3 8 9- 交换(1,2)和(2,1):将6和8交换
1 4 7 2 5 8 3 6 9 -
转置完成后的矩阵:
1 4 7 2 5 8 3 6 9
第二步:左右翻转每一行
-
初始状态(转置后的矩阵):
1 4 7 2 5 8 3 6 9 -
对每一行进行左右翻转:
- 第一行:交换1和7
7 4 1 2 5 8 3 6 9- 第二行:交换2和8
7 4 1 8 5 2 3 6 9- 第三行:交换3和9
7 4 1 8 5 2 9 6 3 -
最终结果:
7 4 1 8 5 2 9 6 3
这就是顺时针旋转90度后的矩阵。
5.2 解法二:3×3矩阵示例
以同样的3×3矩阵为例:
1 2 3
4 5 6
7 8 9
使用四点旋转法:
-
初始状态:
1 2 3 4 5 6 7 8 9 -
分析层数:
- 3×3矩阵只有1层(最外层)
- first = 0, last = 2
-
对第0层的每个元素进行旋转(从first到last-1):
-
处理元素(0,0):
- 保存temp = matrix[0][0] = 1
- 左边到上边:matrix[0][0] = matrix[2][0] = 7
- 下边到左边:matrix[2][0] = matrix[2][2] = 9
- 右边到下边:matrix[2][2] = matrix[0][2] = 3
- 上边到右边:matrix[0][2] = temp = 1
7 2 1 4 5 6 9 8 3 -
处理元素(0,1):
- 保存temp = matrix[0][1] = 2
- 左边到上边:matrix[0][1] = matrix[1][0] = 4
- 下边到左边:matrix[1][0] = matrix[2][1] = 8
- 右边到下边:matrix[2][1] = matrix[1][2] = 6
- 上边到右边:matrix[1][2] = temp = 2
7 4 1 8 5 2 9 6 3
-
-
最终结果:
7 4 1 8 5 2 9 6 3
5.3 4×4矩阵示例
以示例2中的4×4矩阵为例:
5 1 9 112 4 8 10
13 3 6 7
15 14 12 16
使用解法一(转置+翻转):
-
转置矩阵后:
5 2 13 151 4 3 149 8 6 12 11 10 7 16 -
左右翻转每一行后:
15 13 2 5 14 3 4 1 12 6 8 9 16 7 10 11
使用解法二(四点旋转法):
对于4×4矩阵,我们需要处理2层:最外层和次外层。
-
处理最外层(layer=0):
- first = 0, last = 3
- 依次旋转(0,0), (0,1), (0,2)对应的四个点
- 旋转后变为:
15 13 2 5 14 4 8 1 12 3 6 9 16 10 7 11 -
处理次外层(layer=1):
- first = 1, last = 2
- 旋转(1,1)对应的四个点
- 旋转后变为:
15 13 2 5 14 3 4 1 12 6 8 9 16 7 10 11
5.4 特殊情况:奇数大小的矩阵
对于奇数大小的矩阵(例如5×5),中心点不需要旋转。
例如5×5矩阵:
1 2 3 4 56 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
- 解法一(转置+翻转)不受影响,照常操作即可。
- 解法二(四点旋转法)需要处理2层(最外层和次外层),中心点(2,2)不需要处理。
5.5 动态示意图
下面是旋转过程的动态示意图:
解法一:转置+翻转
原始矩阵: -> 转置后: -> 左右翻转后:
1 2 3 1 4 7 7 4 1
4 5 6 -> 2 5 8 -> 8 5 2
7 8 9 3 6 9 9 6 3
解法二:四点旋转
旋转(0,0)位置的四个点: 旋转(0,1)位置的四个点:
1 2 3 7 2 1
4 5 6 -> 4 5 6 ->
7 8 9 9 8 3最终结果:
7 4 1
8 5 2
9 6 3
6. 常见错误与优化
6.1 常见错误
-
转置矩阵时的索引错误:
在解法一中,转置矩阵时常见的错误是内层循环的起始点选择。// 错误写法:会导致重复交换 for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) { // 错误:应为j = iint temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;} }// 正确写法:避免重复交换 for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) { // 从i开始,避免重复交换int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;} } -
左右翻转时的范围错误:
翻转每行时,只需要遍历到行的一半位置。// 错误写法:会导致重复交换,使结果不变 for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) { // 错误:应为j < n/2int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;} }// 正确写法:只遍历到一半 for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) { // 只需交换一半int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;} } -
四点旋转法的下标计算错误:
在解法二中,容易在计算旋转后的四个点位置时出错。// 错误写法:下标计算错误 int temp = matrix[first][i]; matrix[first][i] = matrix[i][first]; // 错误:应为matrix[n-1-i][first] matrix[i][first] = matrix[last][i]; // 错误 matrix[last][i] = matrix[i][last]; // 错误 matrix[i][last] = temp;// 正确写法:正确计算旋转后的位置 int temp = matrix[first][i]; matrix[first][i] = matrix[n - 1 - i][first]; matrix[n - 1 - i][first] = matrix[last][n - 1 - i]; matrix[last][n - 1 - i] = matrix[i][last]; matrix[i][last] = temp; -
忽略特殊情况:
对于n=1的情况(单个元素的矩阵),旋转不会改变矩阵。需要检查这种特殊情况,避免不必要的操作。// 添加边界检查 if (matrix == null || matrix.length <= 1) {return; // 单个元素或空矩阵不需旋转 }
6.2 性能优化
-
减少交换次数:
在解法一中,转置矩阵时只需要交换对角线上方的元素,而不是整个矩阵。这已经在正确实现中体现。 -
原地操作优化:
两种解法都已经是原地操作,空间复杂度为O(1),已经是最优的。 -
循环优化:
在解法二中,可以考虑将四个点的旋转合并为一个表达式,减少临时变量的使用,但可能会降低代码的可读性。// 优化:直接四点交换 for (int layer = 0; layer < n / 2; layer++) {int first = layer;int last = n - 1 - layer;for (int i = first; i < last; i++) {int offset = i - first;int top = matrix[first][i];// 四点直接交换matrix[first][i] = matrix[last - offset][first];matrix[last - offset][first] = matrix[last][last - offset];matrix[last][last - offset] = matrix[i][last];matrix[i][last] = top;} } -
利用矩阵特性:
对于某些特殊矩阵(如对角矩阵、对称矩阵等),可以根据其特性简化旋转过程,但在通用解法中不适用。
7. 扩展题目与应用
7.1 相关矩阵变换问题
-
LeetCode 867. 转置矩阵:
给你一个二维整数数组 matrix,返回 matrix 的转置矩阵。矩阵的转置是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引。这与我们解法一的第一步相似。 -
LeetCode 832. 翻转图像:
给你一个二维整数数组 A,每一个子数组中的元素代表一个像素点。将每一个子数组水平翻转,并将每个元素取反。这与解法一的第二步有相似之处。 -
LeetCode 73. 矩阵置零:
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。这也是一个要求原地修改矩阵的问题。
7.2 旋转相关的其他题目
-
LeetCode 189. 轮转数组:
给你一个数组,将数组中的元素向右轮转 k 个位置。这与矩阵旋转有相似的思想。 -
LeetCode 54. 螺旋矩阵:
按照顺时针螺旋顺序,返回矩阵中的所有元素。这与矩阵的旋转有一定的关联。 -
LeetCode 59. 螺旋矩阵 II:
生成一个按照顺时针螺旋填充的n×n矩阵。
8. 实际应用场景
矩阵旋转在实际应用中有许多用途,特别是在图像处理和计算机图形学领域:
-
图像处理:
- 数字图像可以表示为像素值矩阵,旋转图像就是旋转这个矩阵
- 在图像编辑软件(如Photoshop)中,图像旋转是基本功能
- 在OCR(光学字符识别)技术中,需要对倾斜的文档图像进行旋转校正
-
计算机图形学:
- 3D渲染中,物体的旋转可以通过旋转矩阵实现
- 游戏开发中,角色动画和场景变换常需要矩阵旋转
-
机器人技术:
- 机器人运动控制中,物体的旋转和移动需要矩阵变换
- 在路径规划算法中,需要考虑物体的旋转状态
-
科学可视化:
- 在数据可视化中,旋转视图可以从不同角度展示数据
- 医学影像(如CT、MRI)处理中,需要对三维图像进行重构和旋转
-
人工智能:
- 在计算机视觉中,图像旋转是数据增强的常用方法
- 在模式识别中,旋转不变性是重要的特性
-
地理信息系统:
- 在GIS中,地图的旋转和投影需要矩阵变换
- 卫星图像处理中需要考虑地球自转带来的旋转
-
游戏开发:
- 棋盘游戏(如俄罗斯方块、连连看等)中,图形元素的旋转
- 物理引擎中,碰撞检测和物体旋转的计算
这个旋转图像的算法提供了一种高效、原地的方法来执行90度旋转,适用于各种需要矩阵旋转的实际应用场景。
9. 完整的 Java 解决方案
以下是结合了各种优化和最佳实践的完整解决方案:
class Solution {/*** 旋转图像 - 转置+翻转法* 时间复杂度: O(n²)* 空间复杂度: O(1)*/public void rotate(int[][] matrix) {// 处理边界情况if (matrix == null || matrix.length <= 1) {return;}int n = matrix.length;// 沿对角线转置矩阵for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}// 左右翻转每一行for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) {// 交换matrix[i][j]和matrix[i][n-1-j]int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;}}}/*** 备选方案 - 四点旋转法* 时间复杂度: O(n²)* 空间复杂度: O(1)*/public void rotateAlternative(int[][] matrix) {// 处理边界情况if (matrix == null || matrix.length <= 1) {return;}int n = matrix.length;// 从外层向内层处理,一共有 n/2 层for (int layer = 0; layer < n / 2; layer++) {int first = layer;int last = n - 1 - layer;// 对当前层的每个元素进行旋转for (int i = first; i < last; i++) {int offset = i - first;// 存储上边的元素int temp = matrix[first][i];// 左边 -> 上边matrix[first][i] = matrix[n - 1 - i][first];// 下边 -> 左边matrix[n - 1 - i][first] = matrix[last][n - 1 - i];// 右边 -> 下边matrix[last][n - 1 - i] = matrix[i][last];// 上边 -> 右边matrix[i][last] = temp;}}}
}
这个完整的解决方案提供了两种实现方法:
rotate方法实现了转置+翻转的解法,代码简洁明了rotateAlternative方法实现了四点旋转法,更直观地模拟了旋转过程
两种方法都处理了边界情况,并使用了最优的实现方式。在实际应用中,可以根据需要选择任意一种方法。
10. 总结与技巧
10.1 解题要点
-
理解矩阵旋转的几何意义:
- 顺时针旋转90度使第一行变成最后一列,第二行变成倒数第二列,依此类推
- 了解点(i,j)旋转后的新位置是(j,n-1-i)
-
寻找数学规律:
- 转置+翻转的组合等同于90度旋转
- 四个点之间存在循环旋转关系
-
原地操作技巧:
- 利用临时变量完成元素交换
- 避免重复操作,如在转置矩阵时只处理对角线上方的元素
-
分层处理思想:
- 在四点旋转法中,从外到内一层一层处理矩阵
- 对于每一层,按照相同的模式旋转四个对应点
-
边界条件处理:
- 注意空矩阵和单元素矩阵的特殊情况
- 对于奇数大小的矩阵,中心点不需要旋转
10.2 学习收获
通过学习旋转图像问题,你可以掌握:
- 矩阵操作的基本技巧
- 空间几何变换的数学关系
- 原地算法的设计思想
- 分解复杂问题为简单操作的能力
10.3 面试技巧
如果在面试中遇到此类问题:
- 先分析问题,理解旋转的定义和要求
- 从最直接的解法开始,如四点旋转法,这样易于展示思考过程
- 可以提出转置+翻转的优化方法,展示数学思维能力
- 讨论边界情况和可能的优化
- 提及该问题在实际应用中的意义,如图像处理
特别注意,这个问题容易出错的地方是索引计算,因此在面试中实现时要格外小心。
10.4 考察重点
这道题主要考察:
- 矩阵操作能力
- 空间想象力
- 原地算法设计
- 边界条件处理
- 代码实现的细节把控
11. 旋转矩阵的数学原理
为了更深入地理解矩阵旋转,我们可以从数学角度分析旋转变换的原理。
11.1 线性代数视角
在线性代数中,二维平面上的旋转可以通过旋转矩阵表示。顺时针旋转90度的旋转矩阵为:
R = [ 0 1][-1 0]
对于点(x,y),旋转后的新坐标(x’,y’)可以通过矩阵乘法计算:
[x'] [ 0 1] [x]
[y'] = [-1 0] [y]
展开得:
x' = y
y' = -x
将这个公式应用到矩阵索引上,假设点(i,j)在旋转后变为(i’,j’):
i' = j
j' = n-1-i
这正是解法一中的转置(i’=j, j’=i)和左右翻转(j’=n-1-j’)所实现的效果。
11.2 四点旋转的数学关系
在解法二中,我们旋转了四个位置的点。这四个位置形成了一个循环:
(i,j) -> (j,n-1-i) -> (n-1-i,n-1-j) -> (n-1-j,i) -> (i,j)
这种循环关系可以通过连续应用旋转变换得到:
- 点(i,j)旋转90度后变为(j,n-1-i)
- 再旋转90度变为(n-1-i,n-1-j)
- 再旋转90度变为(n-1-j,i)
- 再旋转90度回到原点(i,j)
这个循环恰好是360度的完整旋转,因此四个点形成了一个封闭的变换循环。
11.3 转置和翻转的组合等价性
我们可以证明转置和翻转的组合等价于旋转:
- 转置操作:(i,j) -> (j,i)
- 左右翻转操作:(j,i) -> (j,n-1-i)
- 组合结果:(i,j) -> (j,n-1-i)
这正是顺时针旋转90度的结果。
相关文章:

Java详解LeetCode 热题 100(20):LeetCode 48. 旋转图像(Rotate Image)详解
文章目录 1. 题目描述2. 理解题目3. 解法一:转置 翻转3.1 思路3.2 Java代码实现3.3 代码详解3.4 复杂度分析3.5 适用场景 4. 解法二:四点旋转法4.1 思路4.2 Java代码实现4.3 代码详解4.4 复杂度分析4.5 适用场景 5. 详细步骤分析与示例跟踪5.1 解法一&a…...

CAU人工智能class4 批次归一化
归一化 在对输入数据进行预处理时会用到归一化,将输入数据的范围收缩到0到1之间,这有利于避免纲量对模型训练产生的影响。 但当模型过深时会产生下述问题: 当一个学习系统的输入分布发生变化时,这种现象称之为“内部协变量偏移”…...

Android11以上通过adb复制文件到内置存储让文件管理器可见
之前Android版本如果需要将文件通过adb push放到内置存储,push到/data/media/10下的目录即可,直接放/sdcard/文件管理器是看不到的。 现在最新的Android版本直接将文件放在/sdcard或/data/media/10下文件管理器也看不到 可以将文件再复制一份到一下路径…...

Keepalived 与 LVS 集成及多实例配置详解
一、Keepalived 扩展功能:LVS 集成与多实例管理 1. Keepalived LVS:四层负载均衡高可用方案 1.1 集成原理与架构 核心逻辑:Keepalived 通过 VRRP 实现 LVS 负载均衡节点的高可用,同时利用 LVS 的 IP 负载均衡技术(N…...

篇章二 需求分析(一)
目录 1.知名MQ 2.需求分析 2.1 核心概念 2.2 生产者消费者模型的类别 2.3 BrokerServer 内部的关键概念(MQ) 1.虚拟主机(Virtual Host) 2.交换机(Exchange) 3.队列(Queue) 4…...
)
汽车充电过程中--各个电压的关系(DeepSeek)
在电动汽车的充电过程中,电池的充电机制涉及多个电压参数的协调控制,以下从原理到实际应用逐步分析: 1. 充电基础原理 电动汽车电池(通常为锂离子电池组)的充电本质是通过外部电源向电池注入电能,使锂离子…...
图解深度学习 - 机器学习简史
前言 深度学习并非总是解决问题的最佳方案:缺乏足够数据时,深度学习难以施展;某些情况下,其他机器学习算法可能更为高效。 若初学者首次接触的是深度学习,可能会形成一种偏见,视所有机器学习问题为深度学…...

Gmsh 代码深度解析与应用实例
在科学计算与工程仿真领域,Gmsh 是一款广受欢迎的开源有限元网格生成器,它不仅支持复杂的几何建模,还能高效生成高质量的网格,并具备强大的后处理功能。本文将深入解析几段具有代表性的 Gmsh 代码,从基础几何创建到高级…...

49页 @《人工智能生命体 新启点》中國龍 原创连载
《 人工智能生命体 新启点 》一书,以建立意识来建立起生命体,让其成为独立、自主的活动个体;也就可以理解为建立生命体的思想指导。 让我们能够赋予他灵魂!...

量化研究---bigquant策略交易api研究
api接口来平台的代码整理,原理是读取bigquant的模拟测试信号,下单,可以完美的对接qmt交易,我优化了交易api的部分内容 我开发对接qmt的交易系统 看api源代码 源代码 # 导入系统包 import os import json import requests from ty…...

编译原理 期末速成
一、基本概念 1. 翻译程序 vs 编译程序 翻译程序的三种方式 编译:将高级语言编写的源程序翻译成等价的机器语言或汇编语言。(生成文件,等价)解释:将高级语言编写的源程序翻译一句执行一句,不生成目标文件…...

echarts之漏斗图
vue3echarts实现漏斗图 echarts中文官网:https://echarts.apache.org/examples/zh/index.html 效果图如下: 整体代码如下: <template><div id"funnelChart" style"width:100%;height:400px;"></div&g…...

零基础设计模式——第二部分:创建型模式 - 原型模式
第二部分:创建型模式 - 5. 原型模式 (Prototype Pattern) 我们已经探讨了单例、工厂方法、抽象工厂和生成器模式。现在,我们来看创建型模式的最后一个主要成员——原型模式。这种模式关注的是通过复制现有对象来创建新对象,而不是通过传统的…...

Honeywell TK-PRS021 C200
Honeywell C200/C200E 是一款高性能的集成控制与安全系统(ICSS),采用紧凑型 A 系列机箱 设计,适用于工业自动化、过程控制和批处理管理。C200 控制器最初随 PlantScape R200 发布,而 C200E 则与 Experion PKS R400 兼容…...

java 进阶 1.0.3
Thread API说明 自己滚去看文档 CPU线程调度 每一个线程的优先使用权都是系统随机分配的,人人平等 谁先分配到就谁先用 也可以耍赖,就是赋予某一个线程拥有之高使用权:优先级 这样的操作就叫做线程调度 最基本的是系统轮流获得 java的做法是抢…...

从 Docker 到 runC
从 Docker 到 runC:容器底层原理详解 目录 1. Docker 与 runC 的关系 2. Docker 的核心组件 3. runC 的核心功能 4. 实战示例:从 Docker 到 runC 4.1 示例场景:运行一个简单容器 4.2 Docker 底层调用 runC 的流程 4.3 查看 runC 的调用 4.4 直接调用 runC 创建容器 …...

PET,Prompt Tuning,P Tuning,Lora,Qlora 大模型微调的简介
概览 到2025年,虽然PET(Pattern-Exploiting Training)和Prompt Tuning在学术界仍有探讨,但在工业和生产环境中它们已基本被LoRA/QLoRA等参数高效微调(PEFT)方法取代 。LoRA因其实现简单、推理零开销&#…...

02-jenkins学习之旅-基础配置
0 配置主路径 jenkins安装目录下找到jenkins.xml文件,C:\ProgramData\Jenkins\.jenkins目录下会存放jenkins相关的配置信息。 1 jdk配置 jenkins是java开发开源的项目,进而服务器需要jdk环境 1.1 服务器安装jdk 1.2 jenkins jdk配置 2 git配置 在je…...

互联网大厂Java求职面试:云原生架构与AI应用集成解决方案
互联网大厂Java求职面试:云原生架构与AI应用集成解决方案 场景一:短视频与直播平台的高并发架构设计 面试官提问 面试官(技术总监): 郑薪苦,你有处理过千万级用户同时在线的直播系统吗?如何设…...

Python爬虫实战:研究Crawley 框架相关技术
1. Crawley 框架相关定义 1.1 网络爬虫定义 网络爬虫是一种按照一定的规则,自动地抓取万维网信息的程序或者脚本。它通过 HTTP 协议与 Web 服务器进行交互,获取网页内容并进行解析处理,是数据采集和信息检索的重要工具。 1.2 Crawley 框架定义 Crawley 是一个基于 Pytho…...

C#实现List导出CSV:深入解析完整方案
C#实现List导出CSV:深入解析完整方案 在数据交互场景中,CSV文件凭借其跨平台兼容性和简洁性,成为数据交换的重要载体。本文将基于C#反射机制实现的通用CSV导出方案,结合实际开发中的痛点,从基础实现、深度优化到生产级…...

Appium+python自动化(三)- SDK Manager
简介 一开始打算用真机做的,所以在前边搭建环境时候就没有下载SDK,但是考虑到绝大多数人都没有真机,所以顺应民意整理一下模拟器。SDK顾名思义,Android SDK Manager就是一个Android软件开发工具包管理器,就像一个桥梁&…...

3D Gaussian Splatting for Real-Time Radiance Field Rendering——文章方法精解
SfM → Point-NeRF → 3D Gaussian Splatting 🟦SfM Structure-from-Motion(运动恢复结构,简称 SfM)是一种计算机视觉技术,可以: 利用多张从不同角度拍摄的图像,恢复出场景的三维结构和相机的…...

主成分分析基本概念及python代码使用
目录 1. 前言 2. 主成分分析的基本概念 3. PCA的适应场景 4. PCA算法的理论基础 4.1 标准化数据 4.2 计算协方差矩阵 4.3 求解特征值和特征向量 4.4 选择主成分 4.5 投影到新坐标系 5. 完整的PCA示例 5.1 使用手写数字数据集 5.2 可视化降维后的数据 6. PCA的优缺…...

MCP如何助力智能交通系统?从数据融合到精准决策
MCP如何助力智能交通系统?从数据融合到精准决策 近年来,智能交通系统(ITS)正在全球范围内快速发展,它结合人工智能(AI)、物联网(IoT)和数据分析,致力于提高交通效率、减少拥堵、增强安全性。而MCP(Multi-Constraint Pathfinding,多约束路径寻优)技术作为一种复杂…...

什么是抽象类?是所有函数都是纯虚函数吗?
什么是抽象类? 抽象类(Abstract Class)是一种特殊的类,它不能被直接实例化,但可以作为基类被其他类继承。抽象类的主要用途是定义一组接口规范,这些规范由派生类实现。 在C中,抽象类是通过包含…...

计算机视觉与深度学习 | Python实现ARIMA-WOA-CNN-LSTM时间序列预测(完整源码和数据
以下是一个结合ARIMA、鲸鱼优化算法(WOA)、CNN和LSTM进行时间序列预测的Python实现框架。由于完整代码和数据量较大,此处提供核心代码结构和示例数据集,您可根据需求扩展。 1. 数据准备(示例数据) 使用airline-passengers.csv(航空乘客数据集): import pandas as pd…...

【Unity实战笔记】第二十四 · 使用 SMB+Animator 实现基础战斗系统
转载请注明出处:🔗https://blog.csdn.net/weixin_44013533/article/details/146409453 作者:CSDN|Ringleader| 1 结构 1.1 状态机 1.2 SMB 2 代码实现 2.1 核心控制 Player_Base_SMB 继承 StateMachineBehaviour ,控制变量初始…...

C/C++的OpenCV 进行图像梯度提取
使用 C/OpenCV 进行图像梯度提取 图像梯度表示图像中像素强度的变化率和方向。它是图像分析中的一个基本概念,广泛应用于边缘检测、特征提取和物体识别等任务。OpenCV 提供了多种计算图像梯度的函数。本文将介绍几种常用的梯度算子及其在 C/OpenCV 中的实现。 预备…...

Redis 缓存使用的BigKey问题
一、什么是 BigKey? BigKey 指在 Redis 中存储的 单个 Key 对应的 Value 过大,通常表现为: String 类型:Value 长度 > 10KB。Hash/List/Set/ZSet:元素数量 > 5,000 或总大小 > 10MB。 二、BigKey 的危害 问…...
