【C/C++】红黑树插入/删除修复逻辑解析
文章目录
- 红黑树插入修复逻辑解析
- ✅ 函数原型
- ✅ 外层循环条件
- ✅ 拿到祖父节点
- ✅ Case 1:父节点是祖父的左孩子
- ① 叔叔节点是红色 → 情况1:**颜色翻转(Recolor)**
- ② 叔叔节点是黑色或为空 → 情况2或3:**旋转 + 颜色修复**
- ✅ Case 2:父节点是祖父的右孩子(对称处理)
- ❗ 这个地方有个**严重 bug**:
- 后续逻辑和 Case 1 是对称的:
- ✅ 循环退出后,把根节点设为黑色
- 完整代码示意(带图解)
- ✅ 总结五大逻辑结构
- 红黑树删除修复逻辑解析
- 🔧 函数签名与入口判断
- 🧩 Case 分支:`x` 是左子节点(`x == xParent->left`)
- 📌 Case 1:`w`(兄弟)是红色
- 📌 Case 2:`w` 是黑色,且左右孩子都黑(或空)
- 📌 Case 3:`w` 是黑色,左是红,右是黑
- 📌 Case 4:`w` 是黑色,右是红
- 🔄 对称分支:`x == xParent->right`
- ✅ 最终清理
- 🧠 总结逻辑图(以 `x == xParent->left` 为例)
红黑树插入修复逻辑解析
✅ 函数原型
void InsertFixup(Node* &root, Node *node)
-
root是红黑树的根节点的引用(可变)。 -
node是刚插入的新节点。 -
目标:让树重新满足红黑性质,特别是:
- 不能有两个连续的红色节点(性质 4)
- 根节点必须为黑色(性质 2)
✅ 外层循环条件
while (node != root && node->parent->color == RED)
- 只在当前节点不是根、且父节点是红色时修复。
- 父为红色违反了“红色节点的子节点必须是黑色”的红黑性质。
✅ 拿到祖父节点
Node *gp = node->parent->parent;
- 因为父是红色,说明一定不是根节点 → 父节点有祖父节点。
- 所以这里拿
gp安全。
✅ Case 1:父节点是祖父的左孩子
if (node->parent == gp->left)
然后分成两种情况:
① 叔叔节点是红色 → 情况1:颜色翻转(Recolor)
Node *uncle = gp->right;
if (uncle != nullptr && uncle->color == RED) {node->parent->color = BLACK;uncle->color = BLACK;gp->color = RED;node = gp;
}
- 父和叔都是红的,违反红黑规则。
- 做法是将 父和叔变黑,祖父变红,然后将当前节点指向祖父继续上移修复。
② 叔叔节点是黑色或为空 → 情况2或3:旋转 + 颜色修复
else {if (node == node->parent->right) {node = node->parent;RotateLeft(root, node);}node->parent->color = BLACK;gp->color = RED;RotateRight(root, gp);
}
- 如果当前是“右-左”情况(新节点是父的右子),先左旋变成“左-左”结构。
- 然后右旋祖父,父变为子树新根。
- 同时调整颜色,维持红黑规则。
✅ Case 2:父节点是祖父的右孩子(对称处理)
else {Node *uncle = gp->left;if (uncle->parent->color == RED) {
❗ 这个地方有个严重 bug:
if (uncle->parent->color == RED)
-
这里不应该访问
uncle->parent->color,应该是:if (uncle != nullptr && uncle->color == RED) -
否则当
uncle == nullptr会导致空指针访问崩溃!
后续逻辑和 Case 1 是对称的:
node->parent->color = BLACK;
uncle->color = BLACK;
gp->color = RED;
node = gp;
或者:
if (node == node->parent->left) {node = node->parent;RotateRight(root, node);
}
node->parent->color = BLACK;
gp->color = RED;
RotateLeft(root, gp);
✅ 循环退出后,把根节点设为黑色
root->color = BLACK;
- 保证红黑树“根节点是黑色”这一性质。
完整代码示意(带图解)
void InsertFixup(Node* node) {while (node != root && node->parent != nullptr && node->parent->color == RED) {Node* parent = node->parent;Node* grandparent = parent->parent;if (grandparent == nullptr) break;// Case: parent 是 grandparent 的左孩子if (parent == grandparent->left) {Node* uncle = grandparent->right;if (uncle != nullptr && uncle->color == RED) {/*** Case 1: 叔叔是红色,颜色翻转 + 上移** gp(R) gp(R) 变红后需要向上递归修复* / \ => / \* pa(R) unc(R) pa(B) unc(B)* /* node(R)*/parent->color = BLACK;uncle->color = BLACK;grandparent->color = RED;node = grandparent; // 向上传递修复责任} else {if (node == parent->right) {/*** Case 2: node 是“折弯”结构 —— 需要先转成直线** gp(R)* /* pa(R)* \* node(R)** 先对 parent 左旋*/node = parent;RotateLeft(node);}/*** Case 3: node 是“直线”结构,右旋 grandparent** gp(R) pa(B)* / => / \* pa(R) node(R) gp(R)* /* node(R)*/node->parent->color = BLACK; // parent 变为局部根,染黑grandparent->color = RED;RotateRight(grandparent);node = node->parent; // 当前的 parent 是新的局部根,继续修复}} else {// 对称情况:parent 是右孩子Node* uncle = grandparent->left;if (uncle != nullptr && uncle->color == RED) {/*** Case 1(对称): 叔叔是红色*/parent->color = BLACK;uncle->color = BLACK;grandparent->color = RED;node = grandparent;} else {if (node == parent->left) {/*** Case 2(对称): 折弯结构,先右旋 parent*/node = parent;RotateRight(node);}/*** Case 3(对称): 直线结构,左旋 grandparent*/node->parent->color = BLACK;grandparent->color = RED;RotateLeft(grandparent);node = node->parent;}}}// 最终确保根是黑色,满足性质 2root->color = BLACK;
}✅ 总结五大逻辑结构
| 条件 | 动作 |
|---|---|
| 父红,叔红 | 父、叔设黑,祖父设红,往上递归 |
| 父红,叔黑,新节点在右 | 左旋父 |
| 父红,叔黑,新节点在左 | 父设黑,祖父设红,右旋祖父 |
| 对称情况(父为右子) | 与上面对称处理 |
| 根节点必须为黑色 | 最后强制设 root 为黑 |
红黑树删除修复逻辑解析
🔧 函数签名与入口判断
void DeleteFixup(Node* &root, Node *x, Node *xParent)
x是替代被删除节点的位置,可能是 nullptr。xParent是x的父节点(尤其在x == nullptr时需要)。root是整棵树的引用。
while ((x == nullptr || x->color == BLACK) && x != root)
只要
x是“多余的黑色”,且不是根,就继续修复。
🧩 Case 分支:x 是左子节点(x == xParent->left)
📌 Case 1:w(兄弟)是红色
if (w->color == RED) {w->color = BLACK;xParent->color = RED;RotateLeft(root, xParent);w = xParent->right; // 更新兄弟
}
✅ 通过旋转将兄弟变成黑色,把 Case 1 转换为 Case 2/3/4。
📌 Case 2:w 是黑色,且左右孩子都黑(或空)
if ((w->left == nullptr || w->left->color == BLACK)&& (w->right == nullptr || w->right->color == BLACK)) {w->color = RED;x = xParent;xParent = xParent->parent;
}
✅ 兄弟无法提供黑色,继续向上修复。
📌 Case 3:w 是黑色,左是红,右是黑
if (w->right == nullptr || w->right->color == BLACK) {if (w->left != nullptr) {w->left->color = BLACK;}w->color = RED;RotateRight(root, w);w = xParent->right;
}
✅ 转换成 Case 4。
📌 Case 4:w 是黑色,右是红
w->color = xParent->color;
xParent->color = BLACK;
if (w->right) {w->right->color = BLACK;
}
RotateLeft(root, xParent);
x = root;
✅ 最终修复,黑高恢复,终止循环。
🔄 对称分支:x == xParent->right
代码完全对称,只是把“左”和“右”调换:
- 兄弟变为
xParent->left - 旋转方向反过来:左旋 → 右旋,右旋 → 左旋
- 子节点判断也对称。
✅ 最终清理
if (x != nullptr) {x->color = BLACK;
}
避免残留“多余黑色”。
🧠 总结逻辑图(以 x == xParent->left 为例)
| Case | 条件 | 操作说明 |
|---|---|---|
| 1 | w 是红 | 调色+左旋 → 转为 2/3/4 |
| 2 | w 黑,左右孩子都黑 | 兄弟设红,双黑上移 |
| 3 | w 黑,左红右黑 | 调色 + 右旋兄弟 → 转为 Case 4 |
| 4 | w 黑,右红 | 兄弟右设黑 + 父兄换色 + 左旋 → 修复完成 |
相关文章:

【C/C++】红黑树插入/删除修复逻辑解析
文章目录 红黑树插入修复逻辑解析✅ 函数原型✅ 外层循环条件✅ 拿到祖父节点✅ Case 1:父节点是祖父的左孩子① 叔叔节点是红色 → 情况1:**颜色翻转(Recolor)**② 叔叔节点是黑色或为空 → 情况2或3:**旋转 颜色修复…...

RabbitMQ可靠传输——持久性、发送方确认
一、持久性 前面学习消息确认机制时,是为了保证Broker到消费者直接的可靠传输的,但是如果是Broker出现问题(如停止服务),如何保证消息可靠性?对此,RabbitMQ提供了持久化功能: 持久…...

AWS stop/start 使实例存储lost + 注意点
先看一下官方的说明: EC2有一个特性,当执行stop/start操作(注意,这个并不是重启/reboot,而是先停止/stop,再启动/start)时,该EC2会迁移到其它的底层硬件上。 对于实例存储来说,由于实例存储是由其所在的底层硬件来提供的,此时相当于分配到了一块全新的空的磁盘。 但是从…...

数字计数--数位dp
1.不考虑前导零 2.每一位计数,就是有点“数页码”的意思 P2602 [ZJOI2010] 数字计数 - 洛谷 相关题目:记得加上前导零 数页码--数位dp-CSDN博客 https://blog.csdn.net/2301_80422662/article/details/148160086?spm1011.2124.3001.6209 #include…...

掌握递归:编程中的优雅艺术
当然可以!你愿意迈出学习递归的重要一步,真的很棒!🌟 递归,虽然一开始看着有点绕,但掌握之后,你会发现它是编程中非常优雅且强大的工具。 我用简单又清晰的方式教你。请跟着我一步步来…...

无人机开启未来配送新篇章
低空物流(无人机物流)是利用无人机等低空飞行器进行货物运输的物流方式,依托低空空域(通常在120-300米)实现快速、高效、灵活的配送服务。它是低空经济的重要组成部分,广泛应用于快递配送、医疗物资运输、农…...

el-input宽度自适应方法总结
使用 style 或 class 直接设置宽度 可以通过内联样式或 CSS 类来直接设置 el-input 的宽度为 100%,使其自适应父容器的宽度 <template><div style"width: 100%;"><el-input style"width: 100%;" v-model"input">…...

Qt状态机QStateMachine
QStateMachine QState 提供了一种强大且灵活的方式来表示状态机中的状态,通过与状态机类(QStateMachine)和转换类(QSignalTransition, QEventTransition)结合,可以实现复杂的状态逻辑和用户交互。合理使用嵌套状态机、信号转换、动作与动画、…...

驱动开发学习20250523
kobj_type 功能:表示内核对象类型,描述通过ktype字段嵌入kobject的对象类型,控制在创建和销毁kobject时以及在读取或写入属性时发生的操作。 struct kobj_type {void (*realease)(struct kobject *);const struct sysfs_ops sysfs_ops;stru…...
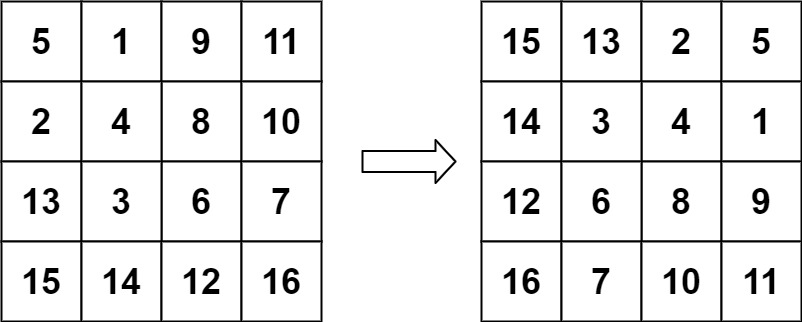
Java详解LeetCode 热题 100(20):LeetCode 48. 旋转图像(Rotate Image)详解
文章目录 1. 题目描述2. 理解题目3. 解法一:转置 翻转3.1 思路3.2 Java代码实现3.3 代码详解3.4 复杂度分析3.5 适用场景 4. 解法二:四点旋转法4.1 思路4.2 Java代码实现4.3 代码详解4.4 复杂度分析4.5 适用场景 5. 详细步骤分析与示例跟踪5.1 解法一&a…...

CAU人工智能class4 批次归一化
归一化 在对输入数据进行预处理时会用到归一化,将输入数据的范围收缩到0到1之间,这有利于避免纲量对模型训练产生的影响。 但当模型过深时会产生下述问题: 当一个学习系统的输入分布发生变化时,这种现象称之为“内部协变量偏移”…...

Android11以上通过adb复制文件到内置存储让文件管理器可见
之前Android版本如果需要将文件通过adb push放到内置存储,push到/data/media/10下的目录即可,直接放/sdcard/文件管理器是看不到的。 现在最新的Android版本直接将文件放在/sdcard或/data/media/10下文件管理器也看不到 可以将文件再复制一份到一下路径…...

Keepalived 与 LVS 集成及多实例配置详解
一、Keepalived 扩展功能:LVS 集成与多实例管理 1. Keepalived LVS:四层负载均衡高可用方案 1.1 集成原理与架构 核心逻辑:Keepalived 通过 VRRP 实现 LVS 负载均衡节点的高可用,同时利用 LVS 的 IP 负载均衡技术(N…...

篇章二 需求分析(一)
目录 1.知名MQ 2.需求分析 2.1 核心概念 2.2 生产者消费者模型的类别 2.3 BrokerServer 内部的关键概念(MQ) 1.虚拟主机(Virtual Host) 2.交换机(Exchange) 3.队列(Queue) 4…...
)
汽车充电过程中--各个电压的关系(DeepSeek)
在电动汽车的充电过程中,电池的充电机制涉及多个电压参数的协调控制,以下从原理到实际应用逐步分析: 1. 充电基础原理 电动汽车电池(通常为锂离子电池组)的充电本质是通过外部电源向电池注入电能,使锂离子…...
图解深度学习 - 机器学习简史
前言 深度学习并非总是解决问题的最佳方案:缺乏足够数据时,深度学习难以施展;某些情况下,其他机器学习算法可能更为高效。 若初学者首次接触的是深度学习,可能会形成一种偏见,视所有机器学习问题为深度学…...

Gmsh 代码深度解析与应用实例
在科学计算与工程仿真领域,Gmsh 是一款广受欢迎的开源有限元网格生成器,它不仅支持复杂的几何建模,还能高效生成高质量的网格,并具备强大的后处理功能。本文将深入解析几段具有代表性的 Gmsh 代码,从基础几何创建到高级…...

49页 @《人工智能生命体 新启点》中國龍 原创连载
《 人工智能生命体 新启点 》一书,以建立意识来建立起生命体,让其成为独立、自主的活动个体;也就可以理解为建立生命体的思想指导。 让我们能够赋予他灵魂!...

量化研究---bigquant策略交易api研究
api接口来平台的代码整理,原理是读取bigquant的模拟测试信号,下单,可以完美的对接qmt交易,我优化了交易api的部分内容 我开发对接qmt的交易系统 看api源代码 源代码 # 导入系统包 import os import json import requests from ty…...

编译原理 期末速成
一、基本概念 1. 翻译程序 vs 编译程序 翻译程序的三种方式 编译:将高级语言编写的源程序翻译成等价的机器语言或汇编语言。(生成文件,等价)解释:将高级语言编写的源程序翻译一句执行一句,不生成目标文件…...

echarts之漏斗图
vue3echarts实现漏斗图 echarts中文官网:https://echarts.apache.org/examples/zh/index.html 效果图如下: 整体代码如下: <template><div id"funnelChart" style"width:100%;height:400px;"></div&g…...

零基础设计模式——第二部分:创建型模式 - 原型模式
第二部分:创建型模式 - 5. 原型模式 (Prototype Pattern) 我们已经探讨了单例、工厂方法、抽象工厂和生成器模式。现在,我们来看创建型模式的最后一个主要成员——原型模式。这种模式关注的是通过复制现有对象来创建新对象,而不是通过传统的…...

Honeywell TK-PRS021 C200
Honeywell C200/C200E 是一款高性能的集成控制与安全系统(ICSS),采用紧凑型 A 系列机箱 设计,适用于工业自动化、过程控制和批处理管理。C200 控制器最初随 PlantScape R200 发布,而 C200E 则与 Experion PKS R400 兼容…...

java 进阶 1.0.3
Thread API说明 自己滚去看文档 CPU线程调度 每一个线程的优先使用权都是系统随机分配的,人人平等 谁先分配到就谁先用 也可以耍赖,就是赋予某一个线程拥有之高使用权:优先级 这样的操作就叫做线程调度 最基本的是系统轮流获得 java的做法是抢…...

从 Docker 到 runC
从 Docker 到 runC:容器底层原理详解 目录 1. Docker 与 runC 的关系 2. Docker 的核心组件 3. runC 的核心功能 4. 实战示例:从 Docker 到 runC 4.1 示例场景:运行一个简单容器 4.2 Docker 底层调用 runC 的流程 4.3 查看 runC 的调用 4.4 直接调用 runC 创建容器 …...

PET,Prompt Tuning,P Tuning,Lora,Qlora 大模型微调的简介
概览 到2025年,虽然PET(Pattern-Exploiting Training)和Prompt Tuning在学术界仍有探讨,但在工业和生产环境中它们已基本被LoRA/QLoRA等参数高效微调(PEFT)方法取代 。LoRA因其实现简单、推理零开销&#…...

02-jenkins学习之旅-基础配置
0 配置主路径 jenkins安装目录下找到jenkins.xml文件,C:\ProgramData\Jenkins\.jenkins目录下会存放jenkins相关的配置信息。 1 jdk配置 jenkins是java开发开源的项目,进而服务器需要jdk环境 1.1 服务器安装jdk 1.2 jenkins jdk配置 2 git配置 在je…...

互联网大厂Java求职面试:云原生架构与AI应用集成解决方案
互联网大厂Java求职面试:云原生架构与AI应用集成解决方案 场景一:短视频与直播平台的高并发架构设计 面试官提问 面试官(技术总监): 郑薪苦,你有处理过千万级用户同时在线的直播系统吗?如何设…...

Python爬虫实战:研究Crawley 框架相关技术
1. Crawley 框架相关定义 1.1 网络爬虫定义 网络爬虫是一种按照一定的规则,自动地抓取万维网信息的程序或者脚本。它通过 HTTP 协议与 Web 服务器进行交互,获取网页内容并进行解析处理,是数据采集和信息检索的重要工具。 1.2 Crawley 框架定义 Crawley 是一个基于 Pytho…...

C#实现List导出CSV:深入解析完整方案
C#实现List导出CSV:深入解析完整方案 在数据交互场景中,CSV文件凭借其跨平台兼容性和简洁性,成为数据交换的重要载体。本文将基于C#反射机制实现的通用CSV导出方案,结合实际开发中的痛点,从基础实现、深度优化到生产级…...
