【NLP 76、Faiss 向量数据库】
压抑与痛苦,那些辗转反侧的夜,终会让我们更加强大
—— 25.5.20
Faiss(Facebook AI Similarity Search)是由 Facebook AI 团队开发的一个开源库,用于高效相似性搜索的库,特别适用于大规模向量数据集的存储与搜索
- 相似性搜索:Faiss 可以高效地搜索大规模向量集合中与查询向量最相似的向量。这对于图像检索、推荐系统、自然语言处理和大数据分析等领域非常有用。
- 多索引结构(软件层面):Faiss 提供了多种索引结构,包括Flat、IVF、HNSW、PQ、LSH 索引等,以满足不同数据集和搜索需求的要求。
- 高性能(硬件层面):Faiss 可利用了多核处理器和 GPU 来加速搜索操作。
- 多语言支持:Faiss 支持 Python、C++ 语言。
- 开源:Faiss 是开源的,可以免费使用和修改,适用于学术研究和商业应用。
一、基本使用
1.基本操作
准备数据
np.random.rand():NumPy 库中用于生成随机数的函数,它返回一个或多个在 [0, 1) 区间内均匀分布的随机数。
| 参数 | 类型 | 描述 | 默认值 |
|---|---|---|---|
| d0, d1, ..., dn | int (可选) | 指定输出数组的形状。如果不提供任何参数,则返回单个随机浮点数。 | 无(必须至少提供一个维度) |
dim:定义向量维度
# 1.1 定义数据和向量维度data = np.random.rand(10000, 256)dim = 256 # 存储的向量维度Ⅰ、创建向量数据库(索引)
① API函数
faiss.IndexFlatL2():创建一个使用 L2 距离(欧氏距离) 进行向量相似度搜索的 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
欧氏(L2)距离公式:

faiss.IndexFlatIP(): 创建一个使用 内积(点积) 进行相似度搜索的 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
点积公式:
 ② 工厂函数
② 工厂函数
faiss.index_factory():通过字符串描述创建 Faiss 索引,支持多种索引类型(如 "IVF100,Flat")。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
description | str | 索引描述字符串(如 "IVF100,Flat") |
metric | int (可选) | 距离度量( |
# 1.2 创建向量数据库(索引)对象 API函数index1 = faiss.IndexFlatL2(dim) # Flat:线性搜索 (O(n)) L2:使用欧式距离计算相似度 dim: 向量维度index2 = faiss.IndexFlatIP(dim) # Flat:线性搜索 (O(n)) IP:使用点积计算相似度 dim: 向量维度# 1.3 创建向量数据库(索引)对象 工厂函数index3 = faiss.index_factory(dim, "Flat", faiss.METRIC_L2) # Flat:线性搜索 (O(n)) L2:使用欧式距离计算相似度 dim: 向量维度index4 = faiss.index_factory(dim, "Flat", faiss.METRIC_INNER_PRODUCT) # Flat:线性搜索 (O(n)) INNER_PRODUCT:使用点积计算相似度 dim: 向量维度Ⅱ、添加向量
向量数据库对象(索引).add():向向量数据库(索引)中添加向量数据。
| 参数 | 类型 | 描述 |
|---|---|---|
xb | np.array | 待添加的向量数组(形状 (n, d)) |
# 2.添加向量index1.add(data)index2.add(data)index3.add(data)index4.add(data)Ⅲ、搜索向量
np.random.rand():NumPy 库中用于生成随机数的函数,它返回一个或多个在 [0, 1) 区间内均匀分布的随机数。
| 参数 | 类型 | 描述 | 默认值 |
|---|---|---|---|
| d0, d1, ..., dn | int (可选) | 指定输出数组的形状。如果不提供任何参数,则返回单个随机浮点数。 | 无(必须至少提供一个维度) |
向量数据库对象(索引).search():在向量数据库(索引)中搜索最相似的 k 个向量。
| 参数 | 类型 | 描述 |
|---|---|---|
xq | np.array | 查询向量(形状 (m, d)) |
k | int | 返回的最近邻数量 |
D:Distance 两向量相似度
I:最相似的向量的索引
# 3.搜索向量query_vectors = np.random.rand(2, 256) # 创建两个 256 维的向量作为查询向量# query_vectors: 待搜索的向量 k: 返回的向量个数D, I = index1.search(query_vectors, k=2)# D: Distance 两向量相似度 I: Index 返回最相似的向量的索引print("index1_D:", D, "index1_I:", I)D, I = index2.search(query_vectors, k=2)print("index2_D:", D, "index2_I:", I)D, I = index3.search(query_vectors, k=2)print("index3_D:", D, "index3_I:", I)D, I = index4.search(query_vectors, k=2)print("index4_D:", D, "index4_I:", I)Ⅳ、删除向量
np.array():将 Python 列表或类似结构转换为 NumPy 数组。
| 参数 | 类型 | 描述 |
|---|---|---|
data | list/array-like | 输入数据 |
dtype | str/np.dtype (可选) | 数据类型(如 'float32') |
向量数据库对象(索引).remove_ids():从索引中删除指定 ID 的向量。
| 参数 | 类型 | 描述 |
|---|---|---|
ids | np.array/list | 要删除的向量 ID 列表 |
向量数据库对象(索引).reset():清空索引中的所有向量。
向量数据库对象(索引).ntotal:返回索引中当前存储的向量数量(属性,非函数)。
# 4.删除向量index1.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index1剩余向量个数为:", index1.ntotal) # 打印剩余的向量个数index2.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index2剩余向量个数为:", index2.ntotal) # 打印剩余的向量个数index3.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index3剩余向量个数为:", index3.ntotal) # 打印剩余的向量个数index4.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index4剩余向量个数为:", index4.ntotal) # 打印剩余的向量个数index3.reset() # 删除全部向量print("index3剩余向量个数为:", index3.ntotal) # 打印剩余的向量个数Ⅴ、存储向量数据库(索引)
faiss.write_index():将 Faiss 索引保存到磁盘。
| 参数 | 类型 | 描述 |
|---|---|---|
index | faiss.Index | Faiss 索引对象 |
file_path | str | 保存路径 |
faiss.write_index(index1, 'flat.faiss')Ⅵ、加载向量数据库(索引)
faiss.read_index():从磁盘加载 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
file_path | str | 索引文件路径 |
faiss.read_index('flat.faiss')Ⅶ、完整代码
import faiss
import numpy as npnp.random.seed(0)# 一、基本操作
def test01():# 1.构建索引(向量数据库)# 1.1 定义数据和向量维度data = np.random.rand(10000, 256)dim = 256 # 存储的向量维度# 1.2 创建索引对象 API函数index1 = faiss.IndexFlatL2(dim) # Flat:线性搜索 (O(n)) L2:使用欧式距离计算相似度 dim: 向量维度index2 = faiss.IndexFlatIP(dim) # Flat:线性搜索 (O(n)) IP:使用点积计算相似度 dim: 向量维度# 1.3 创建索引对象 工厂函数index3 = faiss.index_factory(dim, "Flat", faiss.METRIC_L2) # Flat:线性搜索 (O(n)) L2:使用欧式距离计算相似度 dim: 向量维度index4 = faiss.index_factory(dim, "Flat", faiss.METRIC_INNER_PRODUCT) # Flat:线性搜索 (O(n)) INNER_PRODUCT:使用点积计算相似度 dim: 向量维度# 2.添加向量index1.add(data)index2.add(data)index3.add(data)index4.add(data)# 3.搜索向量query_vectors = np.random.rand(2, 256) # 创建两个 256 维的向量作为查询向量# query_vectors: 待搜索的向量 k: 返回的向量个数D, I = index1.search(query_vectors, k=2)# D: Distance 两向量相似度 I: Index 返回最相似的向量的索引print("index1_D:", D, "index1_I:", I)D, I = index2.search(query_vectors, k=2)print("index2_D:", D, "index2_I:", I)D, I = index3.search(query_vectors, k=2)print("index3_D:", D, "index3_I:", I)D, I = index4.search(query_vectors, k=2)print("index4_D:", D, "index4_I:", I)# 4.删除向量index1.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index1剩余向量个数为:", index1.ntotal) # 打印剩余的向量个数index2.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index2剩余向量个数为:", index2.ntotal) # 打印剩余的向量个数index3.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index3剩余向量个数为:", index3.ntotal) # 打印剩余的向量个数index4.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index4剩余向量个数为:", index4.ntotal) # 打印剩余的向量个数index3.reset() # 删除全部向量print("index3剩余向量个数为:", index3.ntotal) # 打印剩余的向量个数# 5.存储索引faiss.write_index(index1, 'flat.faiss')# 6.加载索引faiss.read_index('flat.faiss')if __name__ == '__main__':test01()
2.ID映射
Ⅰ、创建向量数据库(索引)
faiss.IndexFlatL2():创建一个使用 L2 距离(欧氏距离) 进行向量相似度搜索的 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
欧氏(L2)距离公式:

# 1.创建索引(向量数据库)index = faiss.IndexFlatL2(256)Ⅱ、⭐ 包装向量数据库(索引)
实现自定义向量编号
faiss.IndexIDMap():为索引添加自定义 ID 映射,支持按 ID 管理向量。
| 参数 | 类型 | 描述 |
|---|---|---|
index | faiss.Index | 底层索引(如 IndexFlatL2) |
# 2.包装索引:实现自定义向量编号index = faiss.IndexIDMap(index)Ⅲ、添加向量【准备数据】
np.random.rand():生成 [0, 1) 区间均匀分布的随机数组。
| 参数 | 类型 | 描述 |
|---|---|---|
d0, d1, ..., dn | int (可选) | 数组形状 |
向量数据库对象(索引).add_with_ids():添加向量并指定自定义 ID(需配合 IndexIDMap 使用)。
| 参数 | 类型 | 描述 |
|---|---|---|
xb | np.array | 向量数组 |
ids | np.array | 对应的 ID 数组 |
np.arange():生成等间隔数值序列(类似 Python range)。
| 参数 | 类型 | 描述 |
|---|---|---|
start | int/float | 起始值(默认 0) |
stop | int/float | 结束值(不包含) |
step | int/float | 步长(默认 1) |
# 3.添加向量data = np.random.rand(10000, 256)index.add_with_ids(data, np.arange(10000, 20000)) # 向量编号从 10000 开始, 20000 结束Ⅳ、搜索向量
向量数据库对象(索引).ntotal:返回索引中当前存储的向量数量(属性,非函数)。
向量数据库对象(索引).remove_ids():从索引中删除指定 ID 的向量。
| 参数 | 类型 | 描述 |
|---|---|---|
ids | np.array/list | 要删除的向量 ID 列表 |
np.array():将 Python 列表或类似结构转换为 NumPy 数组。
| 参数 | 类型 | 描述 |
|---|---|---|
data | list/array-like | 输入数据 |
dtype | str/np.dtype (可选) | 数据类型(如 'float32') |
# 4.删除索引向量print("index1向量个数为:", index.ntotal) # 打印向量个数index.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index1剩余向量个数为:", index.ntotal) # 打印剩余的向量个数# 有些索引类型本身支持用户指定 ID,如果不支持的话,可以使用IndexIDMap包装一下Ⅴ、完整代码
import faiss
import numpy as npnp.random.seed(0)# 二、向量 ID 映射
def test02():# 1.创建索引(向量数据库)index = faiss.IndexFlatL2(256)# 2.包装索引:实现自定义向量编号index = faiss.IndexIDMap(index)# 3.添加向量data = np.random.rand(10000, 256)index.add_with_ids(data, np.arange(10000, 20000)) # 向量编号从 10000 开始, 20000 结束# 4.删除索引向量print("index1向量个数为:", index.ntotal) # 打印向量个数index.remove_ids(np.array([0, 1, 2, 3])) # 删除索引为 0, 1, 2, 3 的向量print("index1剩余向量个数为:", index.ntotal) # 打印剩余的向量个数# 有些索引类型本身支持用户指定 ID,如果不支持的话,可以使用IndexIDMap包装一下if __name__ == '__main__':test02()
二、更快的索引
IndexFlat 索引是一种基于线性搜索的索引,它通过逐个计算与每个向量的相似度来进行搜索。在数据量较大的时候,搜索效率会较低。此时,我们可以使用 IndexIVFFlat 索引来提升搜索效率。它的原理如下:对于所有的向量进行聚类,相当于把所有的数据进行分类。当进行查询时,在最相似的 N 个簇中进行线性搜索。这就减少了需要进行相似度计算的数据量,从而提升搜索效率。
需要注意:这种方法是一种在查询的精度和效率之间平衡的方法。簇数目越多,精度越高,效率越低

1.定义数据和向量维度
np.random.rand():生成等间隔数值序列(类似 Python range)
| 参数 | 类型 | 描述 |
|---|---|---|
start | int/float | 起始值(默认 0) |
stop | int/float | 结束值(不包含) |
step | int/float | 步长(默认 1) |
np.arange():生成等间隔数值序列(类似 Python range)。
| 参数 | 类型 | 描述 |
|---|---|---|
start | int/float | 起始值(默认 0) |
stop | int/float | 结束值(不包含) |
step | int/float | 步长(默认 1) |
np.random.seed():设置随机数生成器的种子,确保结果可复现。
| 参数 | 类型 | 描述 |
|---|---|---|
seed | int | 随机种子 |
# 1.1 定义数据和向量维度
data = np.random.rand(1000000, 256)
dim = 256 # 存储的向量维度
ids = np.arange(0, 1000000)
np.random.seed(4)
query_vector = np.random.rand(1, 256)2.线性搜索
faiss.IndexFlatL2():创建一个使用 L2 距离(欧氏距离) 进行向量相似度搜索的 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
欧氏(L2)距离公式:

向量数据库对象(索引).add():向向量数据库(索引)中添加向量数据。
| 参数 | 类型 | 描述 |
|---|---|---|
xb | np.array | 待添加的向量数组(形状 (n, d)) |
time.time():返回当前时间的时间戳(自纪元以来的秒数,浮点数形式)。常用于计算代码执行时间或记录时间点。
向量数据库对象(索引).search():在向量数据库(索引)中搜索最相似的 k 个向量。
| 参数 | 类型 | 描述 |
|---|---|---|
xq | np.array | 查询向量(形状 (m, d)) |
k | int | 返回的最近邻数量 |
D:Distance 两向量相似度
I:最相似的向量的索引
# 使用线性搜索
def test01():# 1.构建索引(向量数据库)# 1.2 创建索引对象 API函数index1 = faiss.IndexFlatL2(dim) # Flat:线性搜索 (O(n)) L2:使用欧式距离计算相似度 dim: 向量维度# 2.添加向量index1.add(data)# 3.搜索向量start = time.time()# query_vector: 待搜索的向量 k: 返回的向量个数D, I = index1.search(query_vector, k=1)# D: Distance 两向量相似度 I: Index 返回最相似的向量的索引print("index1_D:", D, "index1_I:", I)print("method1_time:", time.time() - start)3.聚类搜索
faiss.IndexFlatL2():创建一个使用 L2 距离(欧氏距离) 进行向量相似度搜索的 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
欧氏(L2)距离公式:

faiss.IndexIVFFlat():创建一个基于倒排文件(Inverted File, IVF)和扁平化量化(Flat Quantization)的索引结构。适用于大规模向量搜索,通过聚类减少搜索空间,提升查询效率。
| 参数 | 类型 | 说明 |
|---|---|---|
d | int | 向量维度(必填) |
nlist | int | 聚类中心数量(必填) |
metric | faiss.MetricType | 距离度量方式(默认 faiss.METRIC_L2,即欧氏距离) |
use_precomputed_table | int | 是否使用预计算的码本表(默认 0,不使用) |
向量数据库对象.train():对索引进行训练,需提供一组代表性向量(通常为数据集的子集),用于学习聚类中心或其他模型参数(如量化码本)。训练是构建索引的必要步骤。
| 参数 | 类型 | 说明 |
|---|---|---|
xb | numpy.ndarray | 训练数据矩阵,形状为 (n_samples, d),其中 d 是向量维度 |
niter | int | 训练迭代次数(部分索引类型支持,可选) |
verbose | bool | 是否打印训练日志(可选,默认 False) |
向量数据库对象(索引).add():向向量数据库(索引)中添加向量数据。
| 参数 | 类型 | 描述 |
|---|---|---|
xb | np.array | 待添加的向量数组(形状 (n, d)) |
time.time():返回当前时间的时间戳(自纪元以来的秒数,浮点数形式)。常用于计算代码执行时间或记录时间点。
向量数据库对象(索引).search():在向量数据库(索引)中搜索最相似的 k 个向量。
| 参数 | 类型 | 描述 |
|---|---|---|
xq | np.array | 查询向量(形状 (m, d)) |
k | int | 返回的最近邻数量 |
D:Distance 两向量相似度
I:最相似的向量的索引
# 使用聚类索引 IVF
def test02():# 第一个参数 —— 量化参数:quantizer# 第二个参数 —— 向量维度:dim# 第三个参数 —— 聚类中心个数:nlistquantizer = faiss.IndexFlatL2(dim) # 使用欧式距离计算相似度 dim: 向量维度index = faiss.IndexIVFFlat(quantizer, dim, 100)index.train(data) # 训练索引,找到所有簇的质心# 将向量分配到距离最近的簇中index.add(data) # 添加向量到索引中start = time.time()# 近似相似的搜索D, I = index.search(query_vector, k=1)print("index1_D:", D, "index1_I:", I)print("method2_time:", time.time() - start)4.聚类搜索(指定聚类簇数)
faiss.IndexFlatL2():创建一个使用 L2 距离(欧氏距离) 进行向量相似度搜索的 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
欧氏(L2)距离公式:

faiss.IndexIVFFlat():创建一个基于倒排文件(Inverted File, IVF)和扁平化量化(Flat Quantization)的索引结构。适用于大规模向量搜索,通过聚类减少搜索空间,提升查询效率。
| 参数 | 类型 | 说明 |
|---|---|---|
d | int | 向量维度(必填) |
nlist | int | 聚类中心数量(必填) |
metric | faiss.MetricType | 距离度量方式(默认 faiss.METRIC_L2,即欧氏距离) |
use_precomputed_table | int | 是否使用预计算的码本表(默认 0,不使用) |
向量数据库对象.nprobe():设置或获取搜索时的探查聚类中心数量(nprobe)。控制搜索时访问的聚类中心数目,影响查询速度和精度(值越大越精确,但速度越慢)。
| 参数 | 类型 | 说明 |
|---|---|---|
nprobe | int | 要探查的聚类中心数量(仅用于设置时传入) |
向量数据库对象.train():对索引进行训练,需提供一组代表性向量(通常为数据集的子集),用于学习聚类中心或其他模型参数(如量化码本)。训练是构建索引的必要步骤。
| 参数 | 类型 | 说明 |
|---|---|---|
xb | numpy.ndarray | 训练数据矩阵,形状为 (n_samples, d),其中 d 是向量维度 |
niter | int | 训练迭代次数(部分索引类型支持,可选) |
verbose | bool | 是否打印训练日志(可选,默认 False) |
向量数据库对象(索引).add():向向量数据库(索引)中添加向量数据。
| 参数 | 类型 | 描述 |
|---|---|---|
xb | np.array | 待添加的向量数组(形状 (n, d)) |
向量数据库对象(索引).search():在向量数据库(索引)中搜索最相似的 k 个向量。
| 参数 | 类型 | 描述 |
|---|---|---|
xq | np.array | 查询向量(形状 (m, d)) |
k | int | 返回的最近邻数量 |
time.time():返回当前时间的时间戳(自纪元以来的秒数,浮点数形式)。常用于计算代码执行时间或记录时间点。
D:Distance 两向量相似度
I:最相似的向量的索引
# 使用聚类索引 IVF 效率与准确率平衡
def test03():# 第一个参数 —— 量化参数:quantizer# 第二个参数 —— 向量维度:dim# 第三个参数 —— 聚类中心个数:nlistquantizer = faiss.IndexFlatL2(dim) # 使用欧式距离计算相似度 dim: 向量维度index = faiss.IndexIVFFlat(quantizer, dim, 100)index.nprobe = 10 # 指定在最相似的前多少个簇中进行线性搜索index.train(data) # 训练索引,找到所有簇的质心# 将向量分配到距离最近的簇中index.add(data) # 添加向量到索引中start = time.time()# 近似相似的搜索D, I = index.search(query_vector, k=1)print("index1_D:", D, "index1_I:", I)print("method2_plus_time:", time.time() - start)5.完整代码
import faiss
import numpy as np
import time# 1.1 定义数据和向量维度
data = np.random.rand(1000000, 256)
dim = 256 # 存储的向量维度
ids = np.arange(0, 1000000)
np.random.seed(4)
query_vector = np.random.rand(1, 256)# 使用线性搜索
def test01():# 1.构建索引(向量数据库)# 1.2 创建索引对象 API函数index1 = faiss.IndexFlatL2(dim) # Flat:线性搜索 (O(n)) L2:使用欧式距离计算相似度 dim: 向量维度# 2.添加向量index1.add(data)# 3.搜索向量start = time.time()# query_vector: 待搜索的向量 k: 返回的向量个数D, I = index1.search(query_vector, k=1)# D: Distance 两向量相似度 I: Index 返回最相似的向量的索引print("index1_D:", D, "index1_I:", I)print("method1_time:", time.time() - start)# 使用聚类索引 IVF
def test02():# 第一个参数 —— 量化参数:quantizer# 第二个参数 —— 向量维度:dim# 第三个参数 —— 聚类中心个数:nlistquantizer = faiss.IndexFlatL2(dim) # 使用欧式距离计算相似度 dim: 向量维度index = faiss.IndexIVFFlat(quantizer, dim, 100)index.train(data) # 训练索引,找到所有簇的质心# 将向量分配到距离最近的簇中index.add(data) # 添加向量到索引中start = time.time()# 近似相似的搜索D, I = index.search(query_vector, k=1)print("index1_D:", D, "index1_I:", I)print("method2_time:", time.time() - start)# 使用聚类索引 IVF 效率与准确率平衡
def test03():# 第一个参数 —— 量化参数:quantizer# 第二个参数 —— 向量维度:dim# 第三个参数 —— 聚类中心个数:nlistquantizer = faiss.IndexFlatL2(dim) # 使用欧式距离计算相似度 dim: 向量维度index = faiss.IndexIVFFlat(quantizer, dim, 100)index.nprobe = 10 # 指定在最相似的前多少个簇中进行线性搜索index.train(data) # 训练索引,找到所有簇的质心# 将向量分配到距离最近的簇中index.add(data) # 添加向量到索引中start = time.time()# 近似相似的搜索D, I = index.search(query_vector, k=1)print("index1_D:", D, "index1_I:", I)print("method2_plus_time:", time.time() - start)if __name__ == '__main__':test01()print("————————————————————————————————")test02()print("————————————————————————————————")test03()# 这种方法是一种在查询的精度和效率之间平衡的方法。 # time 与 nprobe 的关系是:nprobe 越大,查询的精度越高,但是查询的时间也会增加。
三、更少的内存
前面的几个索引类型为了实现向量搜索,都需要将向量存储到 Faiss 中,当向量的数量较多时就会占用更多的内存。 这也影响了 Faiss 的应用。所以,为了减少内存的占用,我们就需要会存储的向量进行重新编码、压缩,使其占用更少的内存,从而能够容纳更多的向量。
量化技术可以使用较低精度的表示来近似向量数据,从而降低内存需求而又不牺牲准确性。 这对于大规模向量相似性搜索应用程序特别有用。
1.PQ量化压缩
Product Quantization 是一种有效的近似最近邻搜索方法,具有较高的搜索效率和较低的内存消耗。该方法已被广泛应用于图像检索、文本检索和机器学习等领域。
PQ 将高维数据点分成多个子空间,并对每个子空间使用独立的编码方法,将数据点映射到一个有限的编码集合中。这个编码过程将高维数据转换成低维编码,从而降低了存储和计算的成本。
例如,我们有 N 个 1024 维的数据点:

将每个向量划分为 8 个 128 维的子向量 subvectors,更多的子向量划分意味着将原始向量空间划分为更多的子空间进行量化,有助于减少量化误差。

对每一组子向量进行聚类,这里簇的数量为 256,聚类的质心数量越多,误差就越小。如下:

聚类之后的每个 subvector 的质心可以作为码本,用于将子向量映射到一个整数。
此时,当我们拿到某一个 1×1024 的数据时,我们就可以通过下面的过程将其量化(用每一个子向量所属质心的编号来表示):

最终得到结果,量化前:1 × 1024 = 1024 字节,量化后:1 × 8 = 8 字节
代码实现
np.random.rand():是 NumPy 库中的一个函数,用于生成指定形状的数组,数组中的元素是从均匀分布中随机采样的,范围在 [0, 1) 之间。
| 参数 | 类型 | 说明 |
|---|---|---|
d0, d1, ..., dn | int, 可选 | 定义输出数组的维度。如果不提供任何参数,则返回一个浮点数(标量)。 |
faiss.ProductQuantizer():是 Faiss 库中的一个类,用于实现乘积量化(Product Quantization, PQ)。乘积量化是一种高效的向量压缩和搜索技术,通过将高维向量分解为多个低维子向量,并对每个子向量进行独立量化,从而减少存储空间并加速搜索过程。
| 参数 | 类型 | 说明 |
|---|---|---|
d | int | 向量的总维度(必填)。 |
M | int | 子向量的数量,即将原始向量分成 M 个子向量,每个子向量的维度为 d // M(必填)。 |
nbits | int, 可选 | 每个子量化的码本大小(即每个子向量使用的比特数),默认是 8,对应 256 个码字。 |
metric_type | faiss.MetricType, 可选 | 距离度量类型,默认是 faiss.METRIC_L2(欧氏距离)。可选值包括 faiss.METRIC_INNER_PRODUCT 等。 |
train_type | faiss.ProductQuantizer.TrainType, 可选 | 训练类型,控制训练过程的行为,默认是 faiss.ProductQuantizer.TrainType.DEFAULT。 |
pq:创建一个 Product Quantizer (PQ) 对象,用于将 32 维向量 压缩为 8 个子向量,每个子向量用 8 比特(256 个码字) 进行量化。
pq.train():训练乘积量化(PQ)的码本(codebook),学习每个子向量的量化中心。
需要提供足够多样本的训练数据,使码本能覆盖数据的分布特征。
训练完成后,才能进行向量编码(compute_codes())。
| 参数 | 类型 | 说明 |
|---|---|---|
x | numpy.ndarray | 训练数据矩阵,形状为 (n_samples, d),dtype=float32(必填)。其中 d 必须与 ProductQuantizer 初始化时的维度一致。 |
pq.compute_codes():将输入向量编码为压缩后的码字(整数数组)。
每个子向量会被映射到其对应的量化中心(由码本定义),最终输出一个紧凑的码字表示。编码后的码字可用于存储或快速检索。
| 参数 | 类型 | 说明 |
|---|---|---|
x | numpy.ndarray | 待编码的向量矩阵,形状为 (n_samples, d),dtype=float32(必填)。其中 d 必须与 ProductQuantizer 初始化时的维度一致。 |
pq.decode():将码字解码为近似原始向量(通过码本中的量化中心重建)。
由于量化存在误差,解码后的向量可能与原始向量不完全相同,但能显著减少存储和计算开销。
| 参数 | 类型 | 说明 |
|---|---|---|
codes | numpy.ndarray | 输入的码字矩阵,形状为 (n_samples, M),dtype=uint8 或 int32(必填)。每个元素必须是 0 到 2^nbits - 1 的整数。 |
import faiss
import numpy as npdef test():data = np.random.rand(10000, 32).astype('float32')# 训练码本(向量维度、子向量数量、子向量质心数量(位数))pq = faiss.ProductQuantizer(32, 8, 8)# pq.verbose = Truepq.train(data)# 编码量化x1 = np.random.rand(1, 32).astype('float32')x2 = pq.compute_codes(x1)# 解码量化x3 = pq.decode(x2)print('原始向量:\n', x1)print('编码量化:\n', x2)print('解码量化:\n', x3)if __name__ == '__main__':test()
2.定义数据和向量维度
np.random.seed():设置随机数生成器的种子,确保每次运行代码时生成的随机数序列相同(可复现性)。常用于调试或实验中需要固定随机结果的情况。
| 参数 | 类型 | 说明 |
|---|---|---|
seed | int 或 None | 随机数种子(整数)。若为 None,则使用系统时间作为种子(默认行为)。 |
np.random.rand():生成指定形状的数组,元素从均匀分布 [0, 1) 中随机采样。
| 参数 | 类型 | 说明 |
|---|---|---|
d0, d1, ..., dn | int, 可选 | 定义输出数组的维度。若无参数,返回单个浮点数。 |
np.arrange():生成一个等差数列数组,类似于 Python 内置的 range(),但返回的是 NumPy 数组而非列表。
| 参数 | 类型 | 说明 |
|---|---|---|
start | number, 可选 | 起始值(默认 0)。 |
stop | number | 结束值(不包含该值)。 |
step | number, 可选 | 步长(默认 1)。 |
dtype | dtype, 可选 | 输出数组的数据类型(默认推断)。 |
np.random.rand():NumPy 库中的一个函数,用于生成指定形状的数组,数组中的元素是从均匀分布中随机采样的,范围在 [0, 1) 之间。
| 参数 | 类型 | 说明 |
|---|---|---|
d0, d1, ..., dn | int, 可选 | 定义输出数组的维度。如果不提供任何参数,则返回一个浮点数(标量)。 |
np.random.seed(0)
data = np.random.rand(1000000, 256)
ids = np.arange(0, 1000000)
query_vector = np.random.rand(1, 256)3.线性搜索
faiss.IndexFlatL2():创建一个使用 L2 距离(欧氏距离) 进行向量相似度搜索的 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
欧氏(L2)距离公式:

faiss.IndexIDMap():将外部ID映射到Faiss索引的内部向量ID,允许通过用户自定义的ID(如数据库ID)检索向量,而非Faiss自动生成的连续整数ID。
| 参数 | 类型 | 说明 |
|---|---|---|
index | faiss.Index | 基础Faiss索引对象(必填)。 |
own_fields | bool | 是否接管基础索引的所有权(默认 False)。 |
向量数据库对象(索引).add_with_ids(): 向Faiss索引中添加向量及其对应的自定义ID(需配合IndexIDMap使用),实现通过外部ID检索向量。
| 参数 | 类型 | 说明 |
|---|---|---|
x | numpy.ndarray | 向量数据,形状为 (n, d),dtype=float32(必填)。 |
ids | numpy.ndarray | 对应的自定义ID数组,形状为 (n,),dtype=long(必填)。 |
time.time():返回当前时间的时间戳(自纪元以来的秒数,浮点数形式)。常用于计算代码执行时间或记录时间点。
向量数据库对象(索引).search():在向量数据库(索引)中搜索最相似的 k 个向量。
| 参数 | 类型 | 描述 |
|---|---|---|
xq | np.array | 查询向量(形状 (m, d)) |
k | int | 返回的最近邻数量 |
D:Distance 两向量相似度
I:最相似的向量的索引
faiss.write_index():将Faiss索引保存到磁盘文件,支持后续加载复用。
| 参数 | 类型 | 说明 |
|---|---|---|
index | faiss.Index | 要保存的Faiss索引对象(必填)。 |
filename | str | 目标文件路径(必填)。 |
os.stat():获取文件或目录的状态信息(如大小、修改时间等),返回一个os.stat_result对象。
| 参数 | 类型 | 说明 |
|---|---|---|
path | str 或 bytes | 文件/目录路径(必填)。 |
.st_size:从os.stat_result对象中获取文件的大小(字节)。
def test01():index = faiss.IndexFlatL2(256)index = faiss.IndexIDMap(index)# 添加向量index.add_with_ids(data, ids)# 搜索向量s = time.time()D, I = index.search(query_vector, k=2)print('time1:', time.time() - s)print(D, I)faiss.write_index(index, 'flat.faiss')print("space1:", os.stat('flat.faiss').st_size)4.聚类搜索(指定聚类数目)
faiss.IndexFlatL2():创建一个使用 L2 距离(欧氏距离) 进行向量相似度搜索的 Faiss 索引。
| 参数 | 类型 | 描述 |
|---|---|---|
d | int | 向量的维度 |
欧氏(L2)距离公式:

faiss.IndexIVFFlat():创建基于倒排文件(IVF)和扁平化量化(Flat)的索引结构,用于高效的大规模向量搜索。通过聚类减少搜索空间,显著提升查询速度。
| 参数 | 类型 | 说明 |
|---|---|---|
d | int | 向量维度(必填)。 |
nlist | int | 聚类中心数量(必填)。 |
metric | faiss.MetricType | 距离度量方式(默认 faiss.METRIC_L2,即欧氏距离)。 |
use_precomputed_table | int | 是否使用预计算的码本表(默认 0,不使用)。 |
向量数据库对象.nprobe():设置或获取搜索时的探查聚类中心数量(nprobe)。控制搜索时访问的聚类中心数目,影响查询速度和精度(值越大越精确,但速度越慢)。
| 参数 | 类型 | 说明 |
|---|---|---|
nprobe | int | 要探查的聚类中心数量(仅用于设置时传入)。 |
向量数据库对象.train():对索引进行训练,需提供一组代表性向量(通常为数据集的子集),用于学习聚类中心或其他模型参数(如量化码本)。训练是构建索引的必要步骤。
| 参数 | 类型 | 说明 |
|---|---|---|
xb | numpy.ndarray | 训练数据矩阵,形状为 (n_samples, d),其中 d 是向量维度 |
niter | int | 训练迭代次数(部分索引类型支持,可选) |
verbose | bool | 是否打印训练日志(可选,默认 False) |
向量数据库对象.add_with_ids():
向量数据库对象(索引).search():在向量数据库(索引)中搜索最相似的 k 个向量。
| 参数 | 类型 | 描述 |
|---|---|---|
xq | np.array | 查询向量(形状 (m, d)) |
k | int | 返回的最近邻数量 |
D:Distance 两向量相似度
I:最相似的向量的索引
time.time():返回当前时间的时间戳(自纪元以来的秒数,浮点数形式)。常用于计算代码执行时间或记录时间点。
faiss.write_index():将Faiss索引保存到磁盘文件,支持后续加载复用。
| 参数 | 类型 | 说明 |
|---|---|---|
index | faiss.Index | 要保存的Faiss索引对象(必填)。 |
filename | str | 目标文件路径(必填)。 |
os.stat():获取文件或目录的状态信息(如大小、修改时间等),返回一个os.stat_result对象。
| 参数 | 类型 | 说明 |
|---|---|---|
path | str 或 bytes | 文件/目录路径(必填)。 |
.st_size:从os.stat_result对象中获取文件的大小(字节)。
def test02():# 第一个参数 —— 量化参数:quantizer# 第二个参数 —— 向量维度:dim# 第三个参数 —— 聚类中心个数:nlistindex = faiss.IndexFlatL2(256)index = faiss.IndexIVFFlat(index, 256, 100)index.nprobe = 4 # 指定在最相似的前多少个簇中进行线性搜索index.train(data) # 训练索引,找到所有簇的质心index.add_with_ids(data, ids)s = time.time()D, I = index.search(query_vector, k=2)print('time2:', time.time() - s)print(D, I)faiss.write_index(index, 'ivfflat.faiss')print("space2:", os.stat('ivfflat.faiss').st_size)5.完整代码
import osimport faiss
import numpy as np
import timenp.random.seed(0)
data = np.random.rand(1000000, 256)
ids = np.arange(0, 1000000)
query_vector = np.random.rand(1, 256)def test01():index = faiss.IndexFlatL2(256)index = faiss.IndexIDMap(index)# 添加向量index.add_with_ids(data, ids)# 搜索向量s = time.time()D, I = index.search(query_vector, k=2)print('time1:', time.time() - s)print(D, I)faiss.write_index(index, 'flat.faiss')print("space1:", os.stat('flat.faiss').st_size)def test02():# 第一个参数 —— 量化参数:quantizer# 第二个参数 —— 向量维度:dim# 第三个参数 —— 聚类中心个数:nlistindex = faiss.IndexFlatL2(256)index = faiss.IndexIVFFlat(index, 256, 100)index.nprobe = 4 # 指定在最相似的前多少个簇中进行线性搜索index.train(data) # 训练索引,找到所有簇的质心index.add_with_ids(data, ids)s = time.time()D, I = index.search(query_vector, k=2)print('time2:', time.time() - s)print(D, I)faiss.write_index(index, 'ivfflat.faiss')print("space2:", os.stat('ivfflat.faiss').st_size)def test03():# 第一个参 —— 量化参数:quantizer# 第二个参数 —— 向量维度:dim# 第三个参数 —— 质心数量:nlist# 第四个参数 —— 聚类中心个数:ncentroids# 第四个参数 —— 子空间数量(或称为段数):p 较大的值意味着将原始向量空间划分为更多的子空间进行量化,有助于减少量化误差,因为每个子空间都将被更精细地量化。# 第五个参数 —— 量化码本中码字的位数,每个段聚类的数量(8位256): q 决定了每个量化码字的精度,位数越多,每个码字能够表示的信息就越多,量化误差就越小。quantizer = faiss.IndexFlatL2(256)index = faiss.IndexIVFPQ(quantizer, 256, 100, 64, 10)index.nprobe = 4index.train(data)index.add_with_ids(data, ids)# 搜索向量s = time.time()D, I = index.search(query_vector, k=2)print('time3:', time.time() - s)print(D, I)faiss.write_index(index, 'ivfpq.faiss')print("space3:", os.stat('ivfpq.faiss').st_size)if __name__ == '__main__':test01()print("————————————————————————————————")test02()print("————————————————————————————————")test03()
四、GPU训练
传统 CPU 计算在处理大规模向量数据时往往效率低下,而 GPU 具有并行计算能力强、吞吐量高、延迟低等优势,可以显著提高向量相似度搜索的速度。例如:在 Faiss 官方提供的基准测试中,使用 GPU 计算的 Faiss 可以将向量相似度搜索的速度提高数十倍甚至数百倍。
faiss.StandardGpuResources():创建 GPU 资源管理对象,用于在 GPU 上执行 Faiss 操作(如索引构建和搜索)。需配合 index_cpu_to_gpu() 将 CPU 索引转移到 GPU。
faiss.IndexFlatL2():创建基于 L2 距离(欧氏距离)的暴力搜索索引,直接计算所有向量间的距离。适用于小规模数据或作为其他索引的量化器。
| 参数 | 类型 | 说明 |
|---|---|---|
d | int | 向量维度(必填)。 |
faiss.index_cpu_to_gpu():将 CPU 上的 Faiss 索引转移到 GPU 上,以加速搜索和训练操作。需先创建 StandardGpuResources 对象
| 参数 | 类型 | 说明 |
|---|---|---|
res | faiss.StandardGpuResources | GPU 资源对象(必填)。 |
device | int | GPU 设备 ID(默认 0)。 |
index | faiss.Index | 要转移的 CPU 索引(必填)。 |
sync | bool | 是否同步 GPU 操作(默认 True)。 |
向量数据库对象(索引).search():在向量数据库(索引)中搜索最相似的 k 个向量。
| 参数 | 类型 | 描述 |
|---|---|---|
xq | np.array | 查询向量(形状 (m, d)) |
k | int | 返回的最近邻数量 |
向量数据库对象(索引).add():向向量数据库(索引)中添加向量数据。
| 参数 | 类型 | 描述 |
|---|---|---|
xb | np.array | 待添加的向量数组(形状 (n, d)) |
np.random.rand():生成指定形状的数组,元素从均匀分布 [0, 1) 中随机采样。
| 参数 | 类型 | 说明 |
|---|---|---|
d0, d1, ..., dn | int, 可选 | 定义输出数组的维度。若无参数,返回单个浮点数。 |
D:Distance 两向量相似度
I:最相似的向量的索引
import faiss
import numpy as npdef test():# 创建标准的 GPU 资源对象,用它来管理GPU相关的计算资源。res = faiss.StandardGpuResources()# 1. 在 CPU 创建索引index_cpu = faiss.IndexFlatL2(256)print(index_cpu)# 2. 将索引转到 GPU# 参数1:GPU 使用资源# 参数2:GPU 设备编号# 参数3:转移的索引index_gpu = faiss.index_cpu_to_gpu(res, 0, index_cpu)print(index_gpu)# 3. 插入数据index_gpu.add(np.random.rand(100000, 256))# 4. 向量搜索D, I = index_gpu.search(np.random.rand(2, 256), k=2)print(D)print(I)if __name__ == '__main__':test()相关文章:

【NLP 76、Faiss 向量数据库】
压抑与痛苦,那些辗转反侧的夜,终会让我们更加强大 —— 25.5.20 Faiss(Facebook AI Similarity Search)是由 Facebook AI 团队开发的一个开源库,用于高效相似性搜索的库,特别适用于大规模向…...

软件名称:系统日志监听工具 v1.0
软件功能:一款基于 PyQt5 开发的 Windows 系统日志监听工具,适用于系统运维、网络管理、故障排查等场景,具备以下核心功能: 支持监听系统三大日志源:应用程序 / 系统 / 安全日志实时抓取新日志事件,自动滚…...
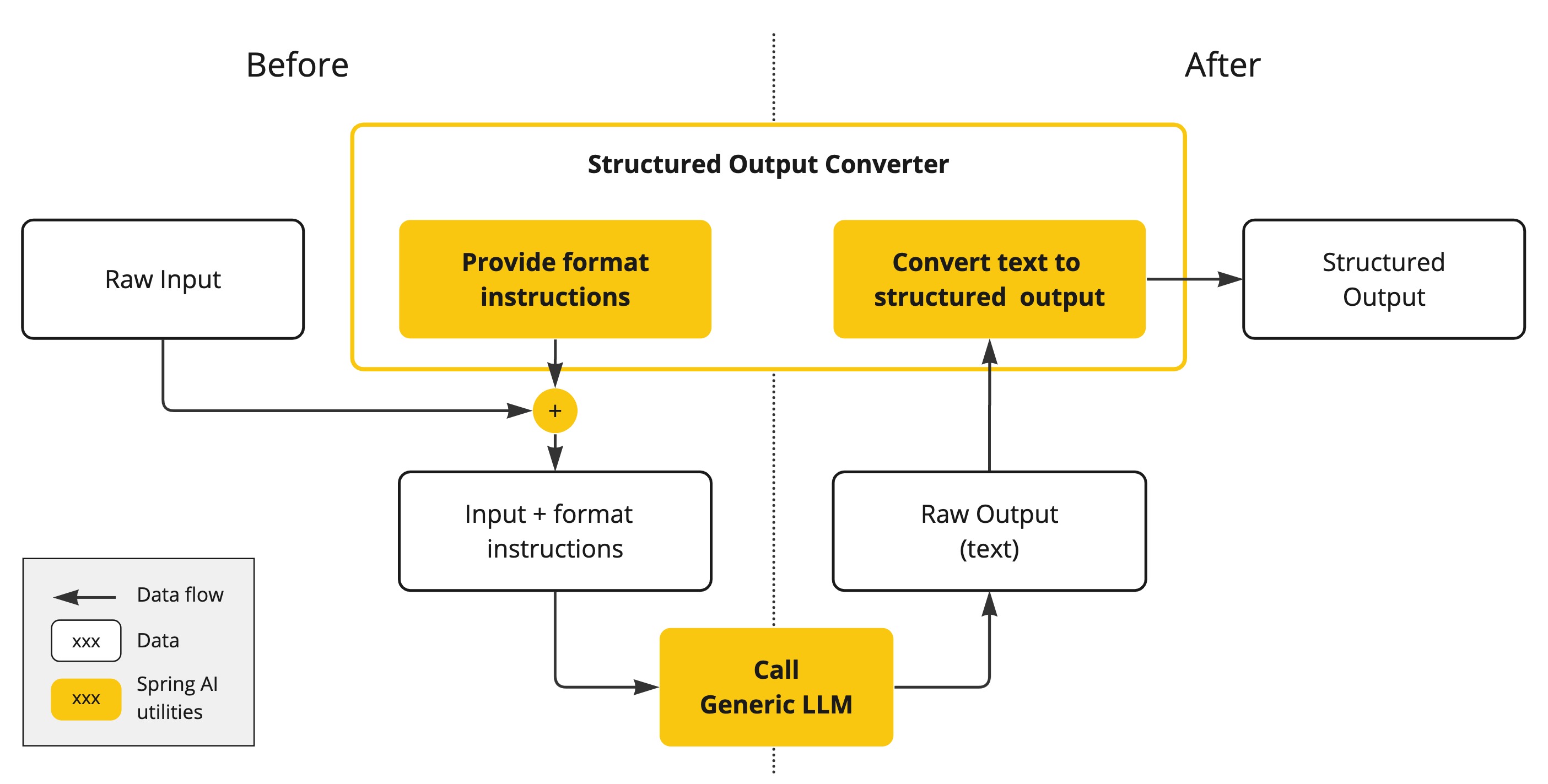
Spring AI 之结构化输出转换器
截至 2024 年 2 月 5 日,旧的 OutputParser、BeanOutputParser、ListOutputParser 和 MapOutputParser 类已被弃用,取而代之的是新的 StructuredOutputConverter、BeanOutputConverter、ListOutputConverter 和 MapOutputConverter 实现类。后者可直接替换前者,并提供相同的…...

Java虚拟机面试题:内存管理(上)
🧑 博主简介:CSDN博客专家,历代文学网(PC端可以访问:https://literature.sinhy.com/#/?__c1000,移动端可微信小程序搜索“历代文学”)总架构师,15年工作经验,精通Java编…...

进程间通信I·匿名管道
目录 进程间通信(IPC) 含义 目的 分类 匿名管道 原理 创建过程 特性 四大情况 close问题 代码练习 简单通信 进程池 小知识 进程间通信(IPC) 含义 就是让不同的进程能看到同一份资源,实现数据交流。 …...

Ubuntu Linux系统的基本命令详情
1.Ubuntu Linux是以桌面应用为主的Linux发行版操作系统 2.Ubuntu的用户使用 在登录系统一般使用在安装系统时建立的普通用户登录,如果要使用超级用户权限 #sudo ---执行命令 sudo passwd ---修改用户密码 su - root ---切换超级用户 系统的不同,命令也不…...

大数据治理:理论、实践与未来展望(二)
书接上文 文章目录 七、大数据治理的未来发展趋势(一)智能化与自动化(二)数据隐私与安全的强化(三)数据治理的云化(四)数据治理的跨行业合作(五)数据治理的生…...

PCB布局设计
PCB布局设计 一、原理图到PCB转换前的准备工作 在将原理图转换为PCB之前,我们需要进行一系列准备工作,确保设计的正确性和完整性。这一步骤至关重要,可以避免后续PCB设计中出现不必要的错误。 // 原理图转PCB前必要检查步骤 // 1. 仔细检查…...

【49. 字母异位词分组】
Leetcode算法练习 笔记记录 49. 字母异位词分组 49. 字母异位词分组 public List<List<String>> groupAnagrams(String[] strs) {Map<String, List<String>> map new HashMap<>();for (int i 0; i < strs.length; i) {//排序就是相同字符了…...

用 AI 让学习更懂你:如何打造自动化个性化学习系统?
用 AI 让学习更懂你:如何打造自动化个性化学习系统? 在这个信息爆炸的时代,传统的学习方式已经难以满足个体化需求。过去,我们依赖固定的教学课程,所有学生按照统一进度进行学习,但每个人的学习节奏、兴趣点和理解方式都不尽相同。而人工智能(AI)正在彻底改变这一局面…...

esp32+IDF V5.1.1版本编译freertos报错
error: portTICK_RATE_MS undeclared (first use in this function); did you mean portTICK_PERIOD_MS 解决方法: 使用命令 idf.py menuconfig 打开配置界面配置freeRtos 使能configENABLE_BACKWARD_COMPATIBLITY...

嵌入式软件-如何做好一份技术文档?
嵌入式软件-如何做好一份技术文档? 文章目录 嵌入式软件-如何做好一份技术文档?一.技术文档的核心价值与挑战二.文档体系的结构化设计三.精准表达嵌入式特有概念四. **像管理代码一样管理文档**,代码与文档的协同维护五.质量评估与持续改进5.…...

笔记本6GB本地可跑的图生视频项目(FramePack)
文章目录 (一)简介(二)本地执行(2.1)下载(2.2)更新(2.3)运行(2.4)生成 (三)注意(3.1)效…...

SpringMVC实战:动态时钟
引言 在现代 Web 开发中,选择一个合适的框架对于项目的成功至关重要。Spring MVC 作为 Spring 框架的核心模块之一,以其清晰的架构、强大的功能和高度的可配置性,成为了 Java Web 开发领域的主流选择。本文将通过一个“动态时钟”的实战项目…...

vscode include总是报错
VSCode 的 C/C 扩展可以通过配置 c_cpp_properties.json 来使用 compile_commands.json 文件中的编译信息,包括 include path、编译选项等。这样可以确保 VSCode 的 IntelliSense 与实际编译环境保持一致。 方法一:直接指定 compile_commands.json 路径…...

哈希表的实现(上)
前言 在C98中,STL提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到,即最差情况下需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好的查询是,进行很少的比较次数就能够将…...

【Java高阶面经:微服务篇】1.微服务架构核心:服务注册与发现之AP vs CP选型全攻略
一、CAP理论在服务注册与发现中的落地实践 1.1 CAP三要素的技术权衡 要素AP模型实现CP模型实现一致性最终一致性(Eureka通过异步复制实现)强一致性(ZooKeeper通过ZAB协议保证)可用性服务节点可独立响应(支持分区存活)分区期间无法保证写操作(需多数节点可用)分区容错性…...

实验7 HTTP协议分析与测量
实验7 HTTP协议分析与测量 1、实验目的 了解HTTP协议及其报文结构 了解HTTP操作过程:TCP三次握手、请求和响应交互 掌握基于tcpdump和wireshark软件进行HTTP数据包抓取和分析技术 2、实验环境 硬件要求:阿里云云主机ECS 一台。 软件要求࿱…...

python:机器学习概述
本文目录: 一、人工智能三大概念二、学习方式三、人工智能发展史**1950-1970****1980-2000****2010-2017****2017-至今** 四、机器学习三要素五、常见术语六、数据集的划分七、常见算法分类八、机器学习的建模流程九、特征工程特征工程包括**五大步**:特…...

【一. Java基础:注释、变量与数据类型详解】
1. Java 基础概念 1.1 注释 注释:对代码的解释和说明文字 java的三种注释: 单行注释:两个斜杠 // 后面跟着你的注释内容 //哈哈多行注释:以 /* 开头,以 */ 结尾,中间可以写很多行 /*哈哈哈哈哈哈…...

得力DE-620K针式打印机打印速度不能调节维修一例
基本参数: 产品类型 票据针式打印机(平推式) 打印方式 串行点阵击打式 打印宽度 85列 打印针数 24针 可靠性 4亿次/针 色带性能 1000万字符纠错 复写能力 7份(1份原件+6份拷贝) 缓冲区 128KB 接口类型 …...

SAP在金属行业的数字化转型:无锡哲讯科技的智能解决方案
金属行业面临的发展挑战 金属行业作为制造业的基础支柱,涵盖钢铁、有色金属、金属制品等多个细分领域。当前行业正面临原材料价格波动、能耗双控政策、市场竞争加剧等多重压力。数字化转型已成为金属企业提升生产效率、优化供应链、实现绿色可持续发展的必由之路。…...

安装openresty使用nginx+lua,openresty使用jwt解密
yum install -y epel-release yum update yum search openresty # 查看是否有可用包 yum install -y openresty启动systemctl start openresty验证服务状态systemctl status openresty设置开机自启systemctl enable openrestysystemctl stop openresty # 停止服务 system…...

java基础(继承)
什么是继承 继承好处 提高代码的复用性 继承注意事项 权限修饰符 单继承、Object类 冲突: 方法重写 扩展: 其实我们不想看地址,地址看来没用,我们是用来看对象有没有问题 重写toString: 比如这个如果返回的是地址值,…...

python 实现一个完整的基于Python的多视角三维重建系统,包含特征提取与匹配、相机位姿估计、三维重建、优化和可视化等功能
多视角三维重建系统 下面我将实现一个完整的基于Python的多视角三维重建系统,包含特征提取与匹配、相机位姿估计、三维重建、优化和可视化等功能。 1. 环境准备与数据加载 首先安装必要的库: pip install opencv-python opencv-contrib-python numpy…...

行列式中某一行的元素与另一行对应元素的代数余子式乘积之和等于零
问题陈述 为什么行列式中某一行(列)的元素与另一行(列)对应元素的代数余子式乘积之和等于零?即: ∑ k 1 n a i k C j k 0 ( i ≠ j ) \sum_{k1}^{n} a_{ik} C_{jk} 0 \quad (i \ne j) k1∑naikCjk…...

【时时三省】Python 语言----字符串,列表,元组,字典常用操作异同点
目录 1,字符串常用操作 1,创建 2,访问 3,常用方法 4,内置方法 2,列表 1,创建列表 2,访问列表 3,内置方法 3,元组 1,创建 2,访问 3,内置方法 4,字典 1,创建 2,访问 3,内置方法 5,集合 1,创建 2,访问 3,内置方法 山不在高,有仙则名。水不在深,有龙则…...

基于cornerstone3D的dicom影像浏览器 第二十二章 mpr + vr
系列文章目录 第一章 下载源码 运行cornerstone3D example 第二章 修改示例crosshairs的图像源 第三章 vitevue3cornerstonejs项目创建 第四章 加载本地文件夹中的dicom文件并归档 第五章 dicom文件生成png,显示检查栏,序列栏 第六章 stack viewport 显…...

优启通添加自定义浏览器及EXLOAD使用技巧分享
文章目录 优启通添加自定义浏览器及EXLOAD使用技巧分享🚩问题描述🔧解决方案概述📁自定义软件添加方法汇总🧩快捷方式配置:exload.cfg 用法大全🧷基础用法🗂分类菜单🖥创建桌面快捷方…...

MySQL:游标 cursor 句柄
当我们select * from emp 可以查看所有的数据 这个数据就相当于一个数据表 游标的作用相当于一个索引 一个指针 指向每一个数据 假设说我要取出员工中薪资最高的前五名成员 就要用到limit关键字 但是这样太麻烦了 所以这里用到了游标 游标的声明: declare my…...
