【c++】【数据结构】AVL树
目录
- AVL树的定义
- AVL树的部分模拟实现
- 平衡因子的引入
- 平衡因子的向上调整
- 旋转算法
- 单旋算法
- 右单旋
- 左单旋
- 双旋算法
- 左右双旋
- 右左双旋
AVL树的定义
AVL树本质是一种搜索二叉树,传统的二叉搜索树我们都有所了解,其在理想情况下也就是接近满二叉树时拥有极高的插入与搜索效率,但是极其的不稳定。AVL树就是针对这种问题而产生的,其名字来源于发明创造他的科学家。AVL树是一种自平衡的二叉搜索树,拥有特定的算法动态维持平衡,避免因插入不平衡而产生的插入搜索效率低下的问题。
AVL树的部分模拟实现
#pragma once#include<iostream>#include<algorithm>using namespace std;template<class Key, class Value>
struct AVL_Node
{typedef AVL_Node<Key, Value> Node;AVL_Node(Key k, Value v):_key(k),_value(v){}Node* _parent = nullptr;Node* _left = nullptr;Node* _right = nullptr;Key _key = 0;Value _value = 0;int BFactor = 0;//平衡因子
};template<class Key, class Value>
class AVL
{
public:typedef AVL_Node<Key, Value> Node;bool find(Key a){return _find(root, a);}bool insert(Key a, Value b){if (!root)//树判空{root = new Node(a, b);return true;}Node* cur = root;Node* parent = nullptr;while (cur)//找位置{if (cur->_key == a) return false;parent = cur;if (cur->_key > a) cur = cur->_left;else cur = cur->_right;}if (parent->_key > a)//插入{parent->_left = new Node(a, b);cur = parent->_left;cur->_parent = parent;//parent->BFactor++;}else{parent->_right = new Node(a, b);cur = parent->_right;cur->_parent = parent;//parent->BFactor--;}Node* son = nullptr;while (parent){if (parent->_key > cur->_key){parent->BFactor++;}else{parent->BFactor--;}if (parent->BFactor == 0) break;if (parent->BFactor == 2 || parent->BFactor == -2){if (parent->_key > cur->_key){if (son && (cur->_key > son->_key)) Rrotation(cur);else LRrotation(cur);}else{if (son && (cur->_key < son->_key)) Lrotation(cur);else RLrotation(cur);}break;}son = cur;cur = parent;parent = parent->_parent;}return true;}void inorder()//中序打印{_inorder(root);}int high()//树的高度{return high(root);}void check()//检查结点平衡{_check(root);}private:void _check(Node* cur){if (!cur) return;if (high(cur->_left) - high(cur->_right) != cur->BFactor){cout << cur->_key << " : " << cur->BFactor << ", " << high(cur->_left) - high(cur->_right) << endl;}check(cur->_left);check(cur->_right);}int _high(Node* cur){if (!cur) return 0;int releft = high(cur->_left);int reright = high(cur->_right);return releft > reright ? releft + 1 : reright + 1;}void _inorder(Node* cur){if (!cur) return;_inorder(cur->_left);cout << cur->_key << endl;_inorder(cur->_right);}void LRrotation(Node* cur){if (cur->_right->BFactor == 1){Lrotation(cur->_right);cur = cur->_parent;Rrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 0;cur->_right->BFactor = -1;}else if (cur->_right->BFactor == -1){Lrotation(cur->_right);cur = cur->_parent;Rrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 1;cur->_right->BFactor = 0;}else //cur的子结点是刚插入的情况{Lrotation(cur->_right);cur = cur->_parent;Rrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 0;cur->_right->BFactor = 0;}}void RLrotation(Node* cur){if (cur->_left->BFactor == 1){Rrotation(cur->_left);cur = cur->_parent;Lrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 0;cur->_right->BFactor = -1;}else if (cur->_left->BFactor == -1){Rrotation(cur->_left);cur = cur->_parent;Lrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 1;cur->_right->BFactor = 0;}else //cur的子结点是刚插入的情况{Rrotation(cur->_left);cur = cur->_parent;Lrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 0;cur->_right->BFactor = 0;}}void Lrotation(Node* cur){Node* parent = cur->_parent;Node* pparent = parent->_parent;Node* cur_left = cur->_left;parent->_right = cur_left; //左右节点更新cur->_left = parent;if(cur_left) cur_left->_parent = parent; //父节点的更新parent->_parent = cur;cur->_parent = pparent;if (pparent) //判断是不是空{if (pparent->_key > cur->_key) pparent->_left = cur; //父节点的父节点更新else pparent->_right = cur;}else{root = cur;cur->_parent = nullptr; //解耦}cur->BFactor = 0; //平衡因子的更新parent->BFactor = 0;}void Rrotation(Node* cur){Node* parent = cur->_parent;Node* pparent = parent->_parent;//Node* son = cur->_left;Node* cur_right = cur->_right;parent->_left = cur_right; //左右节点更新cur->_right = parent;if (cur_right) cur_right->_parent = parent; //父节点的更新parent->_parent = cur;cur->_parent = pparent;if (pparent) //判断是不是空{if (pparent->_key > cur->_key) pparent->_left = cur; //父节点的父节点更新else pparent->_right = cur;}else{root = cur;cur->_parent = nullptr; //解耦}cur->BFactor = 0; //平衡因子的更新parent->BFactor = 0;}bool _find(Node* root, Key a){if (!root) return false;if (root->_key == a) return true;if (root->_key > a) return _find(root->_left, a);return _find(root->_right, a);}Node* root = nullptr;
};
AVL树是相对复杂的数据结构,它的核心算法是插入和删除函数,删除函数比起插入函数还要再难上一点,笔者能力有限,只对插入函数进行了实现。
平衡因子的引入
对于AVL树,首先我们还是要明确,其本质还是一颗二叉搜索树,所以先是要对其结点类进行定义。这里笔者采用的还是经典的Key-Value模型,抛开普通二叉搜索树所有的成员变量之外,笔者还定义了一个平衡因子,这是AVL树的关键。前面我们也说过,AVL树是一个自平衡的二叉搜索树,在弄清楚平衡是如何保持的之前,我们先应该明白AVL如何定义平衡与不平衡的。对于平衡二叉树来说,其最理想的状态无疑是满二叉树的状态,但是满二叉树不是想有就有的,只有特定的结点数量才能有满二叉树,很多情况下我们只能追求类似完全二叉树的状态也就是确保倒数第二层全满,而最后一层没满的情况。所以对于平衡状态的定义我们不应该过于严格,AVL树将每一个结点的左右子树的高度差不超过1的情况定义为平衡状态,反之就是不平衡状态。因此,我们可以在每个结点中都引入一个平衡因子,当然也有一些AVL树的实现是没有定义平衡因子的,那样的话就需要通过其他的方式得出左右子树的高度差,不过平衡因子这样的方式很方便,有很多人用。在每一个AVL树的结点中的平衡因子只有三种可能值:0,1,-1。用来表示左右子树相等,左子树的高度比右子树的高度大1,右子树的高度比左子树的高度大1这三种情况。如果出现2,-2这两种情况就要使用算法及时维护,保持平衡因子在正常范围内。
平衡因子的向上调整
AVL树的结点插入部分与普通二叉搜索树一样,但是在插入之后需要对平衡因子进行更新,如何更新呢?先来看一下这两种情况,


对于结点的插入,大致可以分为以上这两种,即对一个叶子结点插入的情况和对于一个有子结点的结点插入的情况。对于第一种情况,其在插入之后对于其父结点的平衡因子毫无疑问是要进行更新的,但我们要考虑的不仅仅是这个父结点,还有父结点的一系列祖宗结点,即从父结点出发向上直到根节点的路径上的所有节点,因为结点的插入会影响树的高度,进而会影响所有的祖宗结点,其他节点则不会受影响。说白了,平衡因子是左右子树之差,所以能影响它的只有子树高度的改变,子树没有插入结点,子树高度就不会变,平衡因子也就不会改变。那么这里究竟会不会呢?答案是不会的,虽然插入了结点,但是这颗子树的高度没有改变,还是2,高度没有变化也就不会影响它的祖宗节点。对于第二种情况呢?答案是会的,因为这种插入方式改变了树的高度,即将树的高度由1变成了2,这时高度的改变势必会影响它的祖宗结点。所以我们应该继续向上调整父节点的父节点,为了方便向上调整,结点中也引入了父结点的指针。那么究竟如何调整呢?我们再看向下面三张图,



在不考虑左右结点搭配的情况下,结点更新时就会遇到这三种情况,第一种情况树的高度没有发生变化,所以就不用再向上调整了;第二种树的高度发生了改变,还需要再次调整;第三种情况不仅树的高度发生了变化,两树高度之差还超过了1,需要算法来调整。看完了这么多种情况,我们会发现情况真的很多很复杂,如何总结并转换成代码呢?首先我们明白,当树的高度不再发生变化时,平衡因子的向上调整就该结束了,如何判断这种情况呢?我们发现,由于二叉树只有两棵子树,且AVL树的结点左右子树高度差不超过1,所以树的高度不发生变化的情况只有结点的左右子树高度差正好由1或-1变成0时,树的高度不会发生变化,平衡因子的向上调整在此终止。当AVL树的结点的左右子树高度差由0变成1或者-1时,树的高度会发生变化,平衡因子需要继续向向上调整。当AVL树的结点的左右子树高度差由1或者-1变成2或者-2时,树的平衡已经被破坏了,需要动用算法来维护了,算法我们之后说。总结一下就是父节点的平衡因子改变后是0就结束,是1或-1就继续向上调整,是2或-2就动用算法。至此,我们就完成了AVL树插入函数的大框架,
bool insert(Key a, Value b)
{if (!root)//树判空{root = new Node(a, b);return true;}Node* cur = root;Node* parent = nullptr;while (cur)//找位置{if (cur->_key == a) return false;parent = cur;if (cur->_key > a) cur = cur->_left;else cur = cur->_right;}if (parent->_key > a)//插入{parent->_left = new Node(a, b);cur = parent->_left;cur->_parent = parent;//parent->BFactor++;}else{parent->_right = new Node(a, b);cur = parent->_right;cur->_parent = parent;//parent->BFactor--;}Node* son = nullptr;while (parent){if (parent->_key > cur->_key){parent->BFactor++;}else{parent->BFactor--;}if (parent->BFactor == 0) break;if (parent->BFactor == 2 || parent->BFactor == -2){// 平衡因子维护算法}son = cur;cur = parent;parent = parent->_parent;}return true;
}
首先我们先对树进行判空,如果树为空,那最简单了,直接将要插入的结点设为根结点返回就行了。树不为空的话,我们就要先找到要插入的位置插入。之后进入循环,对父结点的平衡因子进行更新,插入的是左结点的就对父结点++,插入的是右结点的话就对父结点–。之后根据更新后的父结点的平衡因子的值进行相应操作,如果是1或-1,就将cur指针指向父结点,进入下一个循环对父结点的父结点再次重复相应的操作,是0就结束循环,是2或-2就用算法。这样,剩下的就只有算法了,这也是最难的一部分。
旋转算法
单旋算法
首先我们应该明确,在AVL树中,平衡因子最多也就是2或-2,是不会有3或-3,4或-4这种情况的,因为在插入时遇到平衡因子变成2或-2时就会及时调用算法调整,如果出现了大于2或小于-2的情况,就是自己写错了,在平衡因子为2或-2时没有调整。所以,我们在思考不平衡的情况时只要考虑左右子树之差为2或-2的情况就行。
右单旋
我们看向下面这一张图,

这就是一张典型的不平衡的AVL树,因为其根结点的左子树高度为2,右子树的高度为0,左右子树高度之差为2。那么其实这张图就可以变成,

这张图的h为0时就等于上面这张图,它代表的不只是一张图,是一种情况,比起第一张图,它更具有普适性,对于这种树不平衡的情况,就要使用旋转函数的单旋函数中的右单旋了。
说是旋转函数,到底应该怎么做呢?笔者做了下面这张图,

这种因为左子树过高将父结点向下压达到左右平衡的效果,就像整个树向右旋转了一样,这种做法叫做右单旋。右单旋的实现函数如下,
void Rrotation(Node* cur)
{Node* parent = cur->_parent;Node* pparent = parent->_parent;//Node* son = cur->_left;Node* cur_right = cur->_right;parent->_left = cur_right; //左右节点更新cur->_right = parent;if (cur_right) cur_right->_parent = parent; //父节点的更新parent->_parent = cur;cur->_parent = pparent;if (pparent) //判断是不是空{if (pparent->_key > cur->_key) pparent->_left = cur; //父节点的父节点更新else pparent->_right = cur;}else{root = cur;cur->_parent = nullptr; //解耦}cur->BFactor = 0; //平衡因子的更新parent->BFactor = 0;
}
根据传过来的cur指针算出cur的父结点的指针,爷爷结点的指针以及cur的右子节点的指针,这样我们就把右单旋指针对接所涉及的结点地址都记录下来了,对接时就不用担心指针覆盖的问题了。之后我们将cur的父结点的左指向cur的右子节点,cur的右指向cur的父结点。左右结点指针更新之后,别忘了还有为了方便向上调整而引入到结点中的父结点指针。首先我们先对cur的右子结点指针判空,cur的右子结点是有可能为空的,但是为空时将cur的父结点的左指向它不会有问题,因为本来就应该指向空,而父结点的指针更新就不行了,我们应该先判空,不为空的话就将他的父结点指针指向cur的父结点。然后再将cur的父结点的父结点指针指向cur,cur的父结点指针指向爷爷结点。最后我们还应注意cur的父结点是根结点的情况,因为根结点是没有父结点的,换到这里就是没有爷爷结点。如果有爷爷结点,就将爷爷结点的左或右子结点的指针指向cur。如果没有,先将cur的父结点指针置空,再将AVL树的根结点更新为cur。之后是对平衡因子的更新,其实将平衡因子的更新与旋转函数解耦更好,笔者这里怕麻烦没改了。通过这两个平衡因子的更新我们会发现,旋转后的cur与parent结点的平衡因子都变成了0,当然原本parent的位置上现在是cur了,但平衡因子为0意味着不用向上更新了,可以直接结束循环。
左单旋
听名字就知道,左单旋就是右单旋的完全镜像版,旋转过程与算法书写原理也是一模一样,笔者直接放出代码,不做过多赘述。
void Lrotation(Node* cur)
{Node* parent = cur->_parent;Node* pparent = parent->_parent;Node* cur_left = cur->_left;parent->_right = cur_left; //左右节点更新cur->_left = parent;if(cur_left) cur_left->_parent = parent; //父节点的更新parent->_parent = cur;cur->_parent = pparent;if (pparent) //判断是不是空{if (pparent->_key > cur->_key) pparent->_left = cur; //父节点的父节点更新else pparent->_right = cur;}else{root = cur;cur->_parent = nullptr; //解耦}cur->BFactor = 0; //平衡因子的更新parent->BFactor = 0;
}
双旋算法
在AVL树中,单单使用单旋算法是不能够应对所有情况的,对于一下两种情况,


使用单旋算法无法完成平衡,我们看一下,如果对其使用单旋会发生什么,

我们会发现当我们对左子树高的情况使用右旋时,最后变成了右子树高的情况,AVL树还是不平衡。怎么办呢?这时就要用到双旋了。
左右双旋
对于左子树高且呈折现形的情况,

旋转一次无法解决问题,我们应该先来一个左单旋,再来一个右单旋,

通过这样的方式可以实现树的平衡,在实际书写时我们也可以复用我们之前写好的左右单旋函数,但是,有一点不一样的是,平衡因子的更新,我们可以看到,实际双旋完这三个结点的平衡因子并不都是0,这里是存在俩各种情况的,我们需要分情况处理。
实际旋转完平衡因子的更新与son结点的哪棵子树更高有关系,


当然,我们还应该考虑son就是新插入的结点的情况,

我们在插入之前就对son结点的三种情况进行判断,在双旋结束之后更新对应的平衡因子就行。
void LRrotation(Node* cur)
{if (cur->_right->BFactor == 1){Lrotation(cur->_right);cur = cur->_parent;Rrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 0;cur->_right->BFactor = -1;}else if (cur->_right->BFactor == -1){Lrotation(cur->_right);cur = cur->_parent;Rrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 1;cur->_right->BFactor = 0;}else //cur的子结点是刚插入的情况{Lrotation(cur->_right);cur = cur->_parent;Rrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 0;cur->_right->BFactor = 0;}
}
这里需要注意,在第一次旋转之后,cur与son的位置已经乱了,需要将旋转完的son视为新的cur进行第二次旋转。son是刚插入的情况三个节点的平衡因子都是0,son的左子树高的情况需要将最后son(重置完是cur)的右结点的平衡因子更新为-1,son的右子树高的情况需要将最后son的左结点的平衡因子更新为1。
右左双旋
与左右单旋同理,右左双旋也是左右双旋的完全镜像版,算法书写原理一模一样,这里不过多赘述,直接放代码。
void RLrotation(Node* cur)
{if (cur->_left->BFactor == 1){Rrotation(cur->_left);cur = cur->_parent;Lrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 0;cur->_right->BFactor = -1;}else if (cur->_left->BFactor == -1){Rrotation(cur->_left);cur = cur->_parent;Lrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 1;cur->_right->BFactor = 0;}else //cur的子结点是刚插入的情况{Rrotation(cur->_left);cur = cur->_parent;Lrotation(cur);cur->BFactor = 0;cur->_left->BFactor = 0;cur->_right->BFactor = 0;}
}
至此,插入函数的旋转算法全部讲完了,我们将对应的情况与对应的算法写入插入函数,
bool insert(Key a, Value b)
{if (!root)//树判空{root = new Node(a, b);return true;}Node* cur = root;Node* parent = nullptr;while (cur)//找位置{if (cur->_key == a) return false;parent = cur;if (cur->_key > a) cur = cur->_left;else cur = cur->_right;}if (parent->_key > a)//插入{parent->_left = new Node(a, b);cur = parent->_left;cur->_parent = parent;//parent->BFactor++;}else{parent->_right = new Node(a, b);cur = parent->_right;cur->_parent = parent;//parent->BFactor--;}Node* son = nullptr;while (parent){if (parent->_key > cur->_key){parent->BFactor++;}else{parent->BFactor--;}if (parent->BFactor == 0) break;if (parent->BFactor == 2 || parent->BFactor == -2){if (parent->_key > cur->_key){if (son && (cur->_key > son->_key)) Rrotation(cur);else LRrotation(cur);}else{if (son && (cur->_key < son->_key)) Lrotation(cur);else RLrotation(cur);}break;}son = cur;cur = parent;parent = parent->_parent;}return true;
}
就这样,AVL的核心之一——插入函数就完成了。除了插入函数之外,我还写了查找函数等的一些函数来检测插入函数正确与否,大家可以用作参考,实现思路都很简单,不过多赘述。
相关文章:

【c++】【数据结构】AVL树
目录 AVL树的定义AVL树的部分模拟实现平衡因子的引入平衡因子的向上调整旋转算法单旋算法右单旋左单旋 双旋算法左右双旋右左双旋 AVL树的定义 AVL树本质是一种搜索二叉树,传统的二叉搜索树我们都有所了解,其在理想情况下也就是接近满二叉树时拥有极高的…...

【原神 × 插入排序】刷圣遗物也讲算法:圣遗物评分系统背后的排序逻辑你真的懂吗?
📘 改编自:王争《数据结构与算法之美》 🎮 游戏演绎:米哈游《原神》 🧠 核心关键词:插入排序、排序算法、评分系统、属性评价、强化圣遗物、冒泡排序对比 🧭 引言:原神刷本=刷排序? 玩《原神》的玩家每天日常是啥?体力用来刷圣遗物、精通头、暴击头、攻充沙………...

ORB-SLAM2学习笔记:ExtractorNode::DivideNode和ORBextractor::DistributeOctTree函数详解
一、ExtractorNode::DivideNode void ExtractorNode::DivideNode(ExtractorNode &n1, ExtractorNode &n2, ExtractorNode &n3, ExtractorNode &n4) {const int halfX = ceil(static_cast<float>(UR.x-UL.x)/2);const int halfY = ceil(static_cast<f…...

nt!MmMapViewInSystemCache函数分析PointerPte的填充
第一部分: 1: kd> kc # 00 nt!MmMapViewInSystemCache 01 nt!CcGetVacbMiss 02 nt!CcGetVirtualAddress 03 nt!CcMapData 04 Ntfs!NtfsMapStream 05 Ntfs!NtfsReadBootSector 06 Ntfs!NtfsMountVolume 07 Ntfs!NtfsCommonFileSystemControl 08 Ntfs!NtfsFspDis…...
)
3D Tiles高级样式设置与条件渲染(3)
二、基于地理距离的条件渲染 1.根据与特定点的距离设置样式 在某些应用中,我们可能需要根据建筑物与某个特定点(如地标建筑)的距离来设置样式。以下代码示例展示了如何根据建筑物与广州塔的距离来设置颜色和可见性: tiles3d.styl…...

通义灵码深度实战测评:从零构建智能家居控制中枢,体验AI编程新范式
一、项目背景:零基础挑战全栈智能家居系统 目标:开发具备设备控制、环境感知、用户习惯学习的智能家居控制中枢(PythonFlaskMQTTReact) 挑战点: 需集成硬件通信(MQTT)、Web服务(Flask)、前端交互(React) 调用天气AP…...

头歌之动手学人工智能-Pytorch 之优化
目录 第1关:如何使用optimizer 任务描述 编程要求 测试说明 真正的科学家应当是个幻想家;谁不是幻想家,谁就只能把自己称为实践家。 —— 巴尔扎克开始你的任务吧,祝你成功! 第2关:optim.SGD 任务描述…...

基于谷歌ADK的智能客服系统简介
Google的智能体开发工具包(Agent Development Kit,简称ADK)是一个开源的、以代码为中心的Python工具包,旨在帮助开发者更轻松、更灵活地构建、评估和部署复杂的人工智能智能体(AI Agent)。ADK 是一个灵活的…...

(一)视觉——工业相机(以海康威视为例)
一、工业相机介绍 工业相机是机器视觉系统中的一个关键组件,其最本质的功能就是将光信号转变成有序的电信号。选择合适的相机也是机器视觉系统设计中的重要环节,相机的选择不仅直接决定所采集到的图像分辨率、图像质量等,同时也与整个系统的运…...

DAY 36 超大力王爱学Python
仔细回顾一下神经网络到目前的内容,没跟上进度的同学补一下进度。 作业:对之前的信贷项目,利用神经网络训练下,尝试用到目前的知识点让代码更加规范和美观。探索性作业(随意完成):尝试进入nn.Mo…...

基于React + TypeScript构建高度可定制的QR码生成器
前言 在现代Web应用中,QR码已成为连接线上线下的重要桥梁。本文将详细介绍如何使用React TypeScript Vite构建一个功能强大、高度可定制的QR码生成器,支持背景图片、文本叠加、HTML模块、圆角导出等高级功能。 前往试试 项目概述 技术栈 前端框架:…...

DeepSeek进阶教程:实时数据分析与自动化决策系统
进阶教程:实时数据分析与自动化决策系统 1. 实时数据流处理架构 class StreamProcessor:def __init__(self):self.window_size = 60 # 滑动窗口大小(秒)self.analytics_engine = AnalyticsEngine() # 复用之前的分析引擎def process_kafka_stream(self, topic):"&quo…...

visual studio 2022 初学流程
本文采用总-分的形式讲述流程 1.前端外部可以使用的接口 ExternalDataWebService.asmx?opReportWaterForWayder 新建ExternalDataWebService.asmx 文件 <% WebService Language"C#" CodeBehind"~/App_Code/ExternalDataWebService.cs" Class…...

SRD-12VDC-SL-C 继电器接线图解
这个继电器可以使用12伏的直流电源控制250伏和125伏的交流电,也可以控制30伏和28伏的直流电,电流都为10安。 此继电器有5个引脚,各个的作用如下: 引脚4和引脚5为触点, 引脚1和引脚3为线圈引脚,接12伏的直…...

基于开源链动2+1模式AI智能名片S2B2C商城小程序的企业组织生态化重构研究
摘要:本文以互联网时代企业组织结构变革为背景,探讨开源链动21模式AI智能名片S2B2C商城小程序在推动企业从封闭式向开放式生态转型中的核心作用。通过分析传统企业资源获取模式与网络化组织生态的差异,结合开源链动21模式的裂变机制、AI智能名…...

前端面经 两栏布局
两栏布局 float实现 1.给父盒子加float:hidden实现BFC 2.给左盒子加浮动float:left 给宽度 flex布局 1父盒子 display:flex 2左盒子 固定宽度 3.右盒子 flex:1 三栏布局 法1:浮动实现 1 父盒子overflow:hidden 实现BFC 2左盒子:float:left 3右盒子 :floa…...

2,QT-Creator工具创建新项目教程
目录 1,创建一个新项目 demo_01.pro(项目配置文件) 类似 CMakeList.txt widget.h(头文件) main.cpp(程序入口) widget.cpp(源文件) widget.ui(界面设计文件) 1,创建一个新项目 依次选择: 设置路径: 选择编译器: 如果选择CMake, 就会生成cmakel…...

《深入解析SPI协议及其FPGA高效实现》-- 第一篇:SPI协议基础与工作机制
第一篇:SPI协议基础与工作机制 1. 串行外设接口导论 1.1 SPI的核心定位 协议本质 : 全双工同步串行协议(对比UART异步、IC半双工)核心优势 : 无寻址开销(通过片选直连)时钟速率可达100MHz&…...

2025年5月6日 飞猪Java一面
锐评 鸡蛋鸭蛋荷包蛋 我的蛋仔什么时候才能上巅峰凤凰蛋? 1. 如何保证数据库数据和redis数据一致性 数据库数据和 redis 数据不一致是在 高并发场景下更新数据的情况 首先我们要根据当前保持数据一致性的策略来决定方案 如果采取的策略是先删除缓存 更新数据库 我们假设现…...

技术深度解析:《鸿蒙5.0+:AI驱动的全场景功耗革命》
引言:鸿蒙5.0的能效革新目标 行业挑战: 移动设备多设备协同需求激增,传统系统面临分布式通信开销、AI算力碎片化、边缘设备能效瓶颈等问题。鸿蒙5.0突破: 引入方舟引擎3.0(ArkTS编译优化…...

Nodejs+http-server 使用 http-server 快速搭建本地图片访问服务
在开发过程中,我们经常需要临时查看或分享本地的图片资源,比如设计稿、截图、素材等。虽然可以通过压缩发送,但效率不高。本文将教你使用 Node.js 的一个轻量级工具 —— http-server,快速搭建一个本地 HTTP 图片预览服务…...

Zsh/Bash Conda设置延迟启动,启动速度优化
Zsh/Bash 启动速度优化 在安装完 Conda 之后,会发现每次启动 Zsh/Bash 的时候都需要加载时间,这个时候就会发现没有以前流畅了,原因是因为每次启动 Shell 时都需要去加载 Conda 环境,才能保证每次可以使用工具。然而官方自带的安…...

【AI论文】推理语言模型的强化学习熵机制
摘要:本文旨在克服将强化学习扩展到使用 LLM 进行推理的主要障碍,即策略熵的崩溃。 这种现象在没有熵干预的RL运行中一直存在,其中策略熵在早期训练阶段急剧下降,这种探索能力的减弱总是伴随着策略性能的饱和。 在实践中ÿ…...

Java中的JSONObject详解:从基础到高级应用
Java中的JSONObject详解:从基础到高级应用 在当今前后端分离的架构中,JSONObject已成为Java开发者处理JSON数据的瑞士军刀。本文将深入解析JSONObject的核心机制与实战技巧。 一、JSONObject的本质与实现库 1.1 核心定位 JSONObject是Java中表示JSON对…...
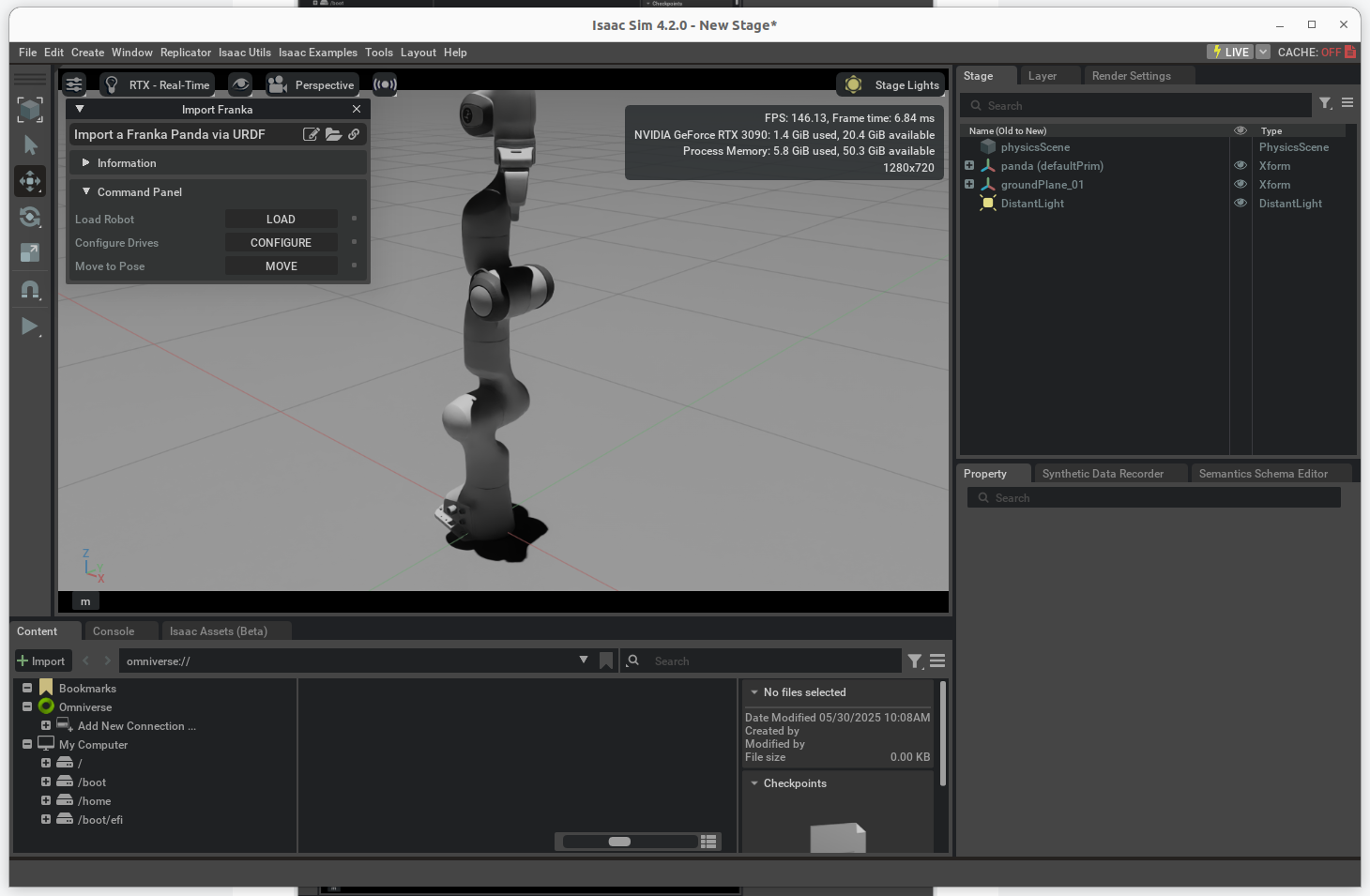
Ubuntu22.04 安装 IsaacSim 4.2.0
1. 从官网下载 IsaacSim 4.2.0 安装包 https://download.isaacsim.omniverse.nvidia.com/isaac-sim-standalone%404.2.0-rc.18%2Brelease.16044.3b2ed111.gl.linux-x86_64.release.zip 2. 查阅 Workstation Installation 安装方式 Workstation Installation — Isaac Sim Do…...

子串题解——和为 K 的子数组【LeetCode】
谨记: 数组不是单调的话,不要用滑动窗口,考虑用前缀和 写法一:两次遍历 代码的核心思想是通过 前缀和 和 哈希表 来高效地统计符合条件的子数组个数。具体步骤如下: 计算前缀和数组 s: s[i] 表示 nums 的前…...

深入理解设计模式之访问者模式
深入理解设计模式之访问者模式(Visitor Pattern) 一、什么是访问者模式? 访问者模式(Visitor Pattern)是一种行为型设计模式。它的主要作用是将数据结构与数据操作分离,使得在不改变数据结构的前提下&…...

Java代码重构:如何提升项目的可维护性和扩展性?
Java代码重构:如何提升项目的可维护性和扩展性? 在Java开发领域,随着项目规模的不断扩大和业务需求的频繁变更,代码的可维护性和扩展性逐渐成为了项目成功的关键因素。代码重构作为一种优化代码质量的重要手段,能够在…...

《Python语言程序设计》2018 第4章第9题3重量和价钱的对比,利用第7章的概念来解答你
利用类来解答这个问题。 pack1, price1 50, 24.59 pack2, price2 25, 11.99class result:def __init__(self,pack,price):self.pack packself.price pricedef set_pack(self):return self.packdef set_price(self):return self.pricedef get_result(self):return self.pric…...

Nginx安装操作命令
Nginx官网:https://nginx.org/ Nginx下载地址:http://nginx.org/en/download.html # 重载nginx服务 systemctl reload nginx # 启动nginx服务 systemctl start nginx # 关闭nginx服务 systemctl stop nginx # 设置nginx服务开机自启动 systemctl enable…...
