【深度学习】 19. 生成模型:Diffusion Models
Diffusion Models
Diffusion Models 简介
Diffusion 模型是一类通过逐步添加噪声并再逆向还原的方式进行图像生成的深度生成模型。其基本流程包括:
- 前向过程(Forward Process):将真实图像逐步加噪,最终变为高斯噪声。
- 反向过程(Reverse Process):学习一个模型从噪声中恢复图像。
这种方法具备以下优点:
- 稳定的训练过程;
- 高质量的图像生成效果;
- 可用于多模态、条件生成等任务。
该方法与之前的 VAE、GAN 等形成鲜明对比,它不直接建模图像分布,而是借助 Markov 链将采样任务转化为连续去噪。
Denoising Diffusion Probabilistic Models (DDPMs)
Overview of DDPM
Denoising Diffusion Probabilistic Models (DDPMs) 包括两个核心阶段:
- Forward Process:从真实图像逐步加入噪声,破坏其结构,最终变为高斯噪声。
- Reverse Process:学习一个去噪器(神经网络)从高斯噪声反向恢复图像结构。
Forward Process 定义
Forward 过程是一个马尔可夫过程:
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)
其中:
-
β t ∈ ( 0 , 1 ) \beta_t \in (0, 1) βt∈(0,1):是一个小的正数,用于控制每步噪声添加强度。
从t=0到t=T叫做noise schedule. 通常是一个小的数,确保数据被缩小,并且方差不会爆炸。
Ho et al.,建议 β 0 \beta_0 β0 = 0.0001 到 β 1000 \beta_{1000} β1000∈0.02.
-
1 − β t \sqrt{1 - \beta_t} 1−βt:控制当前步保留多少上一步的信息。
-
β t I \beta_t I βtI:控制当前步加入多少新噪声。
-
N是正态分布
-
x t x_t xt是输出
-
1 − β t x t − 1 \sqrt{1 - \beta_t}x_{t-1} 1−βtxt−1是均值
联合分布可写为:
q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) q(x_{1:T} | x_0) = \prod_{t=1}^T q(x_t | x_{t-1}) q(x1:T∣x0)=t=1∏Tq(xt∣xt−1)
Forward Process 中的 Noise Schedule
噪声调度(noise schedule)选择对模型表现影响巨大。Ho 等人建议的线性增长方式如下:
β t ∈ ( 0.0001 , 0.02 ) \beta_t \in (0.0001, 0.02) βt∈(0.0001,0.02)
为了进一步简化推导,我们定义:
α t = 1 − β t , α ˉ t = ∏ s = 1 t α s \alpha_t = 1 - \beta_t, \quad \bar{\alpha}_t = \prod_{s=1}^t \alpha_s αt=1−βt,αˉt=s=1∏tαs
这将帮助我们将任意时间步 x t x_t xt 直接表示为关于 x 0 x_0 x0 的函数,而不需要按顺序采样。
任意时间步的封闭采样公式(closed form)
通过:
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1- \beta_t}x_{t-1}, \beta_t I) q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)
我们有:
q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I) q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)
这被称为 Diffusion Kernel,意味着我们可以直接从 x 0 x_0 x0 中采样任意时刻的 x t x_t xt。
推导封闭形式采样的过程(Proof Sketch)
我们希望推导出一种简洁的表达形式,使得在已知初始数据 x 0 x_0 x0 的情况下,可以直接采样任意时刻 x t x_t xt,而不必逐步迭代。这是 Diffusion 模型高效训练和推理的关键。
定义
我们首先引入两个关键定义:
- α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt
- α ˉ t = ∏ s = 1 t α s \bar{\alpha}_t = \prod_{s=1}^t \alpha_s αˉt=∏s=1tαs
α ˉ t \bar{\alpha}_t αˉt 表示从时间 0 0 0 到 t t t 所有 α t \alpha_t αt 的乘积。
Forward Process 的定义
原始的前向扩散过程由下式给出:
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t ⋅ x t − 1 , β t I ) q(x_t \mid x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} \cdot x_{t-1}, \beta_t I) q(xt∣xt−1)=N(xt;1−βt⋅xt−1,βtI)
利用 α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt,改写为:
x t = α t x t − 1 + 1 − α t ϵ t − 1 , ϵ t − 1 ∼ N ( 0 , I ) x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-1}, \quad \epsilon_{t-1} \sim \mathcal{N}(0, I) xt=αtxt−1+1−αtϵt−1,ϵt−1∼N(0,I)
重参数化展开
我们希望将 x t x_t xt 表达为关于 x 0 x_0 x0 和高斯噪声的函数。
从上述公式出发,开始展开:
x t = α t x t − 1 + 1 − α t ϵ t − 1 x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-1} xt=αtxt−1+1−αtϵt−1
将 x t − 1 x_{t-1} xt−1 再展开为:
x t − 1 = α t − 1 x t − 2 + 1 − α t − 1 ϵ t − 2 x_{t-1} = \sqrt{\alpha_{t-1}} x_{t-2} + \sqrt{1 - \alpha_{t-1}} \epsilon_{t-2} xt−1=αt−1xt−2+1−αt−1ϵt−2
代入 x t x_t xt 中:
x t = α t α t − 1 x t − 2 + α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 x_t = \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t (1 - \alpha_{t-1})} \epsilon_{t-2} + \sqrt{1 - \alpha_t} \epsilon_{t-1} xt=αtαt−1xt−2+αt(1−αt−1)ϵt−2+1−αtϵt−1
继续递归展开,我们得到:
x t = α t α t − 1 ⋯ α 1 x 0 + 多项高斯噪声加权和 x_t = \sqrt{\alpha_t \alpha_{t-1} \cdots \alpha_1} x_0 + \text{多项高斯噪声加权和} xt=αtαt−1⋯α1x0+多项高斯噪声加权和
由于高斯变量的加权和仍然服从高斯分布,我们可以将所有噪声项合并成一个等效的高斯变量:
x t = α ˉ t x 0 + 1 − α ˉ t ⋅ ϵ , ϵ ∼ N ( 0 , I ) x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \cdot \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) xt=αˉtx0+1−αˉt⋅ϵ,ϵ∼N(0,I)
得到封闭形式的 Diffusion Kernel
于是我们就得到了一个封闭形式的采样公式:
q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q(x_t \mid x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I) q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)
这一公式说明我们无需一步一步从 x 0 x_0 x0 扩散到 x t x_t xt,而是可以直接采样任意时间步的 x t x_t xt,大大加快了训练过程。
噪声调度策略对比(Noise Schedule Improvements)
问题: Ho 等人的线性调度会快速降低 α ˉ t \bar{\alpha}_t αˉt,导致图像信息太快丢失。
改进方案: Dhariwal 和 Nichol 提出使用余弦函数作为调度:
α ˉ t = f ( t ) f ( 0 ) , f ( t ) = cos 2 ( t / T + s 1 + s ⋅ π 2 ) \bar{\alpha}_t = \frac{f(t)}{f(0)}, \quad f(t) = \cos^2\left( \frac{t/T + s}{1 + s} \cdot \frac{\pi}{2} \right) αˉt=f(0)f(t),f(t)=cos2(1+st/T+s⋅2π)
- Linear 调度: 蓝色曲线,下降较快。
- Cosine 调度: 橙色曲线,下降更慢,更平滑。

效果图(下图)显示:
- 上排(linear)图像更快被完全扰乱。
- 下排(cosine)保留更多结构,有助于训练稳定性。
在这里插入图片描述
Reverse Process 与其公式推导详解
本节展示了扩散模型中的逆过程(Reverse Process)如何从纯噪声逐步生成数据点,以及其数学表达和推导方式。
概述

逆过程图中描述了从高斯噪声 x T ∼ N ( 0 , I ) \mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) xT∼N(0,I) 开始的逐步采样过程:通过网络 p θ ( x t − 1 ∣ x t ) p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) pθ(xt−1∣xt) 不断采样,直到重构出 x 0 \mathbf{x}_0 x0。
在已知某一时刻的“噪声状态” x t \mathbf{x}_{t} xt 后,模型 p θ p_{\theta} pθ 预测一个前一时刻(更少噪声)的状态 x t − 1 \mathbf{x}_{t-1} xt−1 的条件概率分布。
这个分布是什么意思?
- 在正向过程中,原始数据 x 0 \mathbf{x}_0 x0 会逐步添加噪声得到 x 1 , x 2 , . . . , x T \mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_T x1,x2,...,xT。
- 而在逆向过程中,我们希望从纯噪声 x T ∼ N ( 0 , I ) \mathbf{x}_T \sim \mathcal{N}(0, I) xT∼N(0,I) 逐步去噪,一步步得到最终的数据样本 x 0 \mathbf{x}_0 x0。
- 这个“去噪”的每一步,就是由 p θ ( x t − 1 ∣ x t ) p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) pθ(xt−1∣xt) 来实现的。它告诉我们:在时刻 t t t 已知 x t \mathbf{x}_{t} xt,该如何采样更少噪声的 x t − 1 \mathbf{x}_{t-1} xt−1。
其中:
- 如果每一步的噪声添加 β t \beta_t βt 足够小,那么 q ( x t − 1 ∣ x t ) q(\mathbf{x}_{t-1}|\mathbf{x}_t) q(xt−1∣xt) 近似高斯分布。
- 模型 p θ p_\theta pθ 的目标是学习一个去噪函数,使其逼近真实后验 q ( x t − 1 ∣ x t ) q(\mathbf{x}_{t-1}|\mathbf{x}_t) q(xt−1∣xt)。
为了便于学习和推导,我们借助 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0),也即条件在原始图像 x 0 \mathbf{x}_0 x0 上。
我们有:
q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 ) , β ~ t I ) q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I}) q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)
其中:
-
μ ~ ( x t , x 0 ) = 1 α ˉ t ( x t − 1 − α t 1 − α ˉ t ϵ t ) \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0) = \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \right) μ~(xt,x0)=αˉt1(xt−1−αˉt1−αtϵt)
-
β ~ t = 1 − α ˉ t − 1 1 − α ˉ t β t \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t β~t=1−αˉt1−αˉt−1βt
推导过程详解
我们希望通过贝叶斯规则,从两个边缘分布 q ( x t ∣ x t − 1 ) q(\mathbf{x}_t|\mathbf{x}_{t-1}) q(xt∣xt−1) 和 q ( x t ∣ x 0 ) q(\mathbf{x}_t|\mathbf{x}_0) q(xt∣x0) 推出联合分布 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0) 的显式高斯形式。
根据贝叶斯定理,我们有:
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) ⋅ q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \frac{q(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{x}_0) \cdot q(\mathbf{x}_{t-1} | \mathbf{x}_0)}{q(\mathbf{x}_t | \mathbf{x}_0)} q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1,x0)⋅q(xt−1∣x0)
由于 x t − 1 → x t → x 0 \mathbf{x}_{t-1} \to \mathbf{x}_t \to \mathbf{x}_0 xt−1→xt→x0 构成马尔可夫链,
一句话:只跟上一个状态有关
在条件概率意义下,当前状态 x t \mathbf{x}_t xt 所携带的关于原始数据 x 0 \mathbf{x}_0 x0 的信息已经“包含在它自己身上了”,因此 下一步 x t − 1 \mathbf{x}_{t-1} xt−1 的分布仅依赖于 x t \mathbf{x}_t xt,而不再依赖更早的 x t + 1 , x t + 2 , … \mathbf{x}_{t+1}, \mathbf{x}_{t+2}, \dots xt+1,xt+2,… 等。
因此有:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t ∣ x t − 1 ) q(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{x}_0) = q(\mathbf{x}_t | \mathbf{x}_{t-1}) q(xt∣xt−1,x0)=q(xt∣xt−1)
从而有:
q ( x t − 1 ∣ x t , x 0 ) ∝ q ( x t ∣ x t − 1 ) ⋅ q ( x t − 1 ∣ x 0 ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) \propto q(\mathbf{x}_t | \mathbf{x}_{t-1}) \cdot q(\mathbf{x}_{t-1} | \mathbf{x}_0) q(xt−1∣xt,x0)∝q(xt∣xt−1)⋅q(xt−1∣x0)
- q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0):表示在给定 x t \mathbf{x}_t xt 和原始样本 x 0 \mathbf{x}_0 x0 的条件下,变量 x t − 1 \mathbf{x}_{t-1} xt−1 的后验分布,是我们希望建模的目标。
- q ( x t ∣ x t − 1 ) q(\mathbf{x}_t | \mathbf{x}_{t-1}) q(xt∣xt−1):表示扩散的前向过程,在已知 x t − 1 \mathbf{x}_{t-1} xt−1 的前提下,如何产生出 x t \mathbf{x}_t xt。这个分布是已知的(高斯分布)。
- q ( x t − 1 ∣ x 0 ) q(\mathbf{x}_{t-1} | \mathbf{x}_0) q(xt−1∣x0):表示从原始样本 x 0 \mathbf{x}_0 x0 直接扩散到 x t − 1 \mathbf{x}_{t-1} xt−1 的分布,也是高斯的,可以通过递推得到。
- ∝ \propto ∝:表示成比例关系,即我们省略了分母中的归一化项 q ( x t ∣ x 0 ) q(\mathbf{x}_t|\mathbf{x}_0) q(xt∣x0),这在后续使用时可以恢复为一个高斯分布。
我们假设这两个项都是高斯分布,分别写成:
- q ( x t ∣ x t − 1 ) = N ( α t x t − 1 , β t I ) q(\mathbf{x}_t|\mathbf{x}_{t-1}) = \mathcal{N}(\sqrt{\alpha_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}) q(xt∣xt−1)=N(αtxt−1,βtI)
- q ( x t − 1 ∣ x 0 ) = N ( α ˉ t − 1 x 0 , ( 1 − α ˉ t − 1 ) I ) q(\mathbf{x}_{t-1}|\mathbf{x}_0) = \mathcal{N}(\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0, (1 - \bar{\alpha}_{t-1}) \mathbf{I}) q(xt−1∣x0)=N(αˉt−1x0,(1−αˉt−1)I)
为了推导出联合概率的形式,我们用高斯概率密度函数的一般形式:
N ( x ; μ , σ 2 ) ∝ exp ( − 1 2 σ 2 ( x − μ ) 2 ) \mathcal{N}(\mathbf{x}; \mu, \sigma^2) \propto \exp\left( -\frac{1}{2\sigma^2} (\mathbf{x} - \mu)^2 \right) N(x;μ,σ2)∝exp(−2σ21(x−μ)2)
代入两个高斯项:
第一步:
展开联合分布密度:
q ( x t − 1 ∣ x t , x 0 ) ∝ exp ( − 1 2 β t ( x t − α t x t − 1 ) 2 ) ⋅ exp ( − 1 2 ( 1 − α ˉ t − 1 ) ( x t − 1 − α ˉ t − 1 x 0 ) 2 ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) \propto \exp\left( -\frac{1}{2 \beta_t} (\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2 \right) \cdot \exp\left( -\frac{1}{2 (1 - \bar{\alpha}_{t-1})} (\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2 \right) q(xt−1∣xt,x0)∝exp(−2βt1(xt−αtxt−1)2)⋅exp(−2(1−αˉt−1)1(xt−1−αˉt−1x0)2)
第二步:
把两个平方项都展开,得到:
- ( x t − α t x t − 1 ) 2 = x t 2 − 2 α t x t x t − 1 + α t x t − 1 2 (\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2 = \mathbf{x}_t^2 - 2 \sqrt{\alpha_t} \mathbf{x}_t \mathbf{x}_{t-1} + \alpha_t \mathbf{x}_{t-1}^2 (xt−αtxt−1)2=xt2−2αtxtxt−1+αtxt−12
- ( x t − 1 − α ˉ t − 1 x 0 ) 2 = x t − 1 2 − 2 α ˉ t − 1 x t − 1 x 0 + α ˉ t − 1 x 0 2 (\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2 = \mathbf{x}_{t-1}^2 - 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_{t-1} \mathbf{x}_0 + \bar{\alpha}_{t-1} \mathbf{x}_0^2 (xt−1−αˉt−1x0)2=xt−12−2αˉt−1xt−1x0+αˉt−1x02
将这两个带入指数中,并合并同类项(即 x t − 1 2 \mathbf{x}_{t-1}^2 xt−12, x t − 1 \mathbf{x}_{t-1} xt−1, 常数项等),可以合并成一个新的高斯形式:
exp ( − 1 2 β ~ t ( x t − 1 − μ ~ ( x t , x 0 ) ) 2 ) \exp\left( -\frac{1}{2 \tilde{\beta}_t} \left(\mathbf{x}_{t-1} - \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0)\right)^2 \right) exp(−2β~t1(xt−1−μ~(xt,x0))2)
从而得到:
q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 ) , β ~ t I ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I}) q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)
其中均值为:
μ ~ ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 β t 1 − α ˉ t x 0 \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0) = \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0 μ~(xt,x0)=1−αˉtαt(1−αˉt−1)xt+1−αˉtαˉt−1βtx0
方差为:
β ~ t = 1 − α ˉ t − 1 1 − α ˉ t ⋅ β t \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t β~t=1−αˉt1−αˉt−1⋅βt
这些表达式正是我们用于定义逆过程采样时的关键参数,它们说明给定 x t \mathbf{x}_t xt 和 x 0 \mathbf{x}_0 x0 后, x t − 1 \mathbf{x}_{t-1} xt−1 的条件分布是高斯的,均值和方差具有闭式形式。
我们有:
x t = α ˉ t x 0 + 1 − α ˉ t ϵ \mathbf{x}_t = \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon} xt=αˉtx0+1−αˉtϵ
变换得到:
x 0 = 1 α ˉ t ( x t − 1 − α ˉ t ϵ ) \mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon} \right) x0=αˉt1(xt−1−αˉtϵ)
将其代入 μ ~ ( x t , x 0 ) \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0) μ~(xt,x0):
μ ~ ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 β t 1 − α ˉ t x 0 = 1 α ˉ t ( x t − 1 − α t 1 − α ˉ t ϵ t ) \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0) = \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \right) μ~(xt,x0)=1−αˉtαt(1−αˉt−1)xt+1−αˉtαˉt−1βtx0=αˉt1(xt−1−αˉt1−αtϵt)
最后,我们得到条件高斯分布形式如下:
q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 ) , β ~ t I ) q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I}) q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)
这就是我们在逆过程(Reverse Process)中所使用的构造形式。
Learning Objective
我们可以像训练变分自编码器一样,通过最大化变分下界(Variational Lower Bound, ELBO)来优化扩散模型中的负对数似然目标:
− E q ( x 0 ) [ log p θ ( x 0 ) ] ≤ E q ( x 0 : T ) [ log p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] = : L -\mathbb{E}_{q(\mathbf{x}_0)}[\log p_\theta(\mathbf{x}_0)] \leq \mathbb{E}_{q(\mathbf{x}_{0:T})}\left[\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}\right] =: L −Eq(x0)[logpθ(x0)]≤Eq(x0:T)[logq(x1:T∣x0)pθ(x0:T)]=:L
根据 Sohl-Dickstein et al. (2015) 和 Ho et al. (2020),该目标可分解为:
L = E q [ D K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) ⏟ L T + ∑ t > 1 D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ⏟ L t − 1 − log p θ ( x 0 ∣ x 1 ) ⏟ L 0 ] L = \mathbb{E}_q \left[ \underbrace{D_{\mathrm{KL}}(q(\mathbf{x}_T|\mathbf{x}_0) \| p(\mathbf{x}_T))}_{L_T} + \sum_{t>1} \underbrace{D_{\mathrm{KL}}(q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) \| p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t))}_{L_{t-1}} - \underbrace{\log p_\theta(\mathbf{x}_0|\mathbf{x}_1)}_{L_0} \right] L=Eq LT DKL(q(xT∣x0)∥p(xT))+t>1∑Lt−1 DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))−L0 logpθ(x0∣x1)
由于 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0) 和 p θ ( x t − 1 ∣ x t ) p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t) pθ(xt−1∣xt) 都是高斯分布,因此 KL 散度有解析表达式。
对于 L t − 1 L_{t-1} Lt−1:
L t − 1 = D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) L_{t-1} = D_{\mathrm{KL}}(q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) \| p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)) Lt−1=DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))
代入两个分布的参数后有:
= E x 0 ∼ q ( x 0 ) , ϵ ∼ N ( 0 , I ) [ 1 2 ∥ Σ θ ( x t , t ) ∥ 2 ∥ μ ~ t ( x t , x 0 ) − μ θ ( x t , t ) ∥ 2 ] + C = \mathbb{E}_{\mathbf{x}_0 \sim q(\mathbf{x}_0), \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})} \left[ \frac{1}{2 \|\Sigma_\theta(\mathbf{x}_t, t)\|^2} \left\| \widetilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) - \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) \right\|^2 \right] + C =Ex0∼q(x0),ϵ∼N(0,I)[2∥Σθ(xt,t)∥21∥μ t(xt,x0)−μθ(xt,t)∥2]+C
其中,
- μ ~ t \widetilde{\boldsymbol{\mu}}_t μ t 为 q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) q(xt−1∣xt,x0) 的均值
- μ θ \boldsymbol{\mu}_\theta μθ 为网络预测的 p θ p_\theta pθ 的均值
学习目标简化
我们回顾图中给出的:
μ ~ t ( x t , x 0 ) = 1 α ˉ t ( x t − 1 − α t 1 − α ˉ t ϵ ) \widetilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) = \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon} \right) μ t(xt,x0)=αˉt1(xt−1−αˉt1−αtϵ)
μ θ ( x t , x 0 ) = 1 α ˉ t ( x t − 1 − α t 1 − α ˉ t ϵ θ ( x t , t ) ) \boldsymbol{\mu}_\theta(\mathbf{x}_t, \mathbf{x}_0) = \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \right) μθ(xt,x0)=αˉt1(xt−1−αˉt1−αtϵθ(xt,t))
于是 L t − 1 L_{t-1} Lt−1 变成:
L t − 1 = D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) L_{t-1} = D_{\mathrm{KL}}(q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) \| p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)) Lt−1=DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))
= E x 0 ∼ q ( x 0 ) , ϵ ∼ N ( 0 , I ) [ 1 2 ∥ Σ θ ( x t , t ) ∥ 2 ∥ μ ~ t ( x t , x 0 ) − μ θ ( x t , t ) ∥ 2 ] + C = \mathbb{E}_{\mathbf{x}_0 \sim q(\mathbf{x}_0), \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})} \left[ \frac{1}{2 \|\Sigma_\theta(\mathbf{x}_t, t)\|^2} \left\| \widetilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) - \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) \right\|^2 \right] + C =Ex0∼q(x0),ϵ∼N(0,I)[2∥Σθ(xt,t)∥21∥μ t(xt,x0)−μθ(xt,t)∥2]+C
代入上式:
= E x 0 , ϵ [ 1 2 ∥ Σ θ ( x t , t ) ∥ 2 ∥ 1 α ˉ t ( x t − 1 − α t 1 − α ˉ t ϵ ) − 1 α ˉ t ( x t − 1 − α t 1 − α ˉ t ϵ θ ( x t , t ) ) ∥ 2 ] + C = \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \left[ \frac{1}{2 \|\Sigma_\theta(\mathbf{x}_t, t)\|^2} \left\| \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon} \right)- \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \right) \right\|^2 \right] + C =Ex0,ϵ[2∥Σθ(xt,t)∥21 αˉt1(xt−1−αˉt1−αtϵ)−αˉt1(xt−1−αˉt1−αtϵθ(xt,t)) 2]+C
化简得到:
= E x 0 , ϵ [ ( 1 − α t ) 2 2 α t ( 1 − α ˉ t ) ∥ Σ θ ( x t , t ) ∥ 2 ∥ ϵ − ϵ θ ( x t , t ) ∥ 2 ] + C = \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \left[ \frac{(1 - \alpha_t)^2}{2\alpha_t(1 - \bar{\alpha}_t)\|\Sigma_\theta(\mathbf{x}_t, t)\|^2} \left\| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \right\|^2 \right] + C =Ex0,ϵ[2αt(1−αˉt)∥Σθ(xt,t)∥2(1−αt)2∥ϵ−ϵθ(xt,t)∥2]+C
进一步设定 Σ θ ( x t , t ) = σ t 2 I \Sigma_\theta(\mathbf{x}_t, t) = \sigma_t^2 \mathbf{I} Σθ(xt,t)=σt2I,其中 σ t 2 = β t \sigma_t^2 = \beta_t σt2=βt,并且忽略掉前面的部分,得到简化的损失:
L t simple = E t ∼ [ 1 , T ] , x 0 , ϵ [ ∥ ϵ − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ , t ) ∥ 2 ] + C L_t^{\text{simple}} = \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}} \left[ \left\| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon}, t\right) \right\|^2 \right] +C Ltsimple=Et∼[1,T],x0,ϵ[ ϵ−ϵθ(αˉtx0+1−αˉtϵ,t) 2]+C
算法
Algorithm 1 Training
- repeat
- x 0 ∼ q ( x 0 ) \mathbf{x}_0 \sim q(\mathbf{x}_0) x0∼q(x0)
- t ∼ Uniform ( { 1 , … , T } ) t \sim \text{Uniform}(\{1, \dots, T\}) t∼Uniform({1,…,T})
- ϵ ∼ N ( 0 , I ) \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I}) ϵ∼N(0,I)
- Take gradient descent step on
∇ θ ∥ ϵ − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ , t ) ∥ 2 \nabla_\theta \left\| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon}, t) \right\|^2 ∇θ ϵ−ϵθ(αˉtx0+1−αˉtϵ,t) 2 - until converged
Algorithm 2 Sampling
1. x T ∼ N ( 0 , I ) \mathbf{x}_T \sim \mathcal{N}(0, \mathbf{I}) xT∼N(0,I)
2. for t = T , … , 1 t = T, \dots, 1 t=T,…,1 do
3. z ∼ N ( 0 , I ) \mathbf{z} \sim \mathcal{N}(0, \mathbf{I}) z∼N(0,I) if t > 1 t > 1 t>1, else z = 0 \mathbf{z} = 0 z=0
4. x t − 1 = 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ θ ( x t , t ) ) + σ t z \mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \right) + \sigma_t \mathbf{z} xt−1=αt1(xt−1−αˉt1−αtϵθ(xt,t))+σtz
5. end for
6. return x 0 \mathbf{x}_0 x0
网络结构(Network Architectures)
扩散模型(Diffusion Models)通常采用 U-Net 架构来构建噪声预测网络 ϵ θ ( x t , t ) \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) ϵθ(xt,t),该架构中包含 ResNet 残差块和自注意力(self-attention)层。
时间信息的表示通常采用正弦位置编码(sinusoidal positional embeddings)或随机傅里叶特征(random Fourier features),这些时间表示会被输入到残差块中,方式可以是简单的空间加法(spatial addition),也可以是通过自适应分组归一化(adaptive group normalization)完成。
U-Net 结构如下图所示:
- 蓝色箭头:卷积(conv 3×3, ReLU)
- 灰色箭头:复制与拼接(copy and crop)
- 红色箭头:最大池化(max pool 2×2)
- 浅绿色箭头:上采样卷积(up-conv 2×2)
- 深绿色箭头:1×1 卷积(conv 1×1)
参考文献:
Ronneberger et al., “U-Net: Convolutional Networks for Biomedical Image Segmentation”, MICCAI 2015

生成模型比较(Comparing Generative Models)
这张图总结了三类主流的生成模型:GAN、VAE 和 Diffusion Models 的训练流程及核心机制。

GAN(生成对抗网络)
- 目标:通过对抗训练生成与真实数据相似的样本。
- 结构:
- 生成器 G ( z ) G(z) G(z):输入随机噪声 z z z,输出生成样本 x ′ \mathbf{x}' x′。
- 判别器 D ( x ) D(\mathbf{x}) D(x):判断输入样本是否真实(0/1标签)。
- 损失设计:生成器和判别器相互博弈,通过最小最大优化来提升生成质量。
- 关键点:训练不稳定、易模式崩溃,但图像质量高。
VAE(变分自编码器)
- 目标:最大化变分下界(Evidence Lower Bound, ELBO)。
- 结构:
- 编码器 q ϕ ( z ∣ x ) q_\phi(\mathbf{z}|\mathbf{x}) qϕ(z∣x):将数据编码为潜变量 z z z。
- 解码器 p θ ( x ∣ z ) p_\theta(\mathbf{x}|\mathbf{z}) pθ(x∣z):从潜变量还原出原始数据 x ′ \mathbf{x}' x′。
- 关键点:优化目标可导、稳定,但生成图像较模糊。
Diffusion Models(扩散模型)
- 目标:通过逐步加噪并反向去噪实现数据生成。
- 结构:
- 前向过程:从 x 0 \mathbf{x}_0 x0 开始逐步加入高斯噪声,得到一系列噪声状态 x 1 , x 2 , . . . , z \mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{z} x1,x2,...,z。
- 反向过程:学习一个去噪网络,从 z \mathbf{z} z 开始逐步还原出数据。
- 关键点:训练稳定、样本多样性高,但采样速度较慢。
这三种模型分别代表了当前生成模型研究的三个主要方向,各有优劣,实际应用中可根据需求选择。
生成式学习三难困境(The Generative Learning Trilemma)
这张图展示了生成模型面临的“三难困境”,即很难同时在以下三个方面都表现优异:

- 高质量样本(High Quality Samples)
- 快速采样(Fast Sampling)
- 模式覆盖 / 多样性(Mode Coverage / Diversity)
不同类型的生成模型在这三方面的表现各有偏重:
-
GANs(生成对抗网络)
- 优势:生成样本质量高,采样速度快(一次前向传播即可生成图像)。
- 劣势:模式崩溃(mode collapse),样本多样性不足。
-
Diffusion Models(扩散模型)
- 优势:高质量 和 多样性好(采样分布更接近真实分布)。
- 劣势:采样慢,因为需要多步反向去噪。
-
VAEs(变分自编码器)
- 优势:模式覆盖广,具有理论上的最大似然支持。
- 劣势:生成样本质量相对较低。
研究进展
- Dharaiwal 和 Nichol (2021):
- 发现扩散模型在样本质量和多样性方面优于 GAN,但推理(采样)时间远远长于 GAN。
- 提出加速扩散模型采样的研究是当前的活跃方向,已有大量进展。
该图引用了 ICLR 2022 的论文:
Xiao et al., “Tackling the Generative Learning Trilemma with Denoising Diffusion GANs”
这项工作尝试结合 GAN 与 Diffusion 的优势,来解决这三难困境。
相关文章:

【深度学习】 19. 生成模型:Diffusion Models
Diffusion Models Diffusion Models 简介 Diffusion 模型是一类通过逐步添加噪声并再逆向还原的方式进行图像生成的深度生成模型。其基本流程包括: 前向过程(Forward Process):将真实图像逐步加噪,最终变为高斯噪声…...

JMeter 直连数据库
1.直连数据库的使用场景 1.1 参数化,例如登录使用的账户名密码都可以从数据库中取得 1.2 断言,查看实际结果和数据库中的预期结果是否一致 1.3 清理垃圾数据,例如插入一个用户,它的ID不能相同,在测试插入功能后将数据删…...

易路 iBuilder:解构企业 AI 落地困境,重构智能体时代生产力范式
一、从大模型到智能体的产业跃迁 2024 年堪称中国人工智能产业的 "战略拐点" 之年。当 DeepSeek R1 模型以 "技术 价格" 双重普惠模式掀起行业震荡时,各企业纷纷意识到,大模型的真正价值不在于技术炫技,而在于成为企业…...

数据库,Spring Boot,数据源
您是对的,我之前的回答解释了Spring Boot在操作MySQL时不一定需要显式配置指定的数据源类型,因为它有自动配置机制,但没有直接点明在自动配置情况下“数据源是什么”。 在Spring Boot自动配置机制下,这个“数据源”指的是一个连接…...

Linux 第三阶段课程:数据库基础与 SQL 应用
数据库定义 数据库是按一定规则存储数据的仓库,可存储海量数据(百万级至亿级),数据来源包括文本、图像、音视频等多种形式,如出行记录、消费数据等。 数据库分类 关系型数据库:基于二维表格模型࿰…...

计算机网络之路由表更新
1.解题思路 对新接收到的路由表进行更新,全部"距离"1,且"下一跳路由器"都写成发送方路由器的名称。 开始对比新表和原来的路由表 1.看目的网络 如果是新的目的网络,则直接把对应的各项信息填入表中;如果是相同…...

万兴PDF手机版
万兴PDF手机版(万兴PDF编辑器)是一款国产PDF编辑工具.万兴PDF安卓版提供PDF文档编辑,AI撰写摘要,文档签名,设置密码保护等功能,万兴PDF专家APP以简约风格及文档编辑功能为核心,支持多设备终端同步保存.全免 万兴 PDF 编辑器是一款功能强大的 PDF 编辑软件,它支持多种…...
Qt -使用OpenCV得到SDF
博客主页:【夜泉_ly】 本文专栏:【暂无】 欢迎点赞👍收藏⭐关注❤️ 目录 cv::MatdistanceTransform获得SDF 本文的目标, 是简单学习并使用OpenCV的相关函数, 并获得QImage的SDF(Signed Distance Field 有向距离场) 至…...

Python 中Vector类的格式化实现,重点拆解其超球面坐标系的设计精髓
📌 高维向量的格式化革新 在Vector类第5版中,格式化系统迎来重要升级: 坐标系转型:从Vector2d的极坐标(p’后缀)升级为超球面坐标(h’后缀),支持n维空间维度突破&#…...
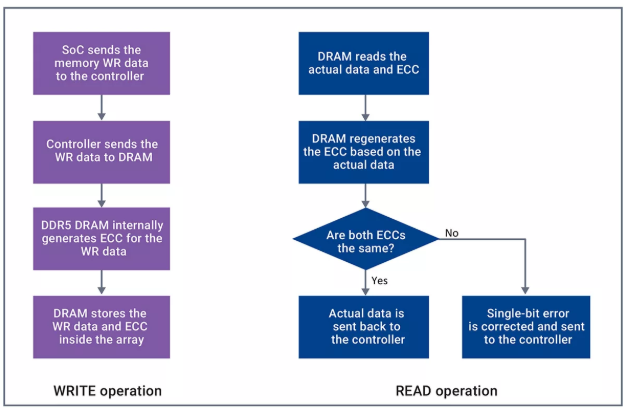
DDR5 ECC详细原理介绍与基于协议讲解
本文篇幅较长,涉及背景原理介绍方便大家理解其运作方式 以及 基于DDR5协议具体展开介绍。 背景原理介绍 上图参考:DDR 内存中的 ECC 写入操作时,On-die ECC的工作过程如下: SoC将需要写入到Memory中的数据发送给控制器控制器将需要写入的数据直接发送给DRAM芯片在DDR5 DR…...

Linux系统之gettext详解
gettext 是一个用于国际化(i18n)和本地化(l10n)的工具集,旨在帮助开发者创建多语言支持的应用程序。它主要通过提供一系列工具和库来简化文本翻译过程。 gettext 工作流程 标记源代码:在源代码中用 _() 函…...

基于Qt封装数据库基本增删改查操作,支持多线程,并实现SQLite数据库单例访问
抽出来的,直接用就行 头文件CPP文件使用示例 头文件 #ifndef DATABASECOMMON_H #define DATABASECOMMON_H/** 单例封装SQLite通用操作,支持多线程调用;可扩展兼容其他数据库,照着SysRunDatabase写,并且重载openDataba…...
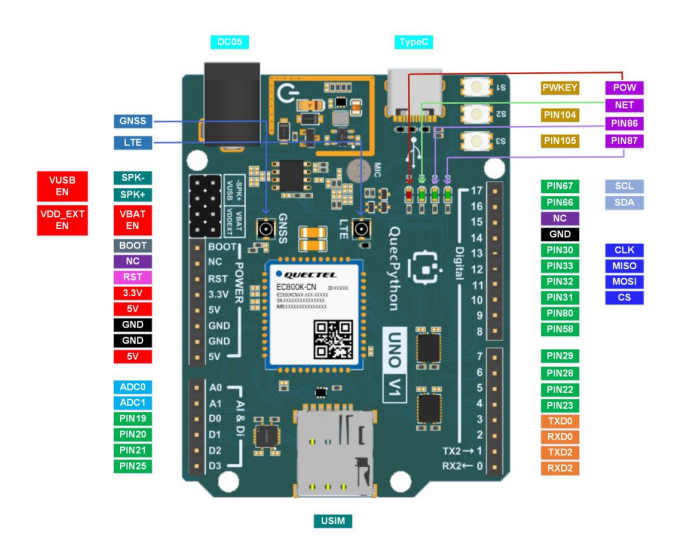
EC800X QuecDuino开发板介绍
支持的模组列表 EG800KEC800MEC800GEC800E 功能列表 基本概述 EC800X QuecDuino EVB 搭载移远 EC800 系列模组。支持模组型号为: EC800M 系列、EC800K 系列、EG800K 系列、EC800E 系列等。 渲染图 开发板的主要组件、接口布局见下图 资料下载 EC800X-QuecDui…...

ARM P15协处理器指令详解:架构、编程与应用实践
ARM P15协处理器指令详解:架构、编程与应用实践 引言 在ARM处理器架构中,协处理器(Coprocessor)系统是扩展处理器功能的关键机制,其中CP15(即协处理器15)作为系统控制协处理器,承担着内存管理、缓存控制、系统配置等核心功能。本…...

PHP轻量级聊天室源码(源码下载)
最新版本:v2.1.2 (2024.08更新) 运行环境:PHP5.6(无需MySQL) 核心特性:手机电脑自适应、TXT数据存储、50条历史消息 适用场景:小型社区/企业内网/教育培训即时通讯 一、核心功能亮点(SEO关键词布…...
)
MySQL数据表添加字段(三种方式)
基本概念解析 数据表由行和列组成,专业术语中: 字段(Field):表的纵向列结构记录(Record):表的横向行数据 字段添加方法详解 MySQL支持三种字段添加位置,语法格式均通…...

leetcode hot100刷题日记——33.二叉树的层序遍历
解题总结二维vector的初始化方法 题目描述情况1:不确定行数和列数情况2:已知行数和列数情况3:已知行数但不知道列数情况4:已知列数但不知道行数 题目描述 解答:用队列 思路都差不多,我觉得对于我自己来说&a…...

2、PyTorch基础教程:从张量到神经网络训练
1、PyTorch基础 PyTorch 是一个开源的深度学习框架,以其灵活性和动态计算图而广受欢迎。 PyTorch 主要有以下几个基础概念:张量(Tensor)、自动求导(Autograd)、神经网络模块(nn.Module…...

《数据结构初阶》【番外篇:快速排序的前世今生】
【番外篇:快速排序的前世今生】目录 前言:---------------起源---------------一、诞生:二、突破:三、核心: ---------------发展---------------1. 早期版本:简单但不稳定1960 年:初始版本 2. …...

【笔记】基于 MSYS2(MINGW64)的 Poetry 虚拟环境创建指南
#工作记录 基于 MSYS2(MINGW64)的 Poetry 虚拟环境创建指南 一、背景说明 在基于 MSYS2(MINGW64)的环境中,使用 Poetry 创建虚拟环境是一种高效且灵活的方式来管理 Python 项目依赖。本指南将详细介绍如何在 PyChar…...

PINNs案例——二维磁场计算
基于物理信息的神经网络是一种解决偏微分方程计算问题的全新方法… 有关PINN基础详见:PINNs案例——中心热源温度场预测问题的torch代码 今日分享代码案例:二维带电流源磁场计算 该案例参考学习论文:[1]张宇娇,孙宏达࿰…...

Hive SQL 中 BY 系列关键字全解析:从排序、分发到分组的核心用法
一、排序与分发相关 BY 关键字 1. ORDER BY:全局统一排序 作用:对查询结果进行全局排序,确保最终结果集完全有序(仅允许单个 Reducer 处理数据)。 语法: SELECT * FROM table_name ORDER BY column1 [A…...

数据类型检测有哪些方式?
typeof 其中数组 对象 null都会判断为Object,其他正确 typeof 2 // number typeof true //bolean typeof str //string typeof [] //Object typeof function (){} // function typeof {} //object typeof undefined //undefined typeof null // nullinstanceof 判断…...
算法打开13天
41.前 K 个高频元素 (力扣347题) 给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。 示例 1: 输入: nums [1,1,1,2,2,3], k 2 输出: [1,2]示例 2: 输入: nums [1], k 1 输出: …...

Freeqwq 世界首个免费无限制 分布式 AI 算力平台 https://qwq.aigpu.cn/
官网:Free QWQ - 免费分布式 AI 算力平台 基于来自全国各地 50 台家用电脑的 3090、4080、4090 显卡分布式算力,我们为开发者提供完全免费、无限制的 QwQ 32B 大语言模型 API。无需注册,无需充值,立即获取 API Key 开始使用。 …...

广告拦截器:全方位拦截,畅享无广告体验
在数字时代,广告无处不在。无论是浏览网页、使用社交媒体,还是观看视频,广告的频繁弹出常常打断我们的体验,让人不胜其烦。更令人担忧的是,一些广告可能包含恶意软件,威胁我们的设备安全和个人隐私。AdGuar…...

.net Avalonia应用程序生命周期
.NET Avalonia 应用程序生命周期全解析 在 .NET 开发领域,Avalonia 作为一个跨平台的 UI 框架,为开发者提供了强大的功能和灵活性。了解 Avalonia 应用程序的生命周期,对于构建高效、稳定的应用至关重要。本文将深入探讨 Avalonia 应用程序生…...

主数据编码体系全景解析:从基础到高级的编码策略全指南
在数字化转型的浪潮中,主数据管理(MDM)已成为企业数字化转型的基石。而主数据编码作为MDM的核心环节,其设计质量直接关系到数据管理的效率、系统的可扩展性以及业务决策的准确性。本文将系统性地探讨主数据编码的七大核心策略&…...

Selenium操作指南(全)
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 大家好,今天带大家一起系统的学习下模拟浏览器运行库Selenium,它是一个用于Web自动化测试及爬虫应用的重要工具。 Selenium测试直接运行在…...

Go语言中的数据类型转换
Go 语言中只有强制类型转换,没有隐式类型转换。 1. 数值类型之间的相互转换 1.1. 整型和整型之间的转换 package main import "fmt"func main() {var a int8 20var b int16 40fmt.Println(int16(a) b)// 60 }1.2. 浮点型和浮点型之间的转换 packag…...
