LeetCode算法题 （搜索二维矩阵）Day18！！！C/C++

https://leetcode.cn/problems/search-a-2d-matrix/description/

一、题目分析

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

二、示例分析

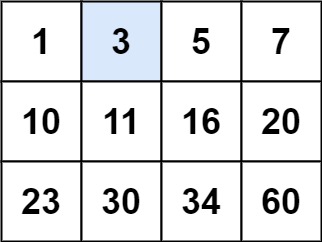
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

从题目及示例可知，我们的任务是在一个二维数组中查找目标值。若目标值存在于该二维数组中，返回true；否则，返回false。

今天的题目是一道经典的二分查找模板题。之前我们已经分享过二分算法相关内容，初次接触或有所遗忘的同学，可以点击链接回顾一下哦！https://blog.csdn.net/m0_75144071/article/details/145009380?spm=1001.2014.3001.5501

三、解题思路&代码实现

        方法一：暴力法     

        在之前的题目分享中，我们多次强调了暴力法的重要性。这种方法的核心思想是：题目要求什么，我们就直接实现什么，暂时不考虑优化。对于初学者来说，先确保能够完成题目要求是最重要的！

        所以暴力法我们也不难想出，题目要求在二维数组中搜索一个目标值，那么我们就直接枚举这个二维数组，如果枚举到目标值直接return true即可。下面看一下具体代码！

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {// 遍历二维数组的每一行for (int i = 0; i < matrix.size(); i++) {// 遍历当前行的每一个元素for (int j = 0; j < matrix[i].size(); j++) {// 如果找到目标值，立即返回trueif (matrix[i][j] == target)return true;}}// 遍历完整个数组后仍未找到目标值，返回falsereturn false;}
};

         方法二：二分算法（逐行二分）

        方法一虽然简单，在LeetCode上也能顺利通过，但这是因为本题的数据量较小。即便n和m都取最大值100，数据范围也只有10^4。如果遇到数据范围较大的情况，方法一可能就难以通过所有测试用例了。

        这时，更高效的算法就该登场了！二分查找算法的时间复杂度仅为O(logn)，相比方法一的O(mn)有了显著提升，运行速度将大大提高。下面来看一下具体的实现代码！（下方代码的时间复杂度为O(Mlogn)，这里请大家自行分析一下！)

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {// 遍历二维数组的每一行for (int i = 0; i < matrix.size(); i++) {// 初始化二分查找的左右边界：左边界为0，右边界为当前行的最后一个元素索引int left = 0, right = matrix[i].size() - 1;// 二分查找循环：当左边界不超过右边界时继续搜索while (left <= right) {// 计算中间位置：使用位运算 >> 1 代替除以2，效率更高int mid = left + right >> 1;// 中间元素小于目标值，说明目标在右半部分，更新左边界if (matrix[i][mid] < target)left = mid + 1;// 中间元素大于目标值，说明目标在左半部分，更新右边界else if (matrix[i][mid] > target)right = mid - 1;// 找到目标值，立即返回trueelsereturn true;        }}// 所有行搜索完毕后仍未找到目标值，返回falsereturn false;}
};

具体的思路就是，我们把二维数组想象成有m个大小为n的一维数组，每次去大小为n的二维数组中搜索目标值。而二分算法中最关键的一点，就是需要有序，题目中给出了每行内部有序，所以我们不用在对数组进行排序。

        方法三：二分算法（库函数优化）

        方法二的时间复杂度已是最优，不过我们可以进一步简化代码实现。

        这里就要用到我们C++自带的库函数了，C++中内涵两个二分的库函数，分别是upper_bound和lower_bound。下面来带大家简单了解一下这两个函数的功能。

函数	返回值规则	等价元素处理	[10,20,20,30]
lower_bound(val)	返回 第一个≥val 的元素位置	指向第一个等于 val 的元素	lower_bound(20) → 指向第一个 20 （索引1）
upper_bound(val)	返回 第一个>val 的元素位置	指向最后一个等于 val 的 下一个位置	upper_bound(20) → 指向 30 （索引3）

// 在 [first, last) 范围内查找
iterator lower_bound(iterator first, iterator last, const T& val);
iterator upper_bound(iterator first, iterator last, const T& val);

        其中first和last两个参数为迭代器，表示搜索的范围（左闭右开区间）val表目标值。

如果找到则返回第一个满足的条件的元素的迭代器，若未找到，则返回last。

   

在这道题中，我们应该选择 lower_bound 而非 upper_bound，因为 lower_bound 能够精准定位到第一个大于或等于目标值的元素，而这正是我们需要的。具体分析如下：

1. 目标明确：题目要求判断二维数组中是否存在目标值 target，我们需要找到第一个等于 target 的位置。
2. lower_bound 的优势：它返回的迭代器指向第一个大于或等于 target 的元素。如果该元素恰好等于 target，则说明存在；否则（元素大于 target 或超出数组范围），说明不存在。
3. upper_bound 的局限性：它返回的是第一个大于 target 的元素，无法直接判断 target 是否存在。即使存在，返回的位置也会跳过目标值，需要额外向前查找，增加复杂度。

下面来看一下具体的代码实现！

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {// 遍历二维数组的每一行for (auto& row : matrix) {// 对当前行使用 lower_bound 进行二分查找// lower_bound 返回第一个 >=target 的元素迭代器auto it = lower_bound(row.begin(), row.end(), target);// 检查迭代器是否有效（未越界）且找到的元素等于 targetif (it != row.end() && *it == target)return true;  // 找到目标值，返回 true}return false;  // 所有行遍历完毕，未找到目标值}
};

使用 C++ 的 lower_bound 库函数确实能让代码的简洁性和可读性得到显著提升，同时还能减少手动实现二分查找时容易出现的边界条件错误。不过，我强烈建议大家在熟练掌握二分查找的底层逻辑，能够在任何二分题目中手写出正确的二分算法之后，再去使用这两个库函数。

        方法四：二分算法（压缩映射）

        以上的二分算法的时间复杂度都为O(M logn)，其实还可以在对这段代码进行进一步的优化，也就是压缩映射。

        压缩映射利用了空间的连续性二维数组在内存中通常按行优先存储（如 C++），即同一行的元素连续存储。通过公式 k = i×n + j，可将二维位置无损压缩为一维索引，保持内存连续性。

        而题目也给出了行内部有序与行与行之间有序。所以映射以后的数组也是保持有序的。

核心映射公式

对于一个 m 行 n 列的二维数组 matrix，其元素 matrix[i][j] 可映射为一维数组的索引 k：

k=i×n+j

其中：

 

• i 是行索引（范围：0 ≤ i < m）
• j 是列索引（范围：0 ≤ j < n）
• k 是一维索引（范围：0 ≤ k < m×n）

 

逆映射公式：从一维索引 k 恢复二维坐标：

i=⌊k/n⌋,j=k%n

 关于公式推导，留给同学们作为练习。接下来我们直接进入算法优化部分。

​
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size();int n = matrix[0].size();// 将二维矩阵视为一维有序数组进行二分查找// 初始化左右边界：左边界为0，右边界为矩阵元素总数减1int left = 0, right = m * n - 1;// 标准二分查找循环条件while (left <= right) {// 计算中间索引，避免(left+right)可能的整数溢出int mid = left + (right - left) / 2;// 将一维索引转换为二维矩阵中的行列坐标// mid / n 计算行号，mid % n 计算列号int val = matrix[mid / n][mid % n];// 找到目标值，立即返回if (val == target)return true;// 当前值小于目标值，调整左边界到mid+1else if (val < target)left = mid + 1;// 当前值大于目标值，调整右边界到mid-1elseright = mid - 1;}// 二分查找结束后仍未找到目标值return false;}
};​

四、题目总结

一、核心考点

本题为经典的有序矩阵二分查找问题，主要考察以下能力：

1. 有序性利用：通过矩阵的 “每行内部有序” 和 “行间递增” 特性，将二维搜索转化为一维问题。
2. 二分查找算法：包括手动实现二分逻辑、使用标准库函数（如 lower_bound）、以及通过数学映射（压缩映射）优化效率。

二、关键思路与解法对比

解法	时间复杂度	空间复杂度	核心逻辑
暴力法	O(mn)	O(1)	逐行逐元素遍历，适用于小规模数据。
逐行二分	O(mlogn)	O(1)	对每行独立二分查找，利用每行有序性。
库函数优化	O(mlogn)	O(1)	使用 lower_bound 简化代码，避免手动处理边界。
压缩映射	O(log(mn))	O(1)	将二维矩阵映射为一维有序数组，全局二分查找，效率最优。

三、核心知识点

1. 二分查找模板：

   • 循环条件：left <= right（闭区间）或 left < right（开区间）。
   • 中点计算：mid = left + (right - left) / 2（避免整数溢出）。
   • 边界调整：根据中点值与目标值的大小关系收缩搜索区间。

2. 压缩映射原理：

   • 二维坐标转一维索引：k = i \times n + j（n 为列数）。
   • 一维索引转二维坐标：i = k // n, j = k % n。
   • 适用条件：矩阵需全局有序（每行首元素 > 前一行尾元素）。

3. C++ 标准库函数：

   • lower_bound：返回第一个**≥目标值**的元素位置，用于判断存在性。
   • upper_bound：返回第一个 **> 目标值 ** 的元素位置，用于范围查询。

四、易错点与优化建议

1. 边界条件：

   • 空矩阵处理：需先判断 matrix.size() == 0 或 matrix[0].size() == 0。
   • 索引越界：确保一维索引 k 在 [0, m*n-1] 范围内。

2. 效率优化：

   • 若矩阵全局有序，优先使用压缩映射的全局二分（O(log(mn))）。
   • 避免重复造轮子：熟练掌握二分逻辑后，合理使用 lower_bound 提升代码简洁性。

五、总结

        本题通过不同层次的解法展示了算法优化的思路：从暴力枚举到利用有序性的二分查找，再到通过数学映射实现全局最优解。核心在于深入理解题目条件（有序性），并选择合适的数据结构与算法降低时间复杂度。熟练掌握二分查找的原理和变种，是解决此类问题的关键。谢谢大家的收看！荆轲刺秦！！！