由浅入深一文详解同余原理
由浅入深一文详解同余原理
- 一、同余原理的基本概念
- 1.1 同余的定义
- 1.2 剩余类与完全剩余系
- 二、同余原理的基本性质
- 2.1 自反性
- 2.2 对称性
- 2.3 传递性
- 2.4 加减性
- 2.5 乘性
- 2.6 幂性
- 三、同余原理的运算与应用
- 3.1 同余运算在计算中的应用
- 3.2 密码学中的应用
- 3.3 日期与周期问题
- 四、案例分析:快速幂取模
- 问题描述
- 核心原理
- 代码实现:快速幂取模算法
- Python实现
- C++实现
- Java实现
- 代码解析
- 同余原理案例中的应用
- 应用扩展:RSA加密中的模幂运算
同余原理是数论中一个基础且重要的概念,它为我们研究整数之间的关系提供了独特的视角和强大的工具,在数学、计算机科学、密码学、信息安全等实际应用中发挥着关键作用。本文我将深入探讨同余原理的基本概念、性质、运算规则以及实际应用,带你全面理解这一重要原理,废话不多说直接发车。
一、同余原理的基本概念
1.1 同余的定义
给定一个正整数 m m m,如果两个整数 a a a 和 b b b 满足 a − b a - b a−b 能够被 m m m 整除,即 ( a − b ) ÷ m (a - b) \div m (a−b)÷m 的结果是整数,那么就称整数 a a a 与 b b b 对模 m m m 同余,记作 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm)。其中, m m m 称为模, ≡ \equiv ≡ 是同余符号 。例如,因为 17 − 5 = 12 17 - 5 = 12 17−5=12, 12 12 12 能被 6 6 6 整除,所以可以表示为 17 ≡ 5 ( m o d 6 ) 17 \equiv 5 \pmod{6} 17≡5(mod6);再如 25 − 10 = 15 25 - 10 = 15 25−10=15, 15 15 15 能被 5 5 5 整除,即 25 ≡ 10 ( m o d 5 ) 25 \equiv 10 \pmod{5} 25≡10(mod5)。
从直观上理解,同余表示两个整数在除以同一个模 m m m 时,具有相同的余数。例如, 17 ÷ 6 = 2 ⋯ ⋯ 5 17 \div 6 = 2\cdots\cdots5 17÷6=2⋯⋯5, 5 ÷ 6 = 0 ⋯ ⋯ 5 5 \div 6 = 0\cdots\cdots5 5÷6=0⋯⋯5,它们除以 6 6 6 的余数都是 5 5 5,这也是同余的另一种等价理解方式。
1.2 剩余类与完全剩余系
-
剩余类:对于给定的模 m m m,所有与整数 a a a 同余的整数构成的集合,称为 a a a 关于模 m m m 的剩余类,记作 [ a ] m [a]_m [a]m。例如,对于模 3 3 3, [ 0 ] 3 = { ⋯ , − 3 , 0 , 3 , 6 , ⋯ } [0]_3 = \{ \cdots, -3, 0, 3, 6, \cdots \} [0]3={⋯,−3,0,3,6,⋯}, [ 1 ] 3 = { ⋯ , − 2 , 1 , 4 , 7 , ⋯ } [1]_3 = \{ \cdots, -2, 1, 4, 7, \cdots \} [1]3={⋯,−2,1,4,7,⋯}, [ 2 ] 3 = { ⋯ , − 1 , 2 , 5 , 8 , ⋯ } [2]_3 = \{ \cdots, -1, 2, 5, 8, \cdots \} [2]3={⋯,−1,2,5,8,⋯}。每个剩余类中的任意两个整数都对模 m m m 同余,并且整数集可以被划分为 m m m 个互不相交的剩余类。
-
完全剩余系:从模 m m m 的每个剩余类中各取一个整数,得到的由 m m m 个整数组成的集合,称为模 m m m 的一个完全剩余系。例如,对于模 4 4 4, { 0 , 1 , 2 , 3 } \{0, 1, 2, 3\} {0,1,2,3} 是一个完全剩余系, { 4 , 5 , 6 , 7 } \{4, 5, 6, 7\} {4,5,6,7} 同样也是模 4 4 4 的一个完全剩余系 。
二、同余原理的基本性质
2.1 自反性
对于任意整数 a a a 和正整数 m m m,都有 a ≡ a ( m o d m ) a \equiv a \pmod{m} a≡a(modm)。这是因为 a − a = 0 a - a = 0 a−a=0, 0 0 0 能被任何正整数 m m m 整除,所以一个整数自身必然与自身对模 m m m 同余。
2.2 对称性
若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm),则 b ≡ a ( m o d m ) b \equiv a \pmod{m} b≡a(modm)。因为 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm) 意味着 a − b a - b a−b 能被 m m m 整除,那么 b − a = − ( a − b ) b - a = -(a - b) b−a=−(a−b) 也能被 m m m 整除,所以 b b b 与 a a a 对模 m m m 同余。
2.3 传递性
若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm) 且 b ≡ c ( m o d m ) b \equiv c \pmod{m} b≡c(modm),则 a ≡ c ( m o d m ) a \equiv c \pmod{m} a≡c(modm)。由 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm) 可得 a − b = k m a - b = km a−b=km( k k k 为整数),由 b ≡ c ( m o d m ) b \equiv c \pmod{m} b≡c(modm) 可得 b − c = l m b - c = lm b−c=lm( l l l 为整数),那么 a − c = ( a − b ) + ( b − c ) = ( k + l ) m a - c = (a - b) + (b - c) = (k + l)m a−c=(a−b)+(b−c)=(k+l)m,即 a − c a - c a−c 能被 m m m 整除,所以 a a a 与 c c c 对模 m m m 同余。
2.4 加减性
若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm), c ≡ d ( m o d m ) c \equiv d \pmod{m} c≡d(modm),则 a + c ≡ b + d ( m o d m ) a + c \equiv b + d \pmod{m} a+c≡b+d(modm), a − c ≡ b − d ( m o d m ) a - c \equiv b - d \pmod{m} a−c≡b−d(modm)。因为 a − b = k m a - b = km a−b=km, c − d = l m c - d = lm c−d=lm,所以 ( a + c ) − ( b + d ) = ( a − b ) + ( c − d ) = ( k + l ) m (a + c) - (b + d) = (a - b) + (c - d) = (k + l)m (a+c)−(b+d)=(a−b)+(c−d)=(k+l)m, ( a − c ) − ( b − d ) = ( a − b ) − ( c − d ) = ( k − l ) m (a - c) - (b - d) = (a - b) - (c - d) = (k - l)m (a−c)−(b−d)=(a−b)−(c−d)=(k−l)m,都能被 m m m 整除。
2.5 乘性
若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm), c ≡ d ( m o d m ) c \equiv d \pmod{m} c≡d(modm),则 a c ≡ b d ( m o d m ) ac \equiv bd \pmod{m} ac≡bd(modm)。将 a = b + k m a = b + km a=b+km, c = d + l m c = d + lm c=d+lm 代入 a c − b d ac - bd ac−bd 可得: a c − b d = ( b + k m ) ( d + l m ) − b d = b d m + b l m 2 + k d m + k l m 2 ac - bd = (b + km)(d + lm) - bd = bdm + blm^2 + kdm + klm^2 ac−bd=(b+km)(d+lm)−bd=bdm+blm2+kdm+klm2,显然 a c − b d ac - bd ac−bd 能被 m m m 整除。
2.6 幂性
若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm),那么对于任意正整数 n n n,有 a n ≡ b n ( m o d m ) a^n \equiv b^n \pmod{m} an≡bn(modm)。可以通过乘性进行递推证明,当 n = 1 n = 1 n=1 时显然成立,假设 a k ≡ b k ( m o d m ) a^k \equiv b^k \pmod{m} ak≡bk(modm),由乘性可得 a k + 1 = a k ⋅ a ≡ b k ⋅ b = b k + 1 ( m o d m ) a^{k + 1} = a^k \cdot a \equiv b^k \cdot b = b^{k + 1} \pmod{m} ak+1=ak⋅a≡bk⋅b=bk+1(modm) 。
三、同余原理的运算与应用
3.1 同余运算在计算中的应用
同余运算可以简化复杂的数值计算。例如,计算 2345 × 6789 m o d 11 2345 \times 6789 \bmod 11 2345×6789mod11,如果直接计算 2345 × 6789 2345 \times 6789 2345×6789 再取模,计算量较大。利用同余的乘性,先分别计算 2345 m o d 11 = 1 2345 \bmod 11 = 1 2345mod11=1, 6789 m o d 11 = 5 6789 \bmod 11 = 5 6789mod11=5,然后计算 1 × 5 m o d 11 = 5 1 \times 5 \bmod 11 = 5 1×5mod11=5,这样就大大简化了计算过程。
3.2 密码学中的应用
同余原理在密码学中有着广泛的应用,例如在 RSA 加密算法中,同余运算起到了核心作用。RSA 算法基于大整数分解的困难性,通过同余运算实现加密和解密过程。在加密时,利用同余的幂性对明文进行运算得到密文;解密时,同样依据同余原理进行反向运算恢复明文 。
3.3 日期与周期问题
在处理日期和周期相关的问题时,同余原理也非常有用。例如,已知今天是星期一,求 100 100 100 天后是星期几。一周有 7 7 7 天,以 7 7 7 为模, 100 m o d 7 = 2 100 \bmod 7 = 2 100mod7=2,因为今天是星期一,经过 100 100 100 天相当于在星期一的基础上再过 2 2 2 天,所以 100 100 100 天后是星期三。
四、案例分析:快速幂取模
问题描述
计算 a b m o d m a^b \mod m abmodm 的值,其中 a a a、 b b b 是非常大的整数(例如 b b b 是 10 5 10^5 105 级别的指数),直接计算 a b a^b ab 会导致数值溢出或计算效率低下。利用同余原理的幂性和模运算性质,可以高效地求解该问题。
核心原理
根据同余的幂性:若 a ≡ c ( m o d m ) a \equiv c \pmod{m} a≡c(modm),则 a b ≡ c b ( m o d m ) a^b \equiv c^b \pmod{m} ab≡cb(modm)。
结合快速幂算法(二分法),将指数 b b b 分解为二进制位,通过不断平方并取模,避免大数运算。
代码实现:快速幂取模算法
以下代码均实现 f ( a , b , m ) = a b m o d m f(a, b, m) = a^b \mod m f(a,b,m)=abmodm,适用于大数场景。
Python实现
def fast_pow_mod(a, b, m):result = 1a = a % m # 先对底数取模,避免初始值过大while b > 0:if b % 2 == 1:result = (result * a) % m # 奇数指数时乘入结果a = (a * a) % m # 底数平方并取模b = b // 2 # 指数减半return result# 示例:计算 3^100 mod 7
a = 3
b = 100
m = 7
print(f"{a}^{b} mod {m} = {fast_pow_mod(a, b, m)}") # 输出: 3^100 mod 7 = 4
C++实现
#include <iostream>
using namespace std;long long fast_pow_mod(long long a, long long b, long long m) {long long result = 1;a = a % m; // 底数取模while (b > 0) {if (b % 2 == 1) {result = (result * a) % m; // 奇数指数时乘入结果}a = (a * a) % m; // 底数平方取模b = b / 2; // 指数减半}return result;
}int main() {long long a = 3, b = 100, m = 7;cout << a << "^" << b << " mod " << m << " = " << fast_pow_mod(a, b, m) << endl; // 输出: 3^100 mod 7 = 4return 0;
}
Java实现
public class FastPowMod {public static long fastPowMod(long a, long b, long m) {long result = 1;a = a % m; // 底数取模while (b > 0) {if (b % 2 == 1) {result = (result * a) % m; // 奇数指数时乘入结果}a = (a * a) % m; // 底数平方取模b = b / 2; // 指数减半}return result;}public static void main(String[] args) {long a = 3, b = 100, m = 7;System.out.println(a + "^" + b + " mod " + m + " = " + fastPowMod(a, b, m)); // 输出: 3^100 mod 7 = 4}
}
代码解析
- 初始取模:对底数 a a a 先取模 m m m,确保初始值在合理范围内(利用同余原理 a ≡ a m o d m ( m o d m ) a \equiv a \mod m \pmod{m} a≡amodm(modm))。
- 快速幂逻辑:
- 当指数 b b b 为奇数时,将当前底数 a a a 乘入结果,并对结果取模。
- 每次将底数 a a a 平方并取模(利用同余的幂性: a 2 ≡ ( a m o d m ) 2 ( m o d m ) a^2 \equiv (a \mod m)^2 \pmod{m} a2≡(amodm)2(modm))。
- 指数 b b b 不断减半,直到变为 0,时间复杂度为 O ( log b ) O(\log b) O(logb)。
- 避免溢出:每次乘法后立即取模,防止中间结果超过数据类型范围。
同余原理案例中的应用
- 幂性应用:通过 a ≡ a m o d m ( m o d m ) a \equiv a \mod m \pmod{m} a≡amodm(modm),将大数 a a a 转换为等效的小数,简化计算。
- 模运算封闭性:加法、乘法在模运算下保持同余关系,即 ( a × b ) m o d m = [ ( a m o d m ) × ( b m o d m ) ] m o d m (a \times b) \mod m = [(a \mod m) \times (b \mod m)] \mod m (a×b)modm=[(amodm)×(bmodm)]modm,确保每一步计算结果等价于原始大数运算的结果。
应用扩展:RSA加密中的模幂运算
在RSA加密算法中,加密和解密过程本质上是大数的模幂运算(如 C = M e m o d n C = M^e \mod n C=Memodn, M = C d m o d n M = C^d \mod n M=Cdmodn)。上述快速幂取模算法是RSA的核心实现基础,利用同余原理确保加密和解密的正确性,同时通过高效计算应对大数场景。通过同余原理和快速算法,即使 e e e 和 d d d 是数百位的大整数,也能在合理时间内完成计算。
That’s all, thanks for reading!
觉得有用就点个赞、收进收藏夹吧!关注我,获取更多干货~
相关文章:

由浅入深一文详解同余原理
由浅入深一文详解同余原理 一、同余原理的基本概念1.1 同余的定义1.2 剩余类与完全剩余系 二、同余原理的基本性质2.1 自反性2.2 对称性2.3 传递性2.4 加减性2.5 乘性2.6 幂性 三、同余原理的运算与应用3.1 同余运算在计算中的应用3.2 密码学中的应用3.3 日期与周期问题 四、案…...

ESP-IDF 离线安装——同时存在多个版本以及进行版本切换的方法
一、离线安装包的下载方法 ESP-IDF离线安装包下载链接 我下载了下面三个版本进行测试 二、离线安装包的安装方法 1.创建文件夹 创建ESP-IDF文件夹,并为不同版本的IDF分别创建一个文件夹,如下图所示 2.双击离线安装包(以5.0版本为例&am…...

android 上位机调试软件-安卓串口 com ttl 调试——仙盟创梦IDE
在 Android 开发中,基于com.ttl库的串口调试 Web 编写意义非凡。它打破了硬件与软件之间的壁垒,让 Android 设备能够与外部串口设备通信。对于智能家居、工业控制等领域,这一功能使得手机或平板能成为控制终端,实现远程监控与操作…...

python打卡day42
Grad-CAM与Hook函数 知识点回顾 回调函数lambda函数hook函数的模块钩子和张量钩子Grad-CAM的示例 在深度学习中,我们经常需要查看或修改模型中间层的输出或梯度,但标准的前向传播和反向传播过程通常是一个黑盒,很难直接访问中间层的信息。PyT…...

XMOS以全新智能音频及边缘AI技术亮相广州国际专业灯光音响展
全球领先的边缘AI和智能音频解决方案提供商XMOS于5月27-30日亮相第23届广州国际专业灯光、音响展览会(prolight sound Guangzhou,以下简称“广州展”,XMOS展位号:5.2A66)。在本届展会上,XMOS将展出先进的音…...

Playwright 测试框架 - Node.js
🚀超全实战:基于 Playwright + Node.js 的自动化测试项目教程【附源码】 📌 本文适合自动化测试入门者 & 前端测试实战者。从零开始手把手教你搭建一个 Playwright + Node.js 项目,涵盖配置、测试用例编写、运行与调试、报告生成以及实用进阶技巧。建议收藏!👍 �…...

机器学习有监督学习sklearn实战二:六种算法对鸢尾花(Iris)数据集进行分类和特征可视化
本项目代码在个人github链接:https://github.com/KLWU07/Machine-learning-Project-practice 六种分类算法分别为逻辑回归LR、线性判别分析LDA、K近邻KNN、决策树CART、朴素贝叶斯NB、支持向量机SVM。 一、项目代码描述 1.数据准备和分析可视化 加载鸢尾花数据集&…...
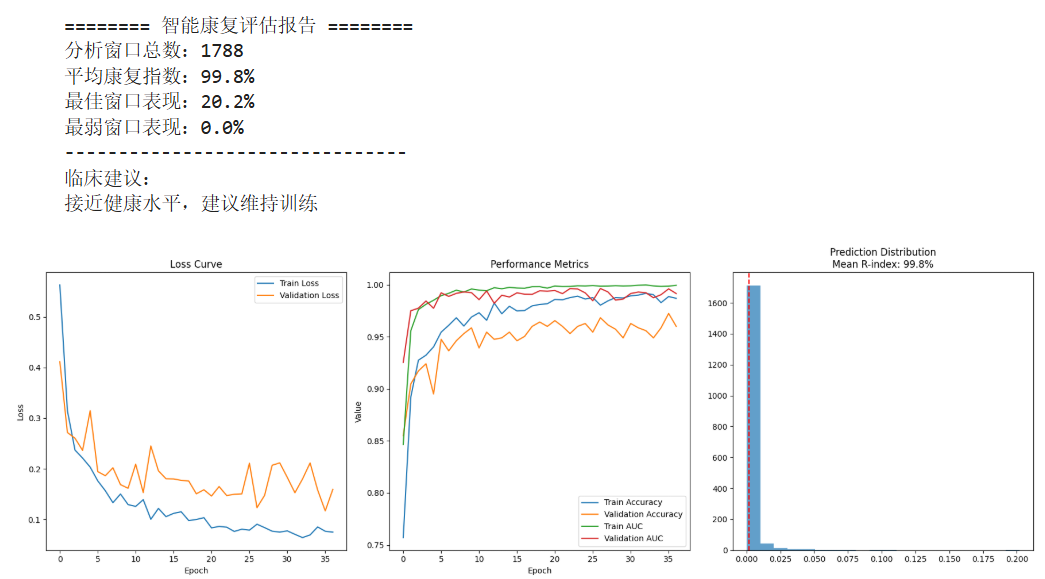
vr中风--数据处理模型搭建与训练2
位置http://localhost:8888/notebooks/Untitled1-Copy1.ipynb # -*- coding: utf-8 -*- """ MUSED-I康复评估系统(增强版) 包含:多通道sEMG数据增强、混合模型架构、标准化处理 """ import numpy as np impor…...

鸿蒙next系统以后会取代安卓吗?
点击上方关注 “终端研发部” 设为“星标”,和你一起掌握更多数据库知识 官方可没说过取代谁谁,三足鼎立不好吗?三分天下,并立共存。 鸿蒙基于Linux,有人说套壳;ios/macos基于Unix,说它ios开源了…...

PolyGen:一个用于 3D 网格的自回归生成模型 论文阅读
[2002.10880] PolyGen:一个用于 3D 网格的自回归生成模型 --- [2002.10880] PolyGen: An Autoregressive Generative Model of 3D Meshes 图 2:PolyGen 首先生成网格顶点(左侧),然后基于这些顶点生成网格面࿰…...

约瑟夫问题 洛谷 - P1996
Description n个人围成一圈,从第一个人开始报数,数到 m 的人出列,再由下一个人重新从 1 开始报数,数到 m 的人再出圈,依次类推,直到所有的人都出圈,请输出依次出圈人的编号。 注意:本题和《深…...

系统思考:成长与投资不足
最近认识了一位95后年轻创业者,短短2年时间,他的公司从十几个人发展到几百人,规模迅速扩大。随着团队壮大,用户池也在持续扩大,但令人困惑的是,业绩增长却没有明显提升,甚至人效持续下滑。尽管公…...

快手可灵视频V1.6模型API如何接入免费AI开源项目工具
全球领先的视频生成大模型:可灵是首个效果对标 Sora 、面向用户开放的视频生成大模型,目前在国内及国际上均处于领先地位。快手视频生成大模型“可灵”(Kling),是全球首个真正用户可用的视频生成大模型,自面…...

数学建模期末速成 最短路径
关键词:Dijkstra算法 Floyd算法 例题 已知有6个村庄,各村的小学生人数如表所列,各村庄间的距离如图所示。现在计划建造一所医院和一所小学,问医院应建在哪个村庄才能使最远村庄的人到医院看病所走的路最短?又问小学建…...

【Netty系列】实现HTTP文件服务器
目录 一、完整代码实现 1. Maven依赖 (pom.xml) 2. 主启动类 (FileServer.java) 3. 通道初始化类 (FileServerInitializer.java) 4. 核心业务处理器 (FileServerHandler.java) 二、代码关键解释 1. 架构分层 2. 安全防护机制 3. 文件传输优化 4. 目录列表生成 三、运…...
Java开发经验——阿里巴巴编码规范实践解析7
摘要 本文主要解析了阿里巴巴 Java 开发中的 SQL 编码规范,涉及 SQL 查询优化、索引建立、字符集选择、分页查询处理、外键与存储过程的使用等多个方面,旨在帮助开发者提高代码质量和数据库操作性能,避免常见错误和性能陷阱。 1. 【强制】业…...

权威认证与质量保障:第三方检测在科技成果鉴定测试中的核心作用
科技成果鉴定测试是衡量科研成果技术价值与应用潜力的关键环节,其核心目标在于通过科学验证确保成果的可靠性、创新性和市场适配性。第三方检测机构凭借其独立性、专业性和权威性,成为科技成果鉴定测试的核心支撑主体。本文从测试流程、第三方检测的价值…...

混和效应模型在医学分析中的应用
混合效应模型(Mixed Effects Model),又称多层模型或随机效应模型,因其能同时分析固定效应(群体平均趋势)和随机效应(个体或组间差异),在医学研究中广泛应用于处理具有层次…...

架构分享|三层存储架构加速云端大模型推理
作者简介 Nilesh Agarwal,Inferless 联合创始人&CTO 关于Inferless Inferless :无服务器 GPU 推理无需管理服务器即可扩展机器学习推理,轻松部署复杂的自定义模型。获得Sequoia、Antler 和 Blume Ventures 的支持。 大语言模型(LLM&a…...

Perforce P4产品简介:无限扩展+全球协作+安全管控+工具集成(附下载)
本产品简介由Perforce中国授权合作伙伴——龙智编辑整理,旨在带您快速了解Perforce P4版本控制系统的强大之处。 世界级无限可扩展的版本控制系统 Perforce P4(原Helix Core)是业界领先的版本控制平台,备受19家全球Top20 AAA级游…...

网络协议入门:TCP/IP五层模型如何实现全球数据传输?
🔍 开发者资源导航 🔍🏷️ 博客主页: 个人主页📚 专栏订阅: JavaEE全栈专栏 内容: 网络初识什么是网络?关键概念认识协议五元组 协议分层OSI七层模型TCP/IP五层(四层&…...

Docker安装Redis集群(3主3从+动态扩容、缩容)保姆级教程含踩坑及安装中遇到的问题解决
前言 部署集群前,我们需要先掌握Redis分布式存储的核心算法。了解这些算法能帮助我们在实际工作中做出合理选择,同时清晰认识各方案的优缺点。 一、分布式存储算法 我们通过一道大厂面试题来进行阐述。 如下:1-2亿条数据需要缓存ÿ…...

企业级 AI 开发新范式:Spring AI 深度解析与实践
一、Spring AI 的核心架构与设计哲学 1.1 技术定位与价值主张 Spring AI 作为 Spring 生态系统的重要组成部分,其核心使命是将人工智能能力无缝注入企业级 Java 应用。它通过标准化的 API 抽象和 Spring Boot 的自动装配机制,让开发者能够以熟悉的 Spr…...

如何用docker部署ELK?
环境: ELK 8.8.0 Ubuntu20.04 问题描述: 如何用docker部署ELK? 解决方案: 一、环境准备 (一)主机设置 安装 Docker Engine :版本需为 18.06.0 或更新。可通过命令 docker --version 检查…...

Redis最佳实践——安全与稳定性保障之高可用架构详解
全面详解 Java 中 Redis 在电商应用的高可用架构设计 一、高可用架构核心模型 1. 多层级高可用体系 #mermaid-svg-Ffzq72Onkv7wgNKQ {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-Ffzq72Onkv7wgNKQ .error-icon{f…...

【Python 算法零基础 4.排序 ⑥ 快速排序】
既有锦绣前程可奔赴,亦有往日岁月可回首 —— 25.5.25 选择排序回顾 ① 遍历数组:从索引 0 到 n-1(n 为数组长度)。 ② 每轮确定最小值:假设当前索引 i 为最小值索引 min_index。从 i1 到 n-1 遍历,若找到…...

Java面试实战:从Spring Boot到微服务与AI的全栈挑战
场景一:初步了解和基本技术问题 面试官:我们先从基础开始,谢先生,你能简单介绍一下你在Java SE上的经验吗? 谢飞机:当然!Java就像是我的老朋友,尤其是8和11版本。我用它们做过很多…...

Go 即时通讯系统:日志模块重构,并从main函数开始
重构logger 上次写的logger.go过于繁琐,有很多没用到的功能;重构后只提供了简洁的日志接口,支持日志轮转、多级别日志记录等功能,并采用单例模式确保全局只有一个日志实例 全局变量 var (once sync.Once // 用于实现…...

CppCon 2014 学习:Exception-Safe Coding
以下是你提到的内容(例如 “Exception-Safe Coding 理解” 和 “Easier to Read!” 等)翻译成中文并进一步解释: 承诺:理解异常安全(Exception-Safe Coding) 什么是异常安全? 异常安全是指&a…...

MYSQL MGR高可用
1,MYSQL MGR高可用是什么 简单来说,MySQL MGR 的核心目标就是:确保数据库服务在部分节点(服务器)发生故障时,整个数据库集群依然能够继续提供读写服务,最大限度地减少停机时间。 2. 核心优势 v…...
