[蓝桥杯]春晚魔术【算法赛】
目录
输入格式
输出格式
样例输入
样例输出
运行限制
解决思路
代码说明
复杂度分析
问题描述
在蓝桥卫视春晚的直播现场,魔术师小蓝表演了一个红包魔术。只见他拿出了三个红包,里边分别装有 A、B 和 C 个金币。而后,他挥动魔术棒,念动咒语“福禄寿喜财神到~”,对红包里的金币进行 NN 次变换。每次变换,每个红包的金币数量都会变成其他两个红包金币数量的乘积。
例如:
- 初始金币数量 A=2A=2,B=3B=3,C=5C=5,进行 N=1N=1 次变换后,金币数量变为 1515,1010,66。
- 初始金币数量 A=1A=1,B=2B=2,C=3C=3,进行 N=2N=2 次变换后,金币数量变为 66,1212,1818。
变换结束后,小蓝得意地问观众:“现在,你们知道三个红包里金币的总乘积是多少吗?” 他飞快地心算了一下,并报出一个数字:“让我来揭晓答案吧!总乘积是…嗯…(不知道算没算对,只知道算得快)”。
作为观众,请你计算 NN 次变换后,三个红包金币数量的总乘积。由于结果可能很大,请输出其对 109+7109+7 取模的结果。
输入格式
第一行包含一个整数 TT (1≤T≤103)(1≤T≤103),表示测试用例的数量。
接下来的 TT 行,每行包含四个整数 AA,BB,CC 和 NN(1≤A,B,C,N≤1091≤A,B,C,N≤109),表示一组数据。
输出格式
对于每组数据,输出一个整数,表示 NN 次变换后三个红包金币数量的总乘积。由于结果可能很大,请输出其对 109+7109+7 取模的结果。
样例输入
2
2 3 5 1
1 2 3 2
样例输出
900
1296
运行限制
| 语言 | 最大运行时间 | 最大运行内存 |
|---|---|---|
| C++ | 1s | 256M |
| C | 1s | 256M |
| Java | 2s | 256M |
| Python3 | 3s | 256M |
| PyPy3 | 3s | 256M |
| Go | 3s | 256M |
| JavaScript | 3s | 256M |
总通过次数: 342 | 总提交次数: 774 | 通过率: 44.2%
难度: 中等 标签: 欧拉降幂, 快速幂, 思维, 数学
解决思路
-
问题分析:每次变换,红包金币数量变为其他两个红包金币数量的乘积。经过数学推导,N次变换后的总乘积为 (𝐴×𝐵×𝐶)2𝑁mod (109+7)(A×B×C)2Nmod(109+7)。
-
关键观察:
-
初始总乘积 𝑆0=𝐴×𝐵×𝐶S0=A×B×C。
-
经过N次变换后,总乘积 𝑆𝑁=𝑆02𝑁SN=S02N。
-
-
处理大数:
-
使用模 𝑀=109+7M=109+7(质数),其欧拉函数 𝜙(𝑀)=𝑀−1=109+6ϕ(M)=M−1=109+6。
-
若 𝐴×𝐵×𝐶≡0mod 𝑀A×B×C≡0modM,则结果直接为0(因为后续幂运算仍为0)。
-
否则,计算指数 2𝑁mod 𝜙(𝑀)2Nmodϕ(M),再计算 𝑆0S0 的该指数次幂模 𝑀M。
-
-
高效计算:
-
使用快速幂算法计算模幂,时间复杂度 𝑂(log𝑁)O(logN) 和 𝑂(logexponent)O(logexponent)。
-
使用
__int128处理大数乘法中的溢出问题(适用于支持该类型的编译器)。
-
#include <iostream>
#include <cstdio>
using namespace std;const long long MOD = 1000000007;
const long long PHI = 1000000006; // MOD-1// 快速幂函数:计算 (base^exp) % mod
long long fast_pow(long long base, long long exp, long long mod) {if (exp == 0) {return 1 % mod; // 任何数的0次幂为1(模mod)}base %= mod;long long result = 1;while (exp > 0) {if (exp & 1) {result = (result * base) % mod;}base = (base * base) % mod;exp >>= 1;}return result;
}int main() {int T;scanf("%d", &T);while (T--) {long long A, B, C, N;scanf("%lld %lld %lld %lld", &A, &B, &C, &N);// 计算 base = (A * B * C) % MOD,使用 __int128 避免溢出long long a_mod = A % MOD;long long b_mod = B % MOD;long long c_mod = C % MOD;__int128 temp = static_cast<__int128>(a_mod) * b_mod;temp %= MOD;temp = temp * c_mod;temp %= MOD;long long base = static_cast<long long>(temp);// 若 base 为 0,则结果为 0if (base == 0) {printf("0\n");continue;}// 计算指数:exponent = 2^N mod PHIlong long exponent = fast_pow(2, N, PHI);// 计算结果:result = base^exponent mod MODlong long result = fast_pow(base, exponent, MOD);printf("%lld\n", result);}return 0;
}代码说明
-
常量定义:
-
MOD = 1000000007:取模基数。 -
PHI = 1000000006:欧拉函数值(MOD - 1)。
-
-
快速幂函数
fast_pow:-
高效计算 baseexpmod modbaseexpmodmod。
-
使用二进制分解将时间复杂度降至 𝑂(logexp)O(logexp)。
-
-
主函数:
-
读取测试用例数 𝑇T。
-
对每个测试用例:
-
读取 𝐴,𝐵,𝐶,𝑁A,B,C,N。
-
计算初始乘积模 𝑀𝑂𝐷MOD(使用
__int128避免中间结果溢出)。 -
若初始乘积模 𝑀𝑂𝐷MOD 为 0,则输出 0。
-
否则,计算指数 2𝑁mod PHI2NmodPHI,再计算最终结果 baseexponentmod MODbaseexponentmodMOD。
-
-
-
输入输出:
-
使用
scanf和printf提高效率。
-
复杂度分析
-
时间复杂度:每个测试用例执行两次快速幂运算(一次计算指数,一次计算结果),每次 𝑂(logexponent)O(logexponent)。总时间复杂度 𝑂(𝑇log𝑁)O(TlogN),满足 𝑇≤1000T≤1000 和 𝑁≤109N≤109 的限制。
-
空间复杂度:𝑂(1)O(1),仅使用常数空间。
相关文章:

[蓝桥杯]春晚魔术【算法赛】
目录 输入格式 输出格式 样例输入 样例输出 运行限制 解决思路 代码说明 复杂度分析 问题描述 在蓝桥卫视春晚的直播现场,魔术师小蓝表演了一个红包魔术。只见他拿出了三个红包,里边分别装有 A、B 和 C 个金币。而后,他挥动魔术棒&a…...

LeetCode - 965. 单值二叉树
目录 题目 深度优先搜索方法 正确的写法 题目 965. 单值二叉树 - 力扣(LeetCode) 深度优先搜索方法 什么是深度优先搜索:深度优先搜索(DFS)是一种图或树的遍历算法,它从起始节点开始,尽可能深地沿着一条路径探索&…...

LabVIEW杂草识别与精准喷洒
基于LabVIEW构建了一套集成机器视觉、智能决策与精准控制的农业杂草识别系统。通过高分辨率视觉传感器采集作物图像,利用 LabVIEW 的 NI Vision 模块实现图像颜色匹配与特征分析,结合 Arduino 兼容的工业级控制硬件,实现杂草定位与除草剂精准…...

分布式不同数据的一致性模型
1. 强一致性(Strong Consistency) 定义:所有节点在任何时间点看到的数据完全一致,读操作总是返回最近的写操作结果。特点: 写操作完成后,所有后续读操作都能立即看到更新。通常需要同步机制(如…...

“application/json“,“text/plain“ 分别表示什么
这两个字符串:“application/json” 和 “text/plain” 是 MIME 类型(媒体类型),用于告诉接收方消息内容的格式,它们出现在 ContentType 字段中。 它告诉系统或程序:“这段数据是什么格式?” 格…...
)
SQL: 窗口滑动(Sliding Window)
目录 什么是“窗口”? 什么是“滑动”? 🔍 滑动窗口的核心: 🕒 什么是时间窗口?(Time Window) 时间窗口的基本结构 时间窗口的三种常见形式 📊 什么是行窗口&…...

学习日记-day20-6.1
完成目标: 知识点: 1.集合_Collections集合工具类 方法:static <T> boolean addAll(Collection<? super T> c, T... elements)->批量添加元素 static void shuffle(List<?> list) ->将集合中的元素顺序打乱static <T>…...

【音视频】 FFmpeg 解码H265
一、概述 实现了使用FFmpeg读取对应H265文件,并且保存为对应的yuv文件 二、实现流程 读取文件 将H265/H264文件放在build路径下,然后指定输出为yuv格式 在main函数中读取外部参数 if (argc < 2){fprintf(stderr, "Usage: %s <input file&…...

Linux 系统 Docker Compose 安装
个人博客地址:Linux 系统 Docker Compose 安装 | 一张假钞的真实世界 本文方法是直接下载 GitHub 项目的 release 版本。项目地址:GitHub - docker/compose: Define and run multi-container applications with Docker。 执行以下命令将发布程序加载至…...

软件测试|FIT故障注入测试工具——ISO 26262合规下的智能汽车安全验证引擎
FIT(Fault Injection Tester)是SURESOFT专为汽车电子与工业控制设计的自动化故障注入测试工具,基于ISO 26262等国际安全标准开发,旨在解决传统测试中效率低、成本高、安全隐患难以复现的问题,其核心功能包括…...
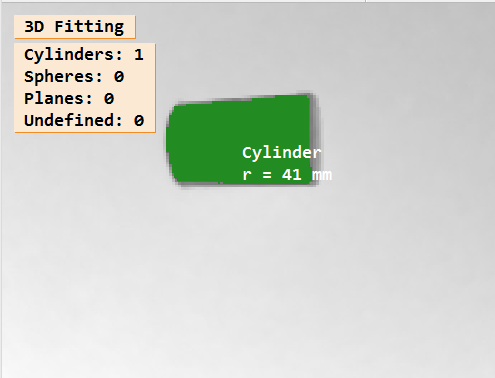
3D拟合测量水杯半径
1,目的。 测量水杯的半径 如图所示: 2,原理。 对 3D 点云对象 进行圆柱体拟合,获取拟合后的半径。 3,注意事项。 在Halcon中使用fit_primitives_object_model_3d进行圆柱体拟合时,输出的primitive_para…...
量子计算对密码学的影响)
(21)量子计算对密码学的影响
文章目录 2️⃣1️⃣ 量子计算对密码学的影响 🌌🔍 TL;DR🚀 量子计算:密码学的终结者?⚡ 量子计算的破坏力 🔐 Java密码学体系面临的量子威胁🔥 受影响最严重的Java安全组件 🛡️ 后…...

Python训练打卡Day38
Dataset和Dataloader类 知识点回顾: Dataset类的__getitem__和__len__方法(本质是python的特殊方法)Dataloader类minist手写数据集的了解 在遇到大规模数据集时,显存常常无法一次性存储所有数据,所以需要使用分批训练的…...

Selenium基础操作方法详解
Selenium基础操作方法详解:从零开始编写自动化脚本(附完整代码) 引言 Selenium是自动化测试和网页操作的利器,但对于新手来说,掌握基础操作是成功的第一步。本文将手把手教你使用Selenium完成浏览器初始化、元素定位、…...

Kali Linux从入门到实战:系统详解与工具指南
一、Kali Linux简介 Kali Linux是一款基于Debian的Linux发行版,专为渗透测试和网络安全审计设计,由Offensive Security团队维护。其前身是BackTrack,目前集成了超过600款安全工具,覆盖渗透测试全流程,是网络安全领域…...

【大模型】Bert变种
1. RoBERTa(Robustly optimized BERT approach) 核心改动 取消 NSP(Next Sentence Prediction)任务,研究发现 NSP 对多数下游任务贡献有限。动态遮蔽(dynamic masking):每个 epoch …...
)
vue-09(使用自定义事件和作用域插槽构建可重用组件)
实践练习:使用自定义事件和作用域插槽构建可重用组件 构建可重用的组件是高效 Vue.js 开发的基石。本课重点介绍如何通过自定义事件和范围插槽来增强组件的可重用性,从而实现更灵活和动态的组件交互。我们将探索如何定义和发出自定义事件,使…...

简单三步FastAdmin 开源框架的安装
简单三步FastAdmin 开源框架的安装 第一步:新建站点1,在宝塔面板中,创建一个新的站点,并填写项目域名。 第二步:上传框架1,框架下载2,上传解压缩 第三步:配置并安装1,进入…...

RISC-V 开发板 MUSE Pi Pro 搭建 Spacengine AI模型部署环境
视频讲解: RISC-V 开发板 MUSE Pi Pro 搭建 Spacengine AI模型部署环境 Spacengine 是由 进迭时空 研发的一套 AI 算法模型部署工具,可以方便的帮助用户部署自己的模型在端侧, 环境部署的方式,官方提供了两种方式: do…...

C++面试5——对象存储区域详解
C++对象存储区域详解 核心观点:内存是程序员的战场,存储区域决定对象的生杀大权!栈对象自动赴死,堆对象生死由你,全局对象永生不死,常量区对象只读不灭。 一、四大地域生死簿 栈区(Stack) • 特点:自动分配释放,速度极快(类似高铁进出站) • 生存期:函数大括号{}就…...

【Unity】AudioSource超过MaxDistance还是能听见
unity版本:2022.3.51f1c1 将SpatialBlend拉到1即可 或者这里改到0 Hearing audio outside max distance - #11 by wderstine - Questions & Answers - Unity Discussions...

基于 51 单片机的智能饮水机控制系统设计与实现
一、引言 随着物联网技术的发展,传统家电的智能化升级成为趋势。本文提出一种基于 51 单片机的智能饮水机设计方案,实现水温精准控制、水位监测、人机交互等功能,具有成本低、稳定性高的特点,适用于家庭和小型办公场景。 二、硬件设计 2.1 核心芯片选型 单片机:选用STC…...

Qt 读取和写入 INI 格式的配置文件
Qt 读取和写入 INI 格式的配置文件 前言:INI 配置文件在 Qt 开发中的重要性基础夯实:INI 文件结构与 QSettings 核心概念1. INI 文件的基本结构2. QSettings 类概述3. 初始化 QSettings 对象4. 基本读写操作5. 高级操作技巧5.1 处理数组和列表5.2 检查键…...

互联网大厂Java求职面试:AI与云原生架构实战解析
互联网大厂Java求职面试:AI与云原生架构实战解析 面试背景设定 场景:某互联网头部企业技术总监办公室,窗外是城市夜景,室内灯光柔和。面试官是一位经验丰富的技术总监,面前摆着一杯黑咖啡和候选人的简历。 候选人&a…...

Spring:从青铜到王者,你的Java修炼手册
一、Spring家族宇宙:原来你是这样的框架(青铜段位) 1.1 Spring的"前世今生":从泡面到满汉全席 2002年的泡面哲学:Rod Johnson在厨房煮泡面时突然顿悟:"Java开发为什么不能像泡面一…...

React和原生事件的区别
一、核心差异对比表 维度原生事件React 事件绑定语法HTML 属性(onclick)或 DOM API(addEventListener)JSX 中使用驼峰式属性(onClick)绑定位置直接绑定到具体 DOM 元素统一委托到根节点(React …...

Qt creator 设计页面控件认识与了解
记录一下 Qt 中的认识与了解: 在 Qt 中,这些功能属于 Qt Designer 的组件过滤系统,旨在帮助开发者在对象浏览器中快速定位和使用不同类型的控件和组件。以下是每个功能的详细讲解: Layouts(布局)&…...

命象架构法 02|你的系统有“用神”吗?
命理中说:“八字无用神,是虚命。” 系统架构中说:“模块无主线,是垃圾桶。” 你设计了无数类,却不知道哪个是核心。 那么你的系统,很可能是没有“用神”的。 01|什么是“用神”?不是你以为的“最好” 命理中,“用神”不是“最强的”,而是对命主最有帮助的。 比如一…...

NVIDIA Mellanox BlueField-2 DPU(Data Processing Unit)智能网卡的调试和使用
专有名词 OOB: BMC: BFB: EMMC: 关键词解释eMMCEmbedded Multi-Media Card——把 NAND 闪存颗粒与控制器封装在一起的板载存储件,类似手机里的“内置储存” .deb:文件是Debian软件包格式的专…...

Tomcat- AJP协议文件读取/命令执行漏洞(幽灵猫复现)详细步骤
一、漏洞描述 Apache Tomcat是由Apache软件基金会属下Jakarta项目开发的Servlet容器.默认情况下,Apache Tomcat会开启AJP连接器,方便与其他Web服务器通过AJP协议进行交互.但Apache Tomcat在AJP协议的实现上存在漏洞,导致攻击者可以通过发送恶意的AJP请求,可以读取或者包含Web应…...
