[蓝桥杯]上三角方阵
上三角方阵
题目描述
方阵的主对角线之上称为"上三角"。
请你设计一个用于填充 nn 阶方阵的上三角区域的程序。填充的规则是:使用 1,2,3.... 的自然数列,从左上角开始,按照顺时针方向螺旋填充。
例如:当 n=3n=3 时,输出:
1 2 3
6 4
5
当 n=4n=4 时,输出:
1 2 3 4
9 10 5
8 6
7
当 n=5n=5 时,输出:
1 2 3 4 5
12 13 14 6
11 15 7
10 8
9
输入描述
要求用户输入整数 n (3≤n≤20)n (3≤n≤20)。
输出描述
输出方阵的上三角部分。
要求每个数据宽度为 4,右对齐。
输入输出样例
示例
输入
9
输出
1 2 3 4 5 6 7 8 9
24 25 26 27 28 29 30 10
23 39 40 41 42 31 11
22 38 45 43 32 12
21 37 44 33 13
20 36 34 14
19 35 15
18 16
17
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
总通过次数: 832 | 总提交次数: 900 | 通过率: 92.4%
难度: 中等 标签: 2011, 模拟, 省赛
问题分析
题目要求设计一个程序,用自然数1, 2, 3,... 按顺时针螺旋顺序填充n阶方阵的上三角区域。上三角区域定义为方阵主对角线(含)以上的部分。填充后需按特定格式输出:每行数据宽度为4,右对齐,且输出为锯齿状矩阵(第i行有n-i个元素)。
算法思路
-
路径模拟:
- 使用方向数组控制螺旋路径:
右 (0,1)→左下 (1,-1)→上 (-1,0) - 从(0,0)开始,按优先级选择方向:先尝试当前方向,若无效则按
右→左下→上顺序切换 - 位置(r,c)有效条件:
- 在矩阵范围内:
0 ≤ r,c < n - 在上三角区域内:
c ≤ n - r - 1 - 目标位置未被填充
- 在矩阵范围内:
- 使用方向数组控制螺旋路径:
-
填充过程:
- 计算总元素数:
T = n(n+1)/2 - 初始化n×n矩阵,所有元素为0
- 从k=1到T,依次填充数字:
- 将当前值k赋给矩阵位置(r,c)
- 尝试三种方向,找到第一个有效移动位置
- 更新坐标(r,c)和当前方向
- 计算总元素数:
-
输出格式:
- 按锯齿状输出:第i行输出前
n-i个元素 - 每个元素占4字符宽度,右对齐(C++中
setw(4))#include <iostream> #include <vector> #include <iomanip> using namespace std;int main() {int n;cin >> n;int T = n * (n + 1) / 2; // 上三角区域总元素数vector<vector<int>> a(n, vector<int>(n, 0)); // 初始化n×n矩阵// 方向数组:右(0,1) -> 左下(1,-1) -> 上(-1,0)int dr[3] = {0, 1, -1};int dc[3] = {1, -1, 0};int r = 0, c = 0; // 起始位置(0,0)int current_dir = 0; // 初始方向:右for (int k = 1; k <= T; ++k) {a[r][c] = k; // 填充当前值if (k == T) break; // 填充完成bool found = false;for (int i = 0; i < 3; ++i) {int nd = (current_dir + i) % 3; // 尝试方向优先级:当前→下一→下下int nr = r + dr[nd];int nc = c + dc[nd];// 检查新位置是否有效if (nr >= 0 && nr < n && nc >= 0 && nc < n && nc <= n - nr - 1 && a[nr][nc] == 0) {r = nr;c = nc;current_dir = nd; // 更新方向found = true;break;}}if (!found) break; // 无有效位置(理论上不会发生)}// 输出锯齿状上三角矩阵for (int i = 0; i < n; ++i) {for (int j = 0; j < n - i; ++j) {cout << setw(4) << a[i][j];}cout << endl;}return 0; }关键步骤说明
-
方向控制:
- 右移:列坐标+1,用于填充当前行
- 左下移:行坐标+1且列坐标-1,用于斜向填充
- 上移:行坐标-1,用于填充左侧列
- 方向切换确保路径始终顺时针螺旋
-
边界检查:
- 矩阵边界:
0 ≤ r,c < n - 上三角边界:
c ≤ n - r - 1(确保不越出上三角区域) - 已填充检查:目标位置值为0
- 矩阵边界:
-
复杂度分析:
- 时间复杂度:O(n²),需填充n(n+1)/2个元素
- 空间复杂度:O(n²),存储n×n矩阵
- 满足运行限制(n≤20时,计算量远低于1s)
-
示例验证
输入n=3:
1 2 36 45路径轨迹:
- (0,0)→(0,1)→(0,2) // 右移填充顶边
- (1,1)→(2,0) // 左下移填充斜边
- (1,0) // 上移填充左边
-
输入n=4:
1 2 3 49 10 58 67路径轨迹:
- (0,0)→(0,1)→(0,2)→(0,3) // 右移
- (1,2)→(2,1)→(3,0) // 左下移
- (2,0)→(1,0) // 上移
- (1,1) // 右移
- 按锯齿状输出:第i行输出前
相关文章:

[蓝桥杯]上三角方阵
上三角方阵 题目描述 方阵的主对角线之上称为"上三角"。 请你设计一个用于填充 nn 阶方阵的上三角区域的程序。填充的规则是:使用 1,2,3.... 的自然数列,从左上角开始,按照顺时针方向螺旋填充。 例如&am…...

60天python训练计划----day44
DAY 44 预训练模型 知识点回顾: 预训练的概念常见的分类预训练模型图像预训练模型的发展史预训练的策略预训练代码实战:resnet18 一、预训练的概念 我们之前在训练中发现,准确率最开始随着epoch的增加而增加。随着循环的更新,参数…...
【JAVA版】意象CRM客户关系管理系统+uniapp全开源
一.介绍 CRM意象客户关系管理系统,是一个综合性的客户管理平台,旨在帮助企业高效地管理客户信息、商机、合同以及员工业绩。系统通过首页、系统管理、工作流程、审批中心、线索管理、客户管理、商机管理、合同管理、CRM系统、数据统计和系统配置等模块&…...
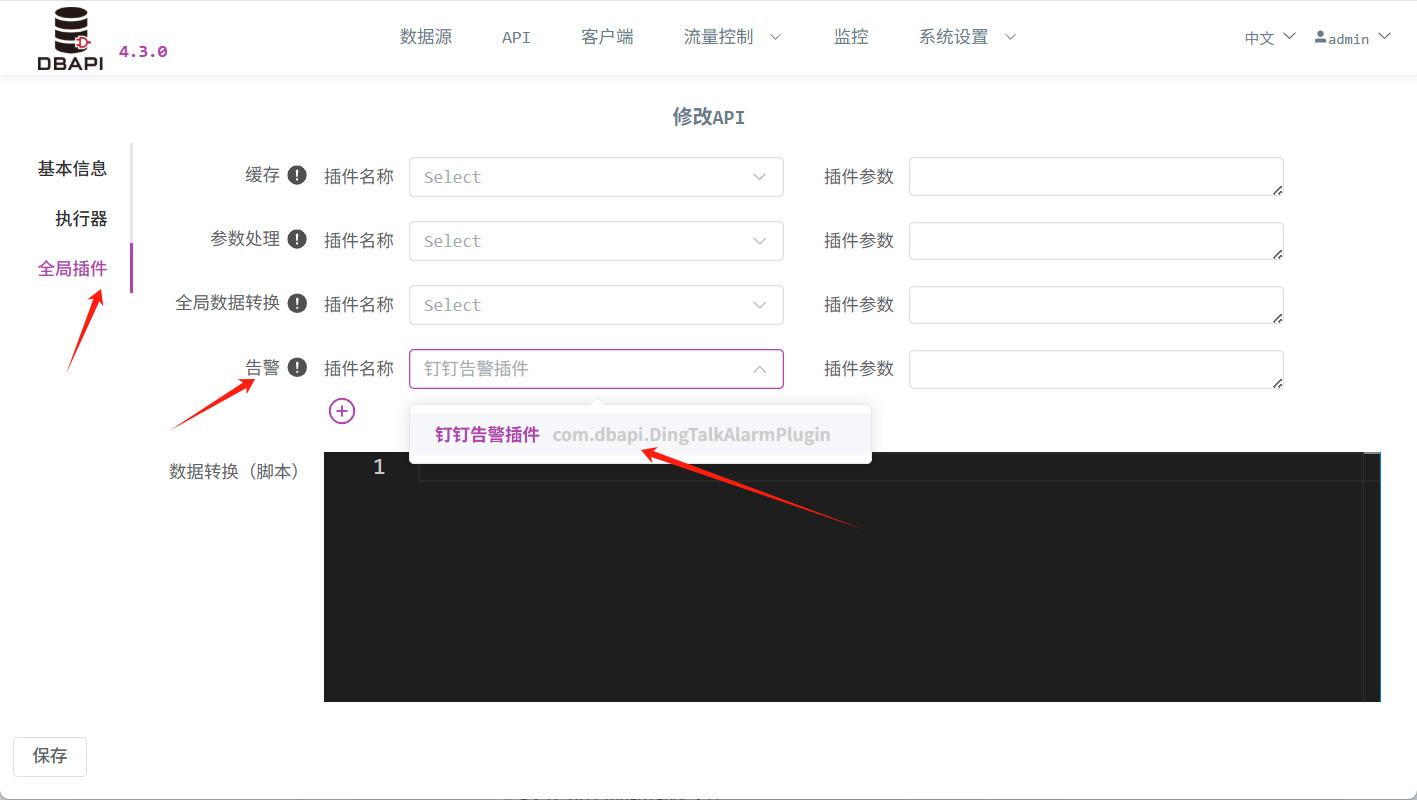
API异常信息如何实时发送到钉钉
#背景 对于一些重要的API,开发人员会非常关注API有没有报错,为了方便开发人员第一时间获取错误信息,我们可以使用插件来将API报错实时发送到钉钉群。 接下来我们就来实操如何实现 #准备工作 #创建钉钉群 如果已有钉钉群,可以跳…...

Python爬虫(48)基于Scrapy-Redis与深度强化学习的智能分布式爬虫架构设计与实践
目录 一、背景与行业痛点二、核心技术架构设计2.1 分布式爬虫基础架构2.2 深度强化学习模块 三、生产环境实践案例3.1 电商价格监控系统3.2 学术文献采集系统 四、高级优化技术4.1 联邦学习增强4.2 神经架构搜索(NAS) 五、总结🌈Python爬虫相…...

AtCoder Beginner Contest 407 E - Most Valuable Parentheses
AtCoder Beginner Contest 407 E - Most Valuable Parentheses E - Most Valuable Parentheses 反悔贪心算法 性质: 假设长度为 n n n, n ≡ 0 ( m o d 2 ) n \equiv 0 \pmod{2} n≡0(mod2) 的括号序列是合法的,那么有 n 2 \frac{n}{2}…...

(1-6-3)Java 多线程
目录 0.知识拓扑 1. 多线程相关概念 1.1 进程 1.2 线程 1.3 java 中的进程 与 线程概述 1.4 CPU、进程 与 线程的关系 2.多线程的创建方式 2.1 继承Thread类 2.2 实现Runnable接口 2.3 实现Callable接口 2.4 三种创建方式对比 3.线程同步 3.1 线程同步机制概述 …...

java31
1.网络编程 三要素: 网址实质上就是ip InetAddress: UDP通信程序: 多个接收端的地址都要加入同一个组播地址,这样发送端发信息,全部接收端都能接受到数据 广播的代码差不多,就是地址不一样而已 TCP通信程序…...

多模态之智能数字人
多模态下智能数字人的开发是一个复杂且系统性的工程,它融合了人工智能(AI)、计算机图形学、自然语言处理(NLP)、语音技术、计算机视觉(CV)等多个前沿领域。 多模态下智能数字人的开发流程规范 目标: 构建一个能够理解并生成多模态信息(文本、语音、视觉等),具备智…...

界面组件DevExpress WPF中文教程:Grid - 如何识别行和卡片?
DevExpress WPF拥有120个控件和库,将帮助您交付满足甚至超出企业需求的高性能业务应用程序。通过DevExpress WPF能创建有着强大互动功能的XAML基础应用程序,这些应用程序专注于当代客户的需求和构建未来新一代支持触摸的解决方案。 无论是Office办公软件…...

【HarmonyOS Next之旅】DevEco Studio使用指南(三十)
目录 1 -> 部署云侧工程 2 -> 通过CloudDev面板获取云开发资源支持 3 -> 通用云开发模板 3.1 -> 适用范围 3.2 -> 效果图 4 -> 总结 1 -> 部署云侧工程 可以选择在云函数和云数据库全部开发完成后,将整个云工程资源统一部署到AGC云端。…...

AI基础知识(LLM、prompt、rag、embedding、rerank、mcp、agent、多模态)
AI基础知识(LLM、prompt、rag、embedding、rerank、mcp、agent、多模态) 1、LLM大语言模型 --基于深度学习技术,通过海量文本数据训练而成的超大规模人工智能模型,能够理解、生成和推理自然语言文本 --产品&…...

[蓝桥杯]高僧斗法
高僧斗法 题目描述 古时丧葬活动中经常请高僧做法事。仪式结束后,有时会有"高僧斗法"的趣味节目,以舒缓压抑的气氛。 节目大略步骤为:先用粮食(一般是稻米)在地上"画"出若干级台阶(…...

pycharm F2 修改文件名 修改快捷键
菜单:File-> Setting, Keymap中搜索 Rename, 其中,有 Refactor-> Rename,右键添加快捷键,F2,删除原有快捷键就可以了。...

Python Flask中启用AWS Secrets Manager+AWS Parameter Store配置中心
问题 最近需要改造一个Python的Flask项目。需要在这个项目中添加AWS Secrets Manager作为配置中心,主要是数据库相关配置。 前提 得预先在Amazon RDS里面新建好数据库用户和数据库,以AWS Aurora为例子,建库和建用户语句类似如下࿱…...

机器学习与深度学习10-支持向量机02
目录 前文回顾6.如何构建SVM7.SVM与多分类问题8.SVM与逻辑回归9.SVM的可扩展性10.SVM的适用性和局限性 前文回顾 上一篇文章链接:地址 6.如何构建SVM 选择合适的核函数和超参数来构建支持向量机(SVM)模型通常需要一定的经验和实验。以下是…...

《深入解析UART协议及其硬件实现》-- 第二篇:UART硬件架构设计与FPGA实现
第二篇:UART硬件架构设计与FPGA实现 1. 模块化架构设计 1.1 系统级框图与时钟域划分 核心模块划分 : 发送模块(TX) :负责数据帧组装与串行输出。 接收模块(RX) :负责串行数据采样与…...

java swing 晃动鼠标改变背景颜色
import java.awt.Color; import java.awt.Component; import java.awt.event.MouseEvent; import java.awt.event.MouseMotionListener;import javax.swing.*; public class testA extends JFrame {testA(){super("晃动鼠标改变背景颜色");setBounds(600, 200, 600, …...

HikariCP 可观测性最佳实践
HikariCP 介绍 HikariCP 是一个高性能、轻量级的 JDBC 连接池,由 Brett Wooldridge 开发。它以“光”命名,象征快速高效。它支持多种数据库,配置简单,通过字节码优化和智能管理,实现低延迟和高并发处理。它还具备自动…...

简简单单探讨下starter
前言 今天其实首先想跟大家探讨下:微服务架构,分业务线了,接入第三方服务、包啥的是否自己定义一个stater更好? 一、starter是什么? 在 Spring Boot 中,Starter 是一种特殊的依赖模块,用于快速…...

PyTest框架学习
0. 优先查看学习教程 超棒的学习教程 1. yield 语句 yield ptc_udp_clientyield:在 Pytest fixture 中,yield 用于分隔设置和清理代码。yield 之前的代码在测试用例执行前运行,yield 之后的代码在测试用例执行后运行。ptc_udp_client&…...

SIP、SAP、SDP、mDNS、SSH、PTP
🌈 一、SIP 会话初始协议 会话初始协议 SIP 是一个在 IP 网络上进行多媒体通信的应用层控制协议,它被用来创建、修改和终结 1 / n 个参加者参加的会话进程。SIP 不能单独完成呼叫功能,需要和 RTP、SDP 和 DNS 配合来完成。 1. SIP 协议的功…...

【AI学习笔记】Coze工作流写入飞书多维表格(即:多维表格飞书官方插件使用教程)
背景前摇: 今天遇到一个需求,需要把Coze平台大模型和用户的对话记录保存进飞书表格,这个思路其实不难,因为官方提供了写入飞书表格和多维表格的插件,但是因为平台教程和案例的资料匮乏,依据现有的官方文档…...

System.Threading.Timer 和 System.Timers.Timer
在 .NET 中,System.Threading.Timer 和 System.Timers.Timer 都是用于定时任务的类,但它们的实现方式、使用场景和特性有所不同。以下是它们的 核心区别 和 使用示例: 1. System.Threading.Timer 特点 轻量级,基于线程池…...

在 Windows 系统下配置 VSCode + CMake + Ninja 进行 C++ 或 Qt 开发
在 Windows 系统下配置 VSCode CMake Ninja 进行 C 或 Qt 开发,是一个轻量级但功能强大的开发环境。下面我将分步骤详细说明如何搭建这个开发环境,支持纯 C 和 Qt 项目。 🧰 所需工具安装 1. 安装 Visual Studio Code(VSCode&…...

`tokenizer.decode` 出现乱码或异常输出,怎么处理
tokenizer.decode 出现乱码或异常输出,怎么处理 在使用 Hugging Face Transformers 库进行大语言模型(LLM)开发时,tokenizer.decode 出现乱码或异常输出,通常和模型输出的 token 序列、分词器对齐逻辑、特殊 token 处理有关。以下从模型侧、分词器侧、后处理环节给出解决…...

几何绘图与三角函数计算应用
几何绘图与三角函数计算应用 设计思路 左侧为绘图控制面板,右侧为绘图区域支持绘制点、线、矩形、圆、多边形等基本几何图形实现三角函数计算器(正弦、余弦、正切等)包含角度/弧度切换和常用数学常数历史记录功能保存用户绘图 完整实现代码…...

leetcode 二叉搜索树中第k小的元素 java
中序遍历 定义一个栈,用于存取二叉树中的元素 Deque<TreeNode> stack new ArrayDeque<TreeNode>();进入while循环while(! stack.isEmpty()|| root ! null){}将root的左节点入栈,直到rootnull while(rootnull){stack.push(root);root ro…...

5.1 初探大数据流式处理
在本节中,我们深入探讨了大数据流式处理的基础知识和关键技术。首先,我们区分了批式处理和流式处理两种大数据处理方式,了解了它们各自的适用场景和特点。流式处理以其低延迟和高实时性适用于需要快速响应的场景,而批式处理则适用…...

基于 Android 和 JBox2D 的简单小游戏
以下是一个基于 Android 和 JBox2D 的简单小游戏开发示例,实现一个小球在屏幕上弹跳的效果: 1. 添加 JBox2D 依赖 在项目的 build.gradle 文件中添加 JBox2D 的依赖: dependencies {implementation org.jbox2d:jbox2d-library:2.3.1 } 2.…...
