Bresenham算法
一 Bresenham 绘直线
使用 Bresenham 算法,可以在显示器上绘制一直线段。该算法主要思想如下:
1 给出直线段上两个端点
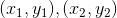
,根据端点求出直线在X,Y方向上变化速率
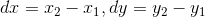
;
2 当
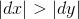
时,X 方向上变化速率快于 Y 方向上变化速率,选择在 X 方向上迭代,在每次迭代中计算 Y 轴上变化;
当

时,Y 方向上变化速率快于 X 方向上变化速率,选择在 Y 方向上迭代,在每次迭代中计算 X 轴上变化;
3 现在仅考虑

情形,在
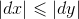
情况下仅需要交换变量即可。直线斜率
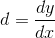
,当 d = 0 时,为一条水平直线,当 d > 0 或 d < 0 时,需要分开讨论,如下图:

二 Bresenham 绘圆
使用 Bresenham 绘制圆形,只需要绘制四分之一圆即可,其他部分通过翻转图形即可得到。假设圆心位于 (0, 0) 点,半径为 R,绘制第一象限四分之一圆形,如下图:
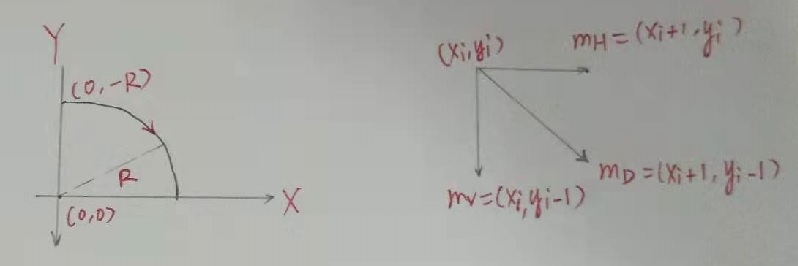
根据图形可知,从

出发,下一个可能的选择分别为:
1)水平方向上
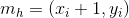
;
2)对角方向上
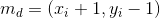
;
3)垂直方向上

;
下面计算

,根据差值可判断大致圆弧位置:
1)当

时,圆环落在

与

之间,进一步计算圆弧到

与

的距离以判断应该落在哪个点上;
2)

,
由于

,
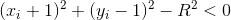
,上式可化简为,

,将

改写为

得:

,
已知
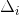
,可根据上式快速求解出
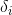
,当

时,下一点落在

上,当
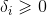
时,下一点落在

上;
3)当
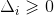
时,圆环落在

与

之间,进一步计算圆弧到

和

的距离以判断应该落在哪个点上;
4)

,可化简为:

,将

改写为
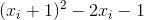
得:
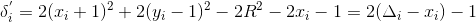
,
已知
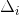
,可根据上式快速求解出
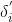
,当
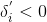
时,下一点落在

上,当
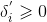
时,下一点落在
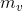
上;
5)以上推导中,已知

可以快速求解
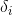
,同时,已知

也可以快速推导出

,以下分类讨论:
a. 当
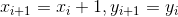
时,有:
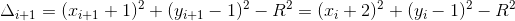
,进一步整理得:
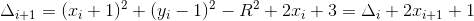
;
b. 当

时,有:
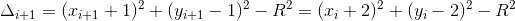
,进一步整理得:
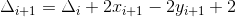
;
c. 当
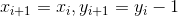
时,有:

,进一步整理得:

。
以下给出 Bresenham 绘圆实现:

1 void Bresenham_Circle(PairS center, int radius, std::vector<PairS>& circle)2 {3 PairS start(0, radius);4 int Delta = (start.x + 1) * (start.x + 1) +5 (start.y - 1) * (start.y - 1) - radius * radius;6 7 std::vector<PairS> tmp;8 tmp.push_back(start);9
10 while (start.y > 0)
11 {
12 int state = -1;
13
14 if (Delta < 0)
15 {
16 int delta = (Delta + start.y) * 2 - 1;
17 if (delta < 0)
18 {
19 start.x += 1;
20 state = 0;
21 }
22 else
23 {
24 start.x += 1;
25 start.y -= 1;
26 state = 1;
27 }
28 }
29 else
30 {
31 int delta = (Delta - start.x) * 2 - 1;
32 if (delta < 0)
33 {
34 start.x += 1;
35 start.y -= 1;
36 state = 1;
37 }
38 else
39 {
40 start.y -= 1;
41 state = 2;
42 }
43 }
44
45 if (state == 0)
46 Delta = Delta + start.x * 2 + 1;
47 else if (state == 1)
48 Delta = Delta + start.x * 2 - start.y * 2, +2;
49 else if (state == 2)
50 Delta = Delta - start.y * 2 + 1;
51 else
52 break;
53
54 tmp.push_back(start);
55 }
56
57 std::vector<PairS> tmp2;
58 for (int i = 0; i < tmp.size(); ++i)
59 {
60 PairS p(tmp[i].x, tmp[i].y);
61 tmp2.push_back(p);
62 }
63 for (int i = tmp.size() - 1; i >= 0; --i)
64 {
65 PairS p(tmp[i].x, -tmp[i].y);
66 tmp2.push_back(p);
67 }
68 for (int i = 0; i < tmp2.size(); ++i)
69 {
70 PairS p(tmp2[i].x, tmp2[i].y);
71 circle.push_back(p);
72 }
73
74 for (int i = tmp2.size() - 1; i >= 0; --i)
75 {
76 PairS p(-tmp2[i].x, tmp2[i].y);
77 circle.push_back(p);
78 }
79
80 for (int i = 0; i < circle.size(); ++i)
81 {
82 circle[i].x += center.x;
83 circle[i].y += center.y;
84 }
85 }

相关文章:

Bresenham算法
一 Bresenham 绘直线 使用 Bresenham 算法,可以在显示器上绘制一直线段。该算法主要思想如下: 1 给出直线段上两个端点 ,根据端点求出直线在X,Y方向上变化速率 ; 2 当 时,X 方向上变化速率快于 Y 方向上变化速率&am…...

【从GEO数据库批量下载数据】
从GEO数据库批量下载数据 1:进入GEO DataSets拿到所需要下载的数据的srr.list,上传到linux, 就可以使用prefetch这个函数来下载 2:操作步骤如下: conda 安装sra-tools conda create -n sra-env -c bioconda -c co…...

day 44
使用DenseNet预训练模型对cifar10数据集进行训练 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms, models from torch.utils.data import DataLoader import matplotlib.pyplot as plt import os# 设置中文字体…...

鸿蒙OSUniApp开发跨平台AR扫描识别应用:HarmonyOS实践指南#三方框架 #Uniapp
UniApp开发跨平台AR扫描识别应用:HarmonyOS实践指南 前言 随着增强现实(AR)技术在移动应用中的广泛应用,越来越多的开发者需要在跨平台应用中实现AR功能。本文将深入探讨如何使用UniApp框架开发一个高性能的AR扫描识别应用&…...

NER实践总结,记录一下自己实践遇到的各种问题。
更。 没卡,跑个模型休息好几天,又闲又急。 一开始直接套用了别人的代码进行实体识别,结果很差,原因是他的词表没有我需要的东西,我是用的医学文本。代码直接在github找了改的,用的是BERT的Chinese版本。 然…...

微信小程序实现运动能耗计算
微信小程序实现运动能耗计算 近我做了一个挺有意思的微信小程序,能够实现运动能耗的计算。只需要输入性别、年龄、体重、运动时长和运动类型这些信息,就能算出对应的消耗热量。 具体来说,在小程序里,性别不同,身体基…...

iTunes 无法备份 iPhone:10 种解决方法
Apple 设备是移动设备市场上最先进的产品之一,但有些人遇到过 iTunes 因出现错误而无法备份 iPhone 的情况。iTunes 拒绝备份 iPhone 时,可能会令人非常沮丧。不过,幸运的是,我们有 10 种有效的方法可以解决这个问题。您可以按照以…...

施耐德特价型号伺服电机VIA0703D31A1022、常见故障
⚙️ 一、启动类故障 电机无法启动 可能原因:电源未接通、制动器未释放、接线错误或控制器故障。解决措施: 检查电源线路及断路器状态;验证制动器是否打开(带制动器型号);核对电机与控制器…...

LangChain4J 使用实践
这里写目录标题 大模型应用场景:创建一个测试示例AIService聊天记忆实现简单实现聊天记录记忆MessageWindowChatMemory实现聊天记忆 隔离聊天记忆聊天记忆持久化 添加AI提示词 大模型应用场景: 创建一个测试示例 导入依赖 <dependency><groupI…...
:大表查询)
慢SQL调优(二):大表查询
最近在工作中写SQL出现几次慢SQL的BUG,总结下来归根到底就是因为大表的原因~这表有多大呢,执行 select COUNT(1) FROM position 是出不来结果滴,每天保底新增1000条数据,可想而知有多大了,所以多次踩坑了这张表。所以…...

【C++】—— 从零开始封装 Map 与 Set:实现与优化
人生的态度是,抱最大的希望,尽最大的努力,做最坏的打算。 —— 柏拉图 《理想国》 目录 1、理论基石——深度剖析 BSTree、AVLTree 与 RBTree 的概念区别 2、迭代器机制——RBTree 迭代器的架构与工程实现 3、高级容器设计——Map 与 Set…...

内网穿透之Linux版客户端安装(神卓互联)
选择Linux系统版本 获取安装包 :https://www.shenzhuohl.com/download.html 这里以Ubuntu 18.04为例,其它版本方法类似 登录Ubuntu操作系统: 打开Ubuntu系统终端,更新版本 apt-get update 安装运行环境: 安装C 运…...

开疆智能Profinet转Profibus网关连接CMDF5-8ADe分布式IO配置案例
本案例是客户通过开疆智能研发的Profinet转Profibus网关将PLC的Profinet协议数据转换成IO使用的Profibus协议,操作步骤如下。 配置过程: Profinet一侧设置 1. 打开西门子组态软件进行组态,导入网关在Profinet一侧的GSD文件。 2. 新建项目并…...

华为云Flexus+DeepSeek征文|Flexus云服务器单机部署+CCE容器高可用部署快速搭建生产级的生成式AI应用
前引: 在AI技术高速演进的浪潮中,如何快速、高效、安全地搭建一个大模型应用平台,成为开发者和企业关注的焦点。近日,华为云推出的Flexus云服务器配合CCE容器引擎和Dify LLM应用开发平台,带来了极具吸引力的解决方案。…...

扫地机产品--材质传感器算法开发与虚拟示波器
扫地机产品–材质传感器算法开发与虚拟示波器 文章目录 扫地机产品--材质传感器算法开发与虚拟示波器**一、材质传感器的工作原理**二、核心功能与应用场景三、技术参数与产品示例四.MCU 与压电陶瓷超声波的材质检测技术方案实现原理分析4.1 超声波原理4.2表面类型检测4.3 超声…...

[蓝桥杯]上三角方阵
上三角方阵 题目描述 方阵的主对角线之上称为"上三角"。 请你设计一个用于填充 nn 阶方阵的上三角区域的程序。填充的规则是:使用 1,2,3.... 的自然数列,从左上角开始,按照顺时针方向螺旋填充。 例如&am…...

60天python训练计划----day44
DAY 44 预训练模型 知识点回顾: 预训练的概念常见的分类预训练模型图像预训练模型的发展史预训练的策略预训练代码实战:resnet18 一、预训练的概念 我们之前在训练中发现,准确率最开始随着epoch的增加而增加。随着循环的更新,参数…...
【JAVA版】意象CRM客户关系管理系统+uniapp全开源
一.介绍 CRM意象客户关系管理系统,是一个综合性的客户管理平台,旨在帮助企业高效地管理客户信息、商机、合同以及员工业绩。系统通过首页、系统管理、工作流程、审批中心、线索管理、客户管理、商机管理、合同管理、CRM系统、数据统计和系统配置等模块&…...
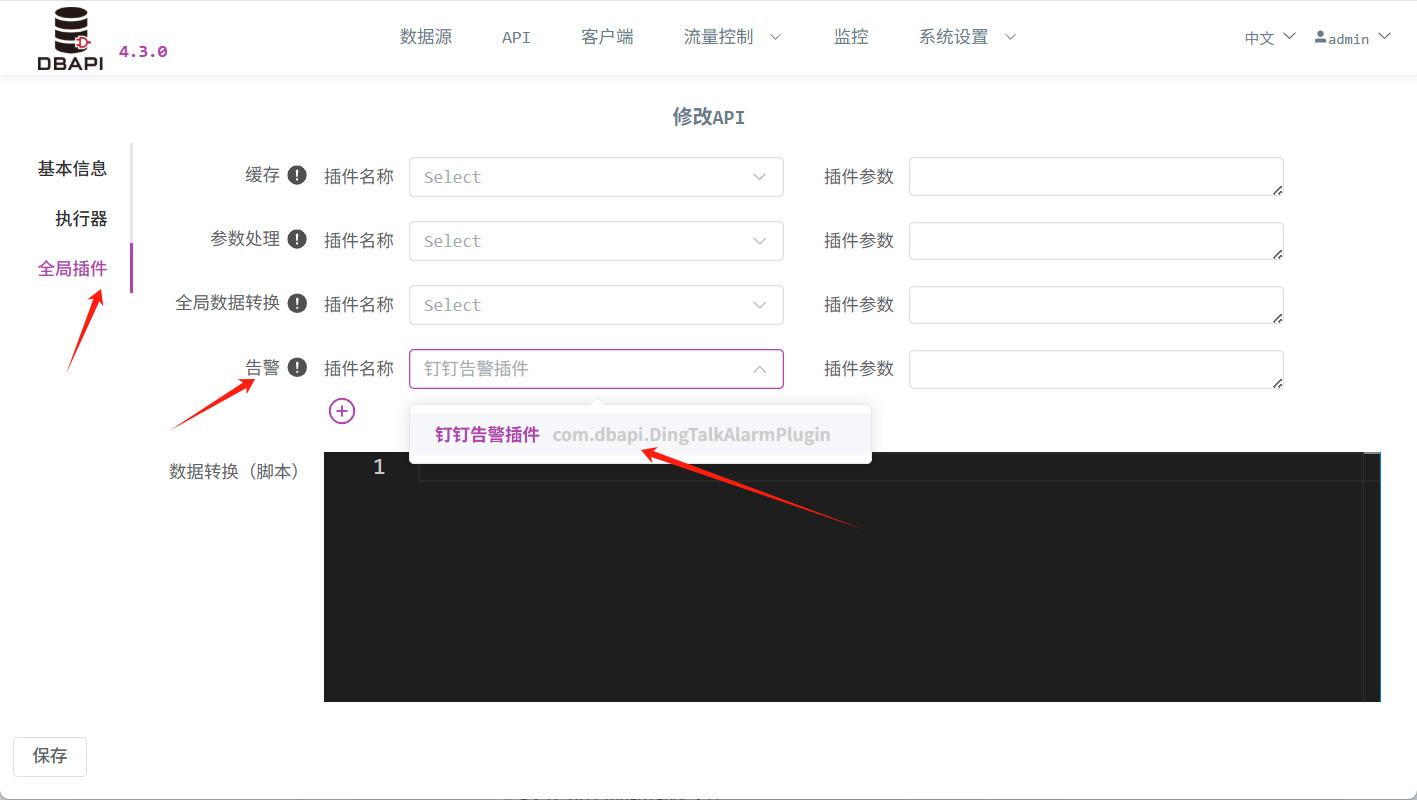
API异常信息如何实时发送到钉钉
#背景 对于一些重要的API,开发人员会非常关注API有没有报错,为了方便开发人员第一时间获取错误信息,我们可以使用插件来将API报错实时发送到钉钉群。 接下来我们就来实操如何实现 #准备工作 #创建钉钉群 如果已有钉钉群,可以跳…...

Python爬虫(48)基于Scrapy-Redis与深度强化学习的智能分布式爬虫架构设计与实践
目录 一、背景与行业痛点二、核心技术架构设计2.1 分布式爬虫基础架构2.2 深度强化学习模块 三、生产环境实践案例3.1 电商价格监控系统3.2 学术文献采集系统 四、高级优化技术4.1 联邦学习增强4.2 神经架构搜索(NAS) 五、总结🌈Python爬虫相…...

AtCoder Beginner Contest 407 E - Most Valuable Parentheses
AtCoder Beginner Contest 407 E - Most Valuable Parentheses E - Most Valuable Parentheses 反悔贪心算法 性质: 假设长度为 n n n, n ≡ 0 ( m o d 2 ) n \equiv 0 \pmod{2} n≡0(mod2) 的括号序列是合法的,那么有 n 2 \frac{n}{2}…...

(1-6-3)Java 多线程
目录 0.知识拓扑 1. 多线程相关概念 1.1 进程 1.2 线程 1.3 java 中的进程 与 线程概述 1.4 CPU、进程 与 线程的关系 2.多线程的创建方式 2.1 继承Thread类 2.2 实现Runnable接口 2.3 实现Callable接口 2.4 三种创建方式对比 3.线程同步 3.1 线程同步机制概述 …...

java31
1.网络编程 三要素: 网址实质上就是ip InetAddress: UDP通信程序: 多个接收端的地址都要加入同一个组播地址,这样发送端发信息,全部接收端都能接受到数据 广播的代码差不多,就是地址不一样而已 TCP通信程序…...

多模态之智能数字人
多模态下智能数字人的开发是一个复杂且系统性的工程,它融合了人工智能(AI)、计算机图形学、自然语言处理(NLP)、语音技术、计算机视觉(CV)等多个前沿领域。 多模态下智能数字人的开发流程规范 目标: 构建一个能够理解并生成多模态信息(文本、语音、视觉等),具备智…...

界面组件DevExpress WPF中文教程:Grid - 如何识别行和卡片?
DevExpress WPF拥有120个控件和库,将帮助您交付满足甚至超出企业需求的高性能业务应用程序。通过DevExpress WPF能创建有着强大互动功能的XAML基础应用程序,这些应用程序专注于当代客户的需求和构建未来新一代支持触摸的解决方案。 无论是Office办公软件…...

【HarmonyOS Next之旅】DevEco Studio使用指南(三十)
目录 1 -> 部署云侧工程 2 -> 通过CloudDev面板获取云开发资源支持 3 -> 通用云开发模板 3.1 -> 适用范围 3.2 -> 效果图 4 -> 总结 1 -> 部署云侧工程 可以选择在云函数和云数据库全部开发完成后,将整个云工程资源统一部署到AGC云端。…...

AI基础知识(LLM、prompt、rag、embedding、rerank、mcp、agent、多模态)
AI基础知识(LLM、prompt、rag、embedding、rerank、mcp、agent、多模态) 1、LLM大语言模型 --基于深度学习技术,通过海量文本数据训练而成的超大规模人工智能模型,能够理解、生成和推理自然语言文本 --产品&…...

[蓝桥杯]高僧斗法
高僧斗法 题目描述 古时丧葬活动中经常请高僧做法事。仪式结束后,有时会有"高僧斗法"的趣味节目,以舒缓压抑的气氛。 节目大略步骤为:先用粮食(一般是稻米)在地上"画"出若干级台阶(…...

pycharm F2 修改文件名 修改快捷键
菜单:File-> Setting, Keymap中搜索 Rename, 其中,有 Refactor-> Rename,右键添加快捷键,F2,删除原有快捷键就可以了。...

Python Flask中启用AWS Secrets Manager+AWS Parameter Store配置中心
问题 最近需要改造一个Python的Flask项目。需要在这个项目中添加AWS Secrets Manager作为配置中心,主要是数据库相关配置。 前提 得预先在Amazon RDS里面新建好数据库用户和数据库,以AWS Aurora为例子,建库和建用户语句类似如下࿱…...
