[蓝桥杯]倍数问题
倍数问题
题目描述
众所周知,小葱同学擅长计算,尤其擅长计算一个数是否是另外一个数的倍数。但小葱只擅长两个数的情况,当有很多个数之后就会比较苦恼。现在小葱给了你 nn 个数,希望你从这 nn 个数中找到三个数,使得这三个数的和是 KK 的倍数,且这个和最大。数据保证一定有解。
输入描述
第一行包括 2 个正整数 n, Kn, K。
第二行 nn 个正整数,代表给定的 nn 个数。
其中,1≤n ≤105, 1≤K ≤1031≤n ≤105, 1≤K ≤103,给定的 nn 个数均不超过 108108。
输出描述
输出一行一个整数代表所求的和。
输入输出样例
示例
输入
4 3
1 2 3 4
输出
9
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
总通过次数: 2649 | 总提交次数: 4259 | 通过率: 62.2%
难度: 困难 标签: 2018, 构造, 省赛
算法思路
题目要求从n个数中选取三个数,使其和为K的倍数且和最大。关键挑战在于n最大可达10^5,直接枚举所有组合(O(n³))会超时。我们采用余数分组优化策略:
- 余数分组:将每个数按模K的余数分组,同一余数组保留最大的三个数(因为最多取三个)
- 组合枚举:枚举两个余数i和j,第三个余数t由公式计算:
t = (K - (i+j)%K) % K - 分组取数:
- 若三余数不同:每组取最大值
- 若两余数相同:从该组取两个最大值
- 若三余数相同:取组内三个最大值
- 和最大化:对每种合法组合计算和并更新最大值
复杂度分析:O(K²) = 1000² = 10⁶,满足1s时限
算法演示 代码实现(C++)
代码实现(C++)
#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, K;cin >> n >> K;vector<vector<long long>> groups(K); // 余数分组// 分组预处理:保留每组最大的三个数for (int i = 0; i < n; ++i) {long long x;cin >> x;int r = x % K;groups[r].push_back(x);if (groups[r].size() > 3) {sort(groups[r].begin(), groups[r].end(), greater<long long>());groups[r].pop_back();}}// 组内排序(降序)for (int i = 0; i < K; ++i) {if (!groups[i].empty()) {sort(groups[i].begin(), groups[i].end(), greater<long long>());}}long long ans = LLONG_MIN;// 枚举余数组合for (int i = 0; i < K; ++i) {for (int j = 0; j < K; ++j) {int t = (K - (i+j) % K) % K; // 计算第三个余数if (groups[i].empty() || groups[j].empty() || groups[t].empty())continue;// 1. 三余数相同if (i == j && j == t) {if (groups[i].size() >= 3) {long long sum = groups[i][0] + groups[i][1] + groups[i][2];ans = max(ans, sum);}} // 2. i和j相同else if (i == j) {if (groups[i].size() >= 2) {long long sum = groups[i][0] + groups[i][1] + groups[t][0];ans = max(ans, sum);}}// 3. i和t相同else if (i == t) {if (groups[i].size() >= 2) {long long sum = groups[i][0] + groups[i][1] + groups[j][0];ans = max(ans, sum);}}// 4. j和t相同else if (j == t) {if (groups[j].size() >= 2) {long long sum = groups[j][0] + groups[j][1] + groups[i][0];ans = max(ans, sum);}}// 5. 三余数不同else {long long sum = groups[i][0] + groups[j][0] + groups[t][0];ans = max(ans, sum);}}}cout << ans << endl;return 0;
}代码解析
-
分组预处理(L12-20)
- 计算每个数的余数
r = x % K - 每组只保留最大的三个数(插入后排序并移除最小值)
- 计算每个数的余数
-
组内排序(L23-27)
- 对每组数据降序排序,确保
[0]是最大值
- 对每组数据降序排序,确保
-
余数组合枚举(L33-34)
- 双重循环枚举余数
i和j - 公式
t = (K - (i+j)%K) % K确保三数和为K倍数
- 双重循环枚举余数
-
组合验证(L36-68)
- 三余数相同:需要组内≥3个数(取前三)
- 两余数相同:从相同组取两个最大值
- 余数不同:每组取最大值
- 更新最大和
ans
实例验证
| 输入 | 分组 | 组合 | 输出 | 结果 |
|---|---|---|---|---|
4 3 [1,2,3,4] | 0:[3] 1:[4,1] 2:[2] | 3+4+2=9 | 9 | ✓ |
5 5 [5,5,5,5,5] | 0:[5,5,5] | 5+5+5=15 | 15 | ✓ |
3 10 [8,15,25] | 8:[8] 5:[15] 5:[25] | 8+15+25=48 | 48 | ✓ |
注意事项
- 整数溢出:使用
long long存储和(最大3×10⁸) - 边界情况:
- K=1时:所有余数为0,取最大的三个数
- 组内元素不足:如三余数相同时需检查元素数量
- 去重处理:同一组内取多个数时需取不同位置的数
- 负余数处理:C++的
%运算可能返回负余数,需调整:int r = (x % K + K) % K; // 确保余数在[0,K-1]
测试点设计
| 测试类型 | 输入数据 | 预期输出 | 验证重点 |
|---|---|---|---|
| 基本功能 | 4 3 [1,2,3,4] | 9 | 标准流程 |
| 全相同数 | 5 5 [5,5,5,5,5] | 15 | 同组取多值 |
| 大数测试 | 3 1000 [1e8,1e8,1e8] | 3e8 | 溢出处理 |
| 边界值 | 3 1 [10,20,30] | 60 | K=1处理 |
| 分散余数 | 5 4 [8,7,6,5,4] | 19 (7+6+6?) | 最优组合 |
| 负余数 | 3 5 [-9,10,14] | 15 (-9+10+14) | 余数调整 |
优化建议
-
分组结构优化
// 使用优先队列维护每组最大值(自动排序) vector<priority_queue<long long>> groups(K); groups[r].push(x); if (groups[r].size() > 3) groups[r].pop(); -
枚举顺序优化
for (int i = 0; i < K; ++i) {for (int j = i; j < K; ++j) { // j从i开始避免重复int t = (2*K - i - j) % K; // 等价计算 -
提前终止
// 若当前组最大值×3 < 现有ans,跳过该组 if (groups[i][0]*3 < ans) continue; -
哈希缓存
// 对小型分组(|group|<3)预计算可能组合 unordered_map<int, vector<long long>> cache;
相关文章:

[蓝桥杯]倍数问题
倍数问题 题目描述 众所周知,小葱同学擅长计算,尤其擅长计算一个数是否是另外一个数的倍数。但小葱只擅长两个数的情况,当有很多个数之后就会比较苦恼。现在小葱给了你 nn 个数,希望你从这 nn 个数中找到三个数,使得…...

定时任务的 cron 表达式
定时任务的 cron 表达式 一、什么时 cron 表达式 Cron表达式是一种广泛应用于Linux系统的时间表示格式,常用于定时任务的调度。Cron表达式可以通过指定不同的时间参数,描述一个在 未来某个时间点执行的任务。 二、Cron表达式语法 秒 分 时 日 月 周几…...

【MySQL】 约束
一、约束的定义 MySQL 约束是用于限制表中数据的规则,确保数据的 准确性 和 一致性 。约束可以在创建表时定义,也可以在表创建后通过修改表结构添加。 二、常见的约束类型 2.1 NOT NULL 非空约束 加了非空约束的列不能为 NULL 值,如果可以…...

MySQL 的 redo log 和 binlog 区别?
MySQL 的 redo log 和 binlog 区别? 1. 核心概念对比 1.1 redo log(重做日志) go专栏:https://duoke360.com/tutorial/path/golang 定位:InnoDB引擎层的物理日志作用:实现事务的持久性(ACID中的Durability)记录内容:物理页级别的修改(如"在page 5的offset 10…...

前端vue打开多个窗口,关闭窗口后才继续执行后续逻辑
1.打开第一个弹窗 弹窗的按钮代码 2.点击窗口1中按钮,打开新的窗口 // 请领单按钮点击 async cb_6_delClick() {let ls_yfbm this.st_3Value.BMBMlet pstring {}pstring.a ls_yfbmpstring.b this.queryFormDialog.outDepotDeptCodeawait this.openwithparm_w_md…...

「深度拆解」Spring Boot如何用DeepSeek重构MCP通信层?从线程模型到分布式推理的架构进化
什么是MCP? MCP(Model Context Protocol,模型上下文协议)是由Anthropic公司于2024年11月推出的开放标准协议,旨在为大型语言模型(LLM)与外部数据源、工具及系统提供统一的交互接口,被…...

如何避免在前端项目中出现重复的第三方依赖包?
在现代前端开发中,**重复的第三方依赖包(Duplicate Dependencies)**是导致项目体积膨胀、加载速度变慢、构建时间延长的常见问题。尤其在使用模块打包工具(如 Webpack、Vite、Rollup)时,若项目或其依赖的库…...

Java开发中复用公共SQL的方法
在一次Java后端开发的面试中,面试官问了我一个问题:“你在写代码时会复用公共SQL吗?如果会的话,能详细介绍一下你是如何实现的吗?”这个问题让我眼前一亮,因为在实际项目中,SQL复用确实是一个非…...

【西门子杯工业嵌入式-2-点亮一颗LED】
西门子杯工业嵌入式-2-点亮一颗LED 一、课程回顾与目标1.上节课内容回顾2.本节课目标 二、硬件连接与原理1. 硬件连接方式2. 连接实例 三、GPIO原理知识1. GPIO结构2. 推挽输出模式原理 四、软件实现步骤1. 项目结构设置2. 函数定义3. led.c 文件编写初始化函数 led_init交替闪…...

代码随想录算法训练营第60期第五十五天打卡
大家好,我们今天继续我们图论的部分,其实我们昨天是主要讲解了深搜与广搜的理论基础,我们大体上了解了两种算法的差异与适用情景,今天我们就继续我们的图论的章节,以后几天的题目是图论中比较有名的问题叫做岛屿问题&a…...

重磅更新! 基于Gemini 2.5 Pro打造的AI智能体PlantUML-X上线!
目录 图表绘制AI智能体PlantUML-X上线通过简单的提示词创建各种UML图:轻松搞定其它类型的技术图表: AI智能体PlantUML-X功能实测画一个在Java中的一个简单的用户登录功能的时序图效果展示:根据详细内容生成系统架构图效果展示:效果…...

[5-02-04].第01节:Jmeter环境搭建:
JMeter笔记大纲 Jmeter依赖于JDK,所以必须确保当前计算机上已经安装了JDK,并且配置了环境变量 一、JMeter概述: 1.1.JMeter是什么: JMeter是Appache组织使用java开发的一款测试工具 可以用于对服务器、网络或对象模拟巨大的负载…...
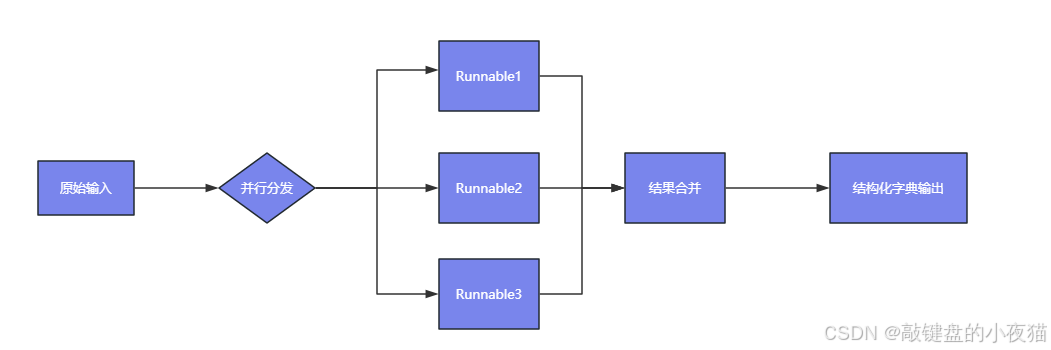
AI智能推荐实战之RunnableParallel并行链
导读:在现代AI应用开发中,如何高效处理多维度数据分析始终是开发者面临的核心挑战。当您需要同时进行情感分析、关键词提取和实体识别,或者要对比多个AI模型的输出结果时,传统的串行处理方式往往效率低下。 本文将深入解析LangCha…...

windows server2019 不成功的部署docker经历
由于现场网络限制,需要将docker 容器部署到windows-server 2019上 1.在windows server 2019上安装 docker-desktop,貌似内核版本太低,无法安装,g 然后曲线救国,window server 2019安装docker,折腾了半天,貌…...

Gemini开源项目DeepResearch:基于LangGraph的智能研究代理技术原理与实现
引言 在人工智能快速发展的今天,如何构建一个能够进行深度研究、自主学习和迭代优化的AI系统成为了技术前沿的重要课题。Gemini开源的DeepResearch一周收获7.9k Star,Google的开源项目Gemini DeepResearch技术通过结合LangGraph框架和Gemini大语言模型&…...

React状态管理Context API + useReducer
在 React 中,Context API useReducer 是一种轻量级的状态管理方案,适合中小型应用或需要跨组件共享复杂状态的场景。它避免了 Redux 的繁琐配置,同时提供了清晰的状态更新逻辑。 1. 基本使用步骤 (1) 定义 Reducer 类似于 Redux 的 reduce…...

【无标题】路径着色问题的革命性重构:拓扑色动力学模型下的超越与升华
路径着色问题的革命性重构:拓扑色动力学模型下的超越与升华 一、以色列路径着色模型的根本局限 mermaid graph TB A[以色列路径着色模型] --> B[强连通约束] A --> C[仅实边三角剖分] A --> D[静态色彩分配] B --> E[无法描述非相邻关系] C --> F[忽…...

Doris Catalog 联邦分析查询性能优化:从排查到优化的完整指南
在大数据分析中,Doris 的 Catalog 联邦分析功能为整合多源数据提供了有力支持。然而,在实际应用中,可能会遇到各种问题影响其正常运行。本文将详细剖析这些问题并提供解决方案。 一、联邦分析查询慢:内外表通用排查逻辑 当遇到 …...

01 Deep learning神经网络的编程基础 二分类--吴恩达
二分类 1. 核心定义 二分类任务是监督学习中最基础的问题类型,其目标是将样本划分为两个互斥类别。设样本特征空间为 X ⊆ R n \mathcal{X} \subseteq \mathbb{R}^n X⊆Rn,输出空间为 Y { 0 , 1 } \mathcal{Y} \{0,1\} Y{0,1},学习目标为…...

视频自动化分割方案:支持按时间与段数拆分
在日常视频处理任务中,如何快速将一个较长的视频文件按照指定规则拆分为多个片段,是许多用户都会遇到的问题。尤其对于需要批量处理视频的开发者、自媒体运营者或内容创作者来说,手动剪辑不仅效率低下,还容易出错。这是一款绿色免…...

Open SSL 3.0相关知识以及源码流程分析
Open SSL 3.0相关知识以及源码流程分析 编译 windows环境编译1、工具安装 安装安装perl脚本解释器、安装nasm汇编器(添加到环境变量)、Visual Studio编译工具 安装dmake ppm install dmake # 需要过墙2、开始编译 # 1、找到Visual Studio命令行编译工具目录 或者菜单栏直接…...

股指期货合约价值怎么算?
股指期货合约价值就是你买一手股指期货合约,理论上值多少钱。这个价值是根据期货的价格和合约乘数来计算的。就好比你买了一斤苹果,价格是5块钱一斤,那你买一斤就得付5块钱。股指期货也是一样,只不过它的计算稍微复杂一点点。 一…...

【QT】使用QT帮助手册找控件样式
选择帮助—》输入stylesheet(小写)—》选择stylesheet—》右侧选择Qt Style Sheets Reference 2.使用CtrlF—》输入要搜索的控件—》点击Customizing QScrollBar 3.显示参考样式表–》即可放入QT-designer的样式表中...

计算机网络(5)——数据链路层
1.概述 数据链路层负责一套链路上从一个节点向另一个物理链路直接相连的相邻节点传输数据报。换言之,主要解决相邻节点间的可靠数据传输 节点(nodes):路由器和主机 链路(links):连接相邻节点的通信信道 2.数据链路层服务 2.1 组帧 组帧(fra…...

VuePress完美整合Toast消息提示
VuePress 整合 Vue-Toastification 插件笔记 记录如何在 VuePress 项目中整合使用 vue-toastification 插件,实现优雅的消息提示。 一、安装依赖 npm install vue-toastification或者使用 yarn: yarn add vue-toastification二、配置 VuePress 客户端增…...

JVM 调优参数详解与实践
JVM 是 Java 程序性能的关键,合理的调优可以显著提升系统稳定性和吞吐量。本文将从基础参数出发,结合线上生产实践,对常用调优参数进行深入剖析与实战分享。 一、JVM内存结构概览 在进行JVM参数调优前,了解JVM内存结构非常关键 堆内存(Heap):用于存储对象,是GC主要处理…...

adb 连不上真机设备问题汇总
问题一、无法弹出 adb 调试授权弹窗 详细描述: 开发者选项中已打开 usb 调试,仅充电模式下 usb 调试也已打开,电脑通过 usb 连上手机后,一直弹出 adb 调试授权弹窗,尝试取消授权再次连接,还是无法弹出问题…...
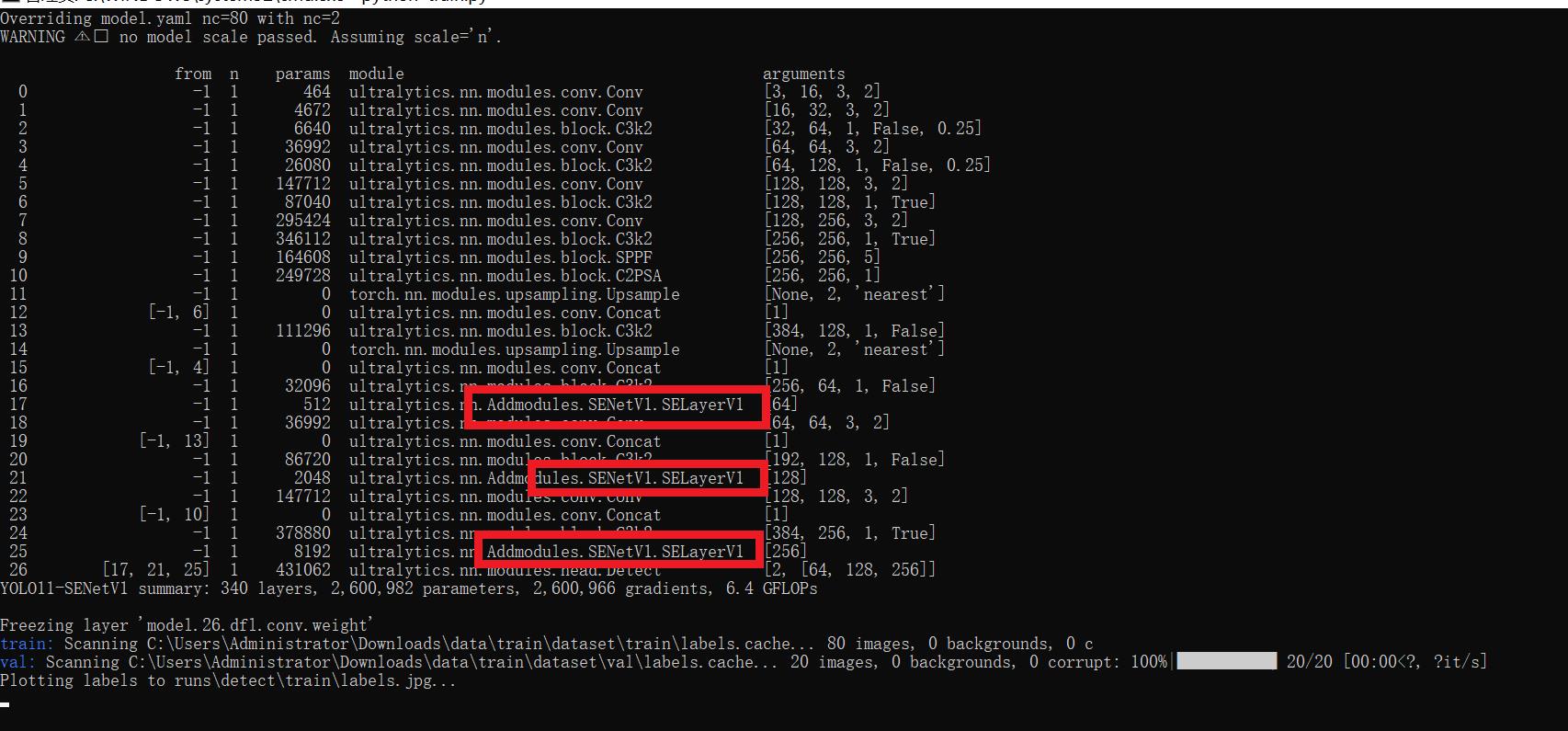
[yolov11改进系列]基于yolov11引入注意力机制SENetV1或者SENetV2的python源码+训练源码
本文给大家带来的改进机制是SENet(Squeeze-and-Excitation Networks)其是一种通过调整卷积网络中的通道关系来提升性能的网络结构。SENet并不是一个独立的网络模型Q,而是一个可以和现有的任何一个模型相结合的模块(可以看作是一种…...

鸿蒙仓颉语言开发实战教程:商城搜索页
大家好,今天要分享的是仓颉语言商城应用的搜索页。 搜索页的内容比较多,都有点密集恐惧症了,不过我们可以从上至下将它拆分开来,逐一击破。 导航栏 搜索页的的最顶部是导航栏,由返回按钮和搜索框两部分组成,比较简单…...

上门服务小程序会员系统框架设计
逻辑分析 会员注册与登录:用户需要能够通过小程序进行会员注册,提供必要信息如手机号码、密码等,注册成功后可登录系统。会员信息管理:包括会员基本信息(姓名、联系方式等)的修改、查看,同时可能…...
