每日算法刷题Day23 6.5:leetcode二分答案3道题,用时1h40min(有点慢)
8. 3007.价值和小于等于K的最大数字(中等,学习,太难,先过)
3007. 价值和小于等于 K 的最大数字 - 力扣(LeetCode)
思想
1.给你一个整数 k 和一个整数 x 。整数 num 的价值是它的二进制表示中在 x,2x,3x 等位置处 设置位 的数目(从最低有效位开始)。num 的 累加价值 是从 1 到 num 的数字的 总 价值。如果 num 的累加价值小于或等于 k 则被认为是 廉价 的。
请你返回 最大 的廉价数字。
2.单调性检验:廉价数字越大,累加价值越容易超过k,所以存在一个最大廉价数字,若此时廉价数字符合条件,小于它的廉价数字也一定符合条件
3.我的想法是可以用二分,但是对于每个mid还要单独再算一遍累加价值会很慢,而如果储存在数组里面也会很耗空间,所以采用遍历res自增写,会超时
4.学习:
(1)数位dp,先不考虑
(2)数学公式
(3)试填法(逐位构造)
代码
c++:
1.我的代码
class Solution {
public:long long cal(long long val, int x) {long long cnt = 0; // 位数long long res = 0;while (val) {++cnt;if (cnt % x == 0 && val & 1) {++res;}val = val >> 1;}return res;}long long findMaximumNumber(long long k, int x) {long long res = 1;long long sum = 0;while (sum + cal(res, x) <= k) {sum += cal(res, x);++res;}return res - 1;}
};
9. LCP 78.城墙防线(中等)
LCP 78. 城墙防线 - 力扣(LeetCode)
思想
1.在探险营地间,小扣意外发现了一片城墙遗迹,在探索期间,却不巧遇到迁徙中的兽群向他迎面冲来。情急之下小扣吹响了他的苍蓝笛,随着笛声响起,遗迹中的城墙逐渐发生了横向膨胀。 已知 rampart[i] = [x,y] 表示第 i 段城墙的初始所在区间。当城墙发生膨胀时,将遵循以下规则:
- 所有的城墙会同时膨胀相等的长度;
- 每个城墙可以向左、向右或向两个方向膨胀。
小扣为了确保自身的安全,需要在所有城墙均无重叠的情况下,让城墙尽可能的膨胀。请返回城墙可以膨胀的 最大值 。
注意: - 初始情况下,所有城墙均不重叠,且
rampart中的元素升序排列; - 两侧的城墙可以向外无限膨胀。
2.单调性检验:膨胀值越大,越不容易满足条件,所以存在一个最大膨胀值,而一旦一个膨胀值满足条件,比它小的值一定可以膨胀,符合单调性
3.我的思想就是贪心,记录前一个城墙用了右侧多少个城墙,从而得出下一个城墙还剩多少个,然后向右拓展尽可能满足条件达到mid,直到循环结束或者有一个城墙没的用了
代码
c++:
class Solution {
public:bool check(vector<vector<int>>& rampart, int mid) {int n = rampart.size();vector<int> cnt(n, 0);int t = 0; // 前一个城墙用了多少for (int i = 1; i < n - 1; ++i) { //[1,n-2]int left = rampart[i][0] - rampart[i - 1][1] - t;if (left >= mid) {t = 0;continue;}int right = rampart[i + 1][0] - rampart[i][1];if (left + right < mid)return false;else {t = mid - left;}}return true;}int rampartDefensiveLine(vector<vector<int>>& rampart) {int res = 0;int left = 0, right = 1e9;while (left <= right) {int mid = left + ((right - left) >> 1);if (check(rampart, mid)) {res = mid;left = mid + 1;} elseright = mid - 1;}return res;}
};
2.3 二分间接值
二分的不是答案,而是一个和答案有关的值(间接值)。
1.套路
c++:
2.题目描述
1.给你一个二维数组 points 和一个字符串 s ,其中 points[i] 表示第 i 个点的坐标,s[i] 表示第 i 个点的 标签 。
如果一个正方形的中心在 (0, 0) ,所有边都平行于坐标轴,且正方形内 不 存在标签相同的两个点,那么我们称这个正方形是 合法 的。
请你返回 合法正方形(条件) 中可以包含的 最多点数(答案,但是二分正方形边长)。
注意:
- 如果一个点位于正方形的边上或者在边以内,则认为该点位于正方形内。
- 正方形的边长可以为零。
2.你有一些球的库存inventory,里面包含着不同颜色的球。一个顾客想要 任意颜色 总数为orders的球。
这位顾客有一种特殊的方式衡量球的价值:每个球的价值是目前剩下的 同色球 的数目。比方说还剩下6个黄球,那么顾客买第一个黄球的时候该黄球的价值为6。这笔交易以后,只剩下5个黄球了,所以下一个黄球的价值为5(也就是球的价值随着顾客购买同色球是递减的)
给你整数数组inventory,其中inventory[i]表示第i种颜色球一开始的数目。同时给你整数orders,表示顾客总共想买的球数目。你可以按照 任意顺序 卖球。
请你返回**卖了orders个球(条件)**以后 最大 总价值之和(答案,但是二分最终球的最大价值)。由于答案可能会很大,请你返回答案对109 + 7取余数 的结果。
3.学习经验
(1)所求答案不好二分,因为不好在check函数中使用,可以间接地二分另一个值,与答案有一定函数关系,最终常数时间求解即可(思考是在二分过程中求解还是二分结束后求解)
(2)可以是一个阈值
1. 3143.正方形中的最多点数(中等)
3143. 正方形中的最多点数 - 力扣(LeetCode)
思想
1.给你一个二维数组 points 和一个字符串 s ,其中 points[i] 表示第 i 个点的坐标,s[i] 表示第 i 个点的 标签 。
如果一个正方形的中心在 (0, 0) ,所有边都平行于坐标轴,且正方形内 不 存在标签相同的两个点,那么我们称这个正方形是 合法 的。
请你返回 合法 正方形中可以包含的 最多 点数。
注意:
- 如果一个点位于正方形的边上或者在边以内,则认为该点位于正方形内。
- 正方形的边长可以为零。
2.单调性检验:正方形边长越大,点数越多,越不容易合法,所以存在一个最大正方形边长,而一旦这个正方形边长满足条件,更小的也一定满足条件,符合单调性
3.用哈希表记录标签即可
4.答案是最多点数,但是二分最多点数不好判断,要计算距离,所以二分正方形边长然后在check里面更新点数res即可
代码
c++:
class Solution {
public:bool check(vector<vector<int>>& points, string s, int mid, int& res) {int n = points.size();unordered_map<char, int> mp;for (int i = 0; i < n; ++i) {int x = points[i][0], y = points[i][1];if (abs(x) <= mid && abs(y) <= mid) {++mp[s[i]];if (mp[s[i]] > 1)return false;}}res = max(res, (int)mp.size());return true;}int maxPointsInsideSquare(vector<vector<int>>& points, string s) {int n = points.size();int res = 0;int maxval = INT_MAX;for (const auto x : points) {maxval = max({maxval, abs(x[0]), abs(x[1])});}long long left = 0, right = maxval;while (left <= right) {long long mid = left + ((right - left) >> 1);if (check(points, s, mid, res)) {left = mid + 1;} elseright = mid - 1;}return res;}
};
2. 1648.销售价值减少的颜色球(中等,重点学习思想)
1648. 销售价值减少的颜色球 - 力扣(LeetCode)
思想
1.你有一些球的库存 inventory ,里面包含着不同颜色的球。一个顾客想要 任意颜色 总数为 orders 的球。
这位顾客有一种特殊的方式衡量球的价值:每个球的价值是目前剩下的 同色球 的数目。比方说还剩下 6 个黄球,那么顾客买第一个黄球的时候该黄球的价值为 6 。这笔交易以后,只剩下 5 个黄球了,所以下一个黄球的价值为 5 (也就是球的价值随着顾客购买同色球是递减的)
给你整数数组 inventory ,其中 inventory[i] 表示第 i 种颜色球一开始的数目。同时给你整数 orders ,表示顾客总共想买的球数目。你可以按照 任意顺序 卖球。
请你返回卖了 orders 个球以后 最大 总价值之和。由于答案可能会很大,请你返回答案对 109 + 7 取余数 的结果。
2.这道题二分查找的是卖了orders个球后总的球的最大价值,即一个阈值k,即
- 所有数量>x的球一定会减小到x,用等差数列求和求价值
- orders仍有剩余,剩余的一定以价值x卖出(因为是个阈值)
而这个阈值越小,卖的球越多,越不容易满足条件,所以存在一个最小值,而一旦这个阈值满足条件,大于它的值一定满足条件
3.二分得到阈值k,答案在二分结束后单独求,而不是在二分里面求解
代码
c++:
class Solution {
public:bool check(vector<int>& inventory, int orders, int mid) {int cnt = 0;for (const int x : inventory) {if (x > mid) {cnt += x - mid;if (cnt > orders)return false;}}return true;}int maxProfit(vector<int>& inventory, int orders) {long long mod = 1e9 + 7;int n = inventory.size();int maxval = INT_MIN;for (const int x : inventory)maxval = max(maxval, x);int left = 0, right = maxval;int k = 0;while (left <= right) {int mid = left + ((right - left) >> 1);if (check(inventory, orders, mid)) {right = mid - 1; // 找更小的k = mid;} elseleft = mid + 1;}// 找到阈值求解reslong long res = 0, sum = 0;for (const int x : inventory) {if (x > k) {// x,卖x-k个,到k+1res = (res + 1LL * (x + k + 1) * (x - k) / 2) % mod;sum += x - k;}}// 剩余的if (sum < orders)res = (res + 1LL * (orders - sum) * k) % mod;return res;}
};
相关文章:
)
每日算法刷题Day23 6.5:leetcode二分答案3道题,用时1h40min(有点慢)
8. 3007.价值和小于等于K的最大数字(中等,学习,太难,先过) 3007. 价值和小于等于 K 的最大数字 - 力扣(LeetCode) 思想 1.给你一个整数 k 和一个整数 x 。整数 num 的价值是它的二进制表示中在 x,2x,3x …...

【Android基础回顾】七:内存管理机制
Android 的内存管理机制是一个多层次的复杂系统,旨在高效利用有限的物理内存(RAM),在保证前台应用流畅运行的同时,尽可能在后台保留更多应用以提高启动速度(多任务)。 它的核心机制结合了 Linu…...

数据结构哈希表总结
349. 两个数组的交集 力扣题目链接(opens new window) 题意:给定两个数组,编写一个函数来计算它们的交集。 说明: 输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序。 public int[] intersection(int[] nums1, int[] num…...

Spring事务失效-----十大常见场景及解决方案全解析
Spring事务失效的常见场景及原因分析 Spring事务管理是开发中的核心功能,但在实际应用中可能因各种原因导致事务失效。以下是常见的事务失效场景及详细解析: 1. 方法未被Spring管理 场景:使用new关键字直接创建对象,而非通过Spring容器注入原因:Spring事务基于AOP代理,…...

KMP 算法中 next 数组的构建函数 get_next
KMP 算法中 next 数组的构建函数 get_next ,负责计算模式串的 next 数组,核心是通过递推找到每个位置的 “最长相等前缀后缀长度”。(下标从 1 开始): 一、函数作用 get_next(SString T, int next[]) 的任务…...

IDEA 开发PHP配置调试插件XDebug
1、安装PHP环境 为了方便,使用的PhpStudy。 安装路径:D:\resources\phpstudy_pro\Extensions\php\php7.3.4nts 2、下载Xdebug Xdebug: Downloads 选择对应的版本下载,本次使用的是7.3。 3、配置Xdebug 在php.ini中添加Xdebug配置。 D…...

奇异值分解(SVD):线性代数在AI大模型中的核心工具
🧑 博主简介:CSDN博客专家、CSDN平台优质创作者,高级开发工程师,数学专业,10年以上C/C, C#, Java等多种编程语言开发经验,拥有高级工程师证书;擅长C/C、C#等开发语言,熟悉Java常用开…...
)
矩阵分解相关知识点总结(二)
文章目录 三、矩阵的QR分解3.1、Givens矩阵与Givens变换3.2、Householder矩阵与Householder变换3.3、QR分解 书接上文矩阵分解相关知识点总结(一) 三、矩阵的QR分解 3.1、Givens矩阵与Givens变换 设非零列向量 x ∈ R n \bm{x}\in {\bf{R}}^n x∈Rn及单…...

MySQL——视图 用户管理 语言访问
目录 视图 用户管理 数据库权限 访问 准备工作 使用函数 mysql界面级工具 连接池 视图 这里的视图与事务中的读视图是两个不同的概念:视图是一个虚拟表,其内容由查询定义。同真实的表一样,视图包含一系列带有名称的列和行数据。视图的…...

二、Sqoop 详细安装部署教程
作者:IvanCodes 日期:2025年6月2日 专栏:Sqoop教程 Apache Sqoop 是一个强大的工具,用于在 Hadoop (HDFS, Hive, HBase) 与关系型数据库 (如 MySQL, PostgreSQL, Oracle) 之间高效传输数据。本教程将详细指导您如何根据官方网站截…...

用Python开启游戏开发之旅
在当今丰富多彩的数字娱乐世界中,游戏以其独特的魅力吸引着无数人的目光。而Python这门功能强大又简洁易懂的编程语言,也为游戏开发打开了一扇充满创意的大门。 一、选择Python的理由 Python之所以备受游戏开发者青睐,有诸多原因。其一&#…...

React 第五十四节 Router中useRevalidator的使用详解及案例分析
前言 useRevalidator 是 React Router v6.4 引入的一个强大钩子,用于在数据路由(Data Router)中手动触发路由数据的重新验证(revalidation)。 它在需要主动刷新数据而不改变路由位置的场景中非常有用。 一、useReval…...

【C语言预处理详解(下)】--#和##运算符,命名约定,命令行定义 ,#undef,条件编译,头文件的包含,嵌套文件包含,其他预处理指令
目录 五.#和##运算符 5.1--#运算符 5.2--##运算符 六.命名约定,#undef,命令行定义 6.1--命名约定 6.2--#undef 6.3--命名行定义 七.条件编译 常见的条件编译指令: 1.普通的条件编译: 2.多个分支的条件编译(可以利用条…...

03.搭建K8S集群
K8S集群搭建的方式 目前主流的搭建k8s集群的方式有kubeadm、minikube、二进制包三种方式: kubeadm(本案例搭建方式) 是一个工具,用于快速搭建kubernetes集群,目前应该是比较方便和推荐的,简单易用 kubea…...

RDMA简介3之四种子协议对比
RDMA协议共有四种子协议,分别为InfiniBand、iWARP、RoCE v1和RoCE v2协议。这四种协议使用统一的RDMA API,但在具体的网络层级实现上有所不同,如图1所示,接下来将分别介绍这四种子协议。 图1 RDMA四种子协议网络层级关系图 Infin…...
【最新版】西陆洗车系统源码全开源+uniapp前端+搭建教程
一.系统介绍 一款基于ThinkPHPUniapp开发的多门店洗车系统,包含用户端(小程序)、门店员工端(小程序)、门店端(PC)、平台管理端(PC)。 门店分连锁门店和独立门店…...

力扣LeetBook数组和字符串--二维数组
1.旋转矩阵 题目链接 想了那么久的各种旋转,对角线,其实把问题搞复杂了。 旋转90度的本质无非就是转置镜像对称 转置是什么?:将矩阵的行和列互换。 镜像对称:把矩阵从中间对折,互换位置 矩阵 A A [ 1 3 0…...

Linux开发工具(apt,vim,gcc)
目录 yum/apt包管理器 Linux编辑器 vim 1.见一见vim 2.vim的多模式 3.命令模式底行模式等 4.vim的配置 Linux编译器 gcc/g 1.预处理(宏替换) 2.编译(生成汇编) 3.汇编(生成机器可识别代码) 4.连…...

C# ExcelWorksheet 贴图
C# ExcelWorksheet 贴图 在C#中,如果你想在Excel工作表中插入图片(例如,在ExcelWorksheet中贴图),你可以使用ClosedXML或EPPlus这样的库来操作Excel文件。下面我将分别介绍如何使用这两个库来实现这一功能。 使用ClosedXML 首先,确保你已经安装了ClosedXML包。你可以通…...

鸿蒙Next开发真机调试签名申请流程
背景: 在学习鸿蒙next开发应用的初期总是会遇到一堆的问题,毕竟鸿蒙next开发不管是他的ArKTS语言还是他的开发工具DevEco Studio都还在起步阶段,就像当初的Android起步一样,总会有资料不足的一些问题。就比如我们学习下载完DevEco…...
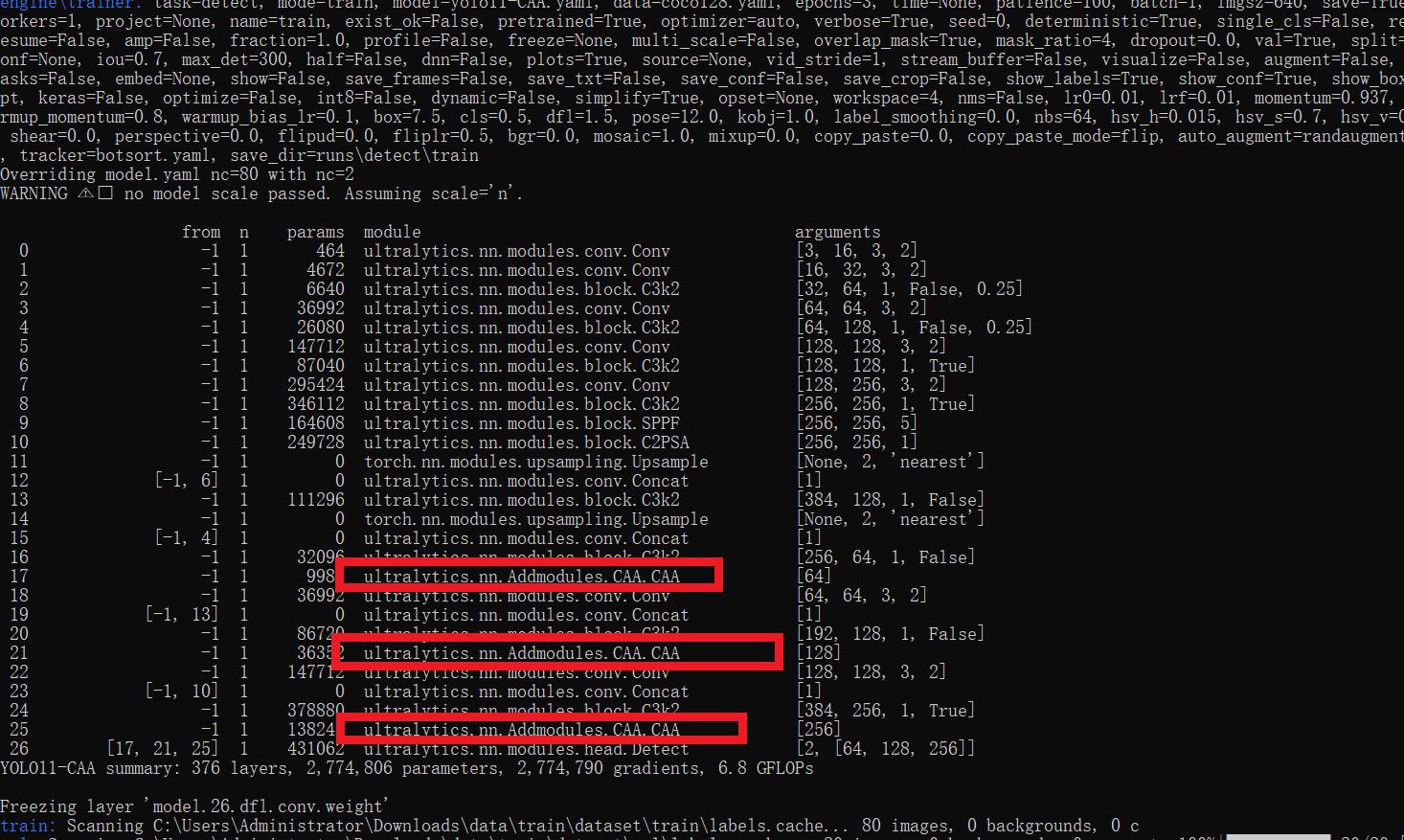
[yolov11改进系列]基于yolov11引入上下文锚点注意力CAA的python源码+训练源码
【CAA介绍】 本文记录的是基于CAA注意力模块的RT-DETR目标检测改进方法研究。在远程遥感图像或其他大尺度变化的图像中目标检测任务中,为准确提取其长距离上下文信息,需要解决大目标尺度变化和多样上下文信息时的不足的问题。CAA能够有效捕捉长距离依赖…...

【Elasticsearch】 查询优化方式
在优化Elasticsearch的查询性能时,可以从多个维度着手,包括索引设计、查询优化、集群配置、数据管理以及监控分析等。常见的优化方式和策略有以下几种: 一、索引优化 合理设计字段类型: 字段类型选择: 对于不需要分词的…...

Xcode 16.4 + iOS 18 系统运行时崩溃:___cxa_current_primary_exception 符号丢失的原因与解决方案
在使用 Xcode 16.4 构建项目,运行到 iOS 18.3 或更早版本系统(包括模拟器)时,出现了如下的运行时崩溃: dyld[22183]: Symbol not found: ___cxa_current_primary_exceptionReferenced from: /.../WidgetOn.app/Widget…...

【linux】全志Tina预编译一个so库文件到根文件系统/usr/lib/下
一、sdk中新建文件夹 路径: V:\t113\work3\t113\openwrt\package\feeds\libs\md5util md5util为需要注入的库文件夹。 文件结构 libs md5util files libmd5util.so makefile etc.. 二、编写makefile include $(TOPDIR)/rules.mkPKG_NAME : md5util PKG_VERSIO…...

C# 类和继承(成员访回修饰符)
成员访回修饰符 本章之前的两节阐述了类的可访问性。对类的可访问性,只有两种修饰符:internal和public。 本节阐述成员的可访问性。类的可访问性描述了类的可见性;成员的可访问性描述了类成员的可 见性。 声明在类中的每个成员对系统的不同…...

c++ stl容器之map用法
目录 (1)map介绍 (2)map、multimap、unordered_map区别 (3)map用法 1.map接口表 2.使用举例 插入数据与遍历数据 查找关键字和值 删除元素 按照值排序 (4)multimap用法 &…...

Linux-文件管理及归档压缩
1.根下的目录作用说明: /:Linux系统中所有的文件都在根下/bin:(二进制命令目录)存放常用的用户命令/boot:系统启动时的引导文件(内核的引导配置文件,grub配置文件,内核配置文件) 例…...

结合Jenkins、Docker和Kubernetes等主流工具,部署Spring Boot自动化实战指南
基于最佳实践的Spring Boot自动化部署实战指南,结合Jenkins、Docker和Kubernetes等主流工具,提供从环境搭建到生产部署的完整流程: 一、环境准备与工具选型 1.基础设施 Jenkins服务器:安装Jenkins LTS版本,配置JDK(推荐JDK 11+)及Maven/Gradle插…...

微软认证考试科目众多?该如何选择?
在云计算、人工智能、数据分析等技术快速发展的今天,微软认证(Microsoft Certification)已成为IT从业者、开发者、数据分析师提升竞争力的重要凭证。但面对众多考试科目,很多人不知道如何选择。本文将详细介绍微软认证的考试方向、…...

MCP协议在LLM系统中的架构与实现原理研究
MCP协议的角色和功能定位 模型上下文协议(Model Context Protocol, MCP) 是由Anthropic公司(Claude模型的发布方)提出的一种开放协议,旨在标准化大型语言模型(LLM)与外部数据源、工具和服务之间的交互方式。可以将MCP类比为AI应用的“USB-C接口”:通过统一的接口协议,…...
