[蓝桥杯]搭积木
搭积木
题目描述
小明对搭积木非常感兴趣。他的积木都是同样大小的正立方体。
在搭积木时,小明选取 mm 块积木作为地基,将他们在桌子上一字排开,中间不留空隙,并称其为第 0 层。
随后,小明可以在上面摆放第 1 层,第 2 层,......,最多摆放至第 nn 层。摆放积木必须遵循三条规则:
规则 1:每块积木必须紧挨着放置在某一块积木的正上方,与其下一层的积木对齐;
规则 2:同一层中的积木必须连续摆放,中间不能留有空隙;
规则 3:小明不喜欢的位置不能放置积木。
其中,小明不喜欢的位置都被标在了图纸上。图纸共有 nn 行,从下至上的每一行分别对应积木的第 1 层至第 nn 层。每一行都有 mm 个字符,字符可能是 '.' 或 'X' ,其中 'X' 表示这个位置是小明不喜欢的。
现在,小明想要知道,共有多少种放置积木的方案。他找到了参加蓝桥杯的你来帮他计算这个答案。
由于这个答案可能很大,你只需要回答这个答案对 109+7109+7 取模后的结果。
注意:地基上什么都不放,也算作是方案之一种。
输入描述
输入格式:
输入数据的第一行有两个正整数 n,m (n≤100,m≤100)n,m (n≤100,m≤100),表示图纸的大小。
随后 nn 行,每行有 mm 个字符,用来描述图纸。每个字符只可能是 '.' 或 'X' 。
输出描述
输出一个整数,表示答案对 109+7109+7 取模后的结果。
输入输出样例
示例
输入
2 3
..X
.X.
输出
4
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
总通过次数: 296 | 总提交次数: 490 | 通过率: 60.4%
难度: 困难 标签: 2018, 国赛, 动态规划, 搜索
算法思路:动态规划 + 二维前缀和优化
本题需要计算在给定限制条件下搭建积木的方案数,核心是区间覆盖的动态规划,通过二维前缀和优化状态转移。以下是详细思路:
关键规则分析
- 地基规则:地基(第0层)固定,方案数包含“什么都不放”的情况
- 连续规则:每层积木必须连续且对齐
- 禁止规则:'X'位置不能放置积木
- 层级关系:第i层的积木必须完全包含在第i-1层的积木范围内
动态规划定义
- 状态设计:
dp[i][l][r]表示在第i层(图纸层)放置区间[l, r]积木的方案数(1 ≤ i ≤ n, 1 ≤ l ≤ r ≤ m) - 状态转移:
dp[i][l][r] = Σ dp[i+1][x][y]其中 x ≤ l, y ≥ r(第i+1层区间必须覆盖当前层) - 前缀和优化:用二维前缀和
sum[x][y]加速区间和计算
算法步骤
- 初始化:
- 第n层:合法区间方案数为1
- 总方案数
ans初始为1(什么都不放)
- 自顶向下DP:
- 从第n层向下到第1层
- 计算第i+1层的前缀和
- 根据覆盖规则计算第i层方案数
- 累加方案:
- 每层合法区间方案累加入
ans
- 每层合法区间方案累加入
- 输出结果:
ans % 1e9+7
状态转移图解
第i+1层:覆盖区间[x,y]|-----------| ← y| [l,r] |x→ |-----------|↑必须满足:x ≤ l 且 y ≥ r第i层:区间[l,r](需被完全覆盖)代码实现(C++)
#include <iostream>
#include <vector>
using namespace std;const int mod = 1000000007;int main() {int n, m;cin >> n >> m;vector<string> grid(n);for (int i = 0; i < n; i++) {cin >> grid[i];}// dp[i][l][r]: 第i层放置区间[l,r]的方案数vector<vector<vector<int>>> dp(n + 1, vector<vector<int>>(m + 1, vector<int>(m + 1, 0)));long long ans = 1; // 包含"什么都不放"的情况// 初始化第n层for (int l = 1; l <= m; l++) {for (int r = l; r <= m; r++) {bool valid = true;for (int j = l - 1; j <= r - 1; j++) {if (grid[n - 1][j] == 'X') {valid = false;break;}}if (valid) {dp[n][l][r] = 1;ans = (ans + 1) % mod;}}}// 自顶向下DP(从n-1层到1层)for (int i = n - 1; i >= 1; i--) {// 计算第i+1层的前缀和vector<vector<int>> sum(m + 1, vector<int>(m + 1, 0));for (int x = 1; x <= m; x++) {for (int y = 1; y <= m; y++) {long long val = dp[i + 1][x][y];val = (val + sum[x - 1][y]) % mod;val = (val + sum[x][y - 1]) % mod;val = (val - sum[x - 1][y - 1] + mod) % mod;sum[x][y] = val;}}// 计算第i层DP值for (int l = 1; l <= m; l++) {for (int r = l; r <= m; r++) {// 检查禁止位置bool valid = true;for (int j = l - 1; j <= r - 1; j++) {if (grid[i - 1][j] == 'X') {valid = false;break;}}if (!valid) {dp[i][l][r] = 0;continue;}// 状态转移:Σ(x≤l, y≥r) dp[i+1][x][y]long long temp = sum[l][m]; // x≤l, y≤mtemp = (temp - sum[l][r - 1] + mod) % mod; // 减去y<r的部分dp[i][l][r] = temp;ans = (ans + temp) % mod;}}}cout << ans << endl;return 0;
}实例验证(输入样例)
输入:2 3..X.X.
输出:4计算过程:
- 第2层(顶层):
[1,1]:合法 →dp[2][1][1]=1[3,3]:合法 →dp[2][3][3]=1- 其他区间非法 → 方案数0
- 累计:
ans=1+2=3
- 第1层:
[1,1]:合法,覆盖dp[2][1][1]→ 方案数1- 其他区间非法 → 方案数0
- 累计:
ans=3+1=4
注意事项
- 下标处理:
- 图纸行索引:
grid[i-1]对应第i层 - 字符索引:区间
[l, r]对应字符串[l-1, r-1]
- 图纸行索引:
- 负数取模:
- 减法后加
mod再取模,避免负数
- 减法后加
- 空间优化:
- 三维数组大小:
(n+1)×(m+1)×(m+1) - 最大空间:
101×101×101×4B ≈ 4MB
- 三维数组大小:
- 时间优化:
- 二维前缀和将转移复杂度从O(m⁴)降至O(m²)
- 总复杂度:O(n×m²)
优化建议
- 滚动数组:用
dp[2][m][m]替代三维数组 - 区间压缩:连续'.'区间合并减少状态数
- 剪枝策略:
- 提前终止全'X'层的计算
- 跳过无效区间(l>r)
相关文章:

[蓝桥杯]搭积木
搭积木 题目描述 小明对搭积木非常感兴趣。他的积木都是同样大小的正立方体。 在搭积木时,小明选取 mm 块积木作为地基,将他们在桌子上一字排开,中间不留空隙,并称其为第 0 层。 随后,小明可以在上面摆放第 1 层&a…...

在MATLAB中使用自定义的ROS2消息
简明结论: 无论ROS2节点和MATLAB运行在哪,MATLAB本机都必须拥有自定义消息源码并本地用ros2genmsg生成,才能在Simulink里订阅这些消息。只要你想让MATLAB或Simulink能识别自定义消息,必须把消息包源码(.msg等)拷到本机指定目录&a…...

使用C/C++和OpenCV实现图像拼接
使用 C 和 OpenCV 实现图像拼接 本文将详细介绍如何利用 OpenCV 库,在 C 环境中实现图像拼接。图像拼接技术可以将多张具有重叠区域的图像合成为一张高分辨率的全景图。OpenCV 提供了一个功能强大的 Stitcher 类,它封装了从特征点检测、匹配到图像融合的…...

神经网络-Day46
目录 一、 什么是注意力二、 特征图的提取2.1 简单CNN的训练2.2 特征图可视化 三、通道注意力3.1 通道注意力的定义3.2 模型的重新定义(通道注意力的插入) 一、 什么是注意力 注意力机制,本质从onehot-elmo-selfattention-encoder-bert这就是…...

Ubuntu中常用的网络命令指南
Ubuntu中常用的网络命令指南 在Ubuntu系统中,网络管理是日常运维和故障排查的核心技能。 🛠️ 基础网络诊断 ping - 测试网络连通性 ping google.com # 持续测试 ping -c 4 google.com # 发送4个包后停止traceroute / tracepath - 追踪数据包路径 …...

JVM——如何打造一个类加载器?
引入 在Java应用程序的生命周期中,类加载器扮演着至关重要的角色。它是Java运行时环境的核心组件之一,负责在需要时动态加载类文件到JVM中。理解类加载器的工作原理以及如何自定义类加载器,不仅可以帮助我们更好地管理应用程序的类加载过程&…...

【MATLAB去噪算法】基于ICEEMDAN联合小波阈值去噪算法
ICEEMDAN联合小波阈值去噪算法相关文献 (注:目前相关论文较少,应用该套代码可发直接一些水刊) 一、CEEMDAN的局限性 模式残留噪声问题:原始CEEMDAN在计算每个IMF时直接对噪声扰动的信号进行模态分解并平均。 后果&a…...

c++ Base58编码解码
Base58 字符集 Base58 使用 58 个字符进行编码,字符集为:123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz。注意:0(零)、O(大写字母O)、I(大写字母I)和 l&a…...

证券交易柜台系统解析与LinkCounter解决方案开发实践
第一章 证券交易柜台系统基础解析 1.1 定义与行业定位 证券交易柜台系统(Trading Counter System)是券商经纪业务的核心支撑平台,承担投资者指令传输、风险控制、清算结算等职能。根据中国证监会《证券期货业网络信息安全管理办法》要求&am…...

XXTEA,XTEA与TEA
TEA、XTEA和XXTEA都是分组加密算法,它们在设计、安全性、性能等方面存在显著区别。以下是它们的主要区别: 密钥长度 TEA:使用128位密钥。 XTEA:通常使用128位或256位密钥。 XXTEA:密钥长度更灵活,可以使用任…...

机器人玩转之---嵌入式开发板基础知识到实战选型指南(包含ORIN、RDK X5、Raspberry pi、RK系列等)
1. 基础知识讲解 1.1 什么是嵌入式开发板? 嵌入式开发板是一种专门设计用于嵌入式系统开发的硬件平台,它集成了微处理器、内存、存储、输入输出接口等核心组件于单块印刷电路板上。与传统的PC不同,嵌入式开发板具有体积小、功耗低、成本适中…...

腾讯云国际版和国内版账户通用吗?一样吗?为什么?
在当今全球化的数字化时代,云计算服务成为众多企业和个人拓展业务、存储数据的重要选择。腾讯云作为国内领先的云服务提供商,其国际版和国内版备受关注。那么,腾讯云国际版和国内版账户是否通用?它们究竟一样吗?背后又…...

OrCAD X Capture CIS设计小诀窍系列第二季--03.如何在Capture中输出带有目录和元器件信息的PDF
背景介绍:我们在进行原理图设计时,经常需要输出PDF来查看或评审,但通过”Print”功能导出的PDF较为简单,只能查看设计视图;而通过使用Ghostscript软件可以输出带有目录和元器件信息的PDF,让设计师可以直接在…...

汽车的安全性能测试:试验台铁地板的重要性
汽车的安全性能测试是非常重要的,其中试验台铁地板的设计和材料选择起着至关重要的作用。试验台铁地板是指在进行汽车碰撞、侧翻等试验时,用于支撑汽车底部和提供稳定支撑的重要部件。 在进行汽车碰撞试验时,试验台铁地板的设计和材料需要具…...

Lua和JS的垃圾回收机制
Lua 和 JavaScript 都采用了 自动垃圾回收机制(GC) 来管理内存,开发者无需手动释放内存,但它们的 实现机制和行为策略不同。下面我们从原理、策略、优缺点等方面来详细对比: 🔶 1. 基本原理对比 特性LuaJa…...

实践指南:从零开始搭建RAG驱动的智能问答系统
LLM 赋能的最强大的应用之一是复杂的问答 (Q&A) 聊天机器人。这些是可以回答关于特定来源信息问题的应用程序。这些应用程序使用一种称为检索增强生成的技术,或 RAG。本文将展示如何基于 LangChain 构建一个简单的基于非结构化数据文本数据源的问答应用程序。 温…...

边缘计算服务器
边缘计算服务器的核心要点解析,综合技术架构、应用场景与部署方案: 一、核心定义与技术特性 本质定位 部署在网络边缘侧的专用计算设备(如工厂车间、智慧路灯等),直接处理终端设备(传感器、摄像头等…...

矩阵的偏导数
设 X ( x i j ) m n X (x_{ij})_{m \times n} X(xij)mn,函数 f ( X ) f ( x 11 , x 12 , … , x 1 n , x 21 , … , x m n ) f(X) f(x_{11}, x_{12}, \ldots, x_{1n}, x_{21}, \ldots, x_{mn}) f(X)f(x11,x12,…,x1n,x21,…,xmn) 是一个 m n…...

第R9周:阿尔茨海默病诊断(优化特征选择版)
文章目录 1. 导入数据2. 数据处理2.1 患病占比2.2 相关性分析2.3 年龄与患病探究 3. 特征选择4. 构建数据集4.1 数据集划分与标准化4.2 构建加载 5. 构建模型6. 模型训练6.1 构建训练函数6.2 构建测试函数6.3 设置超参数 7. 模型训练8. 模型评估8.1 结果图 8.2 混淆矩阵9. 总结…...

电动螺丝刀-多实体拆图建模案例
多实体建模要注意下面两点: 多实体建模的合并结果一定要谨慎在实际工作中多实体建模是一个非常好的思路,先做产品的整体设计,再将个体零件导出去做局部细节设计 电动螺丝刀模型动图展示 爆炸视图动图展示 案例素材点击此处获取 建模步骤 1. …...

当丰收季遇上超导磁测量:粮食产业的科技新征程
麦浪藏光阴,心田种丰年!又到了一年中最令人心潮澎湃的粮食丰收季。金色的麦浪随风翻滚,沉甸甸的稻穗谦逊地低垂着,处处洋溢着丰收的喜悦。粮食产业,无疑是国家发展的根基与命脉,是民生稳定的压舱石。在现代…...

电子电气架构 --- 什么是功能架构?
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

Android四大组件通讯指南:Kotlin版组件茶话会
某日,Android王国举办Kotlin主题派对。Activity穿着Jetpack Compose定制礼服,Service戴着协程手表,BroadcastReceiver拿着Flow喇叭,ContentProvider抱着Room数据库入场。它们正愁如何交流,Intent举着"邮差"牌…...
材质(Materials))
C++.OpenGL (11/64)材质(Materials)
材质(Materials) 真实感材质系统 #mermaid-svg-NjBjrmlcpHupHCFQ {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-NjBjrmlcpHupHCFQ .error-icon{fill:#552222;}#mermaid-svg-NjBjrmlcpHupHCFQ .error-text{fill:…...

AudioRelay 0.27.5 手机充当电脑音响
—————【下 载 地 址】——————— 【本章下载一】:https://pan.xunlei.com/s/VOS4MvfPxrnfS2Zu_YS4egykA1?pwdi2we# 【本章下载二】:https://pan.xunlei.com/s/VOS4MvfPxrnfS2Zu_YS4egykA1?pwdi2we# 【百款黑科技】:https://uc…...

会计 - 合并1- 业务、控制、合并日
一、业务 1.1 业务的定义以及构成要素 业务,是指企业内部某些生产经营活动或资产的组合,该组合一般具有投入、加工处理过程和产出能力,能够独立计算其成本费用或所产生的收入。 (1)投入,指原材料、人工、必要的生产技术等无形资产以及构成产出能力的机器设备等其他长期资…...

前端项目eslint配置选项详细解析
文章目录 1. 前言2、错误级别3、常用规则4、目前项目使用的.eslintrc.js 1. 前言 ESLint 是一个可配置的 JavaScript 代码检查工具,旨在帮助开发者发现并修复代码中的潜在问题,包括语法错误、逻辑错误以及风格不一致等问题。以下是其核心功能和特点…...

NVIDIA Dynamo:数据中心规模的分布式推理服务框架深度解析
NVIDIA Dynamo:数据中心规模的分布式推理服务框架深度解析 摘要 NVIDIA Dynamo是一个革命性的高吞吐量、低延迟推理框架,专为在多节点分布式环境中服务生成式AI和推理模型而设计。本文将深入分析Dynamo的架构设计、核心特性、代码实现以及实际应用示例&…...

第十三节:第四部分:集合框架:HashMap、LinkedHashMap、TreeMap
Map集合体系 HashMap集合的底层原理 HashMap集合底层是基于哈希表实现的 LinkedHashMap集合的底层原理 TreeMap集合的底层原理 代码: Student类 package com.itheima.day26_Map_impl;import java.util.Objects;public class Student implements Comparable<Stu…...
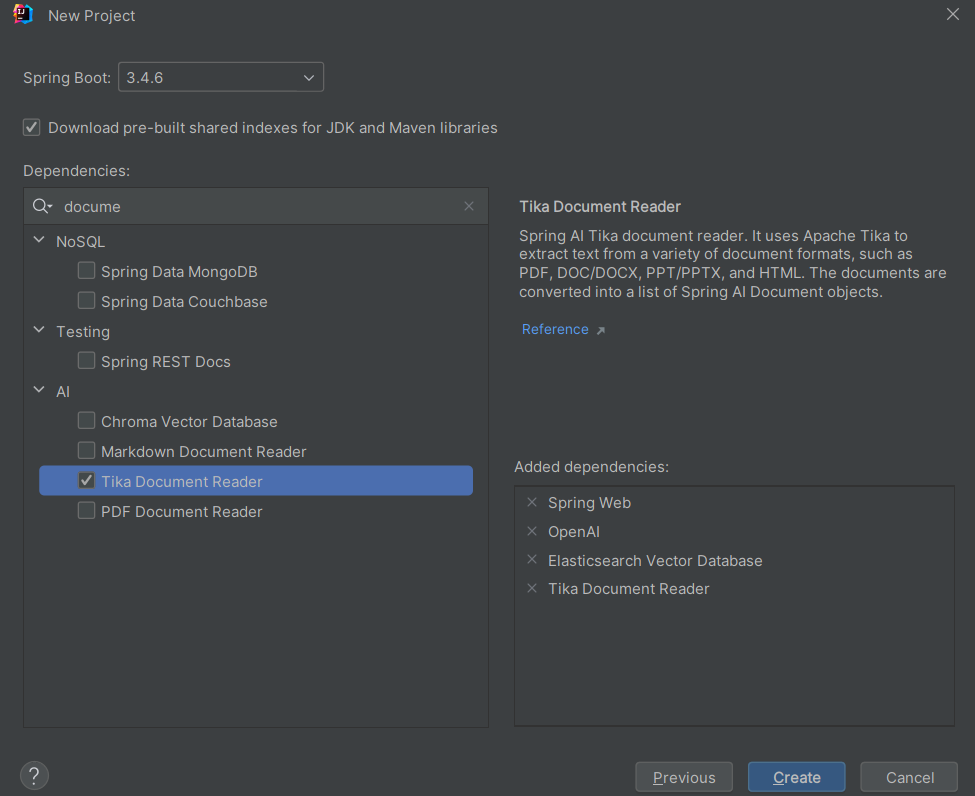
Spring AI之RAG入门
目录 1. 什么是RAG 2. RAG典型应用场景 3. RAG核心流程 3.1. 检索阶段 3.2. 生成阶段 4. 使用Spring AI实现RAG 4.1. 创建项目 4.2. 配置application.yml 4.3. 安装ElasticSearch和Kibana 4.3.1. 安装并启动ElasticSearch 4.3.2. 验证ElasticSearch是否启动成功 …...
