N元语言模型 —— 一文讲懂!!!
目录
引言
一. 基本知识
二.参数估计
三.数据平滑
一.加1法
二.减值法/折扣法
编辑 1.Good-Turing 估计
编辑 2.Back-off (后备/后退)方法
3.绝对减值法
编辑4.线性减值法
5.比较
三.删除插值法(Deleted interpolation)
四.模型自适应
引言

本章节讲的知识主要是来解决以上这个问题:即如何计算一段话在我们日常生活中出现的概率。在学完本章节后,你可以尝试解决下面的问题:

一. 基本知识
对于一段话,我们如何计算其在生活中出现的概率呢?首先我们可以把每一句话拆分成一个个词,这些词就是我们所说的“统计基元”,一个个统计基元组成了我们的一句话。而对于我们每一个统计基元来说,其前面的基元就是历史基元。
如何计算一段话的概率?
假设我们这段话是“我爱你”,我们该怎么计算呢?你可能会想到,“我爱你”这句话的概率,不就应该等于“我”出现的概率*“爱”出现的概率*“你”出现的概率。实际上来说,这样算的话我们就忽略了词与词的关系,比如“爱”会不会影响“你”出现的概率,比如我们大部分人都会把“爱你”连起来说,这样的话我们就不能把他们俩独立开来了。这样的话,就相当于我们计算概率的时候要参考一句话前面的基元。因此我们应该用下面的公式:

可以理解为:句子的概率 = 第 1 个词的概率 × 第 2 个词依赖第 1 个词的概率 × 第 3 个词依赖前两个词的概率 × … × 第 m 个词依赖前 m - 1 个词的概率
历史基元数量爆炸问题
显然随着要预测的词位置越靠后(i 越大 ),需要参考的 “历史基元数量” 也越多(i−1 个 ),这样的话很容易出现后面的历史基元越来越多出现参数爆炸。即:

那我们该如何解决这个问题呢?
我们的解决办法是等价类划分:


举个例子:“我爱你”和“石头爱地”这两句话,假设n等于2,则“你”前面的“我爱”和“地”前面的“石头爱”,因为前n-1个基元,即“爱” 相同,则这俩句话为同一等价类。因此我们很容易看出来,这个n其实就是相当于缩减了我们的视野,我们只看前n-1个基元而看不到更前面的基元了。
因此:

但是,这样的话,显然我们的句子的第一个单词没有前置的选项让我们看了,也就是说没有历史基元,这对我们是非常不方便的,因为我们无法统一编程,并且我们还丢失了其作为第一个单词的位置信息。所以我们为这个句子加上了开头和结尾符号来标识。
即:
这样的话我们就非常好求解了,例题如下:

(下面三个分别是一元,二元,三元划分) 那么我们的概率就是:


二.参数估计
好了,既然我们已经整出来了表示,那么我们模型里的这些参数是啥呢?就是说我们这里的P是什么呢?这就引出了我们下面的概念:



例题:


那若是求一个句子里包含从没出现的词呢?这是很常见的,比如训练语料不可能包含所有人的姓名,如果一个人的姓名比较生僻,比如叫“诸葛大力”,这样的话是否“诸葛大力爱张伟”在日常生活中是不可能发生的呢?显然不是。但是我们的计算下整个的概率是0。显然是不合理的。于是我们便引出了数据平滑。
三.数据平滑


困惑度你就理解为这个句子的常见程度,如果困惑度很高,说明句子很罕见,让人看着很“困惑”。
一.加1法

意思就是分子加1,分母加上词汇库的总量(不包含开始和结束字符)
例题:

二.减值法/折扣法
 1.Good-Turing 估计
1.Good-Turing 估计


 举例:
举例:

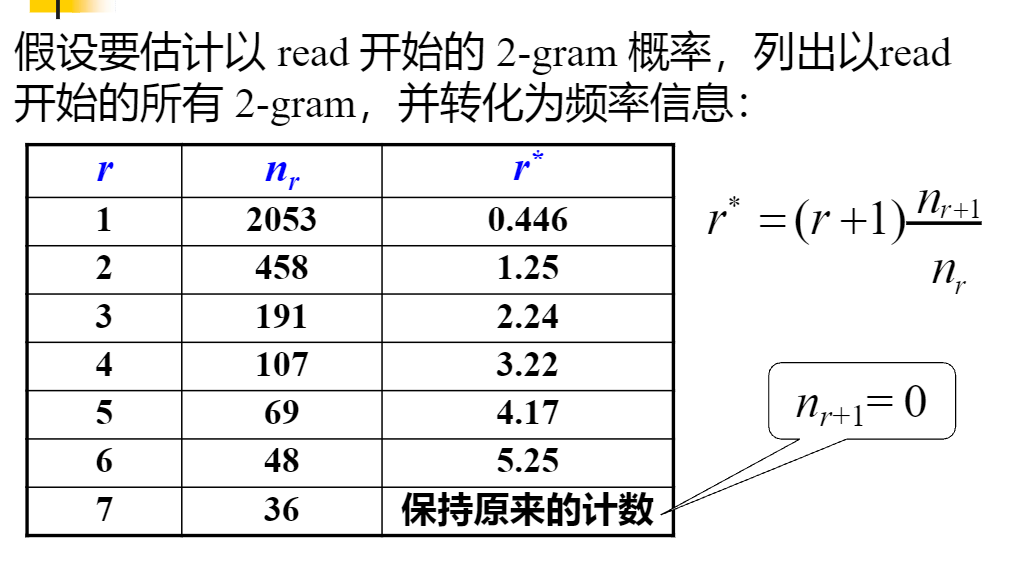 给你们算个一个吧。第一个r*,照着公式的话,r+1等于2,因为我们这里的r等于1,然后nr和nr+1直接看表的话就是2053和458,也就是说r*=2*(458/2053)约等于0.446,其他的你们照着我这样做就行。
给你们算个一个吧。第一个r*,照着公式的话,r+1等于2,因为我们这里的r等于1,然后nr和nr+1直接看表的话就是2053和458,也就是说r*=2*(458/2053)约等于0.446,其他的你们照着我这样做就行。


 2.Back-off (后备/后退)方法
2.Back-off (后备/后退)方法



3.绝对减值法
 4.线性减值法
4.线性减值法

5.比较

三.删除插值法(Deleted interpolation)


四.模型自适应







相关文章:

N元语言模型 —— 一文讲懂!!!
目录 引言 一. 基本知识 二.参数估计 三.数据平滑 一.加1法 二.减值法/折扣法 编辑 1.Good-Turing 估计 编辑 2.Back-off (后备/后退)方法 3.绝对减值法 编辑4.线性减值法 5.比较 三.删除插值法(Deleted interpolation) 四.模型自适应 引言 本章节讲的…...

.NET 9中的异常处理性能提升分析:为什么过去慢,未来快
一、为什么要关注.NET异常处理的性能 随着现代云原生、高并发、分布式场景的大量普及,异常处理(Exception Handling)早已不再只是一个冷僻的代码路径。在高复杂度的微服务、网络服务、异步编程环境下,服务依赖的外部资源往往不可…...

Mac 安装git心路历程(心累版)
省流版:直接安装Xcode命令行工具即可,不用安Xcode。 git下载官网 第一部分 上网初步了解后,打算直接安装Binary installer,下载完安装时,苹果还阻止安装,只好在“设置–安全性与隐私”最下面的提示进行安…...

计算机网络第2章(下):物理层传输介质与核心设备全面解析
目录 一、传输介质1.1 传输介质的分类1.2 导向型传输介质1.2.1 双绞线(Twisted Pair)1.2.2 同轴电缆(Coaxial Cable)1.2.3 光纤(Optical Fiber)1.2.4 以太网对有线传输介质的命名规则 1.3 非导向型传输介质…...

Qt Creator 11.0创建ROS2 Humble工程
Qt Creator 11.0创建ROS2 Humble项目工程 安装ROSProjectManager插件创建ROS2项目在src下添加packagegit clone ROS2功能包编译运行安装ROSProjectManager插件 安装ROSProjectManager的主要流程参考官方的流程,地址(ros_qtc_plugin)。 此处采用二进制安装: sudo apt inst…...

C# 类和继承(扩展方法)
扩展方法 在迄今为止的内容中,你看到的每个方法都和声明它的类关联。扩展方法特性扩展了这个边 界,允许编写的方法和声明它的类之外的类关联。 想知道如何使用这个特性,请看下面的代码。它包含类MyData,该类存储3个double类型 的…...

机器学习复习3--模型的选择
选择合适的机器学习模型是机器学习项目成功的关键一步。这通常不是一个一蹴而就的过程,而是需要综合考虑多个因素,并进行实验和评估。 1. 理解问题本质 这是模型选择的首要步骤。需要清晰地定义试图解决的问题类型: 监督学习 : 数据集包含…...

MySQL复杂SQL(多表联查/子查询)详细讲解
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 MySQL复杂SQL(多表联查/子查询&a…...

STM32使用土壤湿度传感器
1.1 介绍: 土壤湿度传感器是一种传感装置,主要用于检测土壤湿度的大小,并广泛应用于汽车自动刮水系统、智能灯光系统和智能天窗系统等。传感器采用优质FR-04双料,大面积5.0 * 4.0厘米,镀镍处理面。 它具有抗氧化&…...
的标准写法)
在C++中,头文件(.h或.hpp)的标准写法
目录 1.头文件保护(Include Guards)2.包含必要的标准库头文件3.前向声明(Forward Declarations)4.命名空间5.注释示例1:基础头文件示例2:包含模板和内联函数的头文件示例3:C11风格的枚举类头文件…...

Axios学习笔记
Axios简介 axios前端异步请求库类似JQuery ajax技术, ajax用来在页面发起异步请求到后端服务,并将后端服务响应数据渲染到页面上, jquery推荐ajax技术,但vue里面并不推荐在使用jquery框架,vue推荐使用axios异步请求库。…...
:Chain构建与组合技巧)
Langchain学习笔记(十一):Chain构建与组合技巧
注:本文是Langchain框架的学习笔记;不是教程!不是教程!内容可能有所疏漏,欢迎交流指正。后续将持续更新学习笔记,分享我的学习心得和实践经验。 前言 在LangChain的发展过程中,API设计经历了重…...

【判断既约分数】2022-4-3
缘由既约分数,除了辗转相除法-编程语言-CSDN问答 void 判断既约分数() {int a 1, b 2020, aa b, y 2, gs 0;while (aa){while (a < b){while (y < a && y < aa)if (a%y 0 && aa%y 0)a, y 2;elsey;if (a < b)gs; else;a, y 2;…...

Windows平台RTSP/RTMP播放器C#接入详解
大牛直播SDK在Windows平台下的RTSP、RTMP播放器模块,基于自研高性能内核,具备极高的稳定性与行业领先的超低延迟表现。相比传统基于FFmpeg或VLC的播放器实现,SmartPlayer不仅支持RTSP TCP/UDP自动切换、401鉴权、断网重连等网络复杂场景自适应…...

深圳SMT贴片工艺优化关键步骤
内容概要 深圳SMT贴片工艺优化作为现代电子制造的核心环节,聚焦于提升生产精度与稳定性。其技术框架围绕三大核心维度展开:温度动态调控、设备协同适配与工艺缺陷预判。通过精密温度曲线控制系统,实现回流焊环节的热能梯度精准匹配ÿ…...

从 JDK 8 到 JDK 17:Swagger 升级迁移指南
点击上方“程序猿技术大咖”,关注并选择“设为星标” 回复“加群”获取入群讨论资格! 随着 Java 生态向 JDK 17 及 Jakarta EE 的演进,许多项目面临从 JDK 8 升级的挑战,其中 Swagger(API 文档工具)的兼容性…...

配置git命令缩写
以下是 Git 命令缩写的配置方法及常用方案,适用于 Linux/macOS/Windows 系统: 🔧 一、配置方法 1. 命令行设置(推荐) # 基础命令缩写 git config --global alias.st status git config --global alias.co che…...

Redis 缓存问题及其解决方案
1. 缓存雪崩 概念:缓存雪崩是指在缓存层出现大范围缓存失效或缓存服务器宕机的情况下,大量请求直接打到数据库,导致数据库压力骤增,甚至可能引发数据库宕机。 影响:缓存雪崩会导致系统性能急剧下降,甚至导…...

使用 Coze 工作流一键生成抖音书单视频:全流程拆解与技术实现
使用 Coze 工作流一键生成抖音书单视频:全流程拆解与技术实现(提供工作流) 摘要:本文基于一段关于使用 Coze 平台构建抖音爆火书单视频的详细讲解,总结出一套完整的 AI 视频自动化制作流程。内容涵盖从思路拆解、节点配…...

【发布实录】云原生+AI,助力企业全球化业务创新
5 月 22 日,在最新一期阿里云「飞天发布时刻」,阿里云云原生应用平台产品负责人李国强重磅揭晓面向 AI 场景的云原生产品体系升级,通过弹性智能的一体化架构、开箱即用的云原生 AI 能力,为中国企业出海提供新一代技术引擎。 发布会…...

vue中的派发事件与广播事件,及广播事件应用于哪些场景和一个表单验证例子
在 Vue 2.X 中,$dispatch 和 $broadcast 方法已经被废弃。官方认为基于组件树结构的事件流方式难以理解,并且在组件结构扩展时容易变得脆弱。因此,Vue 2.X 推荐使用其他方式来实现组件间的通信,例如通过 $emit 和 $on 方法&#x…...

DeepSeek 赋能智能养老:情感陪伴机器人的温暖革新
目录 一、引言二、智能养老情感陪伴机器人的市场现状与需求2.1 市场现状2.2 老年人情感陪伴需求分析 三、DeepSeek 技术详解3.1 DeepSeek 的技术特点3.2 与其他类似技术的对比优势 四、DeepSeek 在智能养老情感陪伴机器人中的具体应用4.1 自然语言处理与对话交互4.2 情感识别与…...

LabVIEW主轴故障诊断案例
LabVIEW 开发主轴机械状态识别与故障诊断系统,适配工业场景主轴振动监测需求。通过整合品牌硬件与软件算法,实现从信号采集到故障定位的全流程自动化,为设备维护提供数据支撑,提升数控机床运行可靠性。 面向精密制造企业数控机…...

gRPC 的四种通信模式完整示例
gRPC 的四种基本通信模式,包括完整的 .proto 文件定义和 Go 语言实现代码: 1. 简单 RPC (Unary RPC) - 请求/响应模式 客户端发送单个请求,服务端返回单个响应 calculator.proto protobuf syntax "proto3";package calculato…...

C#中Struct与IntPtr转换:实用扩展方法
C#中Struct与IntPtr转换:实用扩展方法 在 C# 编程的世界里,我们常常会遇到需要与非托管代码交互,或者进行一些底层内存操作的场景。这时,IntPtr类型就显得尤为重要,它可以表示一个指针或句柄,用来指向非托…...

Web安全:XSS、CSRF等常见漏洞及防御措施
Web安全:XSS、CSRF等常见漏洞及防御措施 一、XSS(跨站脚本攻击) 定义与原理 XSS攻击指攻击者将恶意脚本(如JavaScript、HTML标签)注入到Web页面中,当用户访问该页面时,脚本在浏览器端执行&…...
)
Java基础之数组(附带Comparator)
文章目录 基础概念可变参数组数组与ListComparator类1,基本概念2,使用Comparator的静态方法(Java 8)3,常用Comparator方法4,例子 排序与查找数组复制其他 基础概念 int[] anArray new int[10];只有创建对象时才会使用new关键字,所以数组是个…...

计算机组成与体系结构:补码数制二(Complementary Number Systems)
目录 4位二进制的减法 补码系统 🧠减基补码 名字解释: 减基补码有什么用? 计算方法 ❓为什么这样就能计算减基补码 💡 原理揭示:按位减法,模拟总减法! 那对于二进制呢?&…...

C#使用MindFusion.Diagramming框架绘制流程图(2):流程图示例
上一节我们初步介绍MindFusion.Diagramming框架 C#使用MindFusion.Diagramming框架绘制流程图(1):基础类型-CSDN博客 这里演示示例程序: 新建Windows窗体应用程序FlowDiagramDemo,将默认的Form1重命名为FormFlowDiagram. 右键FlowDiagramDemo管理NuGet程序包 输入MindFusio…...

【物联网-ModBus-RTU
物联网-ModBus-RTU ■ 优秀博主链接■ ModBus-RTU介绍■(1)帧结构■(2)查询功能码 0x03■(3)修改单个寄存器功能码 0x06■(4)Modbus RTU 串口收发数据分析 ■ 优秀博主链接 Modbus …...
