数论总结,(模版与题解)
数论
- 欧拉函数
- X质数(线性筛与二进制枚举)
- 求解组合数
- 欧拉降幂(乘积幂次)
- 乘法逆元
- 最小质因子之和
- 模版
欧拉函数
欧拉函数的定义就是小于等于n的数里有f(n)个数与n互质,下面是求欧拉函数的模版。

package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.Scanner;public class 欧拉函数模版 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();for (int i = 0; i < n; i++) {int x = scanner.nextInt();System.out.println(oula(x));}}static int oula(int x){int res = x;for (int i = 2; i <= x / i; i++) {if (x % i == 0) {res = res / i * (i - 1);while (x % i == 0) {x /= i;}}}if(x > 1){res = res / x * (x-1);}return res;}
}X质数(线性筛与二进制枚举)
package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.ArrayList;public class X质数 {public static void main(String[] args) {//线性筛把质数筛出来int[] minp = new int[1000001];ArrayList<Integer> prime = new ArrayList<>();boolean[] isp = new boolean[1000001];for (int i = 2; i <= 1000000; i++) {if(minp[i] == 0){prime.add(i);}for (int pp : prime){if(pp * i > 1000000){break;}minp[i * pp] = pp;if(minp[i] == pp){break;}}}for (int pp : prime){isp[pp] = true;}int ans = 0;//二进制遍历判断是否为质数for (int i = 1; i < 1000001; i++) {String s = i + "";int ls = s.length();for (int j = 1; j < Math.pow(2,ls); j++) {String er = Integer.toBinaryString(j);int ler = er.length();String dudu = "";for (int k = ler - 1; k >= 0; k--) {if(er.charAt(k) == '1'){dudu = s.charAt(k + ls -ler) + dudu;}}int now = Integer.parseInt(dudu);if(isp[now]){ans++;break;}}}System.out.println(ans);}
}求解组合数

package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.Scanner;public class 求解组合数 {static int mod = 1000000007;static long[] ni;static long[] jie;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);//求阶乘jie = new long[10000001];jie[0] = 1;for (int i = 1; i < 10000001; i++) {jie[i] = (jie[i-1] * i) % mod;}//求逆元ni = new long[10000001];ni[0] = 1;for (int i = 1; i < 10000001; i++) {ni[i] = niyuan(jie[i]);}int q = scanner.nextInt();for (int i = 0; i < q; i++) {int n = scanner.nextInt();int m = scanner.nextInt();System.out.println((((jie[n] * ni[m]) % mod) * ni[n-m]) % mod);}}//快速乘法幂求逆元static long niyuan(long x){long res = 1;int y = mod - 2;while (y > 0){if((y & 1) == 1){res = (res * x) % mod;}y>>= 1;x = (x * x) % mod;}return res;}
}欧拉降幂(乘积幂次)

package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.Scanner;public class 乘积幂次_欧拉降幂 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int mod = 1000000007;//求幂次long fm = 1;for (int i = 1; i <= m; i++) {fm = (fm * i) % (mod - 1);}//快速乘法幂long en = 1;int x = n;long y = fm;while (y > 0){if((y & 1) == 1){en = (en * x) % mod;}y >>= 1;x = (x * x) % mod;}System.out.println(en);}
}乘法逆元

//package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();int mod = 1000000007;for (int i = 0; i < t; i++) {int n = scanner.nextInt();long x = n;int y = mod - 2;long res = 1;//快速乘法幂while (y > 0){if((y & 1) == 1){res = (res * x) % mod;}y >>= 1;x = (x * x) % mod;}System.out.println(res);}}
}最小质因子之和

模版
package com.js.datastructure.recursion.蓝桥.总结.数论;import java.util.ArrayList;
import java.util.Scanner;public class 最小质因子之和 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int[] minp = new int[20000001];ArrayList<Integer> Prime = new ArrayList<>();for (int i = 2; i < 20000001; i++) {if(minp[i] == 0){Prime.add(i);minp[i] = i;}for (int pp : Prime){if(pp * i > 20000000){break;}minp[pp*i] = pp;if(minp[i] == pp){break;}}}//求前缀和for (int i = 2; i < 20000001; i++) {minp[i] = minp[i-1] + minp[i];}int t = scanner.nextInt();for (int i = 0; i < t; i++) {int n = scanner.nextInt();System.out.println(minp[n]);}}
}package com.js.datastructure.recursion.蓝桥.国特训练营.数论;import java.util.ArrayList;public class 模版 {static ArrayList<Integer> prime;static int[] minp;public static void main(String[] args) {}//快速乘法幂//有取余的时候都取余static long fast(int x, int y){long res = 1;while (y > 0){if((y & 1) == 1){res = res * x;}y>>=1;x = x * x;}return res;}//线性筛static void shai(){for (int i = 2; i < minp.length; i++) {if(minp[i] == 0){prime.add(i);minp[i] = i;}for (int pp : prime){if(pp * i >= minp.length){break;}minp[pp*i] = pp;if(minp[i] == pp){break;}}}}//欧拉函数:就是小于这个数和他互质数的个数,质数为n-1static int oula(int x){int res = x;for (int i = 2; i <= x / i; i++) {if(x % i == 0){res = res / i * (i-1);while (x % i == 0){x/=i;}}}if(x > 1){res = res / x * (x-1);}return res;}//求逆元//模数为质数是,逆元为a^m-2 % m ,用快速乘法幂//大组合数
}相关文章:

数论总结,(模版与题解)
数论 欧拉函数X质数(线性筛与二进制枚举)求解组合数欧拉降幂(乘积幂次)乘法逆元最小质因子之和模版 欧拉函数 欧拉函数的定义就是小于等于n的数里有f(n)个数与n互质,下面是求欧拉函数的模版。 package com.js.datas…...

EasyRTC嵌入式音视频通信SDK助力物联网/视频物联网音视频打造全场景应用
一、方案概述 随着物联网技术的飞速发展,视频物联网在各行业的应用日益广泛。实时音视频通信技术作为视频物联网的核心支撑,其性能直接影响着系统的交互体验和信息传递效率。EasyRTC作为一款成熟的音视频框架,具备低延迟、高画质、跨平台等…...
1-2 Linux-虚拟机(2025.6.7学习篇- win版本)
1、虚拟机 学习Linux系统,就需要有一个可用的Linux系统。 如何获得?将自己的电脑重装系统为Linux? NoNo。这不现实,因为Linux系统并不适合日常办公使用。 我们需要借助虚拟机来获得可用的Linux系统环境进行学习。 借助虚拟化技术&…...

Deepseek基座:Deepseek-v2核心内容解析
DeepSeek原创文章1 DeepSeek-v3:基于MLA的高效kv缓存压缩与位置编码优化技术 2 Deepseek基座:DeepSeek LLM核心内容解析 3 Deepseek基座:Deepseek MOE核心内容解析 4 Deepseek基座:Deepseek-v2核心内容解析 5Deepseek基座…...
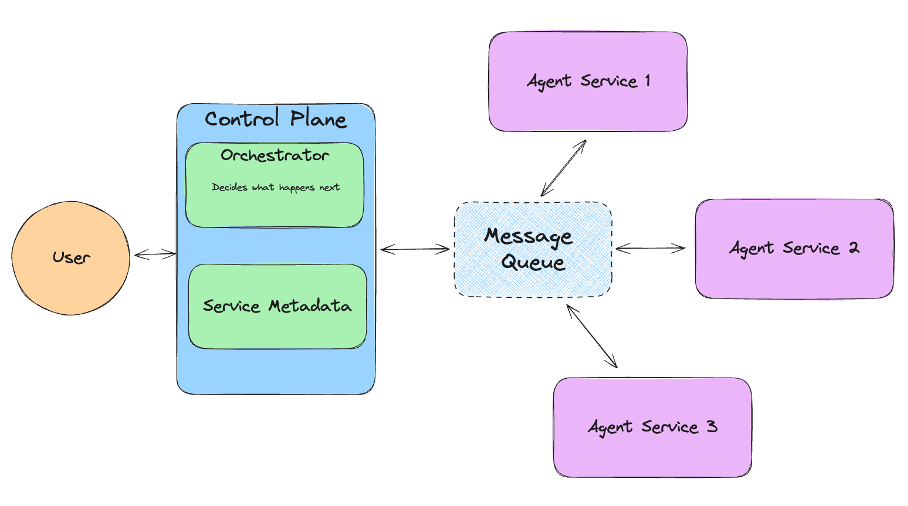
2025主流智能体Agent终极指南:Manus、OpenManus、MetaGPT、AutoGPT与CrewAI深度横评
当你的手机助手突然提醒"明天会议要带投影仪转接头",或是电商客服自动生成售后方案时,背后都是**智能体(Agent)**在悄悄打工。这个AI界的"瑞士军刀"具备三大核心特征: 自主决策能力:像老司机一样根据路况实时…...
家政小程序开发——AI+IoT技术融合,打造“智慧家政”新物种
基于用户历史订单(如“每周一次保洁”)、设备状态(如智能门锁记录的清洁频率),自动生成服务计划。 结合天气数据(如“雨天推荐玻璃清洁”),动态推送服务套餐。 IoT设备联动&#x…...

Keil开发STM32生成hex文件/bin文件
生成hex文件生成bin文件 STM32工程的hex文件和bin文件都可以通过Keil直接配置生成 生成hex文件 工程中点击魔术棒,在 Output 中勾选 Create HEX File 选项,OK保存工程配置 编译工程通过后可以看到编译输出窗口有创建hex文件的提示 默认可以在Output文…...

Windows 系统安装 Redis 详细教程
Windows 系统安装 Redis 详细教程 一、Redis 简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的高性能键值存储系统,常被用作数据库、缓存和消息中间件。相比传统数据库,Redis 具有以下优势: 超高性能…...
)
“组件、路由懒加载”,在 Vue3 和 React 中分别如何实现? (copy)
Vue3 和 React 组件懒加载实现方式 React 中组件懒加载的实现方式 React 提供了 React.lazy 和 Suspense 两个 API 来实现组件的懒加载。React.lazy 用于动态导入组件,而 Suspense 则用于指定加载过程中的占位内容。例如,可以通过以下代码实现懒加载&a…...

.NET 事件模式举例介绍
.NET 事件模式:实现对象间松耦合通信 在软件开发中,对象之间的通信是一个常见且重要的问题。.NET 框架提供了一种标准化的事件模式,用于解决对象间的通信问题,实现松耦合的交互方式。今天,我们就通过一个简单的例子来…...

PDF 转 Markdown
本地可部署的模型 Marker Marker 快速准确地将文档转换为 markdown、JSON 和 HTML。 转换所有语言的 PDF、图像、PPTX、DOCX、XLSX、HTML、EPUB 文件在给定 JSON 架构 (beta) 的情况下进行结构化提取设置表格、表单、方程式、内联数学、链接、引用和代…...

北大开源音频编辑模型PlayDiffusion,可实现音频局部编辑,比传统 AR 模型的效率高出 50 倍!
北大开源了一个音频编辑模型PlayDiffusion,可以实现类似图片修复(inpaint)的局部编辑功能 - 只需修改音频中的特定片段,而无需重新生成整段音频。此外,它还是一个高性能的 TTS 系统,比传统 AR 模型的效率高出 50 倍。 自回归 Tra…...

蒲公英盒子连接问题debug
1、 现象描述 2、问题解决 上图为整体架构图,其中左边一套硬件设备是放在机房,右边是放在办公室。左边的局域网连接了可以访问外网的路由器,利用蒲公英作为旁路路由将局域网暴露在外网环境下。 我需要通过蒲公英作为旁路路由来进行远程访问&…...

Unity | AmplifyShaderEditor插件基础(第五集:简易膨胀shader)
一、👋🏻前言 大家好,我是菌菌巧乐兹~本节内容主要讲一下,如何用shader来膨胀~ 效果预览: 二、💨膨胀的基本原理 之前的移动是所有顶点朝着一个方向走,所以是移动 如果所有顶点照着自己的方…...

Django核心知识点全景解析
引言 本文深入剖析Django核心组件,涵盖数据交换、异步交互、状态管理及安全认证,附完整代码示例和避坑指南! 目录 引言 一、JSON:轻量级数据交换标准 1. 核心特性 2. 标准格式 3. 各语言处理方法 4. 常见错误示例 二、AJA…...

生物发酵展同期举办2025中国合成生物学与生物制造创新发展论坛
一、会议介绍 2025中国合成生物学与生物制造创新发展论坛暨上海国际合成生物学与生物制造展览会于2025年8月7-9日在上海新国际博览中心(浦东新区龙阳路2345号)召开,本次论坛汇聚了国内外顶尖学者、行业领袖及政策制定者,将围绕“…...

WINUI——Magewell视频捕捉开发手记
背景 因需要融合视频,并加载患者CT中提取出的气管镜与病变,以便能实时查看气管镜是否在正确位置。 开发环境 硬件:Magewell的USB Capture HDMI Gen 2 IDE:VS2022 FrameWork: .Net6 WINUI Package: MVVMToolKit NLog Ma…...

Jetpack Compose 中,DisposableEffect、LaunchedEffect 和 sideEffect 区别和用途
在 Jetpack Compose 中,DisposableEffect、LaunchedEffect 和 sideEffect 都是用于处理副作用(Side Effects)的 API,但它们的用途和触发时机不同。以下是它们的核心概念和区别: 1. 副作用(Side Effect&…...

STM32开发,创建线程栈空间大小判断
1. 使用RTOS提供的API函数(以FreeRTOS为例) 函数原型:UBaseType_t uxTaskGetStackHighWaterMark(TaskHandle_t xTask)功能:获取指定任务堆栈中剩余的最小空间(以字为单位,非字节)。使用步骤&am…...

正则表达式检测文件类型是否为视频或图片
// 配置化文件类型检测(集中管理支持的类型) const FILE_TYPE_CONFIG {video: {extensions: [mp4, webm, ogg, quicktime], // 可扩展支持更多格式regex: /^video\/(mp4|webm|ogg|quicktime)$/i // 自动生成正则},image: {extensions: [jpeg, jpg, png,…...

Qwen大语言模型里,<CLS>属于特殊的标记:Classification Token
Qwen大语言模型里,<CLS>属于特殊的标记:Classification Token 目录 Qwen大语言模型里,<CLS>属于特殊的标记:Classification Token功能解析工作机制应用场景举例说明技术要点在自然语言处理(NLP)领域 都是<CLS> + <SEP>吗?一、CLS和SEP的作用与常见用法1. **CLS标…...

TDengine 开发指南——无模式写入
简介 在物联网应用中,为了实现自动化管理、业务分析和设备监控等多种功能,通常需要采集大量的数据项。然而,由于应用逻辑的版本升级和设备自身的硬件调整等原因,数据采集项可能会频繁发生变化。为了应对这种挑战,TDen…...

分布式互斥算法
1. 概述:什么是分布式互斥 假设有两个小孩想玩同一个玩具(临界资源),但玩具只有一个,必须保证一次只有一个人能够玩。当一个小孩在玩时,另一个小孩只能原地等待,直到玩完才能轮到自己。这就是 …...

第34次CCF-CSP认证真题解析(目标300分做法)
第34次CCF-CSP认证 矩阵重塑(其一)AC代码及解析矩阵重塑(其二)AC代码及解析货物调度AC代码及解析 矩阵重塑(其一) 输入输出及样例: AC代码及解析 1.线性化原矩阵 :由于cin的特性我们…...

video-audio-extractor:视频转换为音频
软件介绍 前几天在网上看见有人分享了一个源码,大概就是py调用的ffmpeg来制作的。 这一次我带来源码版(需要py环境才可以运行),开箱即用版本(直接即可运行) 软件特点 软件功能 视频提取音频:…...

rk3588 区分两个相同的usb相机
有时候会插入两个一模一样的usb相机,担心每次启动他们所对应的设备节点 /dev/video* 会变化,所以需要绑定usb口,区分两个相机。把两个相机都插入后,查看usb信息 rootrk3588:/# udevadm info --attribute-walk --name/dev/video0U…...

[概率论基本概念4]什么是无偏估计
关键词:Unbiased Estimation 一、说明 对于无偏和有偏估计,需要了解其叙事背景,是指整体和抽样的关系,也就是说整体的叙事是从理论角度的,而估计器原理是从实践角度说事;为了表明概率理论(不可…...

乐观锁与悲观锁的实现和应用
乐观锁与悲观锁:原理、实现与应用详解 在并发编程和数据库操作中,乐观锁和悲观锁是两种重要的并发控制策略,它们在原理、实现方式和应用场景上存在显著差异。下面我们将通过图文结合的方式,深入探讨这两种锁机制。 一、基本概念 1…...

PL/SQLDeveloper中数值类型字段查询后显示为科学计数法的处理方式
PL/SQLDeveloper中数值类型字段查询后显示为科学计数法的处理方式 文章目录 PL/SQLDeveloper中数值类型字段查询后显示为科学计数法的处理方式1. 查询效果2. 处理方式3. 再次查询 1. 查询效果 2. 处理方式 3. 再次查询...

【vue】Uniapp 打包Android 文件选择上传问题详解~
需求 uniapp兼容android app,pc,h5的文件选择并上传功能。 需要支持拍照和相册选择,以及选择其他类型文件上传~ 实践过程和问题 开始使用uni-file-picker组件 以为很顺利,android模拟器测试…… 忽略了平台兼容性提示~&#…...
