机器学习监督学习实战四:九种回归算法对波士顿房价数据进行回归预测和评估方法可视化
本项目代码在个人github链接:https://github.com/KLWU07/Machine-learning-Project-practice/tree/main
处理流程
- 1.导入波士顿房价数据集并进行预处理。
- 2.使用 GradientBoostingRegressor 模型进行回归分析。
- 3.通过交叉验证评估模型的性能,计算 MAE、MSE、MBE、RMSE 和 R^2 分数。
- 4.使用 matplotlib 绘制训练集和测试集的真实值与预测值的折线图和散点图,直观展示模型的预测效果。
九种回归算法
| 英文名称 (代码调用) | 中文名称 | 说明 |
|---|---|---|
LinearRegression | 线性回归 | 最简单的回归算法,假设目标变量与特征之间存在线性关系。适用于线性可分的数据集。 |
ElasticNet | 弹性网络回归 | 结合了 L1 和 L2 正则化,是 Lasso 和 Ridge 的结合。适用于特征数量较多且存在多重共线性的数据集。 |
Lasso | Lasso 回归 | 使用 L1 正则化,可以进行特征选择,使一些特征的系数为零。适用于特征数量较多且需要稀疏解的数据集。 |
Ridge | 岭回归 | 使用 L2 正则化,可以处理多重共线性问题。适用于特征数量较多且存在多重共线性的数据集。 |
DecisionTreeRegressor | 决策树回归器 | 基于决策树的回归算法,可以处理非线性关系。适用于特征数量较少且数据分布不均匀的数据集。 |
KNeighborsRegressor | K 近邻回归器 | 基于 K 近邻的回归算法,预测目标值是其最近邻点的平均值。适用于数据点分布较为均匀的数据集。 |
SVR | 支持向量回归器 | 基于支持向量机的回归算法,可以处理非线性关系。适用于特征数量较多且数据分布复杂的数据集。 |
GradientBoostingRegressor | 梯度提升回归器 | 基于梯度提升的回归算法,通过组合多个弱学习器来提高预测性能。适用于特征数量较多且数据分布复杂的数据集。 |
ExtraTreesRegressor | 额外树回归器 | 基于随机森林的回归算法,通过组合多个决策树来提高预测性能。适用于特征数量较多且数据分布复杂的数据集。 |
一、数据集介绍
波士顿房价数据集是机器学习领域中经典的回归分析数据集,用于房价预测,监督学习中的回归问题,目标是通过多个特征预测波士顿地区的房屋中位数价格(MEDV)。共 506 条样本(观测值),每条样本对应一个波士顿城镇的统计数据。典型的单变量回归任务,目标是通过 13 个特征预测MEDV。数据集字段(特征)说明如下
| 序号 | 特征名称 | 名称中文 | 说明 |
|---|---|---|---|
| 1 | CRIM | 人均犯罪率 | 城镇每千人犯罪次数 |
| 2 | ZN | 住宅用地比例 | 25,000 平方英尺以上住宅用地比例(规划限制,非住宅用地比例) |
| 3 | INDUS | 非零售商业用地比例 | 城镇非零售商业用地比例(商业活动密度) |
| 4 | CHAS | 查尔斯河虚拟变量 | 1 = 邻近河流,0 = 不邻近 |
| 5 | NOX | 氮氧化物浓度 | ppm,空气质量指标 |
| 6 | RM | 平均房间数 | 每套住宅的平均房间数 |
| 7 | AGE | 房龄较老房屋占比 | 1940 年前建成的自住房屋比例 |
| 8 | DIS | 就业中心加权距离 | 到波士顿 5 个就业中心的加权距离(通勤便利性) |
| 9 | RAD | 辐射状公路可达性指数 | 交通便利程度,指数越高表示越容易到达高速公路 |
| 10 | TAX | 房产税税率 | 每 1 万美元房产的年税额 |
| 11 | PRTATIO | 师生比 | 城镇师生比(教育资源指标) |
| 12 | B | 黑人比例计算值 | 公式:B = 1000(Bk - 0.63)^2,其中Bk为黑人比例 |
| 13 | LSTAT | 低收入人群比例 | %,社会经济地位指标 |
| 14 | MEDV | 房屋中位数价格 | 单位:千美元,目标变量 |
1.各特征分布情况

二、算法评估
尝试了数据标准化没有很大提升。
1.九种回归算法RMSE 和 R^2 比较
图中的蓝色柱子表示 RMSE,红色柱子表示 R^2 分数。通过这个图,可以直观地比较不同模型的性能。

2.训练集和测试集预测值和真实值可视化
梯度提升回归树模型GradientBoostingRegressor和随机搜索最佳参数,均方根误差RMSE为2.725 (0.540),决定系数R2为 0.903 (0.035)。


3.训练集和测试集预测值和真实值散点图

Best parameters: {'learning_rate': 0.12829684257109286, 'max_depth': 5, 'max_features': 'log2', 'min_samples_leaf': 3, 'min_samples_split': 5, 'n_estimators': 122, 'random_state': 42}
Best cross-validation score: -7.715896901281501
MAE: -1.943 (0.285)
MSE: -7.716 (3.060)
MBE: 0.008 (0.223)
RMSE: 2.725 (0.540)
R2: 0.903 (0.035)
4.特征重要性

5.加入主成分分析PCA降维
评估结果不好,不适合使用降维方法。(pca = PCA
n_components=3 # 降维到 3 个主成分
X_pca = pca.fit_transform(X))



Model: GradientBoostingRegressor
MAE: -4.632 (0.564)
MSE: -48.134 (15.559)
MBE: -0.023 (0.886)
RMSE: 6.845 (1.202)
R2: 0.413 (0.152)
6.网格搜索(Grid Search)最佳参数组合



Best parameters: {'learning_rate': 0.1, 'max_depth': 6, 'max_features': 'sqrt', 'n_estimators': 160, 'random_state': 7}
Best cross-validation score: -8.265665640433037
MAE: -1.951 (0.287)
MSE: -8.266 (3.460)
MBE: -0.011 (0.315)
RMSE: 2.813 (0.595)
R2: 0.897 (0.039)
7.随机搜索(Random Search)
在前参数范围基础上寻找更好一点参数。结果在最前面1
三、完整代码
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression, ElasticNet, Lasso, Ridge
from sklearn.tree import DecisionTreeRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.ensemble import GradientBoostingRegressor, ExtraTreesRegressor
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt# 导入数据
filename = 'housing.csv'
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS','RAD', 'TAX', 'PRTATIO', 'B', 'LSTAT', 'MEDV']
data = read_csv(filename, names=names, delim_whitespace=True)# 将数据分为输入数据和输出结果
array = data.values
X = array[:, 0:13] # 输入特征
Y = array[:, 13] # 输出目标变量# 设置交叉验证参数
n_splits = 10
seed = 7
kfold = KFold(n_splits=n_splits, shuffle=True, random_state=seed)# 定义多个回归模型
models = {'LinearRegression': LinearRegression(),'ElasticNet': ElasticNet(),'Lasso': Lasso(),'Ridge': Ridge(),'DecisionTreeRegressor': DecisionTreeRegressor(),'KNeighborsRegressor': KNeighborsRegressor(),'SVR': SVR(),'GradientBoostingRegressor': GradientBoostingRegressor(),'ExtraTreesRegressor': ExtraTreesRegressor()
}# 定义评分标准
scoring = ['neg_mean_absolute_error', 'neg_mean_squared_error', 'r2']# 定义自定义评分函数
def mean_bias_error(y_true, y_pred):return np.mean(y_pred - y_true)def root_mean_squared_error(y_true, y_pred):return np.sqrt(mean_squared_error(y_true, y_pred))# 评估每个模型
model_names = []
rmse_scores = []
r2_scores = []for name, model in models.items():print(f"Model: {name}")# 计算MAEresult_mae = cross_val_score(model, X, Y, cv=kfold, scoring=scoring[0])print('MAE: %.3f (%.3f)' % (result_mae.mean(), result_mae.std()))# 计算MSEresult_mse = cross_val_score(model, X, Y, cv=kfold, scoring=scoring[1])print('MSE: %.3f (%.3f)' % (result_mse.mean(), result_mse.std()))# 计算R^2result_r2 = cross_val_score(model, X, Y, cv=kfold, scoring=scoring[2])print('R2: %.3f (%.3f)' % (result_r2.mean(), result_r2.std()))# 计算MBE和RMSEmbe_scores = []rmse_scores_temp = []for train_index, test_index in kfold.split(X):X_train, X_test = X[train_index], X[test_index]Y_train, Y_test = Y[train_index], Y[test_index]model.fit(X_train, Y_train)Y_pred = model.predict(X_test)mbe_scores.append(mean_bias_error(Y_test, Y_pred))rmse_scores_temp.append(root_mean_squared_error(Y_test, Y_pred))print('MBE: %.3f (%.3f)' % (np.mean(mbe_scores), np.std(mbe_scores)))print('RMSE: %.3f (%.3f)' % (np.mean(rmse_scores_temp), np.std(rmse_scores_temp)))print("-" * 50)# 保存模型名称、RMSE 和 R^2 分数model_names.append(name)rmse_scores.append(np.mean(rmse_scores_temp))r2_scores.append(np.mean(result_r2))# 绘制柱状图
fig, ax1 = plt.subplots(figsize=(12, 8))# 设置柱状图的位置
bar_width = 0.35
index = np.arange(len(model_names))# 绘制 RMSE 柱状图
ax1.bar(index, rmse_scores, bar_width, label='RMSE', color='tab:blue')
ax1.set_xlabel('Model')
ax1.set_ylabel('RMSE', color='tab:blue')
ax1.tick_params(axis='y', labelcolor='tab:blue')# 创建第二个坐标轴
ax2 = ax1.twinx()# 绘制 R^2 柱状图
ax2.bar(index + bar_width, r2_scores, bar_width, label='R^2', color='tab:red')
ax2.set_ylabel('R^2', color='tab:red')
ax2.tick_params(axis='y', labelcolor='tab:red')# 添加标题和标签
ax1.set_title('Comparison of RMSE and R^2 for Different Models')
ax1.set_xticks(index + bar_width / 2)
ax1.set_xticklabels(model_names, rotation=45, ha='right')
ax1.legend(loc='upper left')
ax2.legend(loc='upper right')plt.tight_layout()
plt.show()
相关文章:

机器学习监督学习实战四:九种回归算法对波士顿房价数据进行回归预测和评估方法可视化
本项目代码在个人github链接:https://github.com/KLWU07/Machine-learning-Project-practice/tree/main 处理流程 1.导入波士顿房价数据集并进行预处理。2.使用 GradientBoostingRegressor 模型进行回归分析。3.通过交叉验证评估模型的性能,计算 MAE、…...

1. Web网络基础 - IP地址核心知识解析
深入解析IP地址与ipconfig命令:网络工程师的必备技能 在网络世界中,IP地址是设备通信的基石。本文将全面解析IP地址的核心概念,并通过ipconfig命令实战演示如何获取关键网络配置信息。 一、IP地址核心知识解析 1. IP地址的本质 定义&#x…...

微软重磅发布Magentic UI,交互式AI Agent助手实测!
微软重磅发布Magentic UI,交互式AI Agent助手实测! 何为Magentic UI? Magentic UI 是微软于5.19重磅发布的开源Agent助手,并于24日刚更新了第二个版本0.04版 从官方的介绍来看,目标是打造一款 以人为中心 的智能助手,其底层由多个不同的智能体系统驱动,能够实现网页浏览…...

c# 完成恩尼格玛加密扩展
c# 完成恩尼格玛加密扩展 恩尼格玛扩展为可见字符恩尼格玛的设备原始字符顺序转子的设置反射器的设置连接板的设置 初始数据的设置第一版 C# 代码第二版 C# 代码 总结 恩尼格玛 在之前,我们使用 python 实现了一版恩尼格玛的加密算法,但是这一版&#x…...

华为 “一底双长焦” 专利公布,引领移动影像新变革
6 月 6 日,国家知识产权局公布的一项专利发明申请吸引了众多目光,该专利发明人为华为技术有限公司,名为 “光学镜头、摄像头模组及电子设备” 。从展示的技术图来看,这一光学镜头呈现出独特的 “一底双镜头结构”,其中…...

老年生活照护实训室建设规划:照护质量评估与持续改进实训体系
随着人口老龄化程度的不断加深,老年生活照护需求日益增长,对专业照护人才的培养提出了更高要求。老年生活照护实训室建设方案作为培养高素质照护人才的重要载体,其核心在于构建科学完善的照护质量评估与持续改进实训体系。通过该体系的建设&a…...

【python深度学习】Day 48 PyTorch基本数据类型与操作
知识点: 随机张量的生成:torch.randn函数卷积和池化的计算公式(可以不掌握,模型会自动计算的)pytorch的广播机制:加法和乘法的广播机制 ps:numpy运算也有类似的广播机制,基本一致 作…...

Go深入学习延迟语句
1 延迟语句是什么 编程的时候,经常会需要申请一些资源,比如数据库连接、文件、锁等,这些资源需要再使用后释放掉,否则会造成内存泄露。但是编程人员经常容易忘记释放这些资源,从而造成一些事故。 Go 语言直接在语言层…...

【大模型】【推荐系统】LLM在推荐系统中的应用价值
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点B.4 两大推荐方法 C 模型结构C.1 知识蒸馏(训练过程)C.2 轻量推理(部署过程) D 实验设计E 个人总结 A 论文出处 论文题目:SLMRec:Distilling…...

uni-app学习笔记二十九--数据缓存
uni.setStorageSync(KEY,DATA) 将 data 存储在本地缓存中指定的 key 中,如果有多个key相同,下面的会覆盖掉原上面的该 key 对应的内容,这是一个同步接口。数据可以是字符串,可以是数组。 <script setup>uni.setStorageSyn…...

csharp基础....
int[][] jaggedArray new int[3][]; jaggedArray[0] new int[] { 1, 2 }; jaggedArray[1] new int[] { 3, 4, 5 }; jaggedArray[2] new int[] { 6, 7, 8, 9 }; 嵌套 反转和排序 List<int> list new List<int> { 1, 2, 3, 4, 5 }; list.Reverse(); Cons…...

【C/C++】EBO空基类优化介绍
空对象优化(Empty Base Optimization,简称 EBO)是 C 编译器的一种 优化技术,用于消除空类作为基类时占用的内存空间,从而避免浪费空间、提升结构体或类的存储效率。 1 什么是“空对象”? 一个**空类&#…...

工作邮箱收到钓鱼邮件,点了链接进去无法访问,会有什么问题吗?
没事的,很可能是被安全网关拦截了。最近做勒索实验,有感而发,不要乱点击邮箱中的附件。 最初我们采用钓鱼邮件投递恶意载荷,发现邮件网关把我们的 exe/bat 程序直接拦截了,换成压缩包也一样拦截了,载荷始终…...

基于安卓的线上考试APP源码数据库文档
摘 要 21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,管理工作的重要性已逐渐被人们所认识,科学化的管理,使信息存…...

【数据结构】顺序表和链表详解(下)
前言:上期我们从顺序表开始讲到了单链表的概念,分类,和实现,而这期我们来将相较于单链表没那么常用的双向链表。 文章目录 一、双向链表二,双向链表的实现一,增1,头插2,尾插3&#x…...

【系统架构设计师】绪论-系统架构概述
目录 绪论 系统架构概述 单选题 绪论 系统架构概述 单选题 1、软件方法学是以软件开发方法为研究对象的学科。其中,()是先对最高居次中的问题进行定义、设计、编程和测试,而将其中未解决的问题作为一个子任务放到下一层次中去…...

SQL-事务(2025.6.6-2025.6.7学习篇)
1、简介 事务是一组操作的集合,它是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。 默认MySQL的事务是自动提交的,也就是说࿰…...

OpenCV 图像通道的分离与合并
一、知识点 1、一张彩色图像可以由R、G、B三个通道的灰度图合并而成。 2、void split(InputArray m, OutputArrayOfArrays mv); (1)、将多通道阵列划分为几个单通道阵列。 (2)、参数说明: m: 要分离的多通道阵列。 mv: 输出的vector容器,每个元素都…...
Virtex II 系列FPGA的配置原理
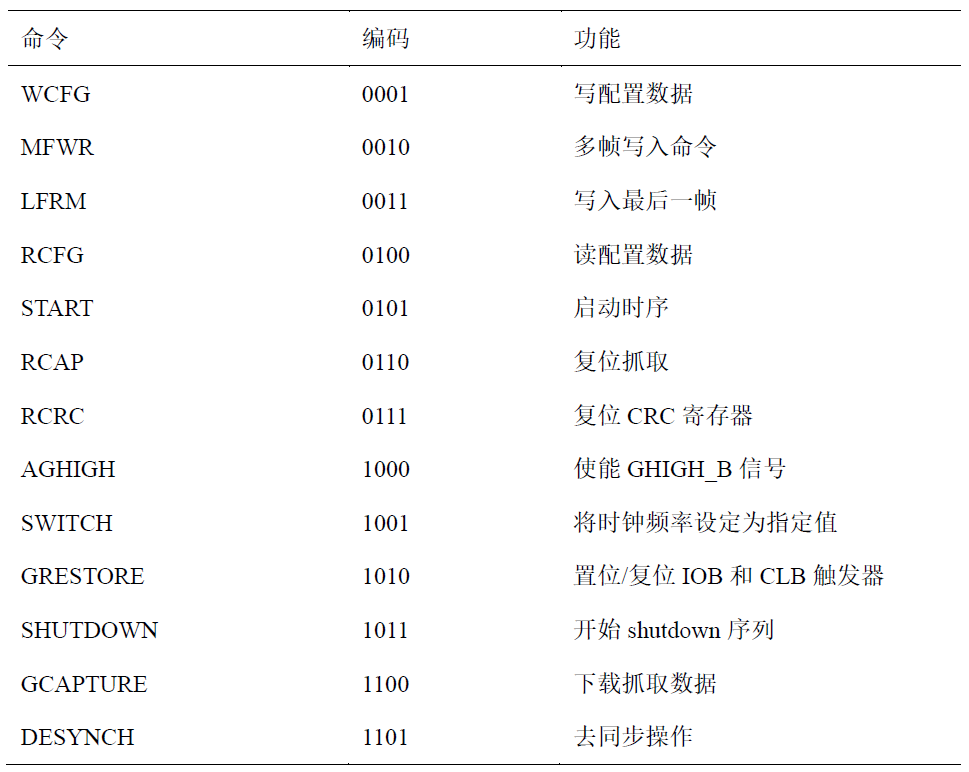
对FPGA 芯片的配置,本质上是将根据设计生成的包含配置命令和配置数据的比特流文件写入到配置存储器中。 1 配置模式 Virtex II 系列FPGA 一共有五种配置模式,配置模式的选择是根据管脚M[2:0]来决定。 (1)串行配置模式 串行配置模…...

蓝桥杯 国赛2024python(b组)题目(1-3)
第一题 试卷答题页 - 蓝桥云课 问题描述 在今年蓝桥杯的决赛中,一共有 1010 道题目,每道题目的分数依次为 55 分,55 分,1010 分,1010 分,1515 分,1515 分,2020 分,2020 分…...

低代码平台前端页面表格字段绑定与后端数据传输交互主要有哪些方式?华为云Astro在这方面有哪些方式?
目录 🔧 一、低代码平台中常见的数据绑定与交互方式 1. 接口绑定(API 调用) 2. 数据源绑定(DataSource) 3. 变量中转(临时变量 / 页面状态) 4. 数据模型绑定(模型驱动) 🌐 二、华为云 Astro 轻应用的实现方式 ✅ 1. 数据源绑定(API服务+API网关) ✅ 2. 变…...

stm32——UART和USART
串口通信协议UART和USART 1. UART与USART协议详解 特性UART (Universal Asynchronous Receiver/Transmitter)USART (Universal Synchronous Asynchronous Receiver/Transmitter)全称通用异步收发器通用同步/异步收发器同步/异步异步:不共享时钟,数据通过…...

算法题(165):汉诺塔问题
审题: 本题需要我们找到最优的汉诺塔搬法然后将移动路径输出 思路: 方法一:递归 我们先分析题目 n为2的情况,我们先将第一个盘子移动到三号柱子上,然后再将二号盘子移动到二号柱子上 n为3的情况,我们先将前…...

玄机——某次行业攻防应急响应(带镜像)
今天给大家带来一次攻防实战演练复现的过程。 文章目录 简介靶机简介1.根据流量包分析首个进行扫描攻击的IP是2.根据流量包分析第二个扫描攻击的IP和漏扫工具,以flag{x.x.x.x&工具名}3.提交频繁爆破密钥的IP及爆破次数,以flag{ip&次数}提交4. 提…...

低代码逻辑引擎配置化实战:三步穿透审批记录查询
在堆积如山的报销单中埋头寻找某笔特殊费用的审批轨迹在跨部门协作时被追问"这个合同到底卡在哪个环节" 在快节奏的办公自动化场景中,这些场景是很常见的,传统OA系统中分散的审批记录查询方式往往太繁琐。 为破解这一痛点,在JVS低…...

深入理解React Hooks的原理与实践
深入理解React Hooks的原理与实践 引言 React Hooks 自 2018 年 React 16.8 发布以来,彻底改变了前端开发者的编码方式。它通过函数式组件提供了状态管理和生命周期等功能,取代了传统的类组件,使得代码更加简洁、复用性更强。然而ÿ…...

WEB3技术重要吗,还是可有可无?
我从几个角度给你一个全面、理性、技术导向的回答: ✅ 一、Web3 技术的重要性:“有意义,但不是万能” Web3 技术并不是可有可无的噱头,而是一种在特定场景下提供独特价值的技术体系。 它重要的原因包括: 1. 重构数字…...

Python 隐藏法宝:双下划线 _ _Dunder_ _
你可能不知道,Python里那些用双下划线包裹的"魔法方法"(Dunder方法),其实是提升代码质量的绝佳工具。但有趣的是,很多经验丰富的开发者对这些方法也只是一知半解。 先说句公道话: 这其实情有可原。因为在多数情况下&am…...

《视觉SLAM十四讲》自用笔记 第三讲:三维空间刚体运动
第三讲 三维空间刚体运动 3.0 目标 1.理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。 2.掌握 Eigen 库的矩阵、几何模块使用方法。 3.1 旋转矩阵 3.1.1 点和向量,坐标系 三维空间中,刚体的运动可以用两个概念来…...

【Zephyr 系列 15】构建企业级 BLE 模块通用框架:驱动 + 事件 + 状态机 + 低功耗全栈设计
🧠关键词:Zephyr、BLE 模块、架构设计、驱动封装、事件机制、状态机、低功耗、可维护框架 📌面向读者:希望将 BLE 项目从“Demo 工程”升级为“企业可复用框架”的研发人员与技术负责人 📊预计字数:5500+ 字 🧭 前言:从 Demo 到产品化,架构该如何升级? 多数 BLE…...
