数据结构基础之排序算法
在数据结构中,常见的排序算法有以下几种:
- 冒泡排序(Bubble Sort):通过比较相邻元素并交换它们的位置,每轮将最大(或最小)的元素冒泡到末尾,重复执行直到排序完成。
function bubbleSort(arr) {const n = arr.length;for (let i = 0; i < n - 1; i++) {for (let j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];}}}return arr;
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(bubbleSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:简单易懂,但对于大型数据集效率较低。
时间复杂度:
最优情况:O(n)(当数组已经排序好时)。
平均情况:O(n^2)。
最坏情况:O(n^2)。
- 插入排序(Insertion Sort):将数组分为已排序和未排序两部分,每次从未排序部分选择一个元素插入到已排序部分的正确位置,重复执行直到排序完成。
function insertionSort(arr) {const n = arr.length;for (let i = 1; i < n; i++) {let key = arr[i];let j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key;}return arr;
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(insertionSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:适用于小型数据集和部分有序数组。
时间复杂度:
最优情况:O(n)(当数组已经排序好时)。
平均情况:O(n^2)。
最坏情况:O(n^2)。
- 选择排序(Selection Sort):每轮从未排序部分选择最小(或最大)的元素,将其与未排序部分的首元素交换,重复执行直到排序完成。
function selectionSort(arr) {const n = arr.length;for (let i = 0; i < n - 1; i++) {let minIdx = i;for (let j = i + 1; j < n; j++) {if (arr[j] < arr[minIdx]) {minIdx = j;}}[arr[i], arr[minIdx]] = [arr[minIdx], arr[i]];}return arr;
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(selectionSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:简单易懂,但对于大型数据集效率较低。
时间复杂度:
最优情况:O(n^2)。
平均情况:O(n^2)。
最坏情况:O(n^2)。
- 快速排序(Quick Sort):通过选取一个基准元素,将数组分成比基准元素小和大的两部分,然后递归地对两部分进行排序。
function quickSort(arr) {if (arr.length <= 1) return arr;const pivot = arr[0];const left = [];const right = [];for (let i = 1; i < arr.length; i++) {if (arr[i] < pivot) {left.push(arr[i]);} else {right.push(arr[i]);}}return [...quickSort(left), pivot, ...quickSort(right)];
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(quickSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:高效且被广泛使用的排序算法。
时间复杂度:
最优情况:O(n log n)。
平均情况:O(n log n)。
最坏情况:O(n^2)。
- 归并排序(Merge Sort):将数组不断分割成较小的子数组,然后再将子数组按顺序合并,重复执行直到排序完成。
function mergeSort(arr) {if (arr.length <= 1) return arr;const mid = Math.floor(arr.length / 2);const left = mergeSort(arr.slice(0, mid));const right = mergeSort(arr.slice(mid));return merge(left, right);
}function merge(left, right) {const mergedArr = [];let leftIdx = 0;let rightIdx = 0;while (leftIdx < left.length && rightIdx < right.length) {if (left[leftIdx] < right[rightIdx]) {mergedArr.push(left[leftIdx]);leftIdx++;} else {mergedArr.push(right[rightIdx]);rightIdx++;}}return [...mergedArr, ...left.slice(leftIdx), ...right.slice(rightIdx)];
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(mergeSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:稳定的排序算法,适用于大型数据集。
时间复杂度:
最优情况:O(n log n)。
平均情况:O(n log n)。
最坏情况:O(n log n)。
- 堆排序(Heap Sort):利用二叉堆(最大堆或最小堆)的特性进行排序,将堆顶元素与最后一个元素交换,然后重建堆,重复执行直到排序完成。
function heapSort(arr) {const n = arr.length;for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {heapify(arr, n, i);}for (let i = n - 1; i >= 0; i--) {[arr[0], arr[i]] = [arr[i], arr[0]];heapify(arr, i, 0);}return arr;
}function heapify(arr, n, i) {let largest = i;const left = 2 * i + 1;const right = 2 * i + 2;if (left < n && arr[left] > arr[largest]) {largest = left;}if (right < n && arr[right] > arr[largest]) {largest = right;}if (largest !== i) {[arr[i], arr[largest]] = [arr[largest], arr[i]];heapify(arr, n, largest);}
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(heapSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:高效的原地排序算法。
时间复杂度:
最优情况:O(n log n)。
平均情况:O(n log n)。
最坏情况:O(n log n)。
- 希尔排序(Shell Sort):是插入排序的一种改进算法,通过分组进行插入排序,逐渐缩小分组间隔,直到分组间隔为1。
function shellSort(arr) {const n = arr.length;for (let gap = Math.floor(n / 2); gap > 0; gap = Math.floor(gap / 2)) {for (let i = gap; i < n; i++) {let temp = arr[i];let j;for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}}return arr;
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(shellSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:插入排序的改进版本,适用于中等大小的数据集。
时间复杂度:
最优情况:O(n log^2 n)(取决于步长序列)。
平均情况:取决于步长序列。
最坏情况:取决于步长序列。
- 计数排序(Counting Sort):适用于一定范围内的整数排序,通过统计每个元素出现的次数,然后计算每个元素的位置,重复执行直到排序完成。
function countingSort(arr) {const n = arr.length;let max = Math.max(...arr);let min = Math.min(...arr);const range = max - min + 1;const count = Array(range).fill(0);const output = Array(n);for (let i = 0; i < n; i++) {count[arr[i] - min]++;}for (let i = 1; i < range; i++) {count[i] += count[i - 1];}for (let i = n - 1; i >= 0; i--) {output[count[arr[i] - min] - 1] = arr[i];count[arr[i] - min]--;}for (let i = 0; i < n; i++) {arr[i] = output[i];}return arr;
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(countingSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:适用于小范围整数排序。
时间复杂度:O(n + k),其中 n 是输入数组元素个数,k 是输入范围大小。
- 桶排序(Bucket Sort):将元素根据一定规则放入不同的桶中,每个桶内部进行排序,然后按顺序合并桶内的元素,重复执行直到排序完成。
function bucketSort(arr, bucketSize = 5) {if (arr.length === 0) return arr;const max = Math.max(...arr);const min = Math.min(...arr);const bucketCount = Math.floor((max - min) / bucketSize) + 1;const buckets = Array(bucketCount).fill().map(() => []);for (let i = 0; i < arr.length; i++) {const bucketIndex = Math.floor((arr[i] - min) / bucketSize);buckets[bucketIndex].push(arr[i]);}arr.length = 0;for (let i = 0; i < buckets.length; i++) {insertionSort(buckets[i]);arr.push(...buckets[i]);}return arr;
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(bucketSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:适用于均匀分布的数据。
时间复杂度:O(n + k),其中 n 是输入数组元素个数,k 是桶的个数。
- 基数排序(Radix Sort):按照位数将元素分配到不同的桶中,然后按顺序合并桶内的元素,重复执行直到所有位数排序完成。
function radixSort(arr) {const max = Math.max(...arr);const maxLength = String(max).length;let bucket = Array.from({ length: 10 }, () => []);for (let i = 0; i < maxLength; i++) {for (let j = 0; j < arr.length; j++) {const digit = Math.floor(arr[j] / 10 ** i) % 10;bucket[digit].push(arr[j]);}arr.length = 0;for (let k = 0; k < bucket.length; k++) {arr.push(...bucket[k]);bucket[k].length = 0;}}return arr;
}const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(radixSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]特点:适用于数字位数相同的整数排序。
时间复杂度:O(d * (n + k)),其中 d 是最大数字的位数,n 是输入数组元素个数,k 是输入范围大小。
每种排序算法都有不同的时间复杂度和适用场景。在实际应用中,根据数据规模和性能要求选择合适的排序算法是很重要的。
相关文章:

数据结构基础之排序算法
在数据结构中,常见的排序算法有以下几种: 冒泡排序(Bubble Sort):通过比较相邻元素并交换它们的位置,每轮将最大(或最小)的元素冒泡到末尾,重复执行直到排序完成。 fun…...
Spark(37):Streaming DataFrame 和 Streaming DataSet 创建
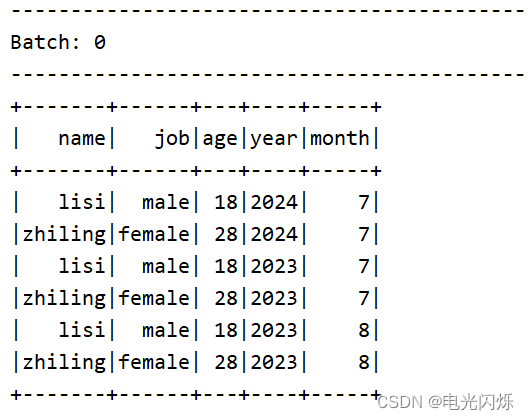
目录 0. 相关文章链接 1. 概述 2. socket source 3. file source 3.1. 读取普通文件夹内的文件 3.2. 读取自动分区的文件夹内的文件 4. kafka source 4.1. 导入依赖 4.2. 以 Streaming 模式创建 Kafka 工作流 4.3. 通过 Batch 模式创建 Kafka 工作流 5. Rate Source…...

SpringBoot集成Thymeleaf
Spring Boot 集成 Thymeleaf 模板引擎 1、Thymeleaf 介绍 Thymeleaf 是适用于 Web 和独立环境的现代服务器端 Java 模板引擎。 Thymeleaf 的主要目标是为开发工作流程带来优雅的自然模板,既可以在浏览器中正确显示的 HTML,也可以用作静态原型…...
:牛客在线编程03 二叉树)
算法练习(2):牛客在线编程03 二叉树
package jz.bm;import jz.TreeNode;import java.util.*;public class bm3 {/*** BM23 二叉树的前序遍历*/public int[] preorderTraversal (TreeNode root) {ArrayList<Integer> list new ArrayList<>();preOrder(root, list);int[] res new int[list.size()];fo…...

回归预测 | MATLAB实现TCN-BiLSTM时间卷积双向长短期记忆神经网络多输入单输出回归预测
回归预测 | MATLAB实现TCN-BiLSTM时间卷积双向长短期记忆神经网络多输入单输出回归预测 目录 回归预测 | MATLAB实现TCN-BiLSTM时间卷积双向长短期记忆神经网络多输入单输出回归预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现TCN-BiLSTM时间卷积…...
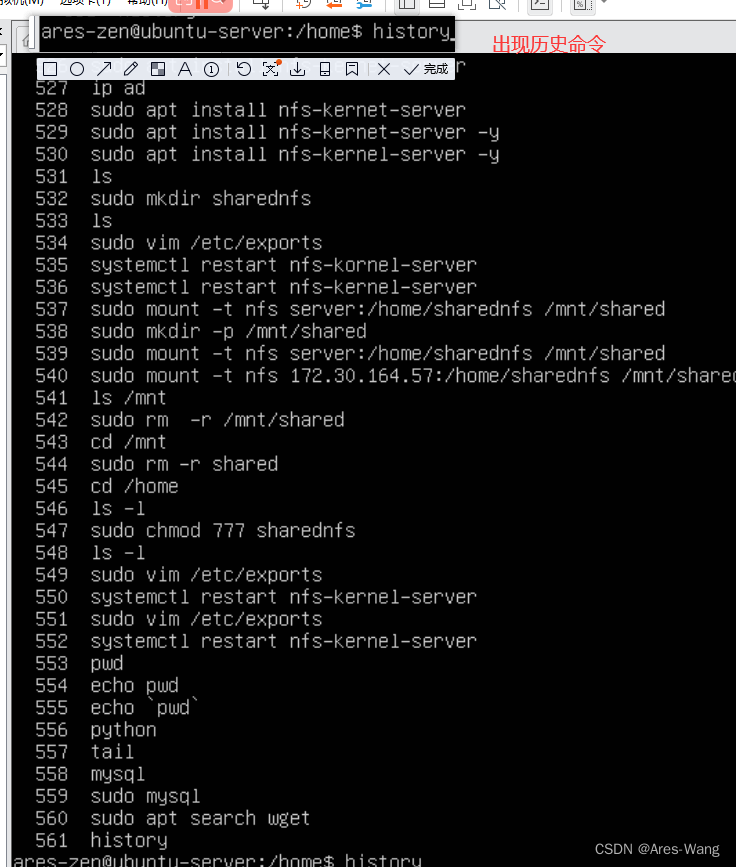
Linux 系列 常见 快捷键总结
强制停止 Ctrl C 退出程序、退出登录 Ctrl D 等价 exit 查看历史命令 history !命令前缀,自动匹配上一个命令 (历史命令中:从最新——》最老 搜索) ctrl r 输入内去历史命令中检索 # 回车键可以直接执行 ctrl a 跳到命令开头 …...
OA系统构建排座
目录 一.排座的介绍,作用 1.排座介绍 A.前端实现 B.数据库实现 C.后端实现 2.排座作用 A.座位预订 B.座位安排 C. 实时座位状态显示 二.利用Layui实现排座 1.基础版(通过htmlcssjs实现) A.基础版源码(html): 2.进阶版 …...

微信小程序 居中、居右、居底和横向、纵向布局,文字在图片中间,网格布局
微信小程序居中、居右、横纵布局 1、水平垂直居中(相对父类控件)方式一:水平垂直居中 父类控件: display: flex;align-items: center;//子控件垂直居中justify-content: center;//子控件水平居中width: 100%;height: 400px //注意…...

【C++】总结2
文章目录 1.final和override关键字2.extern "C"的用法3.野指针和垂悬指针(悬空指针)4.指针指向的内存被释放是什么意思5.C和C的类型安全6.C中的重载、重写(覆盖)和隐藏的区别 1.final和override关键字 final和override是C11引入的关键字&…...

vue2项目中使用svg图标
在开发项目的时候经常会用到svg矢量图,而且我们使用SVG以后,页面上加载的不再是图片资源, 这对页面性能来说是个很大的提升,而且我们SVG文件比img要小的很多,放在项目中几乎不占用资源。 1、安装SVG依赖插件并配置加载器和路径 npm instal…...
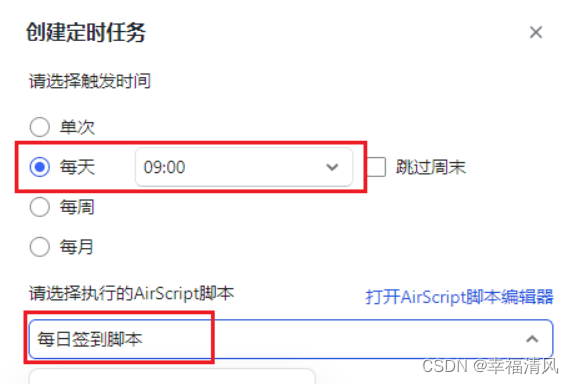
阿里云盘自动每日签到无需部署无需服务器(仅限学习交流使用)
一、前言 阿里云盘自动每日签到,无需部署,无需服务器 执行思路:使用金山文档的每日定时任务,执行阿里云盘签到接口。 二、效果展示: 三、步骤: 1、进入金山文档网页版 金山文档官网:https:…...
Blazor前后端框架Known-V1.2.7
V1.2.7 Known是基于C#和Blazor开发的前后端分离快速开发框架,开箱即用,跨平台,一处代码,多处运行。 Gitee: https://gitee.com/known/KnownGithub:https://github.com/known/Known 概述 基于C#和Blazor…...
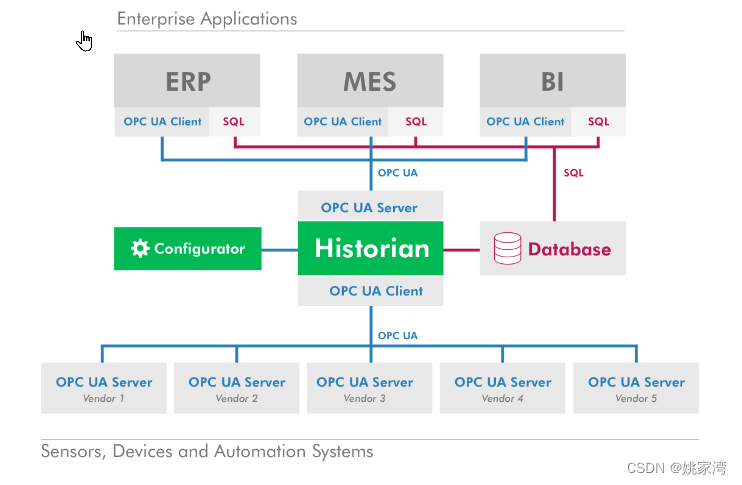
工业边缘计算为什么?
在工厂环境中使用边缘计算并不新鲜。可编程逻辑控制器(PLC)、微控制器、服务器和PC进行本地数据处理,甚至是微型数据中心都是边缘技术,已经在工厂系统中存在了几十年。在车间里看到的看板系统,打卡系统,历史…...
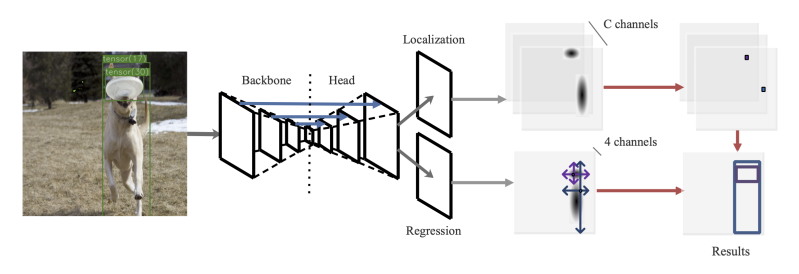
Training-Time-Friendly Network for Real-Time Object Detection 论文学习
1. 解决了什么问题? 目前的目标检测器很少能做到快速训练、快速推理,并同时保持准确率。直觉上,推理越快的检测器应该训练也很快,但大多数的实时检测器反而需要更长的训练时间。准确率高的检测器大致可分为两类:推理时…...

HTTP改HTTPS
tomcat中http协议改https 第一步,配置server.xml <?xml version"1.0" encoding"UTF-8"?> <Server port"8005" shutdown"SHUTDOWN"><Listener className"org.apache.catalina.startup.VersionLogger…...
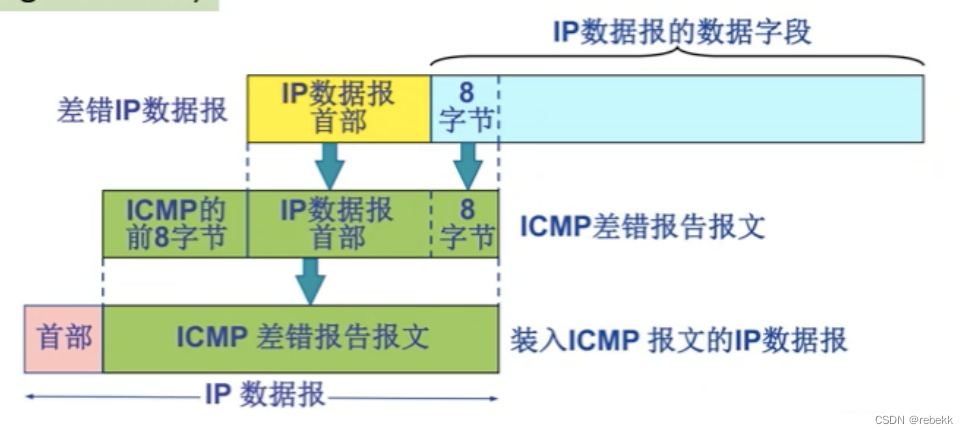
网络层中一些零碎且易忘的知识点
异构网络:指传输介质、数据编码方式、链路控制协议以及数据单元格式和转发机制不同,异构即物理层和数据链路层均不同RIP、OSPF、BGP分别是哪一层的协议: -RIPOSPFBGP所属层次应用层网络层应用层封装在什么协议中UDPIPTCP 一个主机可以有多个I…...
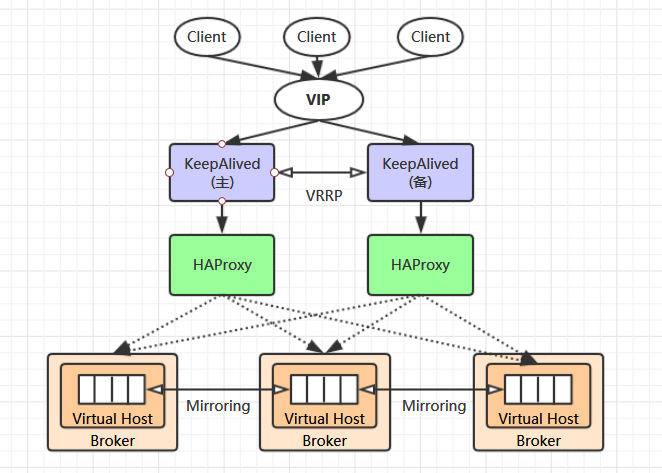
【RabbitMQ】之高可用集群搭建
目录 一、RabbitMQ 集群原理 1、默认集群原理2、镜像集群原理3、负载均衡方案 二、RabbitMQ 高可用集群搭建 1、RabbitMQ 集群搭建2、配置镜像队列3、HAProxy 环境搭建4、Keepalived 环境搭建 一、RabbitMQ 集群简介 1、默认集群原理 3-1、RabbitMQ 集群简介 单台 RabbitM…...
【node.js】01-fs读写文件内容
目录 一、fs.readFile() 读取文件内容 二、fs.writeFile() 向指定的文件中写入内容 案例:整理txt 需求: 代码: 一、fs.readFile() 读取文件内容 代码: //导入fs模块,从来操作文件 const fs require(fs)// 2.调…...

GitHub仓库如何使用
核心:GitHub仓库如何使用 目录 1.创建仓库: 2.克隆仓库到本地: 3.添加、提交和推送更改: 4.分支管理: 5.拉取请求(Pull Requests): 6.合并代码: 7.其他功能&…...

雪花算法,在分布式环境下实现高效的ID生成
其实雪花算法比较简单,可能称不上什么算法就是一种构造UID的方法。 点1:UID是一个long类型的41位时间戳,10位存储机器码,12位存储序列号。 点2:时间戳的单位是毫秒,可以同时链接1024台机器,每台…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
