运筹系列83:使用分枝定界求解tsp问题
1. 辅助函数
Node算子用来存储搜索树的状态。其中level等于path的长度,path是当前节点已经访问过的vertex清单,bound则是当前的lb。
这里的bound函数是一种启发式方法,等于当前路径的总长度,再加上往后走两步的最小值。
struct Nodelevel::Intpath::Vector{Int64} bound::Int
endfunction totaldist(adj_mat::Array{Int64,2},t::Vector{Int64} )n = length(t)sum([adj_mat[t[i],t[i+1]] for i in 1:n-1])+adj_mat[t[n],t[1]]
endfunction bound(adj_mat::Array{Int64,2}, path::Vector{Int64} )_bound = 0n = size(adj_mat)[1]determined, last = path[1:end-1], path[end]remain = setdiff(1:n,path)for i in 1:length(path)-1;_bound += adj_mat[path[i],path[i + 1]];end_bound += minimum([adj_mat[last,i] for i in remain])p = [path[1];remain]for r in remain_bound+=minimum([adj_mat[r,i] for i in setdiff(p,r)])endreturn _bound
end;
2. 分枝定界代码
这里用priorityQueue存储节点,用Queue也是一样的。
分枝条件为bound<ub,往下搜索所有没有探访过的节点,使用函数setdiff(1:n,v.path)。当然这里可以尝试将搜索范围缩小,比如仅搜索最近的一些节点,不过就不保证最优性了。
当搜索到level==n-1时,获得一个可行解,并且停止往下探索。此时如果路径长度比ub还短,则更新ub。
function solve(adj_mat::Array{Int64,2},ub::Int64 = 10^9)optimal_tour = Vector{Int64}()optimal_length = 0n = size(adj_mat)[1]PQ = PriorityQueue{Node,Int}()path = Vector{Int64}([1])v = Node(1,path,bound(adj_mat,path))enqueue!(PQ,v,v.bound) while length(PQ)>0v = dequeue!(PQ)if v.bound<ublevel = v.level+1b = 0for i in setdiff(1:n,v.path)path = [v.path;i]if level==n-1 #终止条件push!(path,setdiff(1:n,path)[1])_len = totaldist(adj_mat,path)if _len < ubub = _lenoptimal_length = _lenoptimal_tour = pathendelse # 进行分叉b = bound(adj_mat,path)if b < ub # 分枝条件enqueue!(PQ,Node(level,path,b),b)endendendendendoptimal_tour,optimal_length
end
solve([0 14 4 10 20;14 0 7 8 7;4 5 0 7 16;11 7 9 0 2;18 7 17 4 0])
输出([1, 4, 5, 2, 3], 30)。
TSP时一个NPhard问题,当点数增多时,使用b&b的算法性能会急速下降。
相关文章:

运筹系列83:使用分枝定界求解tsp问题
1. 辅助函数 Node算子用来存储搜索树的状态。其中level等于path的长度,path是当前节点已经访问过的vertex清单,bound则是当前的lb。 这里的bound函数是一种启发式方法,等于当前路径的总长度,再加上往后走两步的最小值。 struct …...
linux 指令 第3期
cat cat 指令: 首先我们知道一个文件内容属性 我们对文件操作就有两个方面:对文件内容和属性的操作 扩展:echo 指令 直接打印echo后面跟的字符串 看: 这其实是把它打印到了显示器上,我们也可以改变一下它的打印位置…...
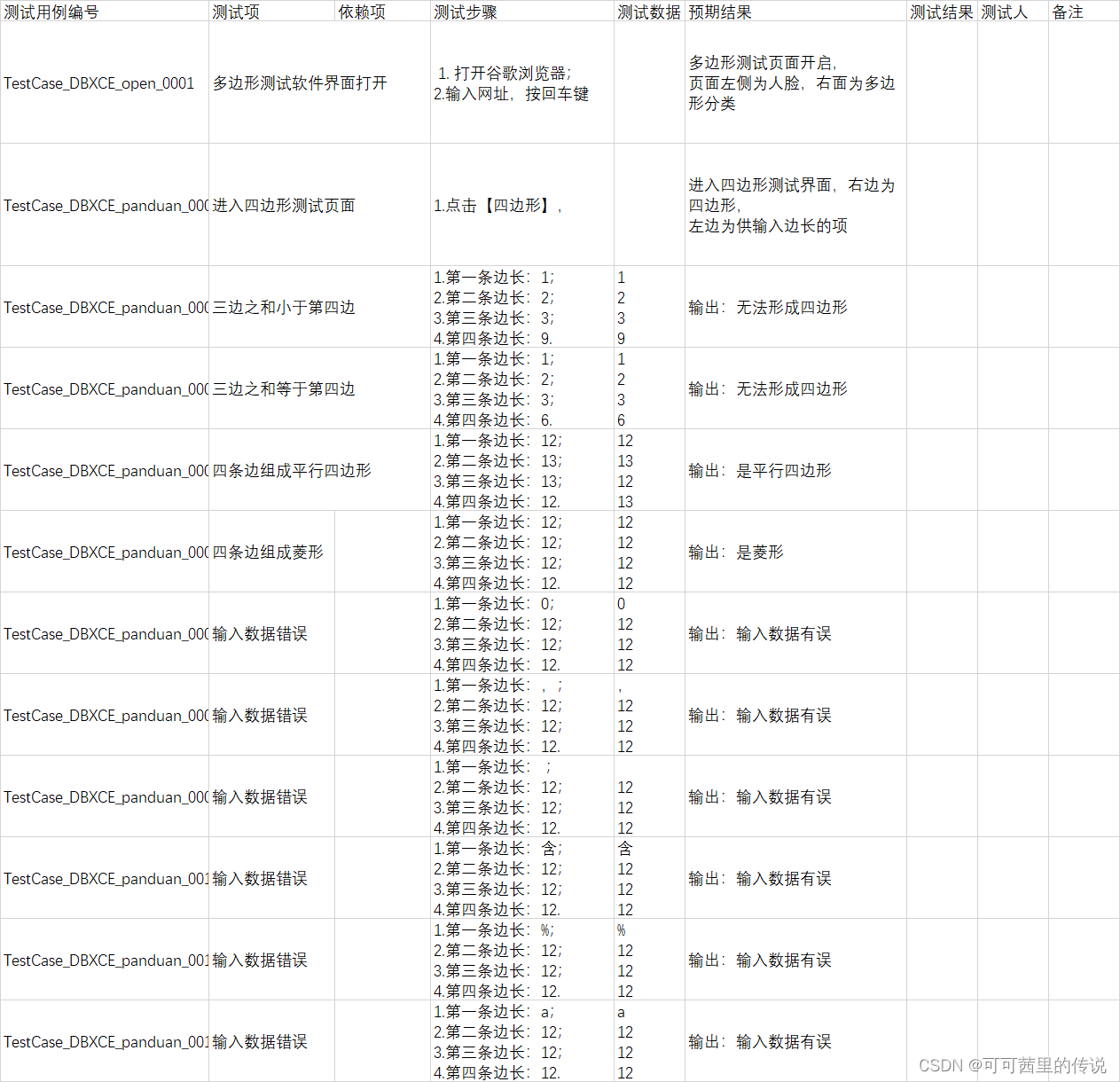
测试用例实战
测试用例实战 三角形判断 三角形测试用例设计 测试用例编写 先做正向数据,再做反向数据。 只要有一条边长为0,那就是不符合要求,不需要再进行判断,重复。 四边形 四边形测试用例...

Unity XML1——XML基本语法
一、XML 概述 全称:可拓展标记语言(EXtensible Markup Language) XML 是国际通用的,它是被设计来用于传输和存储数据的一种文本特殊格式,文件后缀一般为 .xml 我们在游戏中可以把游戏数据按照 XML 的格式标…...

了解Unity编辑器之组件篇Playables和Rendering(十)
Playables 一、Playable Director:是一种用于控制和管理剧情、动画和音频的工具。它作为一个中央控制器,可以管理播放动画剧情、视频剧情和音频剧情,以及它们之间的时间、顺序和交互。 Playable Director组件具有以下作用: 剧情控…...
python的包管理器pip安装经常失败的解决办法:修改pip镜像源
pip 常用的国内镜像源: https://pypi.tuna.tsinghua.edu.cn/simple/ // 清华 http://mirrors.aliyun.com/pypi/simple/ // 阿里云 https://pypi.mirrors.ustc.edu.cn/simple/ // 中国科技大学 http://pypi.hustunique.com/ // 华中理…...
忘记安卓图案/密码锁如何解锁?
如何解锁Android手机图案锁?如何删除忘记的密码?Android 手机锁定后如何重置?这是许多智能手机用户在网上提出的几个问题。为了回答这些问题,我们想出了一些简单有效的方法来解锁任何设备而不丢失数据。 忘记手机密码可能会令人恐…...
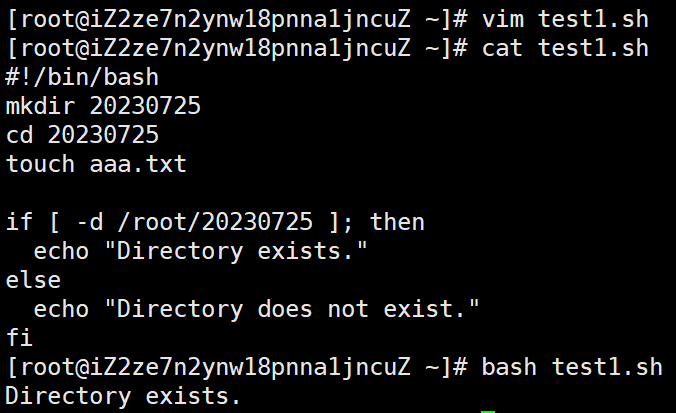
Bash编程
目录: bash编程语法bash脚本编写 1.bash编程语法 Bash 编程基础 变量引号数组控制语句函数 Bash 变量 语法: Variable_namevalue Bash 变量定义的规则 变量名区分大小写,a和A为两个不同的变量。变量名可以使用大小写字母混编的形式进行…...

vue指令-v-model修饰符
vue指令-v-model修饰符 1、目标2、语法 1、目标 让v-modelv-mode拥有更强大的功能 2、语法 v-model.修饰符“Vue数据变量” .number 以parseFloat转成数字类型 .trime 去除首位空白字符 .lazy 在change时触发而非input时示例1 <template><div id"app"&g…...

【论文精读CVPR_2023】3D-Aware Face Swapping
【论文精读CVPR_2023】3D-Aware Face Swapping 前言Abstract1. Introduction2. Related WorkFace Swapping.3D-Aware Generative Models.GAN Inversion.3. Method3.1. Overview3.2. Inferring 3D Prior from 2D Images3.3. Face Swapping via Latent Code Manipulation3.4. Joi…...

flutter开发实战-自定义相机camera功能
flutter开发实战-自定义相机camera功能。 Flutter 本质上只是一个 UI 框架,运行在宿主平台之上,Flutter 本身是无法提供一些系统能力,比如使用蓝牙、相机、GPS等,因此要在 Flutter 中调用这些能力就必须和原生平台进行通信。 实现…...

重排链表——力扣143
文章目录 题目描述法一:寻找链表中点、链表逆序、链表合并 题目描述 法一:寻找链表中点、链表逆序、链表合并 void reorderList(ListNode* head){if(headnullptr){return;}// 找到中点 ListNode* mid FindMiddle(head);ListNode *h1head, *h2mid->ne…...
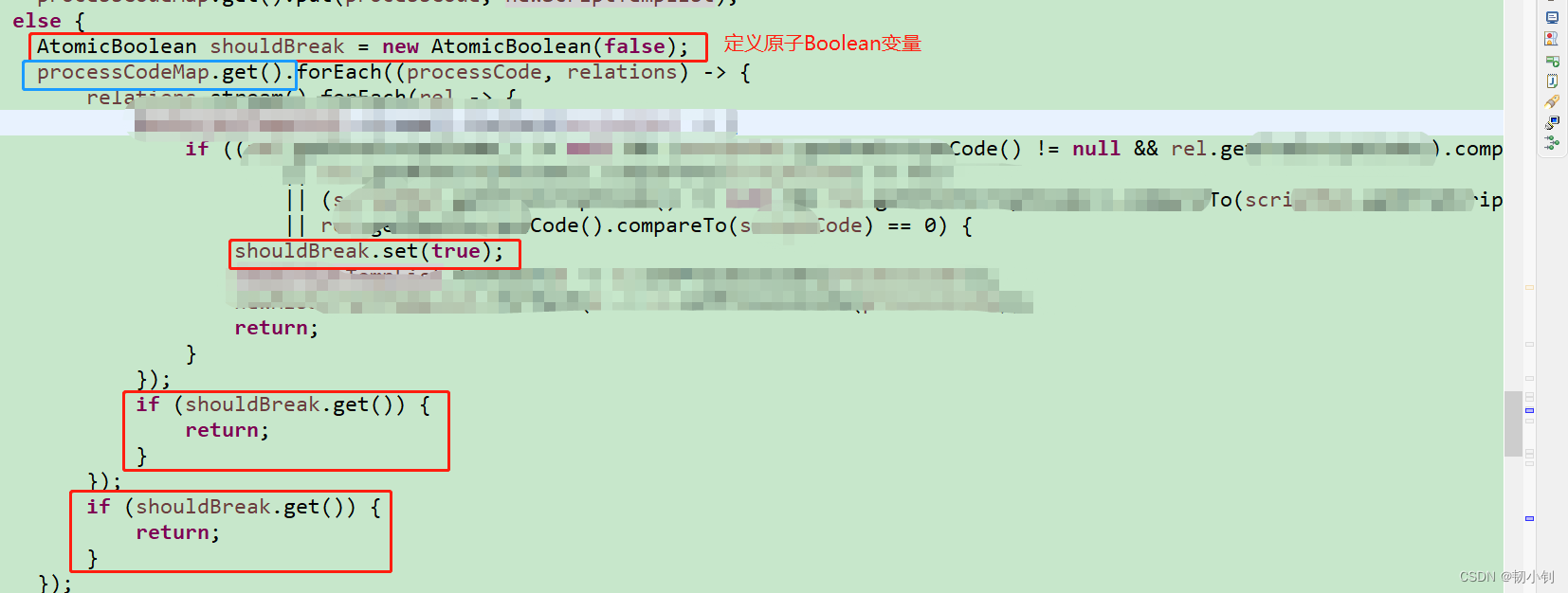
Lambda表达式常见的Local variable must be final or effectively final原因及解决办法
目录 Local variable must be final or effectively final错误原因 解决办法按照要求定义为final(不符合实情,很多时候是查库获取的变量值)使用原子类存储变量,保证一致性AtomicReference常用原子类 其它 Local variable must be …...

YOLOv5改进系列(16)——添加EMA注意力机制(ICASSP2023|实测涨点)
【YOLOv5改进系列】前期回顾: YOLOv5改进系列(0)——重要性能指标与训练结果评价及分析 YOLOv5改进系列(1)——添加SE注意力机制 YOLOv5改进系列(2)——添加...
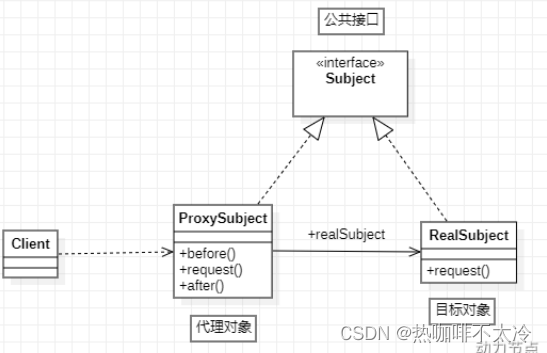
[SSM]GoF之代理模式
目录 十四、GoF之代理模式 14.1对代理模式的理解 14.2静态代理 14.3动态代理 14.3.1JDK动态代理 14.3.2CGLIB动态代理 十四、GoF之代理模式 14.1对代理模式的理解 场景:拍电影的时候,替身演员去代理演员完成表演。这就是一个代理模式。 演员为什…...
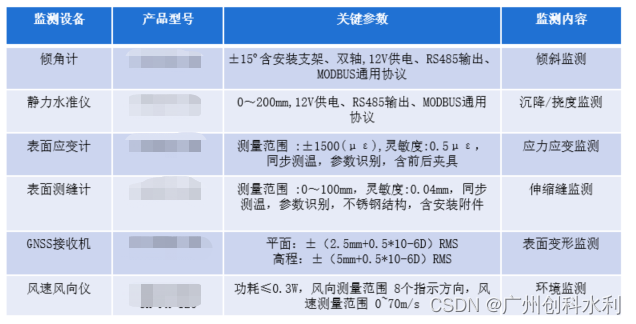
桥梁安全生命周期监测解决方案
一、方案背景 建筑安全是人们生产、经营、居住等经济生活和人身安全的基本保证,目前我国越来越多的建筑物逐 步接近或者已经达到了使用年限,使得建筑物不断出现各种安全隐患,对居民的人身安全和财产安全产 生不利影响,因此房…...
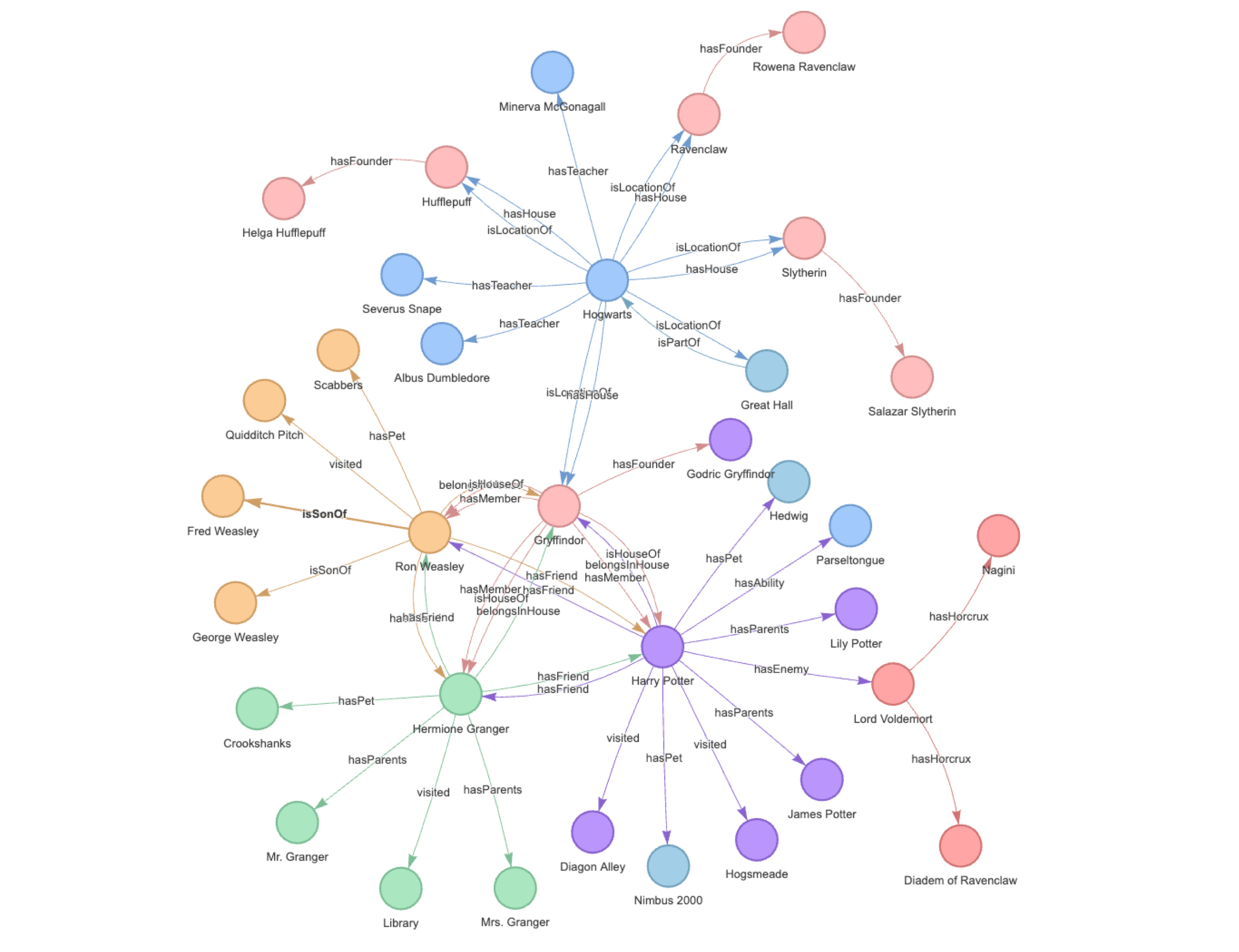
图技术在 LLM 下的应用:知识图谱驱动的大语言模型 Llama Index
LLM 如火如荼地发展了大半年,各类大模型和相关框架也逐步成型,可被大家应用到业务实际中。在这个过程中,我们可能会遇到一类问题是:现有的哪些数据,如何更好地与 LLM 对接上。像是大家都在用的知识图谱,现在…...
)
SpringBoot自动配置、启动器原理爆肝解析(干货满满)
文章目录 前言一、SpringBoot优势概要二、SpringBoot自动配置1. ☠注意☠2.自动配置详解 三、Starter(场景启动器)原理总结 前言 本文详细解析面试重点—SpringBoot自动配置原理、场景启动器原理,深入源码,直接上干货、绝不拖泥带…...

chrome扩展控制popup页面动态切换
文章目录 1、通过控制元素的显示隐藏达到popup页面切换的效果2、通过监听页面重新加载完成不同popup的切换3、直接修改popup页面location.href,无需刷新页面 1、通过控制元素的显示隐藏达到popup页面切换的效果 下面在mv2版本的API下完成 实际上通过控制页面元素实…...
:PyTorch常用函数)
【AI】《动手学-深度学习-PyTorch版》笔记(三):PyTorch常用函数
AI学习目录汇总 1、torch.arange 返回一维张量(一维数组),官网说明,常见的三种用法如下 输入:torch.arange(5) 输出:tensor([0, 1, 2, 3, 4]) 输入:torch.arange(5, 16) 输出:tensor([ 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]) 输入:torch.arange(1, 25, 2) …...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
