当前位置： 首页 > news >正文

移动零——力扣283

news 2025/11/3 23:34:22

题目描述

在这里插入图片描述

双指针

在这里插入图片描述

class Solution{
public:void moveZeroes(vector<int>& nums){int n = nums.size(), left=0, right=0;while(right<n){if(nums[right]){swap(nums[right], nums[left]);left++;}right++;}}
};

在这里插入图片描述

相关文章：

移动零——力扣283

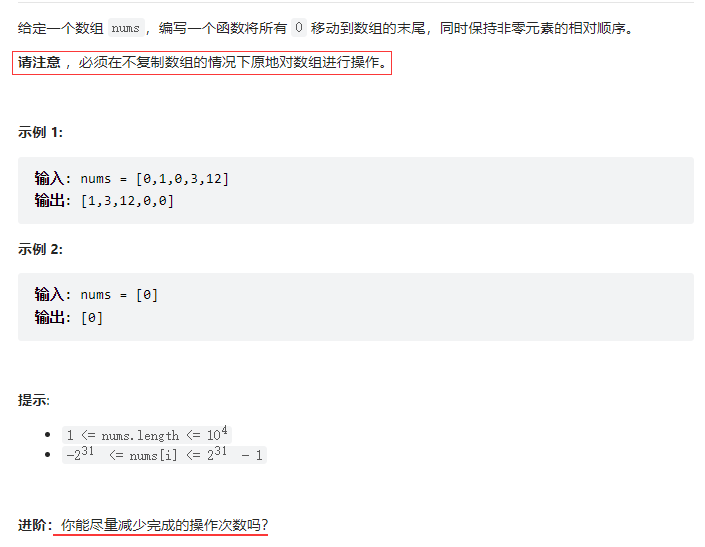
题目描述 双指针 class Solution{ public:void moveZeroes(vector<int>& nums){int n nums.size(), left0, right0;while(right<n){if(nums[right]){swap(nums[right], nums[left]);left;}right;}} };...

编程日记 2023/7/30 3:17:23

Transformer+MIA Future Work

TransformerMIA Future Work 主要的挑战和未来发展分为三个部分&#xff0c;即 1、特征集成和计算成本降低、 2、数据增强和数据集收集、 3、学习方式和模态-对象分布 1、特征集成和计算成本降低 为了同时捕获局部和全局特征来提高模型性能&#xff0c;目前大多数工作只是…...

编程日记 2023/7/30 3:16:20

深度学习入门（二）：神经网络整体架构

一、前向传播 作用于每一层的输入&#xff0c;通过逐层计算得到输出结果 二、反向传播 作用于网络输出&#xff0c;通过计算梯度由深到浅更新网络参数 三、整体架构 层次结构&#xff1a;逐层变换数据 神经元&#xff1a;数据量、矩阵大小&#xff08;代表输入特征的数量…...

编程日记 2023/7/30 3:15:18

rust 配置

rustup 镜像 在 cmd 中输入以下代码&#xff0c;设置环境变量 setx RUSTUP_UPDATE_ROOT https://mirrors.tuna.tsinghua.edu.cn/rustup/rustup setx RUSTUP_DIST_SERVER https://mirrors.tuna.tsinghua.edu.cn/rustupcrates.io 索引镜像 在 C:\Users\用户名\.cargo\config 文…...

编程日记 2023/7/30 3:14:17

文心一言 VS 讯飞星火 VS chatgpt （67）-- 算法导论6.5 6题

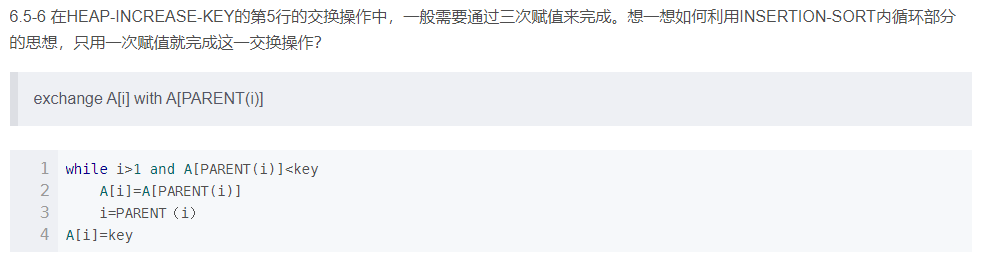
文心一言 VS 讯飞星火 VS chatgpt &#xff08;67&#xff09;-- 算法导论6.5 6题 六、在 HEAP-INCREASE-KEY 的第 5 行的交换操作中&#xff0c;一般需要通过三次赋值来完成。想一想如何利用INSERTION-SORT 内循环部分的思想&#xff0c;只用一次赋值就完成这一交换操作? 文…...

编程日记 2023/7/30 3:13:15

6、Kubernetes核心技术 - Pod

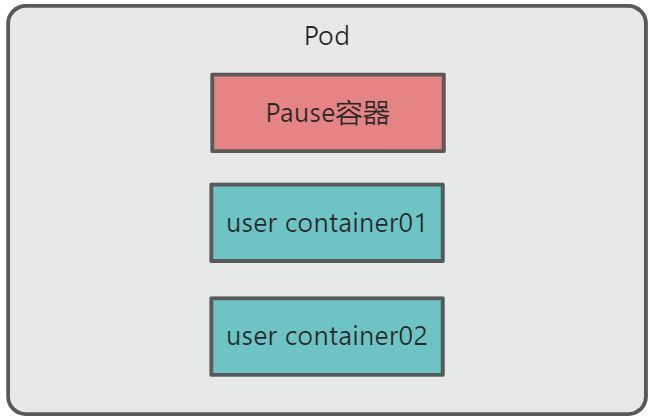
目录 一、概述 二、Pod机制 2.1、共享网络 2.2、共享存储 三、Pod资源清单 四、 Pod 的分类 五、Pod阶段 六、Pod 镜像拉取策略 ImagePullBackOff 七、Pod 资源限制 八、容器重启策略 一、概述 Pod 是可以在 Kubernetes 中创建和管理的、最小的可部署的计算单元。P…...

编程日记 2023/7/30 3:12:14

VlanIf虚拟接口 通信技术（二十三课）

一 Vlan技术之间的通信 单臂路由（One-Arm Routing）是一种网络架构设计方式，通常用于部署网络设备（如防火墙、负载均衡器等）实现网络流量控制和安全策略。在单臂路由中，网络设备只有一个物理接口与局域网（LAN）或广域网（WAN）相连。 1.2 交换机 数据链路层 （第二层）…...

编程日记 2023/7/30 3:11:11

图神经网络（GNN）入门学习笔记（直观且简单）

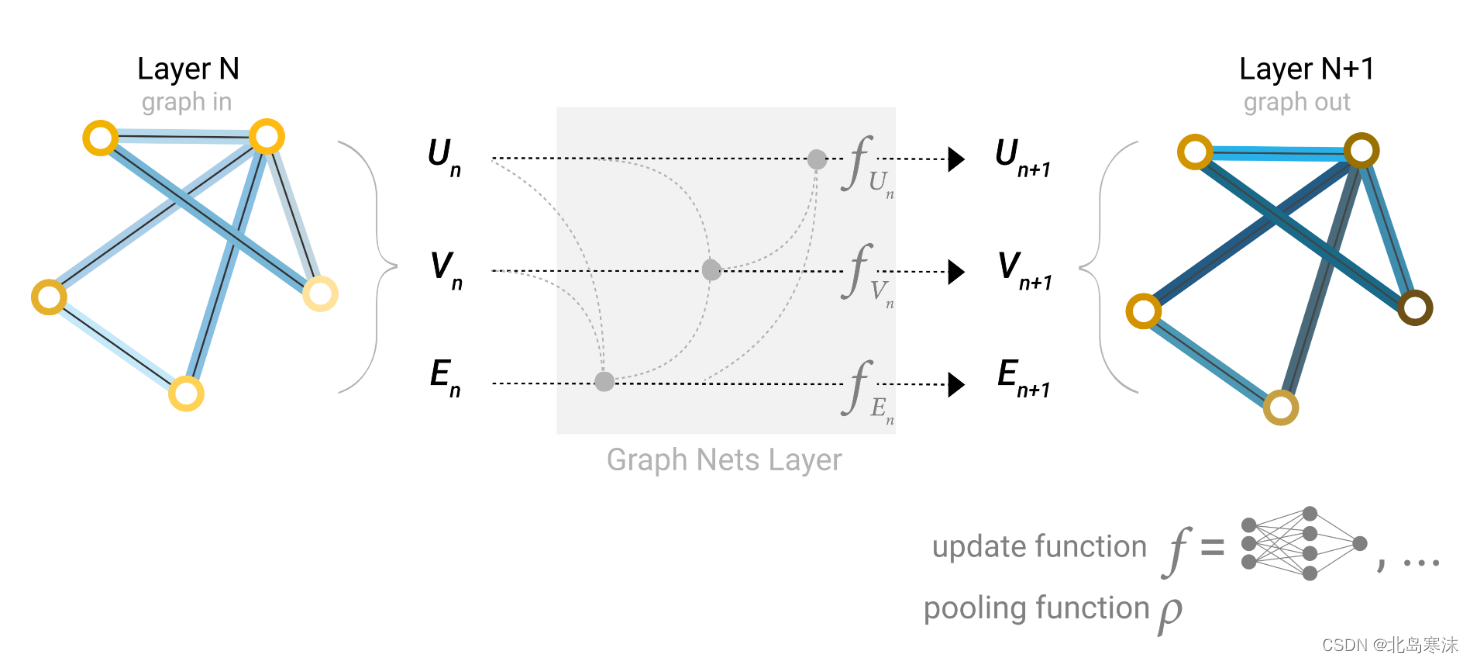
文章目录 图的定义和表示可以使用图数据结构的问题将图结构用于机器学习的挑战最基本的图神经网络概述汇聚操作基于信息传递的改进图神经网络全局向量信息的利用 本篇文章参考发表于Distill上的图神经网络入门博客&#xff1a; A Gentle Introduction to Graph Neural Network…...

编程日记 2023/7/30 3:10:10

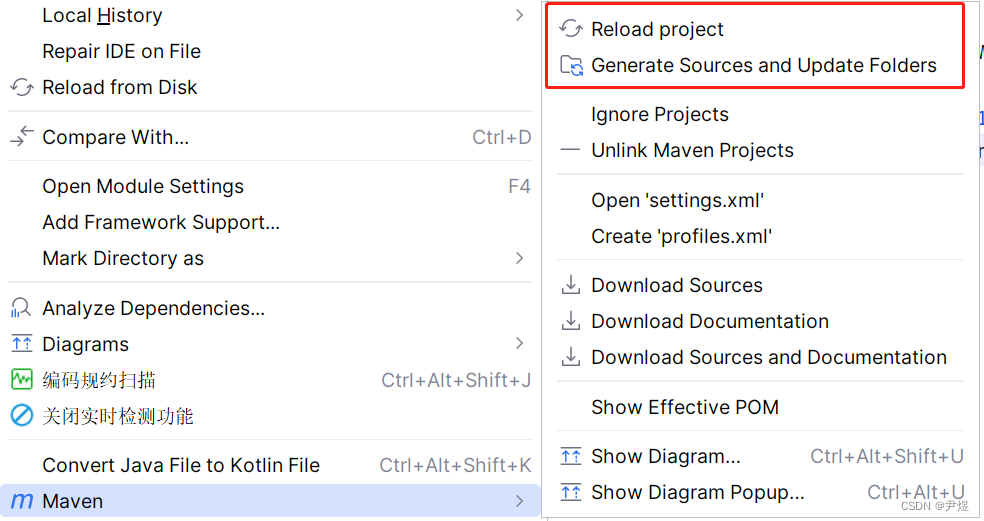
【Java开发】 Mybatis-Flex 01：快速入门

Mybatis 作为头部的 ORM 框架&#xff0c;他的增强工具可谓层出不穷&#xff0c;比如出名的 Mybatis-Plus 和 阿里云开源的 Fluent-MyBatis&#xff0c;如今出了一款 Mybatis-Flex &#xff0c;相比前两款功能更为强大、性能更为强悍&#xff0c;不妨来了解一下。 目录 1 Myba…...

编程日记 2023/7/30 3:09:08

企业级业务架构学习笔记＜二＞

一.业务架构基础 业务架构的定义 以实现企业战略为目标&#xff0c;构建企业整体业务能力规划并将其传导给技术实现端的结构化企业能力分析方法 (业务架构可以从企业战略触发&#xff0c;按照企业战略设计业务及业务过程&#xff0c;业务过程时需要业务能力支撑的&#xff0…...

编程日记 2023/7/30 3:08:08

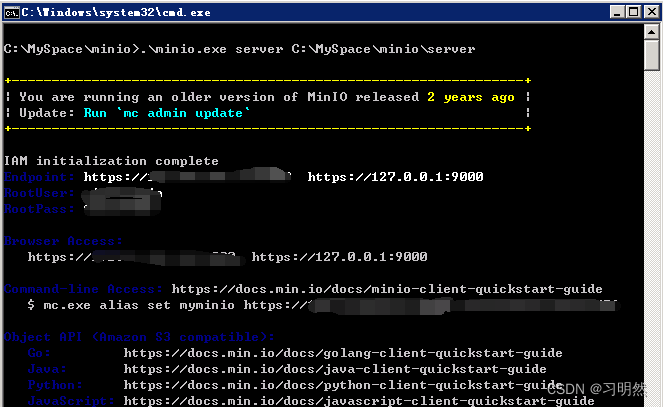
Minio在windows环境配置https访问

minio启动后&#xff0c;默认访问方式为http&#xff0c;但是有的时候我们的访问场景必须是https&#xff0c;浏览器有的会默认以https进行访问&#xff0c;这个时候就需要我们进行配置上的调整&#xff0c;将minio从http访问升级到https。而查看minio的官方文档&#xff0c;并…...

编程日记 2023/7/30 3:07:06

安装JDK环境(Windows+Linux双教程)

今日一语&#xff1a;今天的事情不去做&#xff0c;到了明天就成了麻烦&#xff0c;到了下个月就成了隐患&#xff0c;到了明年只剩下悔恨和惋惜 Linux 从Oracle网站下载linux的rpm包java -version 查询java环境是否已经安装 如果已经安装&#xff0c;可以选择卸载重装或者直接…...

编程日记 2023/7/30 3:06:05

SVG图标，SVG symbols，SVG use标签

SVG图标&#xff0c;SVG symbols 项目中图标的使用&#xff0c;趋势是使用svg作图标的&#xff0c;优点如下 兼容现有图片能力前提还支持矢量 可读性好&#xff0c;有利于SEO与无障碍 在性能和维护性方面也比iconfont要强很多 怎么在项目中优雅的使用svg图标&#xff0c;下面…...

编程日记 2023/7/30 3:05:03

常用css 笔记

0、定义变量 :root { --primary-color: #007bff;} .button { background-color: var(--primary-color);} 1、水平垂直居中 div {width: 100px;height: 100px;position: absolute;top: 0;right: 0;bottom: 0;left: 0;margin: auto; }父级控制子集居中 .parent {display: fle…...

编程日记 2023/7/30 3:04:02

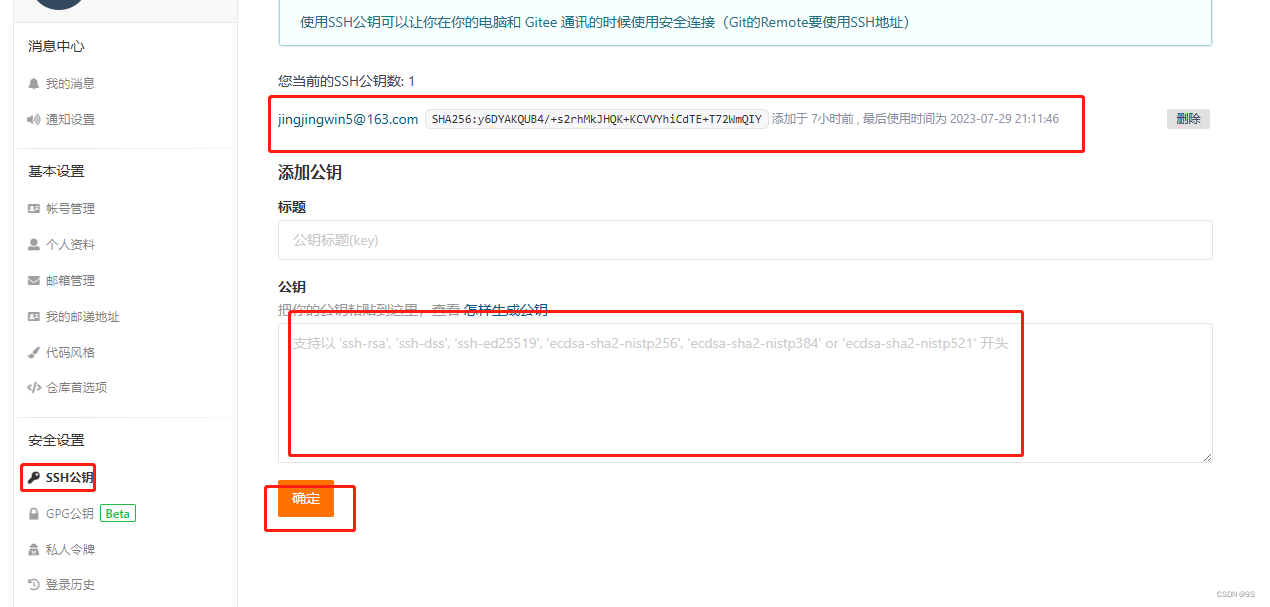
git的ssh方式对接码云

一、环境准备&#xff1a; 1、git下载&#xff0c;360管家或是百度。 2、vs2022&#xff0c;百度下载。 二、配置git&#xff1a; 1、打开准备存放文件的文件夹&#xff0c;右键&#xff0c;选择“Git Bash here”&#xff0c;弹出命令窗口&#xff0c; 输入&#xff1a;ss…...

编程日记 2023/7/30 3:03:01

Golang之路---02 基础语法——变量

Golang变量 变量的声明 声明变量的一般形式是使用 var 关键字 Go 语言是静态类型语言&#xff0c;编译时&#xff0c;编译器会检查变量的类型&#xff0c;所以要求所有的变量都要有明确的类型。 1 &#xff1a;一个变量单行声明 语法格式&#xff1a; var name type var是关…...

编程日记 2023/7/30 3:01:59

Webpack5 DefinePlugin的作用

在Webpack 5中&#xff0c;DefinePlugin是一个插件&#xff0c;用于创建全局常量&#xff0c;这些常量可以在编译过程中被引用。它的作用是允许开发人员在代码中定义全局变量&#xff0c;这些变量在构建过程中将被替换为其对应的值。 DefinePlugin并不是必须的&#xff0c;但它…...

编程日记 2023/7/30 3:00:58

Verilog语法学习——LV7_求两个数的差值

LV7_求两个数的差值 题目来源于牛客网 [牛客网在线编程_Verilog篇_Verilog快速入门 (nowcoder.com)](https://www.nowcoder.com/exam/oj?page1&tabVerilog篇&topicId301) 题目 描述 根据输入信号a,b的大小关系&#xff0c;求解两个数的差值&#xff1a;输入信号a,b…...

编程日记 2023/7/30 2:59:57

C#匿名函数，lambda表达式笔记

一.匿名函数 匿名函数是一种定义时不起函数名的技术&#xff0c;因此无法直接调用&#xff0c;通常用来赋值给委托后被委托调用。在匿名方法中您不需要指定返回类型&#xff0c;它是从方法主体内的 return 语句推断的 它的语法形式为&#xff1a;delegate (input-parameters)…...

编程日记 2023/7/30 2:58:55

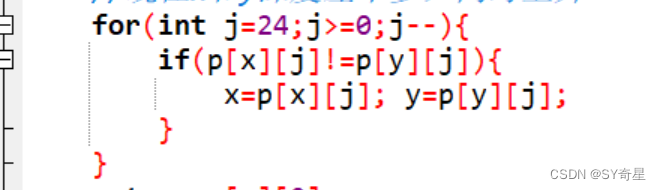
【图论】LCA（倍增）

一.LCA介绍 LCA通常指的是“最近共同祖先”&#xff08;Lowest Common Ancestor&#xff09;。LCA是一种用于解决树或图结构中两个节点的最低共同祖先的问题的算法。 在树结构中&#xff0c;LCA是指两个节点的最近层级的共同祖先节点。例如&#xff0c;考虑一棵树&#xff0c;…...

编程日记 2023/7/30 2:57:53

Python爬虫实战：研究MechanicalSoup库相关技术

一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库，专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力，提供了直观的 API，让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

编程新知 2025/10/10 18:13:55

FastAPI 教程：从入门到实践

FastAPI 是一个现代、快速&#xff08;高性能&#xff09;的 Web 框架&#xff0c;用于构建 API&#xff0c;支持 Python 3.6。它基于标准 Python 类型提示&#xff0c;易于学习且功能强大。以下是一个完整的 FastAPI 入门教程&#xff0c;涵盖从环境搭建到创建并运行一个简单的…...

编程新知 2025/10/16 7:51:26

《通信之道——从微积分到 5G》读书总结

第1章 绪 论 1.1 这是一本什么样的书 通信技术&#xff0c;说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号&#xff08;调制&#xff09; 把信息从信号中抽取出来&am…...

编程新知 2025/11/1 1:01:14

Keil 中设置 STM32 Flash 和 RAM 地址详解

文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面（Target 选项卡）1. IROM1（用于配置 Flash）2. IRAM1（用于配置 RAM）二、链接器设置界面（Linker 选项卡）1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数（如果没有勾选上面…...

编程新知 2025/11/1 15:26:54

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/10/13 2:26:14

Redis的发布订阅模式与专业的 MQ（如 Kafka, RabbitMQ）相比，优缺点是什么？适用于哪些场景？

Redis 的发布订阅&#xff08;Pub/Sub&#xff09;模式与专业的 MQ&#xff08;Message Queue&#xff09;如 Kafka、RabbitMQ 进行比较&#xff0c;核心的权衡点在于&#xff1a;简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

编程新知 2025/8/21 20:41:27

在Ubuntu24上采用Wine打开SourceInsight

1. 安装wine sudo apt install wine 2. 安装32位库支持，SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库（解决显示问题） sudo apt install fonts-wqy…...

编程新知 2025/10/14 0:47:25

网站指纹识别

网站指纹识别 网站的最基本组成&#xff1a;服务器&#xff08;操作系统&#xff09;、中间件&#xff08;web容器&#xff09;、脚本语言、数据厍 为什么要了解这些&#xff1f;举个例子&#xff1a;发现了一个文件读取漏洞&#xff0c;我们需要读/etc/passwd&#xff0c;如…...

编程新知 2025/10/25 12:55:59

Golang——9、反射和文件操作

反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一&#xff1a;使用Read()读取文件2.3、方式二&#xff1a;bufio读取文件2.4、方式三&#xff1a;os.ReadFile读取2.5、写…...

编程新知 2025/10/30 16:18:55

Ubuntu系统多网卡多相机IP设置方法

目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机&#xff0c;交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息&#xff0c;系统版本&#xff1a;Ubuntu22.04.5 LTS&#xff1b;内核版本…...

编程新知 2025/11/1 21:28:35