Computer Graphics From Scratch - Chapter 8
系列文章目录
简介:Computer Graphics From Scratch-《从零开始的计算机图形学》简介
第一章: Computer Graphics From Scratch - Chapter 1 介绍性概念
第二章:Computer Graphics From Scratch - Chapter 2 基本光线追踪
第三章:Computer Graphics From Scratch - Chapter 3 光照
第四章:Computer Graphics From Scratch - Chapter 4 阴影和反射
第五章:Computer Graphics From Scratch - Chapter 5 扩展光线追踪
第六章:Computer Graphics From Scratch - Chapter 6 线条
第七章:Computer Graphics From Scratch - Chapter 7 实心三角形
Chapter 8
- 系列文章目录
- Shaded Triangle - 阴影三角形
- 一、Defining Our Problem - 定义我们的问题
- 二、Computing Edge Shading - 计算边缘着色
- 三、Computing Interior Shading - 计算内部着色
- 四、Summary - 概括
Shaded Triangle - 阴影三角形
In the previous chapter, we developed an algorithm to draw a triangle filled with a solid color. Our goal for this chapter is to draw a shaded triangle—that is, a triangle filled with a color gradient.
在上一章中,我们开发了一种算法来绘制填充有纯色的三角形。本章的目标是绘制一个带阴影的三角形,即一个填充有颜色渐变的三角形。
一、Defining Our Problem - 定义我们的问题
我们想用单一颜色的不同色调填充三角形。它会看起来如图8-1. shades 色调

图8-1:一个着色的三角形
我们需要一个更正式的定义来定义我们试图绘制的内容。我们有一个基色C:例如,(0,255,0)(0,255,0)(0,255,0) 纯绿色。我们将为每个顶点分配一个实值 hhh,表示顶点处颜色的强度。hhh 在 [0.0,1.0][0.0, 1.0][0.0,1.0] 范围内,其中 0.00.00.0 表示最暗的阴影(即黑色),1.01.01.0 表示尽可能亮的阴影(即原始颜色),而不是白色!
为了计算给定三角形 C 的基色和该像素 hhh 处的强度的像素的确切色调,我们将逐通道相乘:
Ch=(RC⋅h,GC⋅h,BC⋅h)C_h = (R_C · h, G_C · h, B_C · h)Ch=(RC⋅h,GC⋅h,BC⋅h)
因此,h=0.0h = 0.0h=0.0 产生纯黑色,h=1.0h = 1.0h=1.0 产生原始颜色 C,h=0.5h = 0.5h=0.5 产生的颜色是原始颜色的一半亮度。
二、Computing Edge Shading - 计算边缘着色
为了绘制一个带阴影的三角形,我们需要做的就是为三角形的每个像素计算一个 hhh 值,计算相应的颜色阴影,然后绘制像素。
然而,在这一点上,我们只知道三角形顶点的 hhh 值,因为我们选择了它们。我们如何计算三角形其余部分的 hhh 值?
让我们从三角形的边缘开始。考虑边缘 ABABAB。我们知道hAh_AhA和hBh_BhB。在 ABABAB 的中点 MMM 处会发生什么?
由于我们希望强度从 AAA 到 BBB 平滑变化,因此 hMh_MhM 的值必须在 hAh_AhA 和hBh_BhB之间。既然 MMM 在 ABABAB 的中间,为什么不选择 hMh_MhM 在 hAh_AhA 和hBh_BhB的中间,也就是它们的平均值呢?
更正式地说,我们有一个函数 h=f(P)h = f(P)h=f(P),它给每个点 PPP 一个强度值 hhh; 我们知道它在 AAA 和 BBB 处 fff 分别的值,h(A)=hAh(A) = h_A h(A)=hA和 h(B)=hBh(B)= h_Bh(B)=hB
我们希望这个函数是平滑的。由于我们对 h=f(P)h = f(P)h=f(P)一无所知,因此我们可以选择任何与我们所知的函数兼容的函数,例如线性函数(图8-2)。
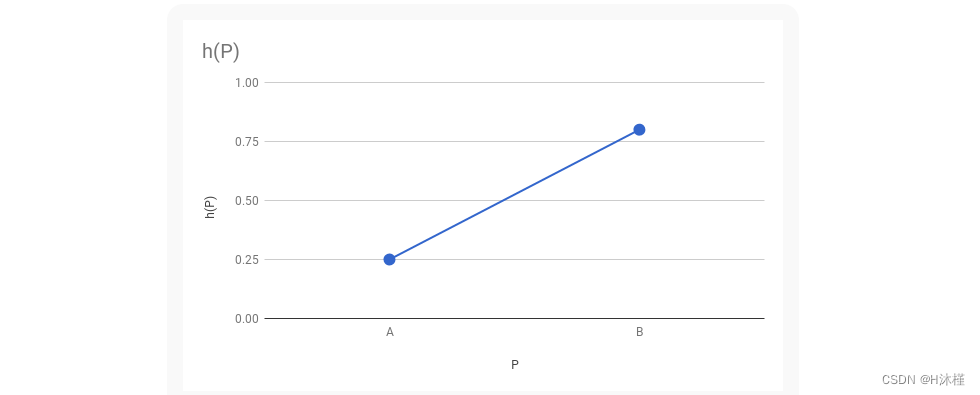
Figure 8-2: A linear function h§, compatible with what we know about h(A) and h(B)
这与前一章的情况非常相似:我们有一个线性函数 x=f(y)x = f(y)x=f(y)
我们知道这个函数在三角形顶点的值,我们想计算沿其边的 xxx 值。
我们可以以非常相似的方式沿三角形的边 计算 hhh 的值,使用 以 yyy 作为自变量的插值(我们知道)和 hhh 作为因变量(我们想要的值):
x01 = Interpolate(y0, x0, y1, x1)
h01 = Interpolate(y0, h0, y1, h1)x12 = Interpolate(y1, x1, y2, x2)
h12 = Interpolate(y1, h1, y2, h2)x02 = Interpolate(y0, x0, y2, x2)
h02 = Interpolate(y0, h0, y2, h2)
接下来,我们将 xxx 数组连接为**“短”**边,然后确定 x02 和 x012 中的哪一个x_left,哪个x_right。同样,我们可以在这里对 hhh 向量做一些非常相似的事情。
但是,我们将始终使用 xxx 值来确定哪一侧是左边,哪一侧是右边,hhh 值只会“跟随”。
xxx 和 hhh 是屏幕上实际点的属性,因此我们不能自由混合搭配左右两侧的值。
我们可以按如下方式编码:
// Concatenate the short sides
remove_last(x01)
x012 = x01 + x12remove_last(h01)
h012 = h01 + h12// Determine which is left and which is right
m = floor(x012.length / 2)
if x02[m] < x012[m]
{x_left = x02h_left = h02x_right = x012h_right = h012
}
else
{x_left = x012h_left = h012x_right = x02h_right = h02
}
这与上一章(示例 7-1)中代码的相关部分非常相似,只是每次我们使用 xxx 向量做某事时,我们对相应的 hhh 向量执行相同的操作。
三、Computing Interior Shading - 计算内部着色
最后一步是绘制实际的水平 段 。对于每个细分 段 ,我们知道 x_left 和 x_right ,如上一章所述; 现在我们也知道 h_left 和 h_right 。但这次我们不能只是从左到右迭代并用基色绘制每个像素:我们需要为这个 段 的每个像素计算 hhh 值。
同样,我们可以假设 hhh随 xxx 线性变化,并使用插值来计算这些值。在这种情况下,自变量是xxx,它从我们着色的特定水平 段 的 x_left 值变为 x_right 值;
因变量为hhh,其对应的 x_left 和 x_right 值为该段的 h_left 和 h_right:
x_left_this_y = x_left[y - y0]
h_left_this_y = h_left[y - y0]x_right_this_y = x_right[y - y0]
h_right_this_y = h_right[y - y0]h_segment = Interpolate(x_left_this_y, h_left_this_y,x_right_this_y, h_right_this_y)
或者,用更紧凑的方式表示:
h_segment = Interpolate(x_left[y - y0], h_left[y - y0],x_right[y - y0], h_right[y - y0])
现在只需计算每个像素的颜色并绘制它!示例 8-1 显示了 DrawShadedTriangle 的完整伪代码。
DrawShadedTriangle (P0, P1, P2, color)
{❶ // Sort the points so that y0 <= y1 <= y2if y1 < y0 { swap(P1, P0) }if y2 < y0 { swap(P2, P0) }if y2 < y1 { swap(P2, P1) }// Compute the x coordinates and h values of the triangle edgesx01 = Interpolate(y0, x0, y1, x1)h01 = Interpolate(y0, h0, y1, h1)x12 = Interpolate(y1, x1, y2, x2)h12 = Interpolate(y1, h1, y2, h2)x02 = Interpolate(y0, x0, y2, x2)h02 = Interpolate(y0, h0, y2, h2)// Concatenate the short sidesremove_last(x01)x012 = x01 + x12remove_last(h01)h012 = h01 + h12// Determine which is left and which is rightm = floor(x012.length / 2)if x02[m] < x012[m] {x_left = x02h_left = h02x_right = x012h_right = h012} else {x_left = x012h_left = h012x_right = x02h_right = h02}// Draw the horizontal segments❷ for y = y0 to y2 {x_l = x_left[y - y0]x_r = x_right[y - y0]❸ h_segment = Interpolate(x_l, h_left[y - y0], x_r, h_right[y - y0])for x = x_l to x_r {❹ shaded_color = color * h_segment[x - x_l]canvas.PutPixel(x, y, shaded_color)}}
}
Listing 8-1: A function for drawing shaded triangles
该函数的伪代码与上一章(示例7-1)中开发的函数非常相似。
在水平段循环之前❷, 我们以类似的方式操纵 xxx 向量和 hhh 向量,如上所述。
在循环中,我们有一个额外的调用Interpolate❸ 以计算当前水平段中每个像素的hhh值。
最后,在内部循环中,我们使用hhh的插值来计算每个像素的颜色❹.
注意,我们对三角形顶点的排序与之前一样❶. 然而,我们现在认为这些顶点及其属性(如强度值 hhh )是一个不可分割的整体;也就是说,交换两个顶点的坐标也必须交换它们的属性。
您可以在以下位置找到此算法的实时实现 https://gabrielgambetta.com/computer-graphics-from-scratch/demos/raster-04.html
四、Summary - 概括
在本章中,我们扩展了上一章中开发的三角形绘制代码,以支持平滑着色的三角形。请注意,我们仍然可以使用它来绘制单色三角形,方法是使用 1.0 作为所有三个顶点的 hhh 值。
这个算法背后的想法实际上比看起来更通用。hhh 是强度值的事实对算法的“形状”没有影响; 我们只在最后,当我们要调用 PutPixel 时,才为这个值赋予意义。这意味着我们可以使用此算法来计算三角形顶点的任何属性的值,对于三角形的每个像素,只要我们假设该值在屏幕上线性变化。
在接下来的章节中,我们确实会使用这个算法来改善三角形的视觉外观。
然而,在下一章中,我们要绕道而行。掌握了在2D画布上绘制三角形后,我们将把注意力转向三维。
.
相关文章:

Computer Graphics From Scratch - Chapter 8
系列文章目录 简介:Computer Graphics From Scratch-《从零开始的计算机图形学》简介 第一章: Computer Graphics From Scratch - Chapter 1 介绍性概念 第二章:Computer Graphics From Scratch - Chapter 2 基本光线追踪 第三章:Computer Gr…...

金三银四”不香了?
“金三银四”不香了? “金三银四”这个词,放在三年前,勾勒的是无数踌躇满志的年轻人涌向职场,大中小企业血液更新与流动的鲜活画面。 尤其是互联网行业,这个在过去20多年里极大改变文化交流方式与商业形态的领域&…...

个人开源PCB开发板列表汇总
个人开源PCB开发板列表汇总✨首先感谢立创EDA的免费打样和立创一起开源的广大网页。 🔰STC单片机为主控开源PCB开发板列表 📌STC15F2K60S2开发板:https://oshwhub.com/perseverance51/stc15f2k60s2-ji-tong-ban 📌STC15W408AS系…...

2023美国大学生数学建模竞赛(美赛)思路代码
2023美国大学生数学建模竞赛(美赛)思路&代码报名时间节点比赛说明问题A(数据分析题):收干旱影响的植物群落(MCM)第一问第二问问题B(仿真建模题):重塑马赛…...

makefile简易教程
makefile简易教程 一、学习目标 达到多文件快速编译的需求,相关符号的意思,以及其它注意事项。 二、快速入门 2.1 基本概念 Makefile 是一个在Unix和Linux操作系统上使用的构建工具,用于自动化编译和构建源代码。 2.2 用处 通过Makefi…...

快速入门nginx
目录 1.nginx前言 2.什么是nginx 3.Nginx作用? 1.正向代理 2.反向代理 3.轮询 4.加权轮询 4.Nginx的安装 1.windows下安装 2.linux下安装 5.Nginx常用命令 1.nginx前言 我们公司项目刚刚上线的时候,并发量小,用户使用的少&#…...

甘特图:项目管理工具,轻松简化工作流程
项目规模越大,管理就越复杂,有时候甚至一个项目经理需要管理多个项目,当多个项目、多条任务同时进行,项目所涉及的范围广,内容越来越复杂,使得项目越难以把控,好的管理工具,可以提升…...

刷题专练之翻转题练习
文章目录一、 编写函数实现字符串翻转二、轮转数组总结一、 编写函数实现字符串翻转 描述 编写一个函数,实现字符串的翻转 输入描述: 输入一个字符串 输出描述: 输出翻转后的字符串 写法一: 这种方法是定义begin和end࿰…...

【Java】死锁
一、什么是死锁 死锁指多个线程在执行过程中,因争夺资源造成的一种相互等待的僵局。 进程死锁是指两个或两个以上的进程在执行过程中,由于竞争资源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推进下去。…...
迪杰斯特拉算法)
DS图—图的最短路径(无框架)迪杰斯特拉算法
目录 题目描述 AC代码 题目描述 给出一个图的邻接矩阵,输入顶点v,用迪杰斯特拉算法求顶点v到其它顶点的最短路径。 输入 第一行输入t,表示有t个测试实例 第二行输入顶点数n和n个顶点信息 第三行起,每行输入邻接矩阵的一行&…...
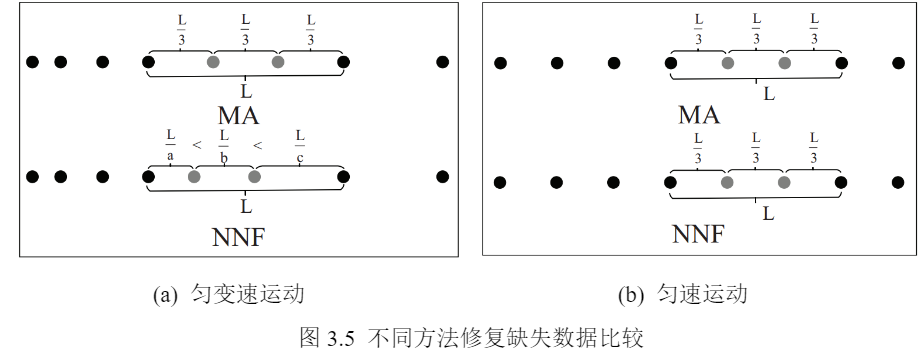
【笔记】数据异常检测与修复总结
文章目录一、异常种类1. 对于移动对象的数据异常2. 对于时序数据的异常检测二、异常数据清洗流程三、数据预处理四、异常检测算法五、异常修复算法六、漂移数据清洗一、异常种类 不同的研究对象,有着不同的异常分类方式 1. 对于移动对象的数据异常 异常数据信息&…...

算法笔记(七)—— 图的相关知识及算法
图的存储方式 1. 邻接表(记录关于某点的直接相邻点) 2. 邻接矩阵(一定是正方形的矩阵,对点进行编号,点到点的权值由距震中的值表示,无直接相连记为正无穷) 图的模板 unordered_map<int,No…...

ssh配置互信时错误解决方法
之前项目中遇到有关配置ssh互信免密登录问题,为避免以后踩坑,现记录一下避坑指南。 1、提示如下错误: Permission denied (publickey,gssapi-keyex,gssapi-with-mic). 问题分析:可能是ssh配置问题。 查看日志/var/log/secure&…...

SQL69 返回产品并且按照价格排序
描述有Products 表prod_idprod_nameprod_pricea0011egg3a0019sockets4b0019coffee15【问题】编写 SQL 语句,返回 Products 表中所有价格在 3 美元到 6 美元之间的产品的名称(prod_name)和价格(prod_price),…...

vue+elementUI 实现设置还款日字母弹窗组件
1、业务背景 还款业务,设置每月还款日,选每月几号扣款,不需要29、30、31,因为不是每个月都有这三天的 2、预期效果图 3、代码实现 3.1 初始化vue项目 地址:https://cn.vuejs.org/guide/introduction.html 3.2 在项…...
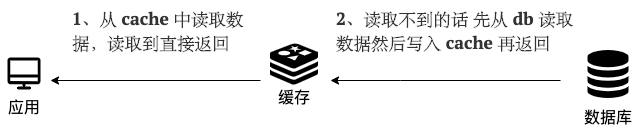
【JavaGuide面试总结】Redis篇·中
【JavaGuide面试总结】Redis篇中1.Redis 单线程模型了解吗?2.Redis6.0 之后为何引入了多线程?3.Redis 是如何判断数据是否过期的呢?4.过期的数据的删除策略了解么?5.Redis 内存淘汰机制了解么?6.什么是 RDB 持久化&…...
)
Python:每日一题之全球变暖(BFS连通性判断)
题目描述 你有一张某海域 NxN 像素的照片,"."表示海洋、"#"表示陆地,如下所示: ....... .##.... .##.... ....##. ..####. ...###. ....... 其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿…...
VUE -- defineExpose
defineExpose定义demo定义 defineExpose定义:用于组件通信中父级组件调用操作子组建方法和响应式属性参数能力 在使用definExpose前需要了解两个拷贝对象函数 对象copy:shallowReactive 与 数据 copy:shallowRef 这两个都是vue包里面的 简…...

实用调试技巧【下篇】
🔴本文章是在 Visual Studio 2022(VS2022)编译环境下进行操作讲解 文章目录3.2.调试的时候查看程序当前信息3.2.1.查看临时变量的值3.2.2.查看内存信息3.2.3.查看调用堆栈3.2.4.查看汇编信息🥳4.调试实例🥳5.如何写出&…...

【数据结构期末例题】
前言 本文是博主自己在准备学校数据结构考试时的总结,各个知识点都贴有对应的详细讲解文章以供大家参考;当然文中还有许许多多的截图,这些是博主对主要内容的摘取,对于那些基础较好的同学可以直接看截图,减少跳转对应文…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
