数值分析第七章节 用Python实现非线性方程与方程组的数值解法
参考书籍:数值分析 第五版 李庆杨 王能超 易大义编 第7章 非线性方程与方程组的数值解法
文章声明:如有发现错误,欢迎批评指正
文章目录
7.1方程求根与二分法:太简单了(程序设计竞赛这些都是基本)。直接跳过。注意一下一些概念。
7.2不动点迭代法及其收敛性:7.2.1不动点与不动点迭代法: f ( x ) = 0 f(x)=0 f(x)=0恒等变为 x = φ ( x ) x=\varphi(x) x=φ(x)。用迭代方程 x k + 1 = φ ( x k ) x_{k+1}=\varphi(x_k) xk+1=φ(xk), x ( 0 ) x_{(0)} x(0)随便选。如 lim k → ∞ x k = x ∗ \lim\limits_{k\rightarrow\infty}x_k=x^* k→∞limxk=x∗,则称迭代方程收敛;反之,发散。7.2.2不动点的存在性与迭代法的收敛性:定理1 设 φ ( x ) ∈ C [ a , b ] \varphi(x)\in C[a,b] φ(x)∈C[a,b]满足以下两个条件:(1)对任意的 x ∈ [ a , b ] x\in[a,b] x∈[a,b]有 a ≤ φ ( x ) ≤ b a\leq\varphi(x)\leq b a≤φ(x)≤b(2)存在正常数 L < 1 L<1 L<1,使对任意 x , y ∈ [ a , b ] x,y\in[a,b] x,y∈[a,b]都有 ∣ φ ( x ) − φ ( y ) ∣ ≤ L ∣ x − y ∣ |\varphi(x)-\varphi(y)|\leq L|x-y| ∣φ(x)−φ(y)∣≤L∣x−y∣,则 φ ( x ) \varphi(x) φ(x)在 [ a , b ] [a,b] [a,b]上存在唯一的不动点 x ∗ x^* x∗。证明可以看下,不是特别困难。7.2.3局部收敛性与收敛阶:不作讨论。
迭代法求解 x e x − 1 = 0 xe^x-1=0 xex−1=0
from math import e
x=0.5
print(f"k={0:02d},{x:.10f}")
for i in range(10):x=1/pow(e,x)print(f"k={i+1:02d},{x:.10f}")

7.3迭代收敛的加速方法:不作讨论
7.4牛顿法:7.4.1牛顿法及其收敛性:牛顿法 x k + 1 = x k − f ( x k ) f ′ ( x k ) , k = 0 , 1 , … , x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)},k=0,1,\dots, xk+1=xk−f′(xk)f(xk),k=0,1,…,(又切线法)
7.4.2牛顿法的应用举例:不作讨论。7.4.3简化牛顿法与牛顿下山法。牛顿法的优点是收敛快,缺点是每步迭代要计算 f ( x k ) f(x_k) f(xk)及 f ′ ( x k ) f'(x_k) f′(xk),计算量较大且有时 f ′ ( x k ) f'(x_k) f′(xk)计算较困难;二是初始近似 x 0 x_0 x0只在根 x ∗ x^* x∗附近才能保证收敛,如 x 0 x_0 x0给的不合适可能不收敛。为克服这两个缺点,通常可用下述方法。简化牛顿法 x k + 1 = x k − 1 f ′ ( x 0 ) f ( x k ) x_{k+1}=x_k-\frac{1}{f'(x_0)}f(x_k) xk+1=xk−f′(x0)1f(xk);牛顿下山法 x k + 1 = x k − λ f ( x k ) x_{k+1}=x_k-\lambda f(x_k) xk+1=xk−λf(xk)。 λ \lambda λ为下山因子,从1开取,逐次减半,直到满足条件 ∣ f ( x k + 1 ) ∣ < ∣ f ( x k ) ∣ |f(x_{k+1})|<|f(x_k)| ∣f(xk+1)∣<∣f(xk)∣止。
牛顿法求解 x e x − 1 = 0 xe^x-1=0 xex−1=0
from math import e
def func(x):return x-(x*pow(e,x)-1)/(pow(e,x)*(1+x))
x=0.5
print(f"k={0:02d},{x:.10f}")
for i in range(10):x=func(x)print(f"k={i+1:02d},{x:.10f}")

简化牛顿法求解 x e x − 1 = 0 xe^x-1=0 xex−1=0
from math import e
def func(x):return x*pow(e,x)-1
x=0.5
print(f"k={0:02d},{x:.10f}")
C=1/(pow(e,x)*(1+x))
for i in range(10):x=x-C*func(x)print(f"k={i+1:02d},{x:.10f}")

算了,开摆。就这样吧,不想写了。
相关文章:

数值分析第七章节 用Python实现非线性方程与方程组的数值解法
参考书籍:数值分析 第五版 李庆杨 王能超 易大义编 第7章 非线性方程与方程组的数值解法 文章声明:如有发现错误,欢迎批评指正 文章目录 迭代法求解 x e x − 1 0 xe^x-10 xex−10牛顿法求解 x e x − 1 0 xe^x-10 xex−10简化牛顿法求解 …...
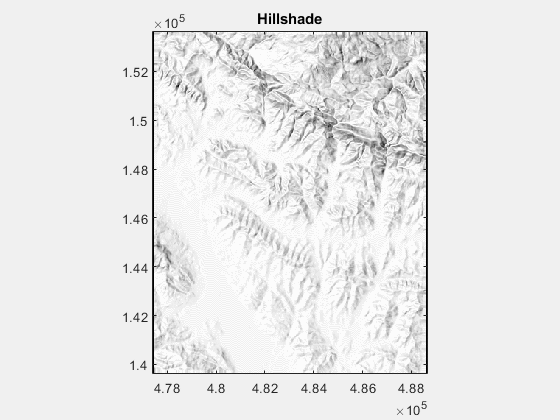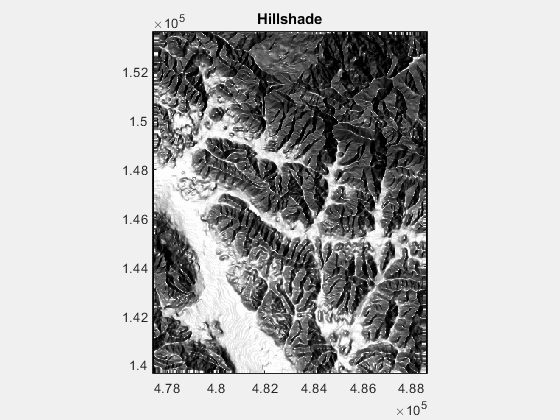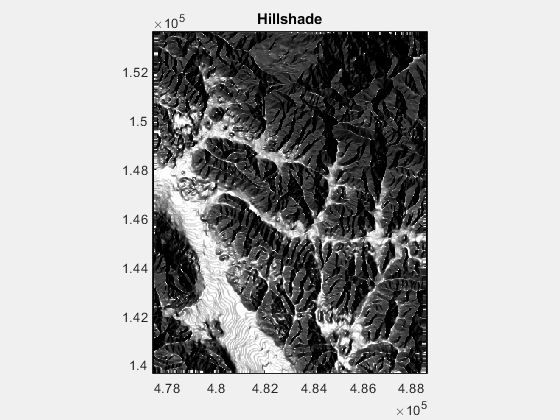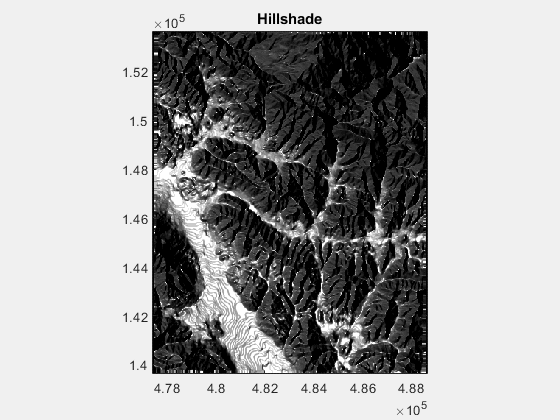
利用MATLAB制作DEM山体阴影
在地理绘图中,我们使用的DEM数据添加山体阴影使得绘制的图件显得更加的美观。 GIS中使用ArcGIS软件就可以达到这一目的,或者使用GMT,同样可以得到山体阴影的效果。 本文提供了一个MATLAB的函数,可以得到山体阴影。 clear all;c…...

ubuntu 使用 rsync 的 SSH 方式同步备份远程WEB服务器
ubuntu 20.04 自带 rsync ,对于 WEB 服务器这种更新频率不高的情况,直接使用定时同步复制远程服务器的方法,比较直接和简单! $ rsync --version rsync version 3.1.3 protocol version 31 参考: Ubuntu20.04中的rsyn…...
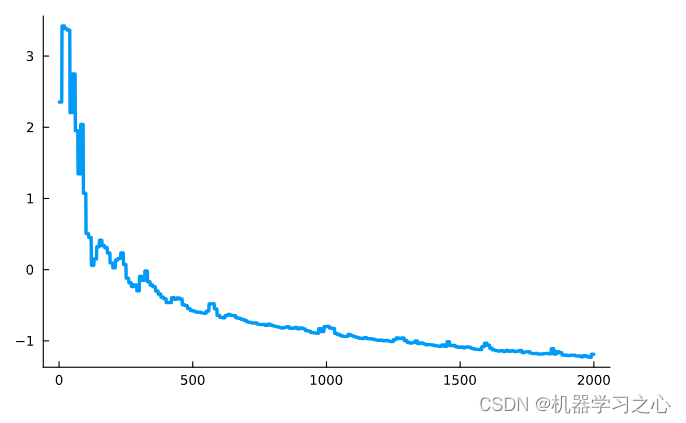
机器学习 | Python实现NARX模型预测控制
机器学习 | Python实现NARX模型预测控制 目录 机器学习 | Python实现NARX模型预测控制效果一览基本介绍研究内容程序设计参考资料效果一览 基本介绍 机器学习 | Python实现NARX模型预测控制 研究内容 贝叶斯黑盒模型预测控制,基于具有外源输入的非线性自回归模型的预期自由能最…...
M5ATOMS3基础03给ROS1发一个问候(rosserial)
引出问题 关于之前2020年的博客: 01. ESP8266和ROS调试一些问题汇总 02. ESP8266和ESP32配置(需使用ROS1和ROS2) 效果展示 使用M5ATOMS3与ROS1(kinetic,melodic,noetic)版本通信比较通用的是…...
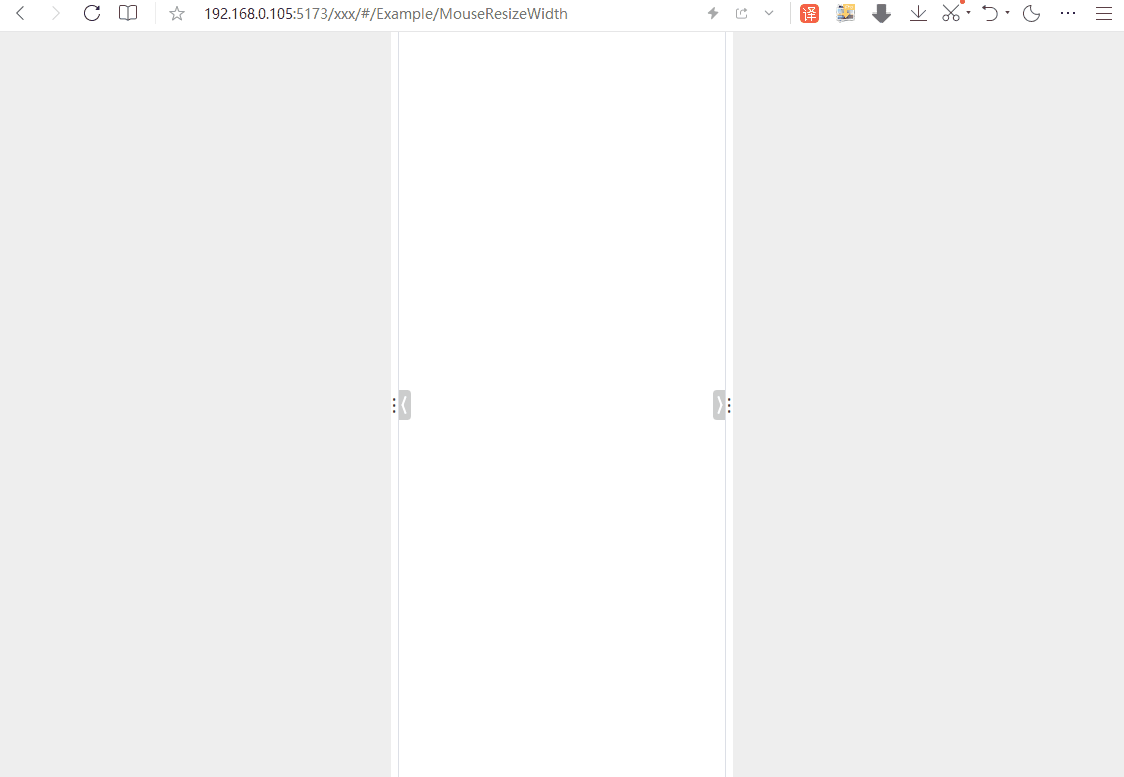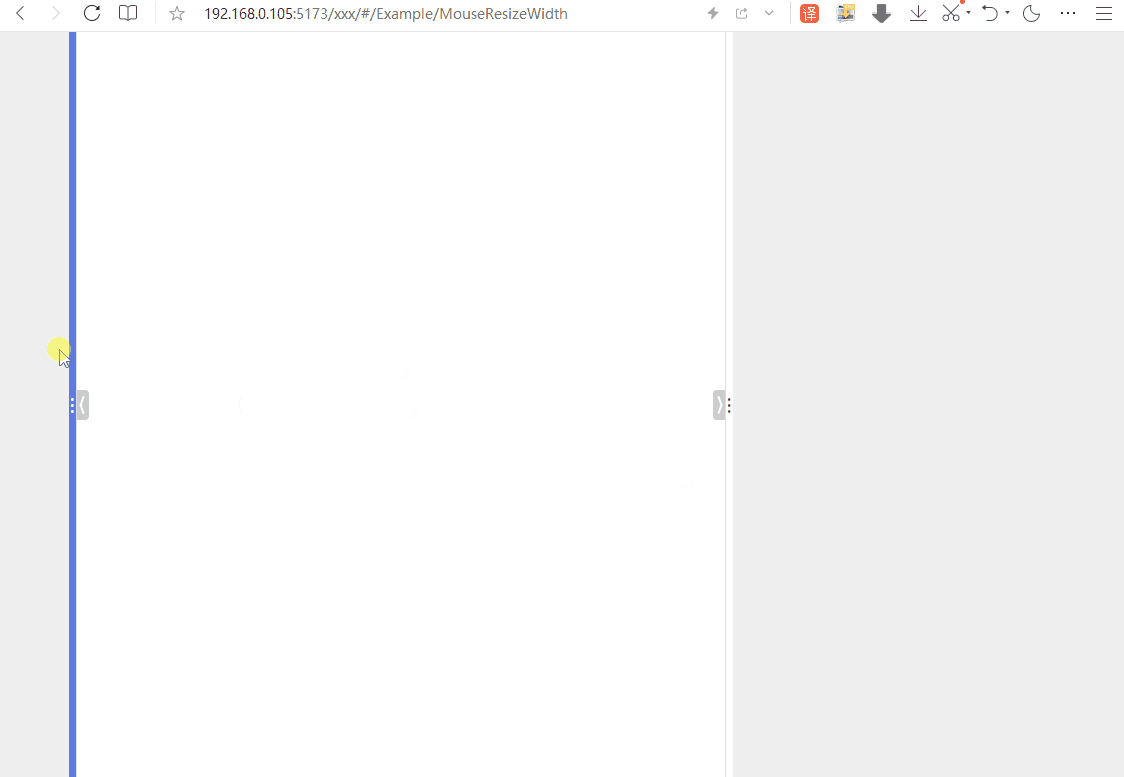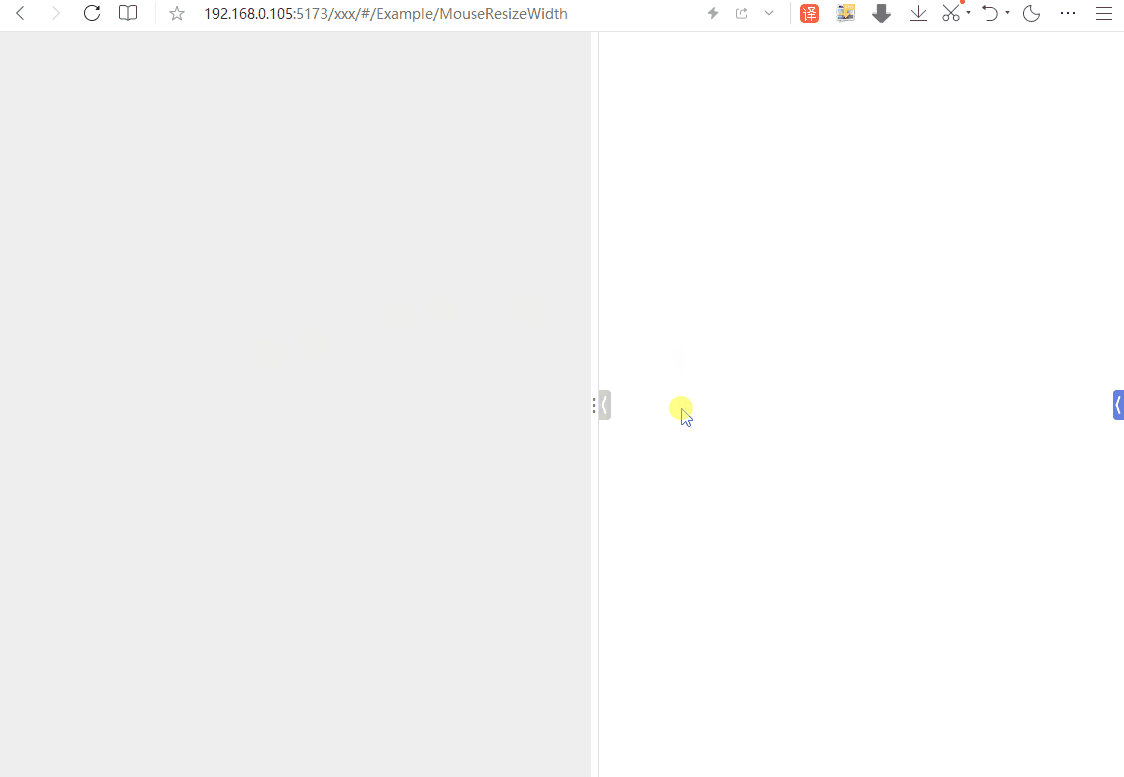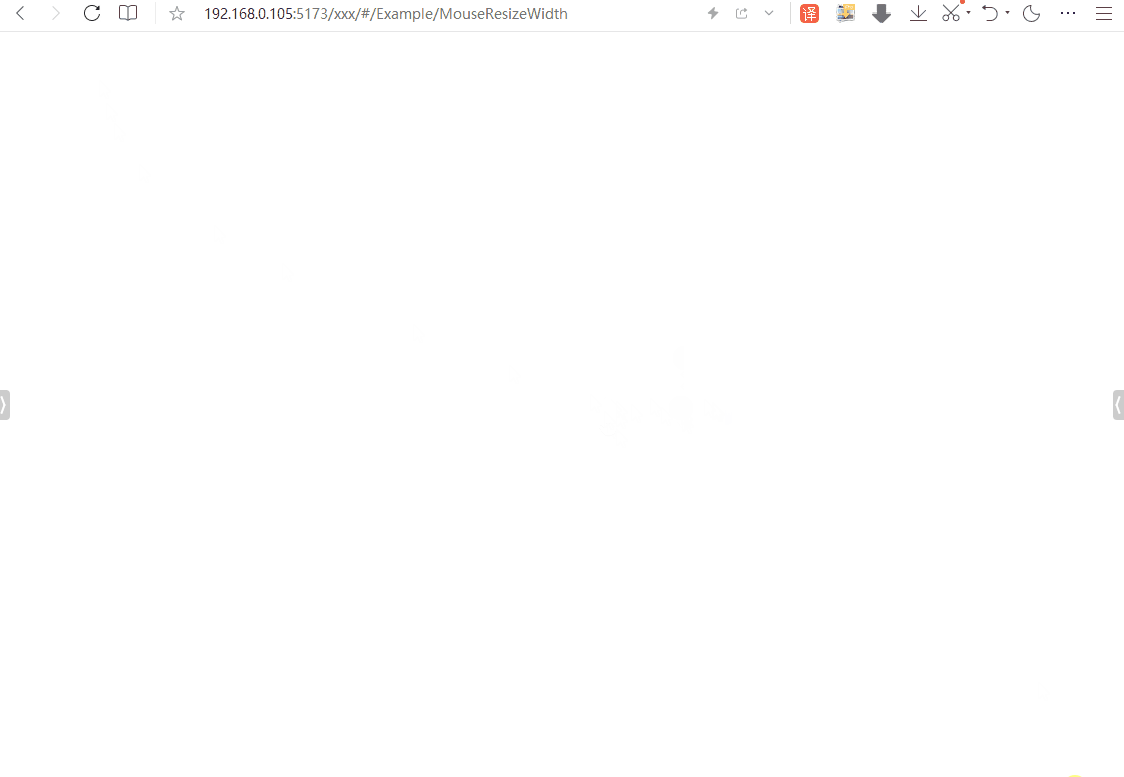
基于Vue3实现鼠标按下某个元素进行移动,实时改变左侧或右侧元素的宽度,以及点击收起或展开的功能
其原理主要是利用JavaScript中的鼠标事件来控制CSS样式。大致就是监听某个DOM元素的鼠标按下事件,以及按下之后的移动事件和松开事件。在鼠标按下且移动过程中,可实时获得鼠标的X轴坐标的值,通过简单计算,可计算出目标元素的宽度&…...
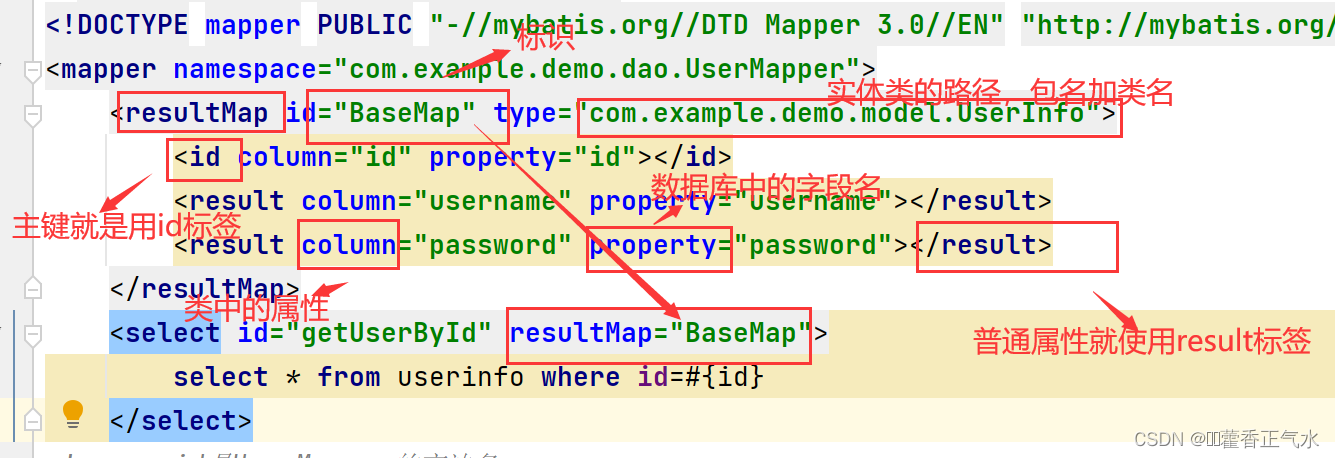
使用MyBatis(2)
目录 一、定义接口、实体类、创建XML文件实现接口) 二、MyBatis的增删改查 🍅1、MyBatis传递参数查询 🎈写法一 🎈写法二 🎈两种方式的区别 🍅2、删除操作 🍅3、根据id修改用户名 &#x…...

【FPGA/D6】
2023年7月25日 VGA控制器 视频23notecodetb 条件编译error时序图保存与读取??RGBTFT显示屏 视频24PPI未分配的引脚或电平的解决方法 VGA控制器 视频23 note MCU单片机 VGA显示实时采集图像 行消隐/行同步/场同步/场消隐 CRT:阴极射线管 640…...

【WebGIS实例】(10)Cesium开场效果(场景、相机旋转,自定义图片底图)
效果 漫游效果视频: 【WebGIS实例】(10)Cesium开场效果(场景、相机 点击鼠标后将停止旋转并正常加载影像底图: 代码 可以直接看代码,注释写得应该比较清楚了: /** Date: 2023-07-28 16:21…...
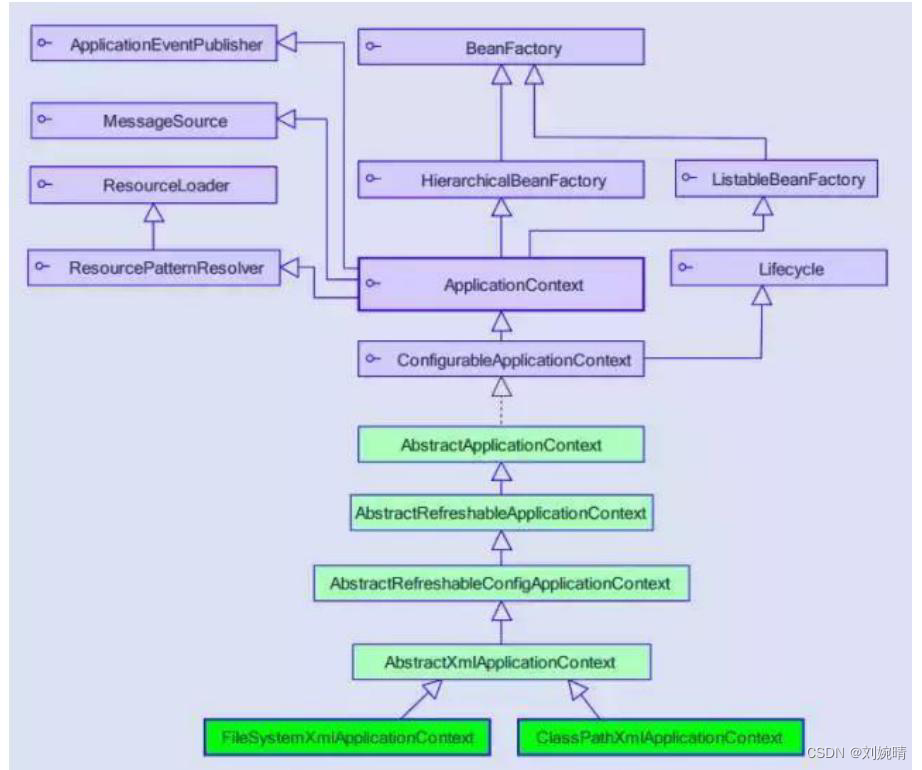
【Spring】IOC的原理
一、 IOC 的概念 Spring 的 IOC ,即控制反转,所谓控制反转 —— 本来管理业务对象(bean)的操作是由我们程序员去做的,但是有了 Spring 核心容器后,这些 Bean 对象的创建和管理交给我们Spring容器去做了&am…...
AI加速游戏开发 亚马逊云科技适配3大场景,打造下一代游戏体验
随着疫情的消散,中国游戏产业正在快速前进。在伴随着游戏产业升级的同时,整个行业都在面临着新的挑战与新的诉求。亚马逊云科技游戏研发解决方案和服务,覆盖端到端3大场景,为游戏公司与游戏开发人员赋能。 场景1:AI辅助…...
,(派生类,子类))
C++ | 继承(基类,父类,超类),(派生类,子类)
文章参考:https://blog.csdn.net/war1111886/article/details/8609957 一 .继承中的访问权限关系 1.基类,父类,超类是指被继承的类,派生类,子类是指继承于基类的类. 2…...

Commands Of Hadoop
序言 持续整理下常用的命令cuiyaonan2000163.com Command 文件拷贝 当从多个源拷贝时,如果两个源冲突,distcp会停止拷贝并提示出错信息,. 如果在目的位置发生冲突,会根据选项设置解决。 默认情况会跳过已经存在的目标文件&am…...

SQL-每日一题【620.有趣的电影】
题目 某城市开了一家新的电影院,吸引了很多人过来看电影。该电影院特别注意用户体验,专门有个 LED显示板做电影推荐,上面公布着影评和相关电影描述。 作为该电影院的信息部主管,您需要编写一个 SQL查询,找出所有影片…...

linux 精华总结
...

Eureka 学习笔记2:客户端 DiscoveryClient
版本 awsVersion ‘1.11.277’ DiscoveryClient # cacheRefreshTask // 配置shouldFetchRegistry if (clientConfig.shouldFetchRegistry()) {// 配置client.refresh.intervalint registryFetchIntervalSeconds clientConfig.getRegistryFetchIntervalSeconds();// 配置expB…...
okhttp原理分析
工程目录图 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 01okhttp module里 包含的设计模式:建造者设计模式、责任链设计模式 CustomInject 演示自定义注解 代码:okhttp原理分析、Andro…...

freeswitch的mod_xml_curl模块
概述 freeswitch是一款简单好用的VOIP开源软交换平台。 随着fs服务的增多,每一台fs都需要在后台单独配置,耗时耗力,心力憔悴。 如果有一个集中管理配置的配置中心,统一管理所有fs的配置,并可以实现动态的修改配置就…...

高速数据采集专家-FMC140【产品手册】
FMC140是一款具有缓冲模拟输入的低功耗、12位、双通道(5.2GSPS/通道)、单通道10.4GSPS、射频采样ADC模块,该板卡为FMC标准,符合VITA57.1规范,该模块可以作为一个理想的IO单元耦合至FPGA前端,8通道的JESD204…...

【SSM】知识集锦
项目一:狂神JAVA 功能1:实现全部书籍查询 1.思路:首页index.jsp ——>Controller——>hello.jsp 2.步骤: step1:index.jsp <% page language"java" contentType"text/html; charsetUTF-8" page…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
