#P0999. [NOIP2008普及组] 排座椅
题目描述
上课的时候总会有一些同学和前后左右的人交头接耳,这是令小学班主任十分头疼的一件事情。不过,班主任小雪发现了一些有趣的现象,当同学们的座次确定下来之后,只有有限的 DD 对同学上课时会交头接耳。
同学们在教室中坐成了 MM 行 NN 列,坐在第 ii 行第 jj 列的同学的位置是 (i,j)(i,j),为了方便同学们进出,在教室中设置了 KK 条横向的通道,LL 条纵向的通道。
于是,聪明的小雪想到了一个办法,或许可以减少上课时学生交头接耳的问题:她打算重新摆放桌椅,改变同学们桌椅间通道的位置,因为如果一条通道隔开了 22 个会交头接耳的同学,那么他们就不会交头接耳了。
请你帮忙给小雪编写一个程序,给出最好的通道划分方案。在该方案下,上课时交头接耳的学生的对数最少。
输入格式
第一行,有 55 个用空格隔开的整数,分别是 M,N,K,L,D(2 \le N,M \le 1000,0 \le K<M,0 \le L<N,D \le 2000)M,N,K,L,D(2≤N,M≤1000,0≤K<M,0≤L<N,D≤2000)。
接下来的 DD 行,每行有 44 个用空格隔开的整数。第 ii 行的 44 个整数 X_i,Y_i,P_i,Q_iXi,Yi,Pi,Qi,表示坐在位置 (X_i,Y_i)(Xi,Yi) 与 (P_i,Q_i)(Pi,Qi) 的两个同学会交头接耳(输入保证他们前后相邻或者左右相邻)。
输入数据保证最优方案的唯一性。
输出格式
共两行。 第一行包含 KK 个整数 a_1,a_2,\ldots,a_Ka1,a2,…,aK,表示第 a_1a1 行和 a_1+1a1+1 行之间、第 a_2a2 行和 a_2+1a2+1 行之间、…、第 a_KaK 行和第 a_K+1aK+1 行之间要开辟通道,其中 a_i< a_{i+1}ai<ai+1,每两个整数之间用空格隔开(行尾没有空格)。
第二行包含 LL 个整数 b_1,b_2,\ldots,b_Lb1,b2,…,bL,表示第 b_1b1 列和 b_1+1b1+1 列之间、第 b_2b2 列和 b_2+1b2+1 列之间、…、第 b_LbL 列和第 b_L+1bL+1 列之间要开辟通道,其中b_i< b_{i+1}bi<bi+1,每两个整数之间用空格隔开(列尾没有空格)。
输入数据 1
4 5 1 2 3
4 2 4 3
2 3 3 3
2 5 2 4
Copy
输出数据 1
2
2 4
Copy
提示
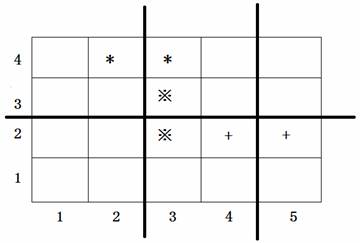
上图中用符号*、※、+标出了 33 对会交头接耳的学生的位置,图中 33 条粗线的位置表示通道,图示的通道划分方案是唯一的最佳方案。
NOIP 2008 普及组 第二题
代码:
#include <stdio.h>
#include <stdlib.h>int min(int a, int b);int main()
{int m = 0, n = 0, k = 0, l = 0, d = 0;int x[1010] = {0}, y[1010] = {0};int col[1010] = {0}, row[1010] = {0};scanf("%d%d%d%d%d", &m, &n, &k, &l, &d);for (int i = 1; i <= d; i++){int x1, y1, x2, y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);if (x1 != x2) //判断x是否相等{ //不等时一定存在y有相同//取最小加一最大减一y[min(x1, x2)]++; //价值}else{ //等于x[min(y1, y2)]++;}}for (int i = 1; i <= k; i++){
//对y进行价值排序int max = -1;int index = 0;for (int j = 1; j < m; j++){if (y[j] > max){max = y[j];index = j;}}y[index] = 0;col[index]++;}for (int i = 1; i <= l; i++){//对y进行价值排序int max = -1;int index = 0;for (int j = 1; j < n; j++){if (x[j] > max){max = x[j];index = j;}}x[index] = 0;row[index]++;}for (int i = 0; i < 1010; i++){if (col[i])//遍历x{printf("%d ", i);}}printf("\n");for (int i = 0; i< 1010;i++){if (row[i]){printf("%d ", i);}}return 0;
}int min(int a, int b)
{return a < b ? a : b;
}
相关文章:

#P0999. [NOIP2008普及组] 排座椅
题目描述 上课的时候总会有一些同学和前后左右的人交头接耳,这是令小学班主任十分头疼的一件事情。不过,班主任小雪发现了一些有趣的现象,当同学们的座次确定下来之后,只有有限的 DD 对同学上课时会交头接耳。 同学们在教室中坐…...

Sentinel 容灾中心的使用
Sentinel 容灾中心的使用 往期文章 Nacos环境搭建Nacos注册中心的使用Nacos配置中心的使用 熔断/限流结果 Jar 生产者 spring-cloud-alibaba:2021.0.4.0 spring-boot:2.6.8 spring-cloud-loadbalancer:3.1.3 sentinel:2021.0…...

深度学习中简易FC和CNN搭建
TensorFlow是由谷歌开发的PyTorch是由Facebook人工智能研究院(Facebook AI Research)开发的 Torch和cuda版本的对应,手动安装较好 全连接FC(Batch*Num) 搭建建议网络: from torch import nnclass Mnist_NN(nn.Module):def __i…...

【多模态】20、OVR-CNN | 使用 caption 来实现开放词汇目标检测
文章目录 一、背景二、方法2.1 学习 视觉-语义 空间2.2 学习开放词汇目标检测 三、效果 论文:Open-Vocabulary Object Detection Using Captions 代码:https://github.com/alirezazareian/ovr-cnn 出处:CVPR2021 Oral 一、背景 目标检测数…...
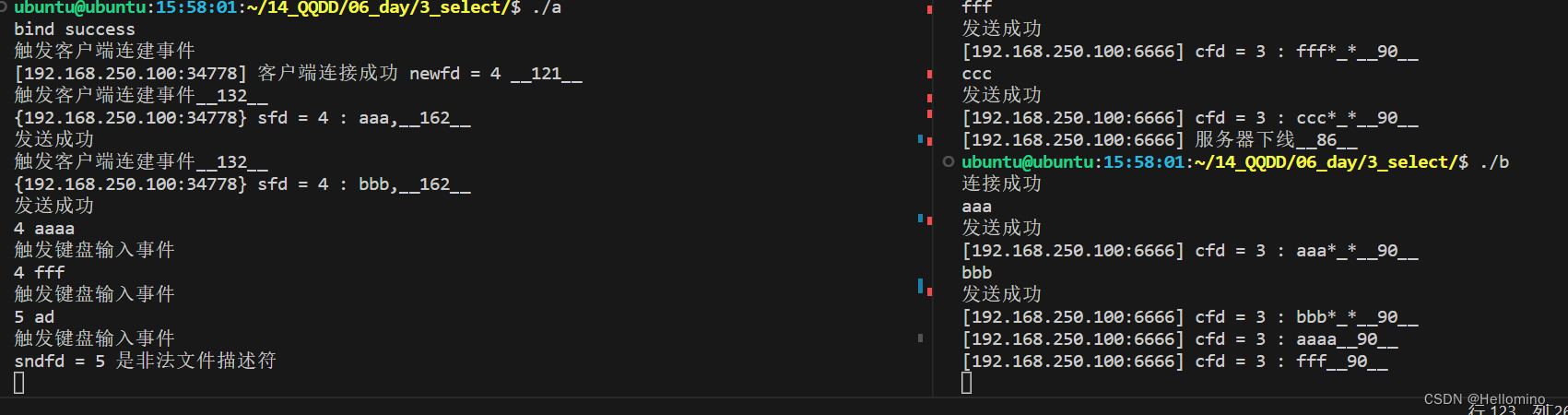
网络编程 IO多路复用 [select版] (TCP网络聊天室)
//head.h 头文件 //TcpGrpSer.c 服务器端 //TcpGrpUsr.c 客户端 select函数 功能:阻塞函数,让内核去监测集合中的文件描述符是否准备就绪,若准备就绪则解除阻塞。 原型: #include <sys/select.…...

数学建模学习(7):单目标和多目标规划
优化问题描述 优化 优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值 线性规划 线性规划是指目标函数和约束都是线性的情况 [x,fval]linprog(f,A,b,Aeq,Beq,LB,U…...

Element UI如何自定义样式
简介 Element UI是一套非常完善的前端组件库,但是如何个性化定制其中的组件样式呢?今天我们就来聊一聊这个 举例 就拿最常见的按钮el-button来举例,一般来说默认是蓝底白字。效果图如下 可是我们想个性化定制,让他成为粉底红字应…...

protobuf入门实践2
如何在proto中定义一个rpc服务? syntax "proto3"; //声明protobuf的版本package fixbug; //声明了代码所在的包 (对于C来说就是namespace)//下面的选项,表示生成service服务类和rpc方法描述, 默认是不生成的 option cc_generi…...

adb shell使用总结
文章目录 日志记录系统概览adb 使用方式 adb命令日志过滤按照告警等级进行过滤按照tag进行过滤根据告警等级和tag进行联合过滤屏蔽系统和其他App干扰,仅仅关注App自身日志 查看“当前页面”Activity文件传输截屏和录屏安装、卸载App启动activity其他 日志记录系统概…...
-Tag的含义、Tag类型与其他的转换)
UG NX二次开发(C++)-Tag的含义、Tag类型与其他的转换
文章目录 1、前言2、Tag号的含义3、tag_t转换为int3、TaggedObject与Tag转换3.1 TaggedObject定义3.2 TaggedObject获取Tag3.3 根据Tag获取TaggedObject4.Tag与double类型的转换1、前言 在UG NX中,每个对象对应一个tag号,C++中,其类型是tag_t,一般是5位或者6位的int数字,…...
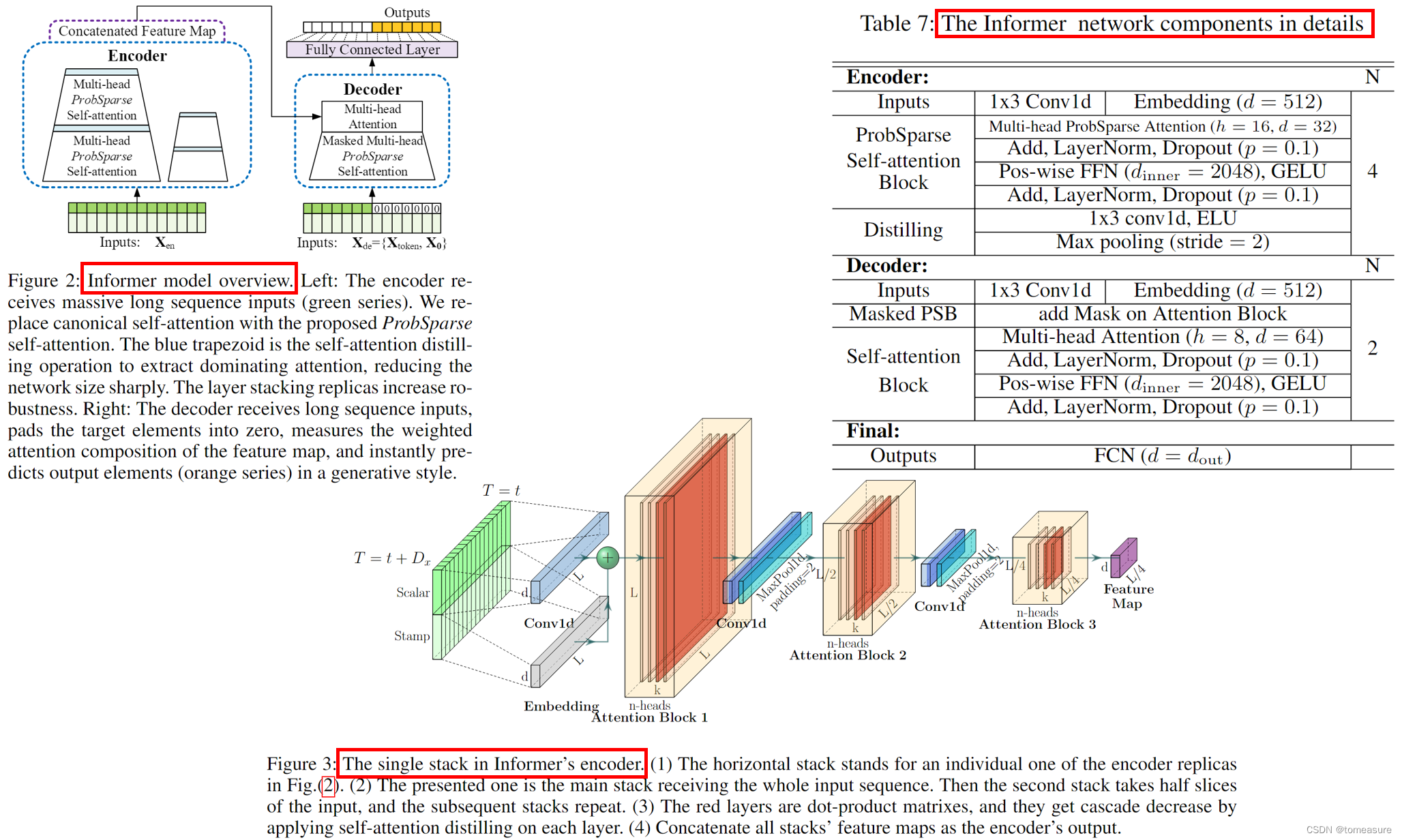
Informer 论文学习笔记
论文:《Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting》 代码:https://github.com/zhouhaoyi/Informer2020 地址:https://arxiv.org/abs/2012.07436v3 特点: 实现时间与空间复杂度为 O ( …...

c语言位段知识详解
本篇文章带来位段相关知识详细讲解! 如果您觉得文章不错,期待你的一键三连哦,你的鼓励是我创作的动力之源,让我们一起加油,一起奔跑,让我们顶峰相见!!! 目录 一.什么是…...
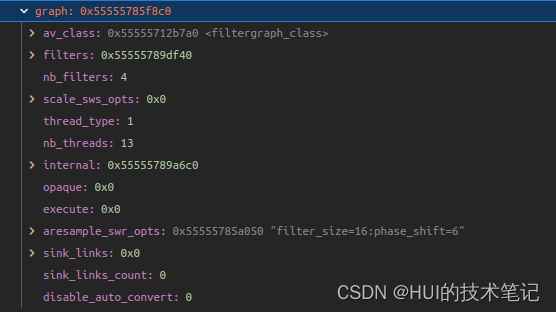
FFmpeg aresample_swr_opts的解析
ffmpeg option的解析 aresample_swr_opts是AVFilterGraph中的option。 static const AVOption filtergraph_options[] {{ "thread_type", "Allowed thread types", OFFSET(thread_type), AV_OPT_TYPE_FLAGS,{ .i64 AVFILTER_THREAD_SLICE }, 0, INT_MA…...

CAN学习笔记3:STM32 CAN控制器介绍
STM32 CAN控制器 1 概述 STM32 CAN控制器(bxCAN),支持CAN 2.0A 和 CAN 2.0B Active版本协议。CAN 2.0A 只能处理标准数据帧且扩展帧的内容会识别错误,而CAN 2.0B Active 可以处理标准数据帧和扩展数据帧。 2 bxCAN 特性 波特率…...

软工导论知识框架(二)结构化的需求分析
本章节涉及很多重要图表的制作,如ER图、数据流图、状态转换图、数据字典的书写等,对初学者来说比较生僻,本贴只介绍基础的轮廓,后面会有单独的帖子详解各图表如何绘制。 一.结构化的软件开发方法:结构化的分析、设计、…...

[SQL挖掘机] - 算术函数 - abs
介绍: 当谈到 SQL 中的 abs 函数时,它是一个用于计算数值的绝对值的函数。“abs” 代表 “absolute”(绝对),因此 abs 函数的作用是返回一个给定数值的非负值(即该数值的绝对值)。 abs 函数接受一个参数&a…...

vue拼接html点击事件不生效
vue使用ts,拼接html,点击事件不生效或者报 is not defined 点击事件要用onclick 不是click let data{name:测,id:123} let conHtml <div> "名称:" data.name "<br>" <p class"cursor blue&quo…...

【Spring】Spring之依赖注入源码解析
1 Spring注入方式 1.1 手动注入 xml中定义Bean,程序员手动给某个属性赋值。 set方式注入 <bean name"userService" class"com.firechou.service.UserService"><property name"orderService" ref"orderService"…...

【微软知识】微软相关技术知识分享
微软技术领域 一、微软操作系统: 微软的操作系统主要是 Windows 系列,包括 Windows 10、Windows Server 等。了解 Windows 操作系统的基本使用、配置和故障排除是非常重要的。微软操作系统(Microsoft System)是美国微软开发的Wi…...

12.python设计模式【观察者模式】
内容:定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变的时候,所有依赖于它的对象得到通知并被自动更新。观者者模式又称为“发布-订阅”模式。比如天气预报,气象局分发气象数据。 角色: 抽象主题…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
