SQL编译优化原理
最近在团队的OLAP引擎上做了一些SQL编译优化的工作,整理到了语雀上,也顺便发在博客上了。SQL编译优化理论并不复杂,只需要掌握一些关系代数的基础就比较好理解;比较困难的在于reorder算法部分。
文章目录
- 基础概念
- 关系代数等价
- join等价规则
- 基数
- join算法的成本
- 查询问题的分类
- 连接树的可能数量(搜索空间)
- 查询图、join树和问题复杂度
- Calcite概念
- cascade/volcano
- Calcite volcano递归优化器实现
- Join reorder
- 基于连接次序优化的动态规划算法
- IKKBZ算法
- bushy-tree
- ASI
- 归一化
- Calcite实践
- MultiJoinOptimizeBushyRule
- Join 算法选择
- 关联子查询优化
- 为什么要消除关联子查询?
- 基本消除规则
- project和filter去关联化
- Aggregate的去关联化
- 集合运算的去关联化
基础概念
关系代数等价
参考《数据库系统概念》第七版
下面是第六版
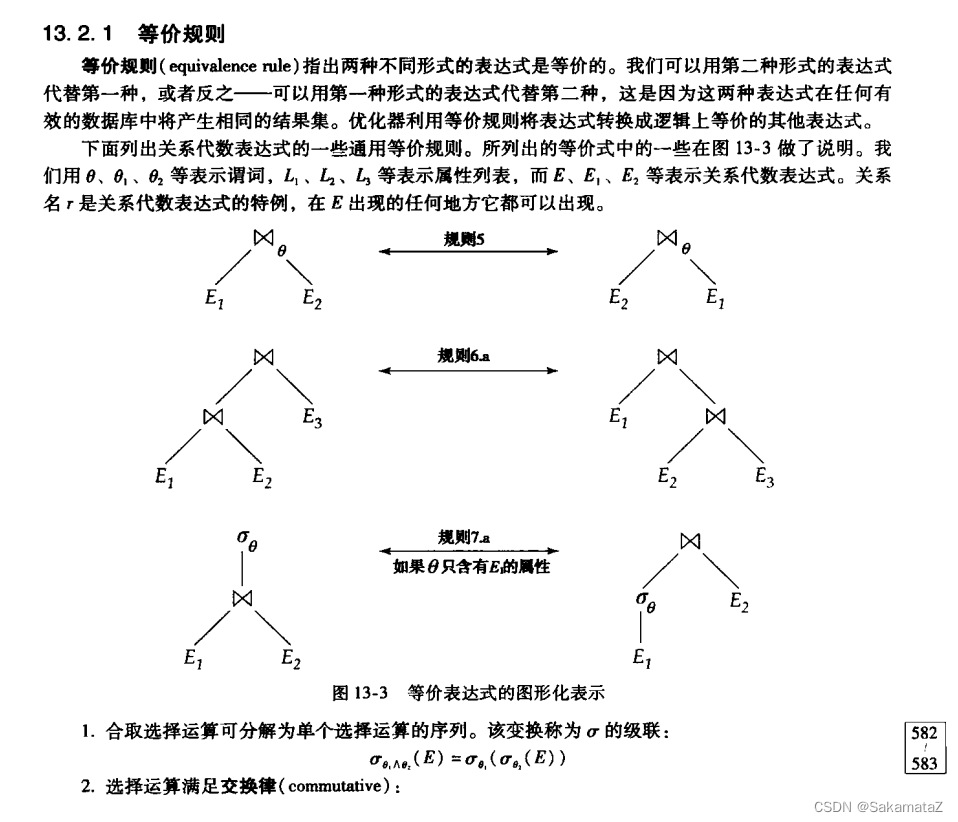

注意自然连接和θ连接的交换律不能用于外连接
join等价规则
https://www.comp.nus.edu.sg/~chancy/sigmod18-reorder.pdf
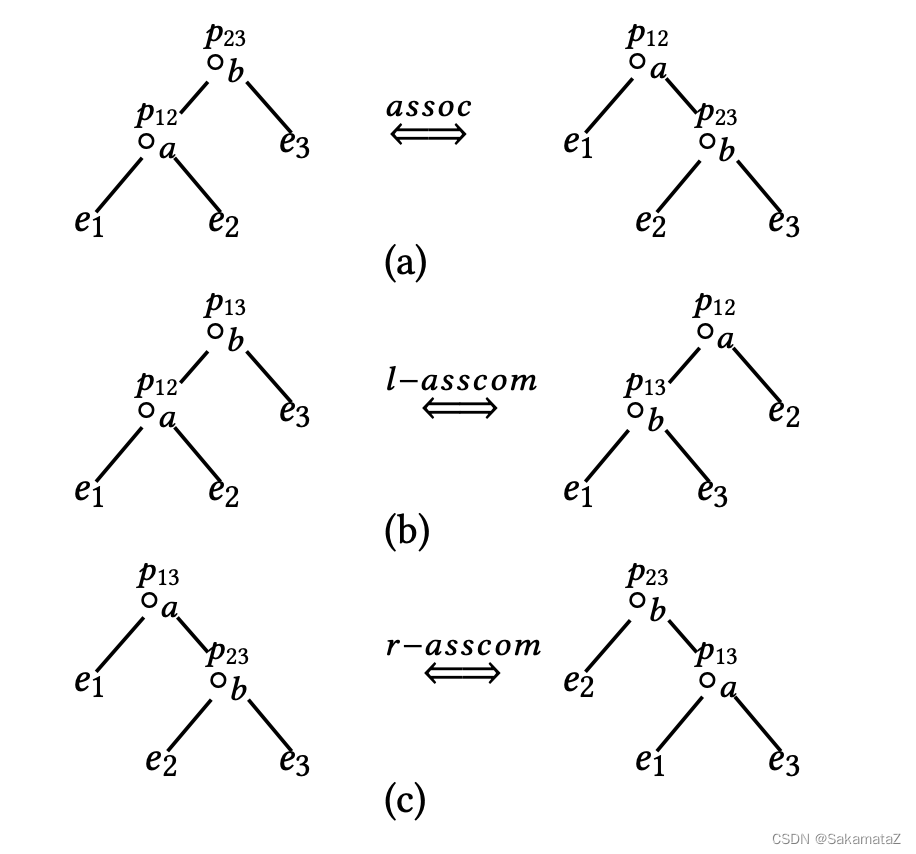
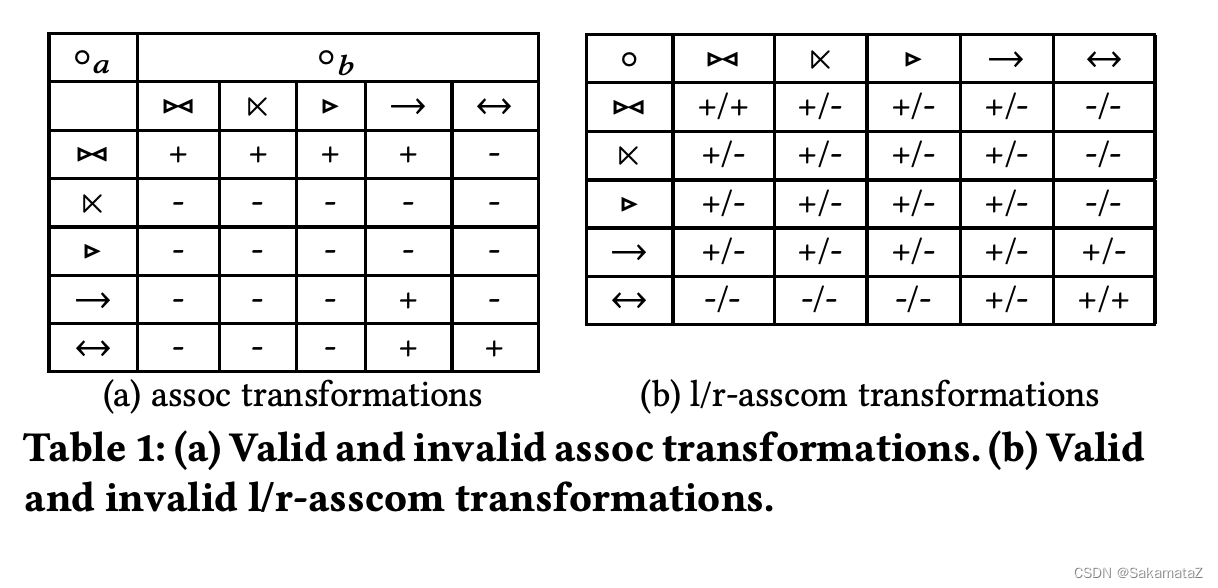
基数
基数(cardinality)表示不同值的数量
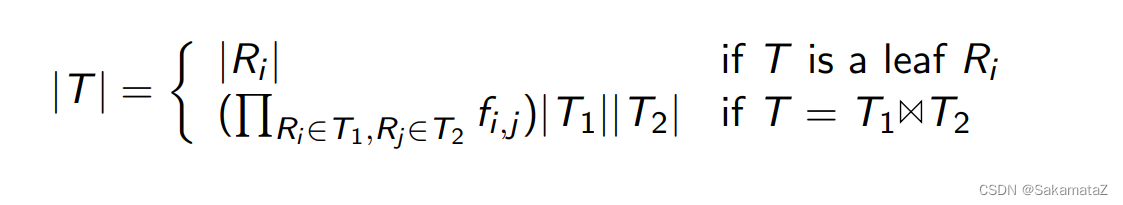
、
join算法的成本
从上到下依次为嵌套循环连接、hash连接、排序合并连接
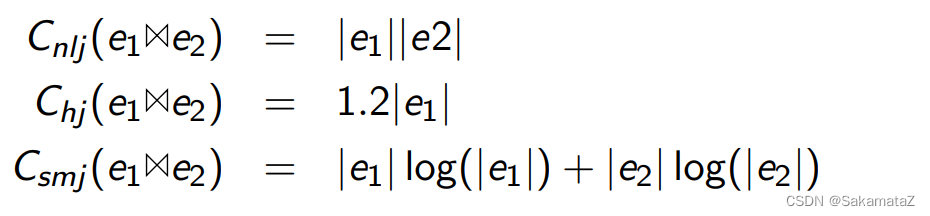
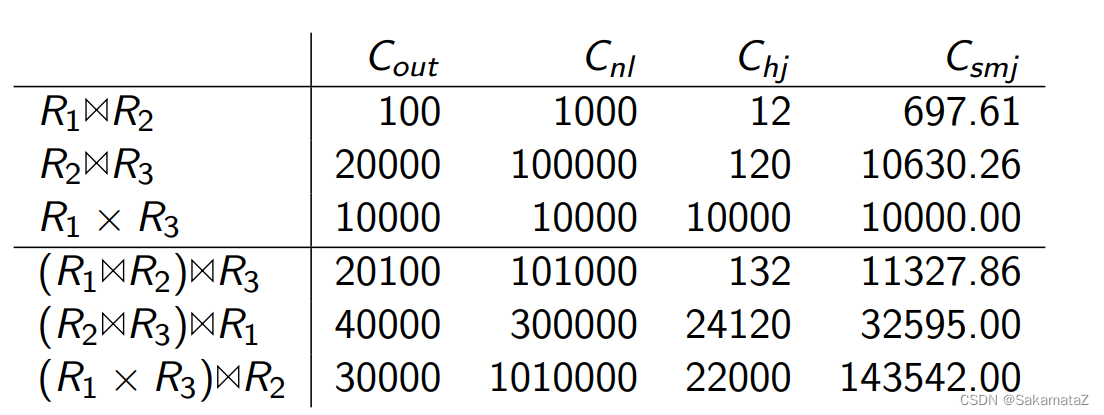

ASI(相邻序列交换)
查询问题的分类
按照查询图:chain、cycle、star、clique
按照查询树结构:left-deep、zig-zag、bushy tree
按照join结构:有没有cross product
按照成本函数:有没有ASI属性
连接树的可能数量(搜索空间)

查询图、join树和问题复杂度
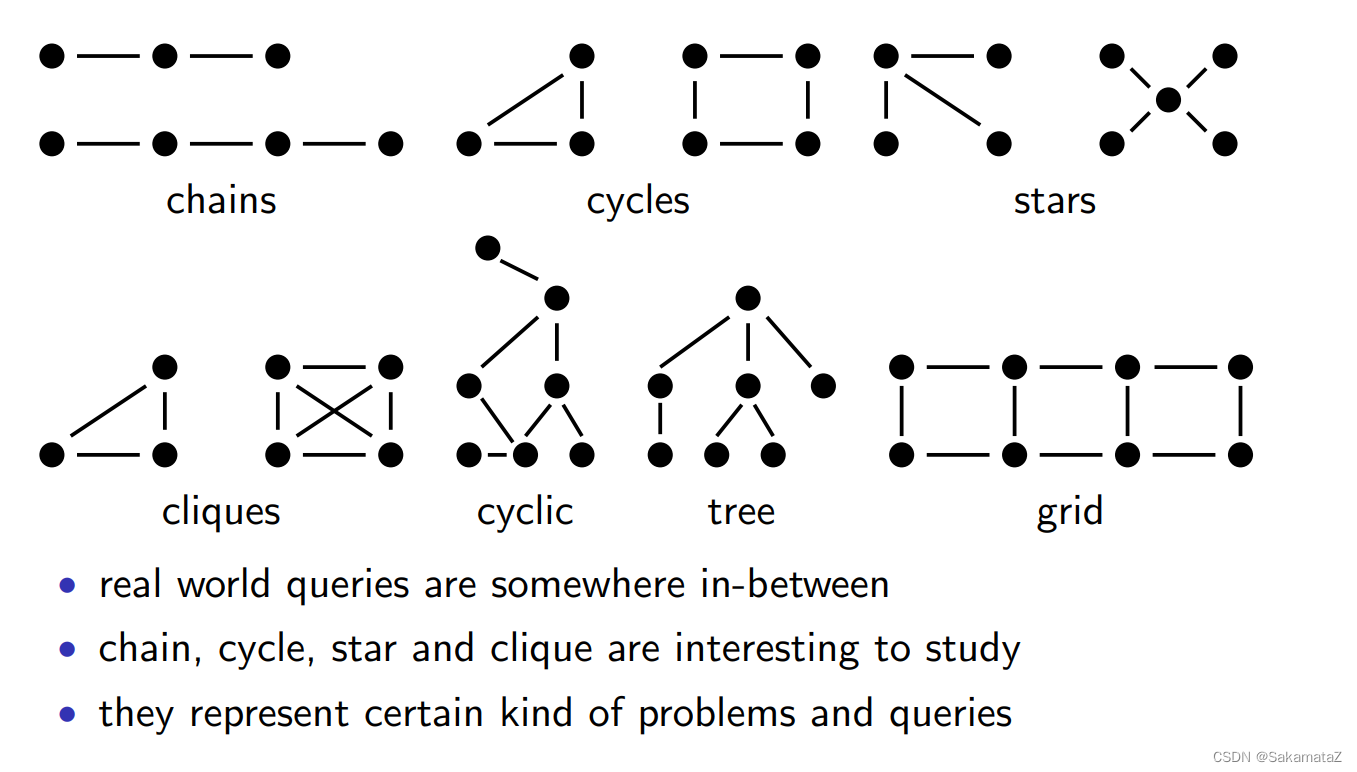
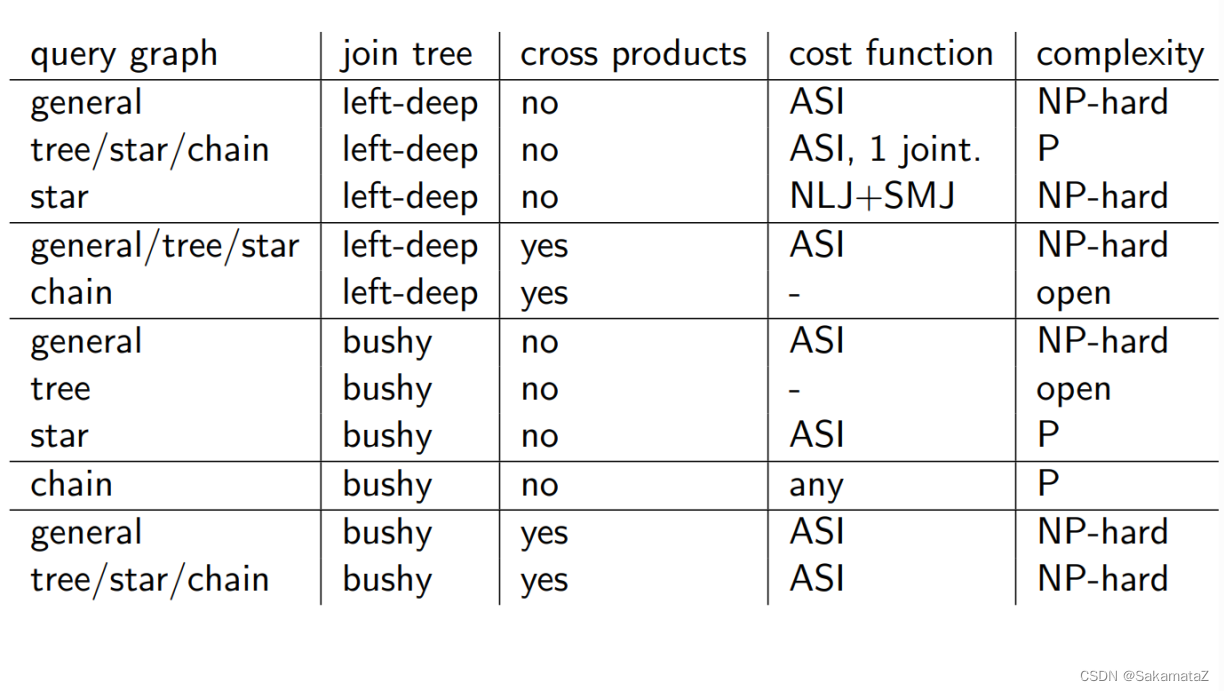
Calcite概念
RelNode:plan/subplan
relset:关系表达式等价的plan集合
relsubset :关系表达式和物理属性等价的plan集合
transformationRule:logical plan变化的规则集合
converterplan:将lp转化为pp的转化规则
RelOptRule :优化规则
RelOptNode 接口, 它代表的是能被 planner 操作的 expression node
statement:语句
reltrait 关系表达式特征
RelTraitDef 用于定义一类 RelTrait
RelTrait RelTrait是一个表示查询计划特征的抽象类。它用于描述查询计划的一些特性,是对应 TraitDef 的具体实例
Convention 是一种 RelTrait 用于表示 Rel 的调用约定(calling convention)
rexnode 行表达式
schema:逻辑模型
Program:一个SQL查询解析和优化的过程集合,可以将多个子过程组合在一起,以便进行SQL查询的解析和优化
cascade/volcano
volcano是top-down的模块化可剪枝sql优化模型。
volcano生成两个代数模型:logical and the physical algebras 分别优化lp和pp(pp主要选择执行算法)
一个volcano优化器必须提供如下部分:
(1) a set of logical operators,
(2) algebraic transformation rules, possibly with condition code,
(3) a set of algorithms and enforcers,
(4) implementation rules, possibly with condition code,
(5) an ADT “cost” with functions for basic arithmetic and comparison,
(6) an ADT “logical properties,”
(7) an ADT “physical property vector” including comparisons functions (equality and cover),
(8) an applicability function for each algorithm and enforcer,
(9) a cost function for each algorithm and enforcer,
(10) a property function for each operator, algorithm, and enf
volcano使用backward chaining的方式,只探索实际参与更大表达式的子查询和计划。这种方法可以避免对无关的子查询和计划进行搜索,从而提高查询优化的效率。
Calcite volcano递归优化器实现
RuleQueue 是一个优先队列,包含当前所有可行的 RuleMatch,findBestExpr() 时每次循环中我们从中取出优先级最高的并 apply,再根据 apply 的结果更新队列……如此往复,直到满足终止条件。
RuleQueue并没有使用大顶堆,仅仅保存了importance最大的节点。
我们想象我们现在有一组relnode,匹配上了很多RuleMatch,怎么决定先进行哪个match呢?
RuleMatch的importance决定了先进行哪个match,rulematch的importance定义为以下两个中较大的一个:
- 输入的 RelSubset 的 importance
- 输出的 RelSubset 的 importance
RelSubset的importance又该如何定义?importance 定义为以下两个中比较大的一个:
● 该 RelSubset 本身的真实 importance
● 逻辑上相等的(即位于同一个 RelSet 中)任意一个 RelSubset 的真实 importance 除以 2
真实importance的计算规则如下:
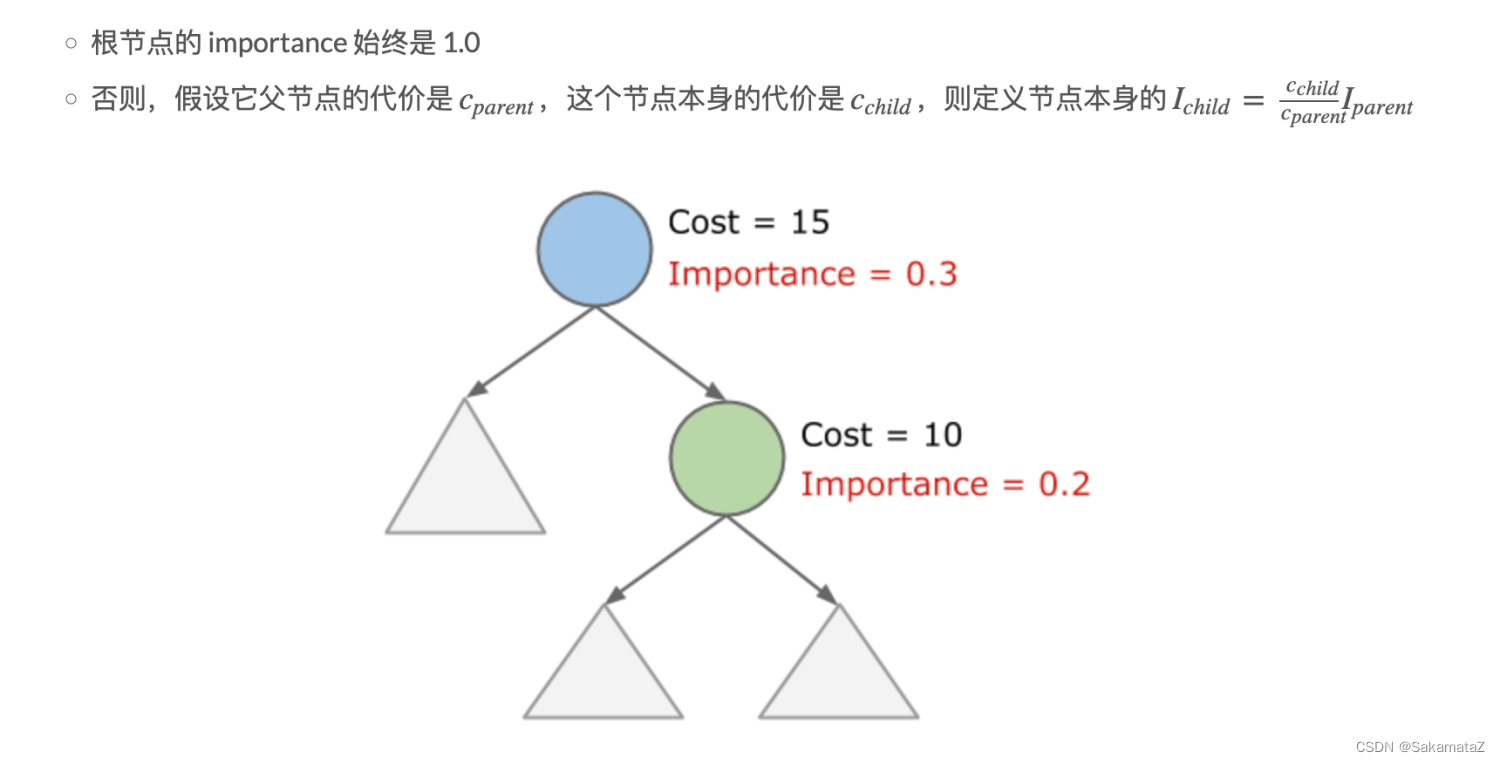

Join reorder
大部分的算法基于connectivity-heuristic,也就是说,只考虑equl-join
基于连接次序优化的动态规划算法
对于假设所有的连接都是自然连接的n个关系的集合,动态规划算法的复杂度为3^n
归并连接可以产生有序的结果,对于后面的排序可能有用(interesting sort order)。
目前我们用spark的连接算法,这条暂时没用。
IKKBZ算法
left-deep tree和bushy tree
left-deep tree 左深树
连接运算符的右侧输入都是具体关系,右子树必和左子树的节点之一有共享谓词。
左深树适合一般场景的优化。System R优化器只考虑左深树的优化,时间代价是n!,加入动态规划后,可以在n*2^n时间内找到最佳连接次序。
bushy-tree
适合多路连接和并行优化,但是很复杂。
不引入交叉乘的充要条件在于给定关系的父级必须已经得到。
ASI
简单来说就是等价谓词替换原则
定义rank函数:
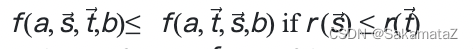
成本函数
谓词的选择性指的是谓词对查询结果的过滤能力
对于join来说可以有如下定义:
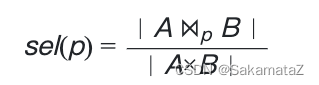
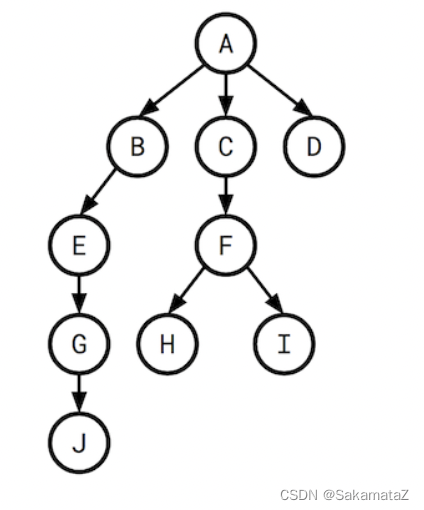
我们将查询图视为一个有根树,我们说H的选择性指的是F和H之间的选择性。
行数和选择性之间则有如下关系(行数*选择性):
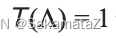
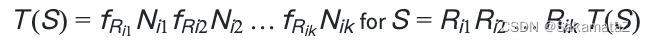
成本函数定义如下:

我们可以根据成本函数定义rank函数:
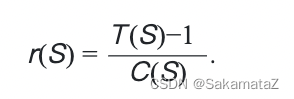
下面是对于ASI的证明:
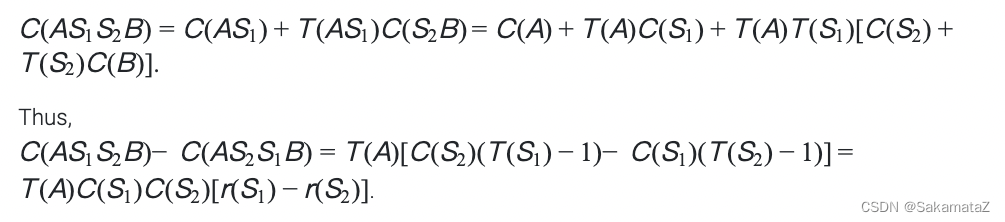
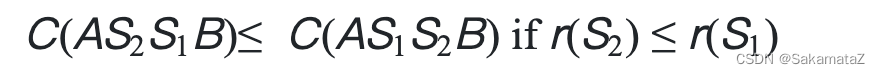
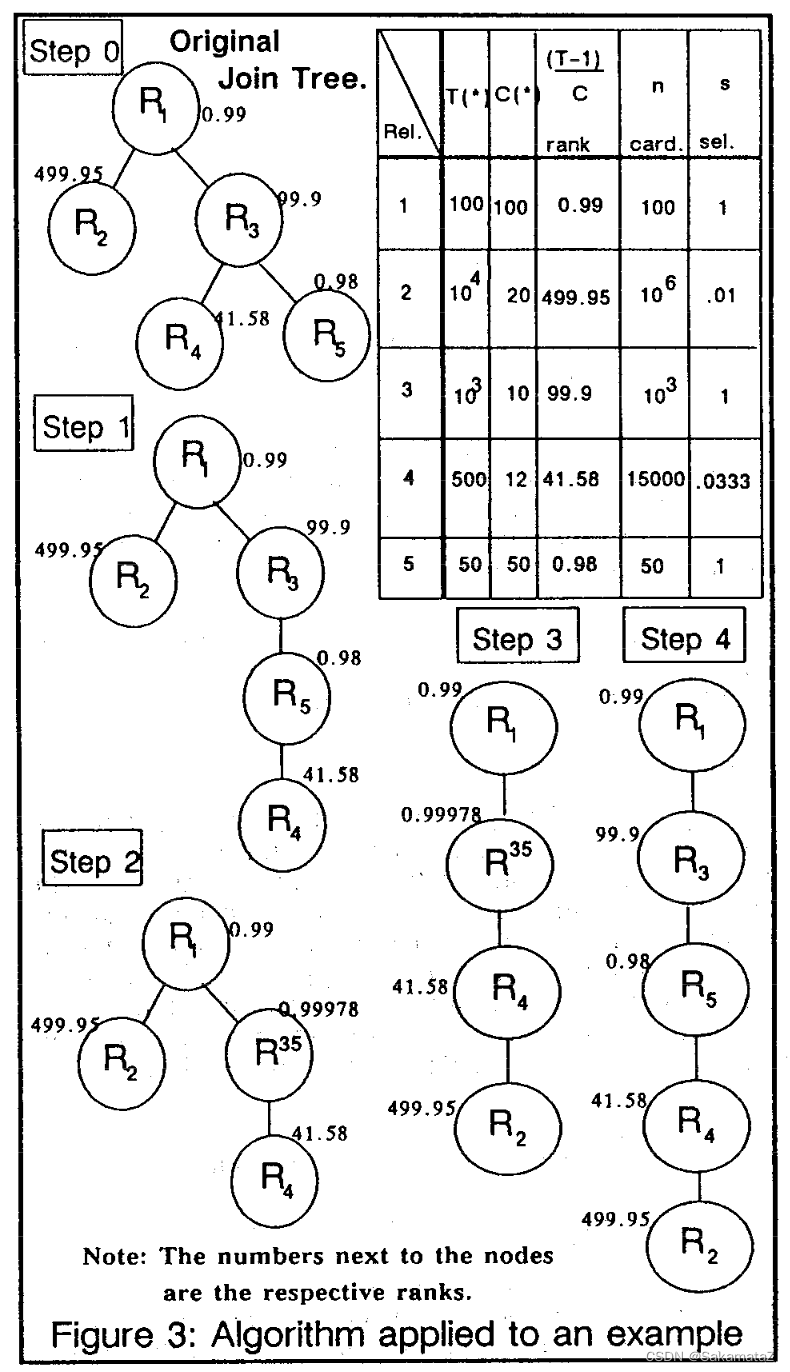
归一化
Calcite实践
MultiJoinOptimizeBushyRule
第一部分进行初始化,unusedEdges存放join过滤条件(两个relnode之间)
final MultiJoin multiJoinRel = call.rel(0);final RexBuilder rexBuilder = multiJoinRel.getCluster().getRexBuilder();final RelBuilder relBuilder = call.builder();final RelMetadataQuery mq = call.getMetadataQuery();final LoptMultiJoin multiJoin = new LoptMultiJoin(multiJoinRel);final List<Vertex> vertexes = new ArrayList<>();int x = 0;for (int i = 0; i < multiJoin.getNumJoinFactors(); i++) {final RelNode rel = multiJoin.getJoinFactor(i);double cost = mq.getRowCount(rel);vertexes.add(new LeafVertex(i, rel, cost, x));x += rel.getRowType().getFieldCount();}assert x == multiJoin.getNumTotalFields();final List<Edge> unusedEdges = new ArrayList<>();for (RexNode node : multiJoin.getJoinFilters()) {unusedEdges.add(multiJoin.createEdge(node));}
第二步选出成本(此处就是行数)差异最大的过滤条件
选一个行数较小的vertex作为majorFactor,另一个作为minorFactor
// Comparator that chooses the best edge. A "good edge" is one that has// a large difference in the number of rows on LHS and RHS.final Comparator<LoptMultiJoin.Edge> edgeComparator =new Comparator<LoptMultiJoin.Edge>() {@Override public int compare(LoptMultiJoin.Edge e0, LoptMultiJoin.Edge e1) {return Double.compare(rowCountDiff(e0), rowCountDiff(e1));}private double rowCountDiff(LoptMultiJoin.Edge edge) {assert edge.factors.cardinality() == 2 : edge.factors;final int factor0 = edge.factors.nextSetBit(0);final int factor1 = edge.factors.nextSetBit(factor0 + 1);return Math.abs(vertexes.get(factor0).cost- vertexes.get(factor1).cost);}};final List<Edge> usedEdges = new ArrayList<>();for (;;) {final int edgeOrdinal = chooseBestEdge(unusedEdges, edgeComparator);if (pw != null) {trace(vertexes, unusedEdges, usedEdges, edgeOrdinal, pw);}final int[] factors;if (edgeOrdinal == -1) {// No more edges. Are there any un-joined vertexes?final Vertex lastVertex = Util.last(vertexes);final int z = lastVertex.factors.previousClearBit(lastVertex.id - 1);if (z < 0) {break;}factors = new int[] {z, lastVertex.id};} else {final LoptMultiJoin.Edge bestEdge = unusedEdges.get(edgeOrdinal);// For now, assume that the edge is between precisely two factors.// 1-factor conditions have probably been pushed down,// and 3-or-more-factor conditions are advanced. (TODO:)// Therefore, for now, the factors that are merged are exactly the// factors on this edge.assert bestEdge.factors.cardinality() == 2;factors = bestEdge.factors.toArray();}// Determine which factor is to be on the LHS of the join.final int majorFactor;final int minorFactor;if (vertexes.get(factors[0]).cost <= vertexes.get(factors[1]).cost) {majorFactor = factors[0];minorFactor = factors[1];} else {majorFactor = factors[1];minorFactor = factors[0];}final Vertex majorVertex = vertexes.get(majorFactor);final Vertex minorVertex = vertexes.get(minorFactor);
遍历unusedEdges,加入newFactors,对之前选出的majorVertex和minorVertex进行归一化并且加入vertexes
// Find the join conditions. All conditions whose factors are now all in// the join can now be used.final int v = vertexes.size();final ImmutableBitSet newFactors =majorVertex.factors.rebuild().addAll(minorVertex.factors).set(v).build();final List<RexNode> conditions = new ArrayList<>();final Iterator<LoptMultiJoin.Edge> edgeIterator = unusedEdges.iterator();while (edgeIterator.hasNext()) {LoptMultiJoin.Edge edge = edgeIterator.next();if (newFactors.contains(edge.factors)) {conditions.add(edge.condition);edgeIterator.remove();usedEdges.add(edge);}}double cost =majorVertex.cost* minorVertex.cost* RelMdUtil.guessSelectivity(RexUtil.composeConjunction(rexBuilder, conditions));final Vertex newVertex =new JoinVertex(v, majorFactor, minorFactor, newFactors,cost, ImmutableList.copyOf(conditions));vertexes.add(newVertex);
归一化之后进行选择性的重新计算,之后进入下一轮
// Re-compute selectivity of edges above the one just chosen.// Suppose that we just chose the edge between "product" (10k rows) and// "product_class" (10 rows).// Both of those vertices are now replaced by a new vertex "P-PC".// This vertex has fewer rows (1k rows) -- a fact that is critical to// decisions made later. (Hence "greedy" algorithm not "simple".)// The adjacent edges are modified.final ImmutableBitSet merged =ImmutableBitSet.of(minorFactor, majorFactor);for (int i = 0; i < unusedEdges.size(); i++) {final LoptMultiJoin.Edge edge = unusedEdges.get(i);if (edge.factors.intersects(merged)) {ImmutableBitSet newEdgeFactors =edge.factors.rebuild().removeAll(newFactors).set(v).build();assert newEdgeFactors.cardinality() == 2;final LoptMultiJoin.Edge newEdge =new LoptMultiJoin.Edge(edge.condition, newEdgeFactors,edge.columns);unusedEdges.set(i, newEdge);}}
最后一段,根据新的vertexes次序建立relnode节点
// We have a winner!
List<Pair<RelNode, TargetMapping>> relNodes = new ArrayList<>();
for (Vertex vertex : vertexes) {if (vertex instanceof LeafVertex) {LeafVertex leafVertex = (LeafVertex) vertex;final Mappings.TargetMapping mapping =Mappings.offsetSource(Mappings.createIdentity(leafVertex.rel.getRowType().getFieldCount()),leafVertex.fieldOffset,multiJoin.getNumTotalFields());relNodes.add(Pair.of(leafVertex.rel, mapping));} else {JoinVertex joinVertex = (JoinVertex) vertex;final Pair<RelNode, Mappings.TargetMapping> leftPair =relNodes.get(joinVertex.leftFactor);RelNode left = leftPair.left;final Mappings.TargetMapping leftMapping = leftPair.right;final Pair<RelNode, Mappings.TargetMapping> rightPair =relNodes.get(joinVertex.rightFactor);RelNode right = rightPair.left;final Mappings.TargetMapping rightMapping = rightPair.right;final Mappings.TargetMapping mapping =Mappings.merge(leftMapping,Mappings.offsetTarget(rightMapping,left.getRowType().getFieldCount()));if (pw != null) {pw.println("left: " + leftMapping);pw.println("right: " + rightMapping);pw.println("combined: " + mapping);pw.println();}final RexVisitor<RexNode> shuttle =new RexPermuteInputsShuttle(mapping, left, right);final RexNode condition =RexUtil.composeConjunction(rexBuilder, joinVertex.conditions);final RelNode join = relBuilder.push(left).push(right).join(JoinRelType.INNER, condition.accept(shuttle)).build();relNodes.add(Pair.of(join, mapping));}if (pw != null) {pw.println(Util.last(relNodes));}
Join 算法选择
关联子查询优化
我们将连接外部查询和子查询的算子叫做CorrelatedJoin(也被称之为lateral join, dependent join、apply算子等等。它的左子树我们称之为外部查询(input),右子树称之为子查询(subquery)。


注:bag语义,允许元素重复出现,和set语义正交
为什么要消除关联子查询?
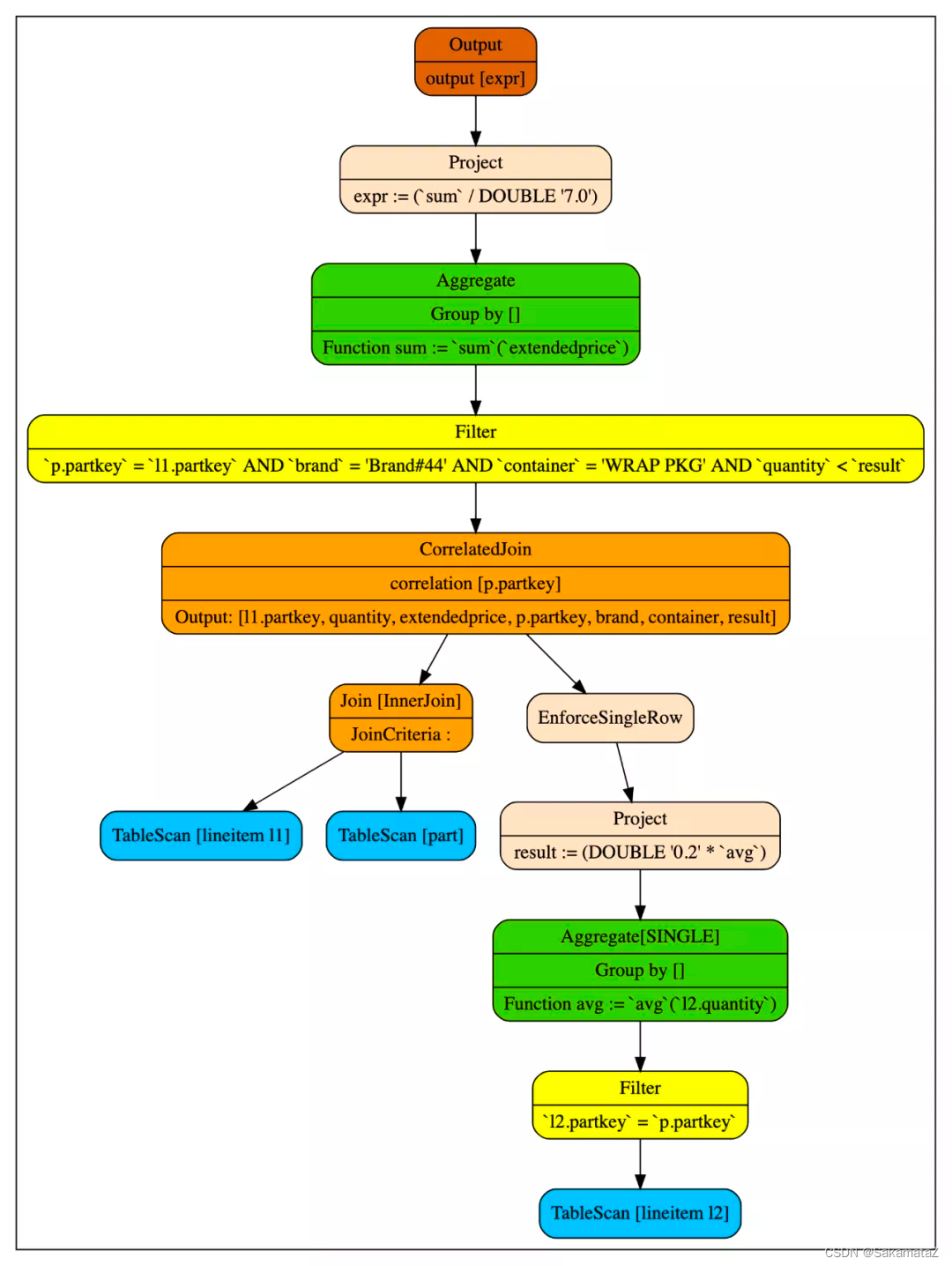
CorrelatedJoin这个算子打破了以往对逻辑树自上而下的执行模式。普通的逻辑树都是从叶子节点往根结点执行的,但是CorreltedJoin的右子树会被带入左子树的行的值反复的执行。
基本消除规则
如果 Apply 的右边不包含来自左边的参数(或者只包含filter参数),那它就和直接 Join 是等价的
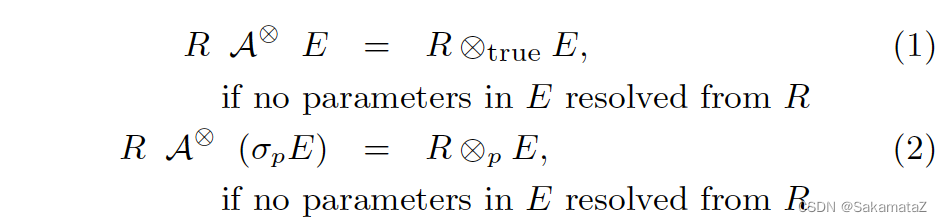
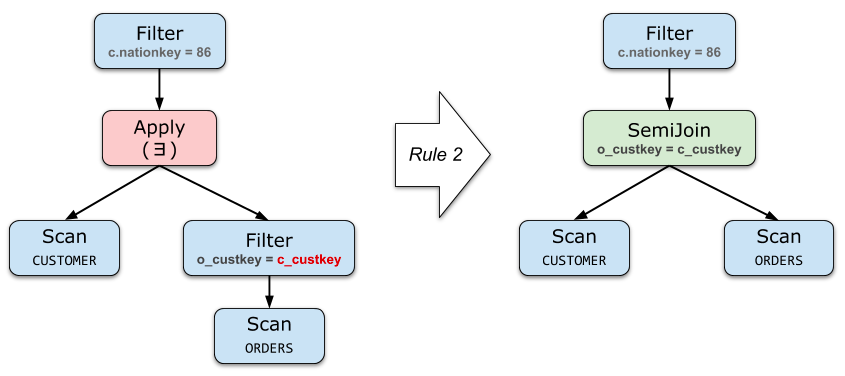
project和filter去关联化
尽可能把 Apply 往下推、把 Apply 下面的算子向上提。
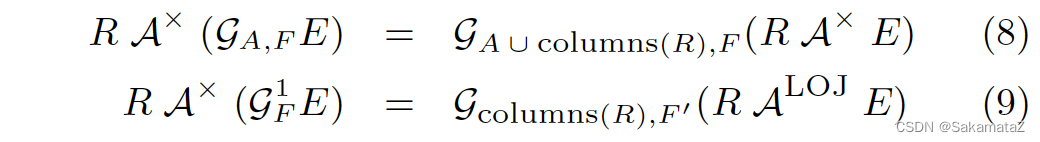
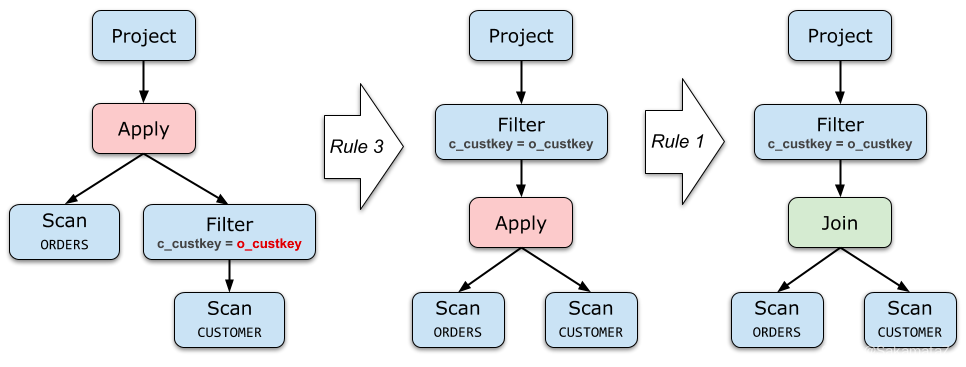
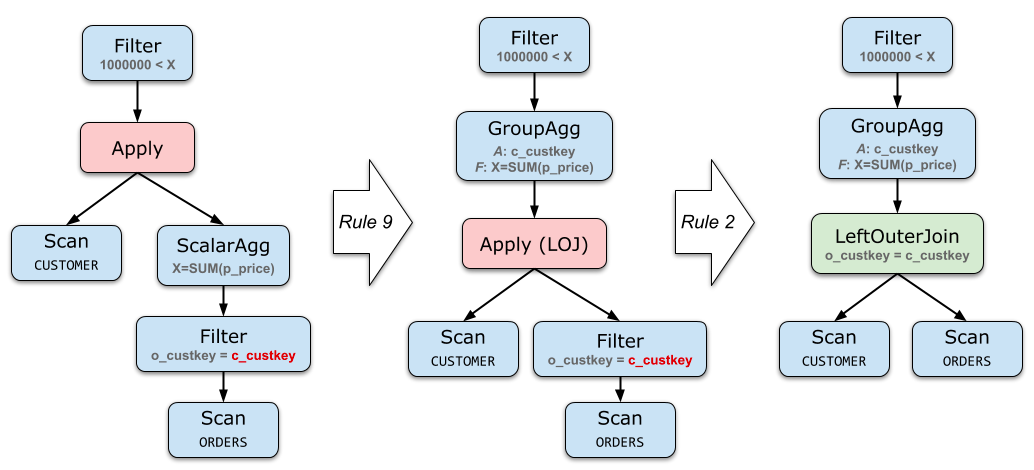
Aggregate的去关联化
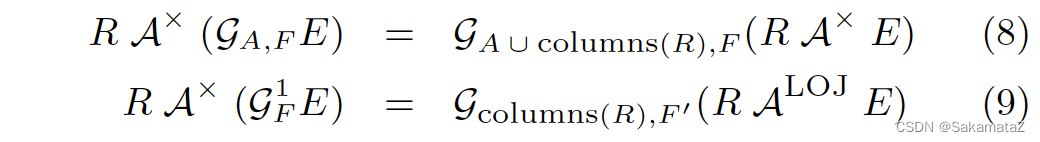
SELECT c_custkey
FROM CUSTOMER
WHERE 1000000 < (SELECT SUM(o_totalprice)FROM ORDERSWHERE o_custkey = c_custkey
)
// 等价于
select sum(p_price) > 1000000 from CUSTOMER.o_custkey left join ORDERS.c_custkey
on CUSTOMER.o_custkey = ORDERS.c_custkey group by ORDERS.c_custkey
集合运算的去关联化
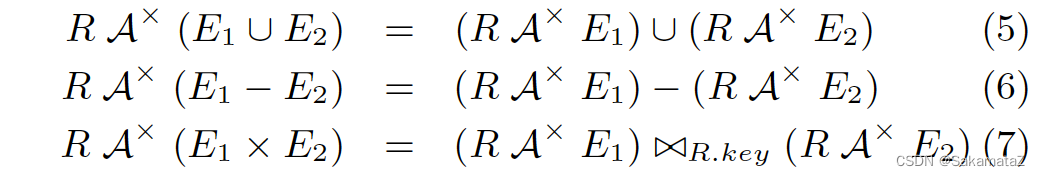
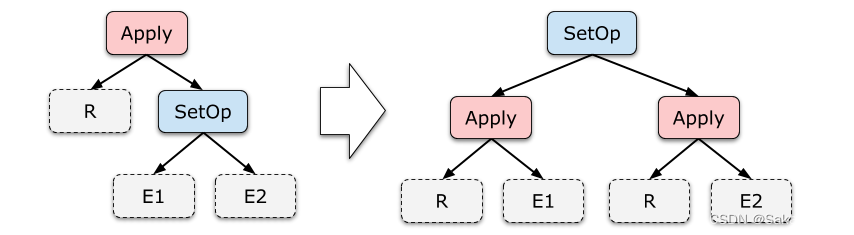
这一组规则很少能派上用场。在 TPC-H 的 Schema 下甚至很难写出一个带有 Union All 的、有意义的子查询。
相关文章:

SQL编译优化原理
最近在团队的OLAP引擎上做了一些SQL编译优化的工作,整理到了语雀上,也顺便发在博客上了。SQL编译优化理论并不复杂,只需要掌握一些关系代数的基础就比较好理解;比较困难的在于reorder算法部分。 文章目录 基础概念关系代数等价 j…...

qt signal slots lambda
这里用到了qt的版本检测 连接 Combox的currentIndexChanged事件 emit来触发处理的事件 ,进行业务或逻辑处理 这样的写法是lambda表达式的写法,和c#中的 (obj)>{ //todo } 类同 [](int indx){ //todo } #if QT_VERSION > QT_VERSION_CHECK(5,7,0)c…...

Spring【声明式事务】
事务简介 把一组业务当成一个业务来做;要么都成功,要么都失败!事务在项目开发中,十分重要,涉及到数据一致性的问题,需要十分注意!确保完整性和一致性! 事务的ACID原则:…...

【雕爷学编程】MicroPython动手做(17)——掌控板之触摸引脚2
知识点:什么是掌控板? 掌控板是一块普及STEAM创客教育、人工智能教育、机器人编程教育的开源智能硬件。它集成ESP-32高性能双核芯片,支持WiFi和蓝牙双模通信,可作为物联网节点,实现物联网应用。同时掌控板上集成了OLED…...

pytorch 中 view 和reshape的区别
在 PyTorch(一个流行的深度学习框架)中, reshape 和 view 都是用于改变张量(tensor)形状的方法,但它们在实现方式和使用上有一些区别。下面是它们之间的主要区别: 实现方式: reshap…...
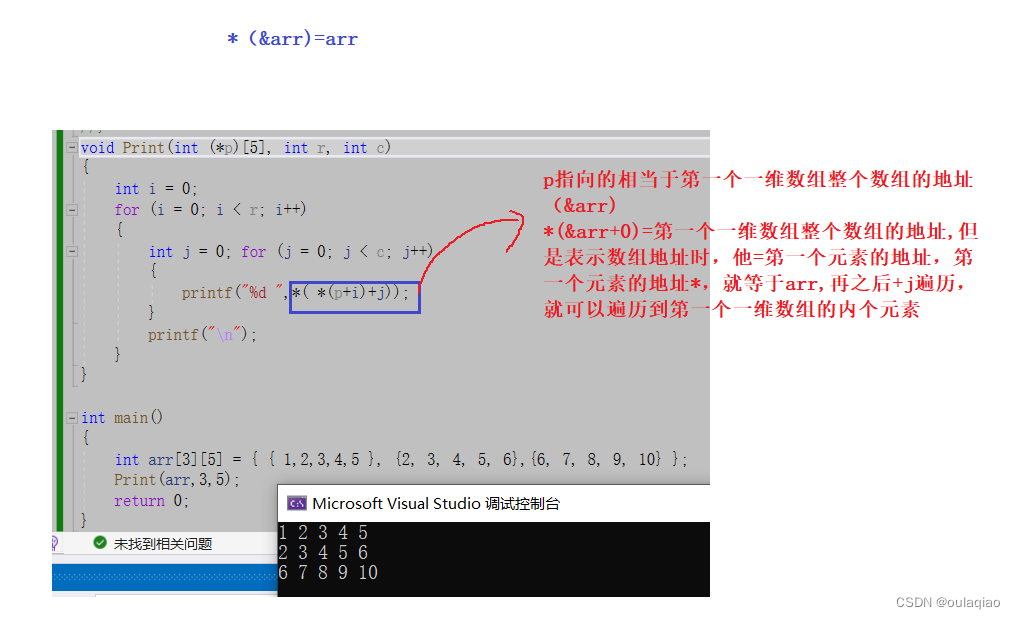
认识数组指针
文章目录 数组指针的定义数组指针的应用 数组指针的定义 类比 整形数组——存放整形的数组 指针数组——存放指针的数组 整形指针——存放整形地址的指针 数组指针——存放数组地址的指针 深度理解 在之前我们知道:数组名表示首元素地址,但是有…...
SSM面试题-Spring容器的启动流程
解答: 1. BeanDefinitionReader读取配置文件(xml yml properties),创建BeanDefinition(存储bean的定义信息) 2. 配置文件读取成功后,将相应的配置转换成 BeanDefinition 的对象实例保存在DefaultListableBeanFactory#beanDefinitionMap 中 3. 根据配置的 BeanFacto…...
)
Vue 3:玩一下web前端技术(八)
前言 本章内容为VUE基础与相关技术讨论。 上一篇文章地址: Vue 3:玩一下web前端技术(七)_Lion King的博客-CSDN博客 下一篇文章地址: (暂无) 一、基础 官方文档:创建一个 Vue…...

AI绘画Stable Diffusion原理之Autoencoder-Latent
前言 传送门: stable diffusion:Git|论文 stable-diffusion-webui:Git Google Colab Notebook:Git kaggle Notebook:Git 今年AIGC实在是太火了,让人大呼许多职业即将消失,比如既能帮…...

C++核心知识点总结
学习一门新的程序设计语言得到最好方法就是练习编写程序! C基础 变量和基本类型 基本内置类型 定义解释 算术类型 整型:包括字符和布尔类型,bool、char、wchar_t、char16_t、char32_t、short、int、long、long long、 浮点型:…...
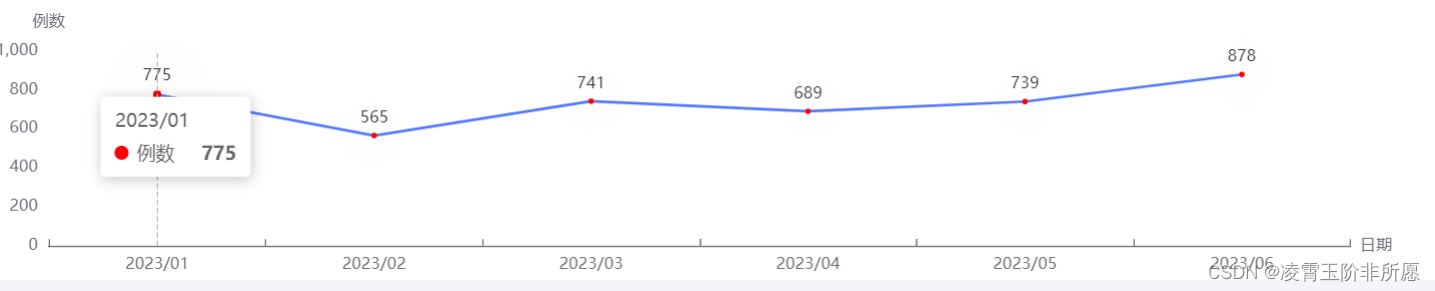
echart折线图,调节折线点和y轴的间距(亲测可用)
options代码: options {tooltip: {trigger: axis, //坐标轴触发,主要在柱状图,折线图等会使用类目轴的图表中使用。},xAxis: {type: category,//类目轴,适用于离散的类目数据,为该类型时必须通过 data 设置类目数据。…...

Power BI-云端报表定时刷新--ODBC、MySQL、Oracle等其他本地数据源的刷新(二)
ODBC数据源 一些小众的数据源无法直接连接,需要通过微软系统自带的应用“ODBC数据源”连接。 1.首次使用应安装对应数据库的ODBC驱动程序,Mysql的ODBC驱动需要手动安装 2.在web服务中进行数据源的配置 Mysql数据源 1.Powerbi与Gateway第一次连SQL…...

redis 淘汰策略和持久化
文章目录 一、淘汰策略1.1 背景1.2 淘汰策略 二、持久化2.1 AOF日志2.1.1 AOF配置2.1.2 AOF策略2.1.3 AOF缺点2.1.4 AOF Rewrite2.1.5 AOF Rewrite配置2.1.6 AOF Rewrite缺点2.1.7 fork进程时的写时复制2.1.8 大key对持久化的影响 2.2 RDB快照2.2.1 RDB配置2.2.2 RDB缺点 2.3 混…...
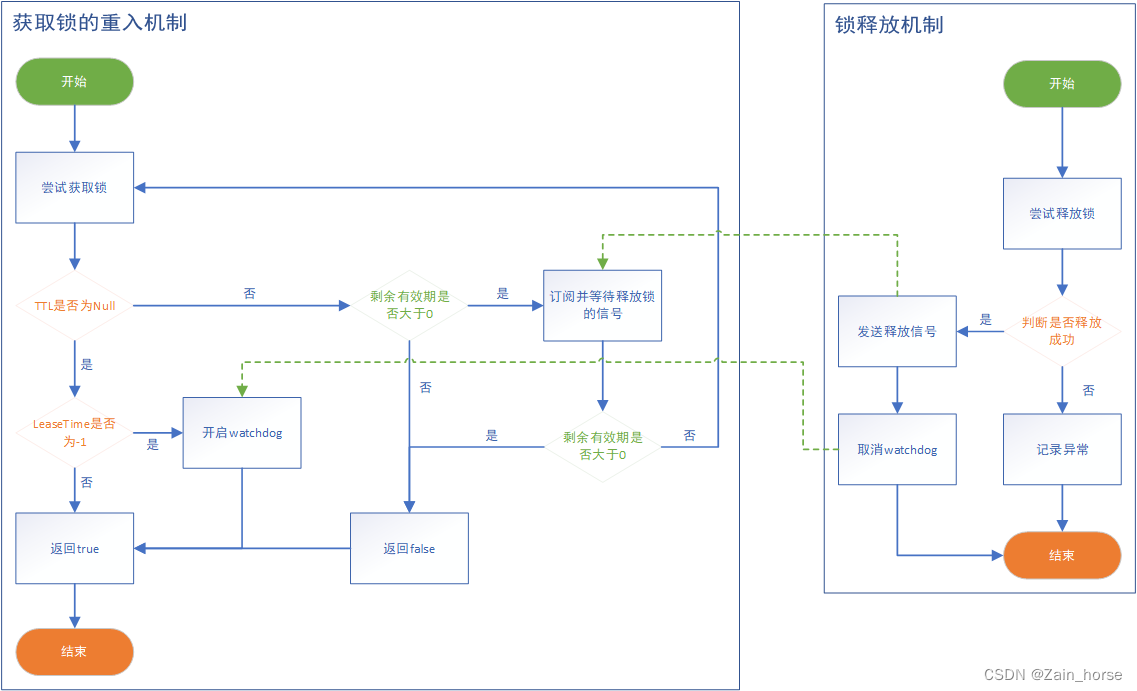
Redis学习路线(6)—— Redis的分布式锁
一、分布式锁的模型 (一)悲观锁: 认为线程安全问题一定会发生,因此在操作数据之前先获取锁,确保线程串行执行。例如Synchronized、Lock都属于悲观锁。 优点: 简单粗暴缺点: 性能略低 &#x…...
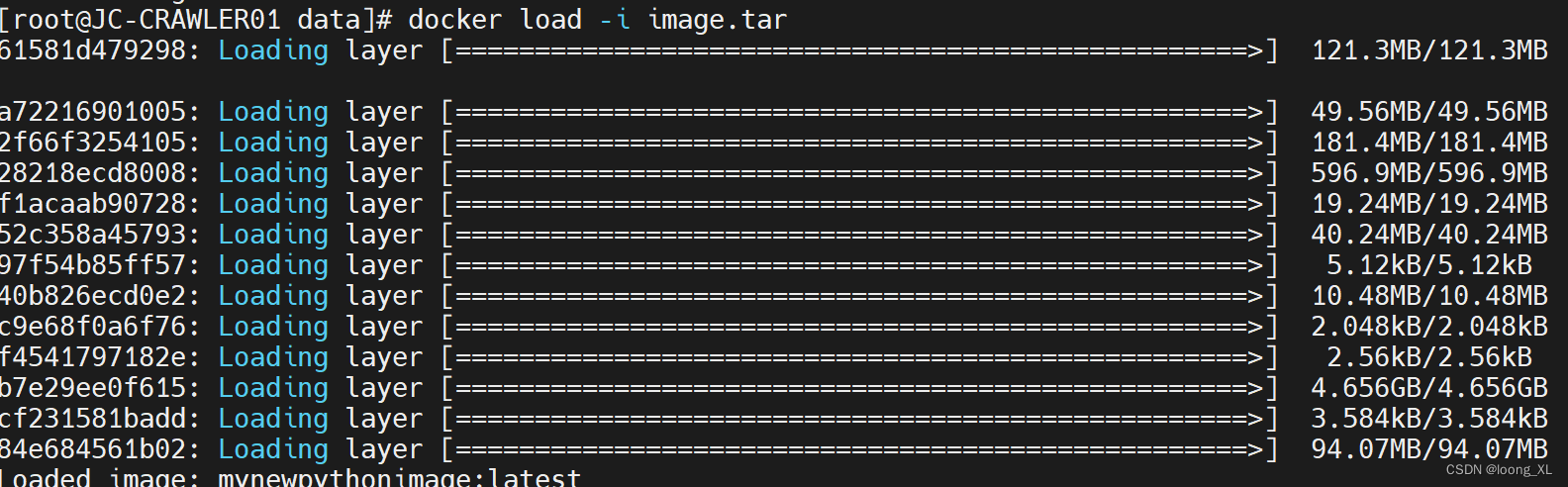
一、创建自己的docker python容器环境;支持新增python包并更新容器;离线打包、加载image
1、创建自己的docker python容器环境 参考:https://blog.csdn.net/weixin_42357472/article/details/118991485 首先写Dockfile,注意不要有txt等后缀 Dockfile # 使用 Python 3.9 镜像作为基础 FROM python:3.9# 设置工作目录 WORKDIR /app# 复制当前…...
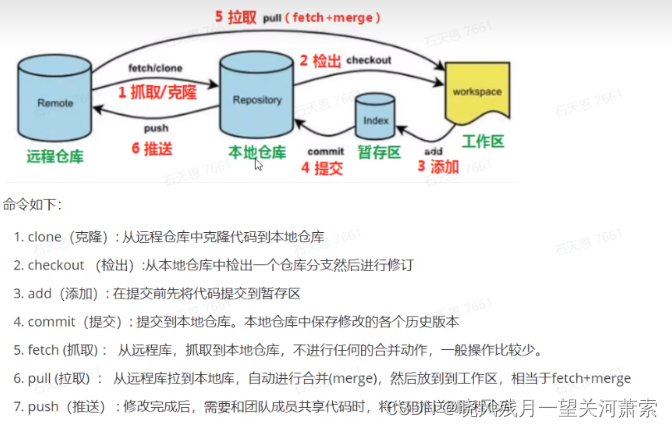
【Git】git企业开发命令整理,以及注意点
1.git企业开发过程 业务的分支大概有以下几个: master:代码随时可能上线 develop:代码最新 feature/xxx:实际业务开发分支 release/xxx:预发布分支 fix:修复bug分支 过程大概是这样的: 首…...

使用Django自带的后台管理系统进行数据库管理的实例
Django自带的后台管理系统主要用来对数据库进行操作和管理。它是Django框架的一个强大功能,可以让你快速创建一个管理界面,用于管理你的应用程序的数据模型。 使用Django后台管理系统,你可以轻松地进行以下操作: 数据库管理&…...
1254 - 1266 题)
leetcode解题思路分析(一百四十五)1254 - 1266 题
统计封闭岛屿的数目 二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。请返回 封闭岛屿 的数目。 BFS或者DFS…...

使用 GORM 连接数据库并实现增删改查操作
步骤 1:安装 GORM 首先,我们需要安装 GORM 包。在终端中运行以下命令: shell go get -u gorm.io/gorm 步骤 2:导入所需的包 在 Go 代码的开头导入以下包: import ("gorm.io/driver/mysql" // 如果你使用…...

kafka集群搭建(Linux环境)
zookeeper搭建,可以搭建集群,也可以单机(本地学习,没必要搭建zookeeper集群,单机完全够用了,主要学习的是kafka) 1. 首先官网下载zookeeper:Apache ZooKeeper 2. 下载好之后上传到…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
