基于解析法和遗传算法相结合的配电网多台分布式电源降损配置(Matlab实现)
目录
1 概述
2 数学模型
2.1 问题表述
2.2 DG的最佳位置和容量(解析法)
2.3 使用 GA 进行最佳功率因数确定和 DG 分配
3 仿真结果与讨论
3.1 33 节点测试配电系统的仿真
3.2 69 节点测试配电系统仿真
4 结论
1 概述
为了使系统网损达到最低值,人们提出了多种方法来确定分布式发电机组的最优位置和容量。
本文将解析法和遗传算法相结合,用于配电网中多个分布式电源的优化配置,使系统网损最小。
这种组合保证了多个分布式发电机组配置的收敛精度和速度。在本文中,在配电网网损最小化时,同时考虑分布式电源的有功功率、功率因数和位置。如果DG是由DG所有者安装的,则该实用程序将仅规定DG的最大发电量。但是,如果DG是由它安装的,则DG的大小和位置都将由该实用程序确定。将该方法应用于33节点和69节点试验配电网。仿真结果表明,与其他方法相比,该方法具有更低的损耗。
本文提出了一种新的方法,这是一种混合方法,它使用遗传算法搜索大范围的位置组合和分布式电源的功率因数,并采用解析方法计算每个分布式电源的位置和容量。虽然这是以要求预先指定DG单位的数量为代价来实现的,但这为检验不同数量 DG 战略布局的好处开辟了潜力。
将该方法应用于33节点和69节点试验配电网,结果表明了该方法在配电网分布式发电机组优化配置中的准确性和有效性。本文创新点如下:
分析和启发式搜索方法相结合,同时实现高速和准确的收敛。考虑将松弛节点的有功潮流对分布式电源产生的有功功率的依赖性作为最小化配电网网损的新约束。
利用分布式电源最优输出有功功率的确定性方程,根据网损系数和网络需求,对配电网网损最小化问题进行了解析解。在最小化配电网损耗的过程中,同时考虑分布式电源的有功功率、功率因数和位置。
本论文的结构如下:第二节数学模型
第三节对多个DG单元放置的仿真和结果进行了研究和讨论。最后,第四节对本文进行了总结。
2 数学模型
2.1 问题表述
网络中的有功网损可以表示为不同机组发电量的函数,根据下面的关系,称为Kron方程:

等式(1)可以表示为以下矩阵形式:
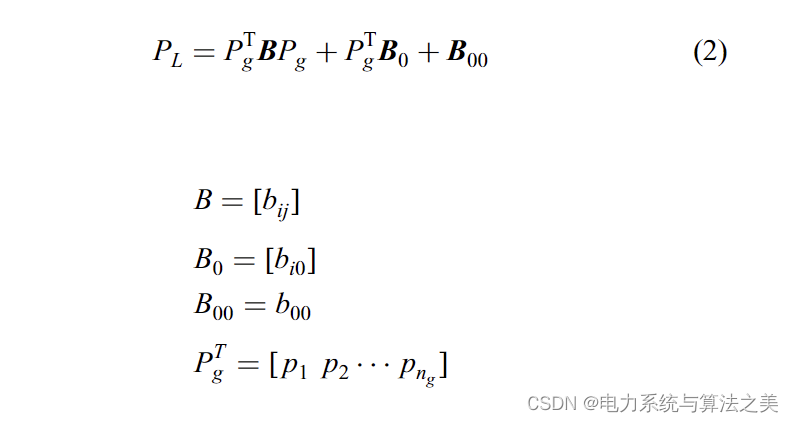
在(2)中,矩阵B、B0和B00是损耗系数矩阵。一般来说,这些系数不是恒定的,并且依赖于负荷值和发电量。但是,它们可以在系统运行的基本情况下计算。
本文考虑了如下假设:配电网是一个在松弛节点馈电的放射状系统,用数字1标识并连接到子配电电网络或输电网络,分布式电源具有恒定的功率因数。
2.2 DG的最佳位置和容量(解析法)
假设在使用恒定功率因数,
,.....
的母线Kn1、Kn2、...中安装了Ng个DG单元。假设松弛母线为发电单元,则该网络中有
个发电单元。网损可按(1)计算。
假设DG安装在母线2、3、…、+1上。如果(1)相对于
的导数为零,则网络损耗将是最小的。
应当注意,...
在(1)中指示由不同DG产生的功率是独立的,并且由松弛母线
产生的功率如下所示依赖于这些变量:
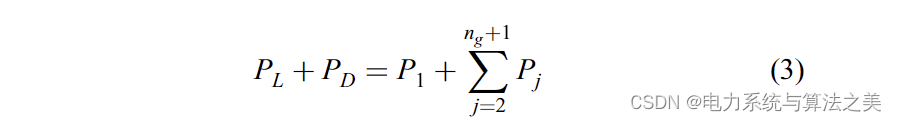
应当注意,假设PD在网络的特定状态下是恒定的。
对(3)进行微分,可以得到 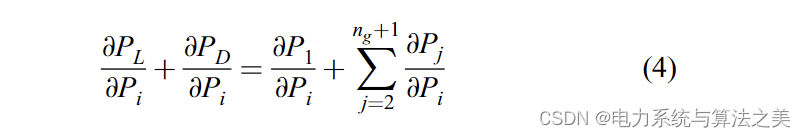
由于 ∂PL/∂Pi 和 ∂PD/∂Pi 等于 0,所以 (4) 可以写成如下:
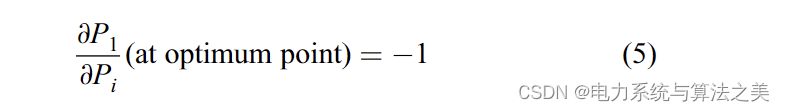
如(5)所示,P1取决于不同DG的发电量。另一方面,在系统损耗最小的情况下,松弛母线产生的有功功率变化与DG机组产生的有功功率变化的比值等于-1。为了使(1)在(3)的约束下达到最小,采用了拉格朗日松弛法,具体如下:
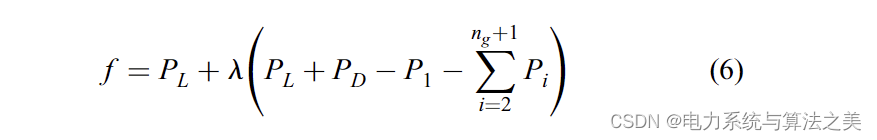
偏微分函数应该等于零,也就是:
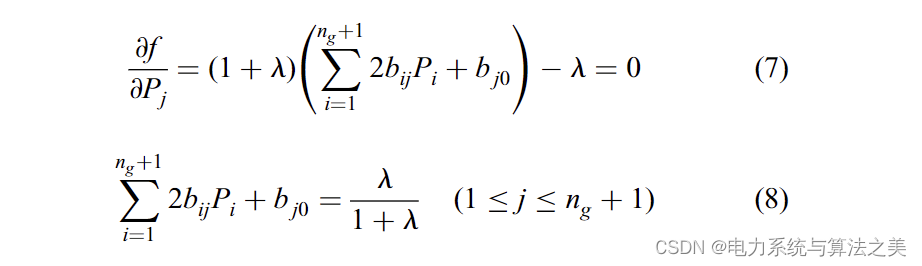
方程(8)可以写成矩阵形式,如下:
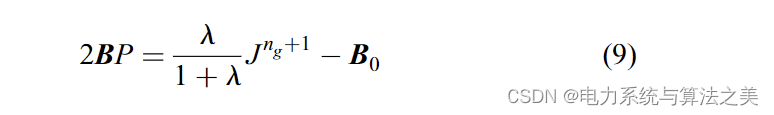
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
可以使用以下等式从 (9) 计算 P:

其中 x、E 和 F 可以分别根据以下等式计算:
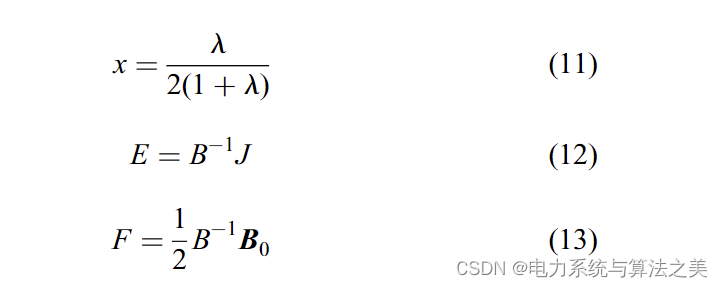
P的每个元素确定如下:
![]()
对于已知的x值,可以根据(10)计算出最佳的,将(10)-(14)代入(3),可以写出以下公式:
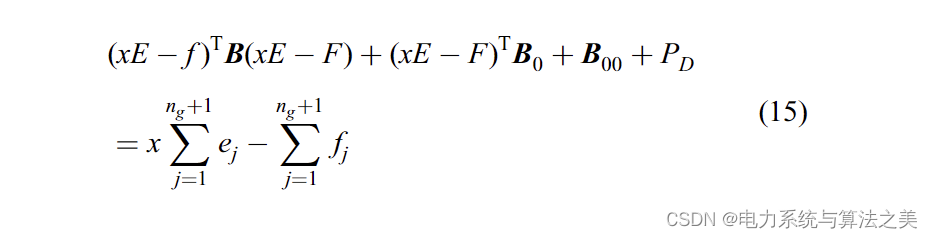
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
展开 (15) 得出以下等式:
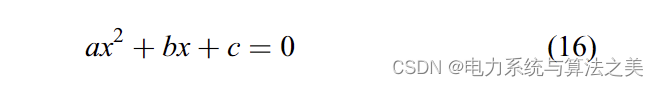
其中参数 a、b 和 c 基于以下等式计算:
a通过下式进行计算:

通过将 E 从 (12) 中代入, (17) 可以写为:
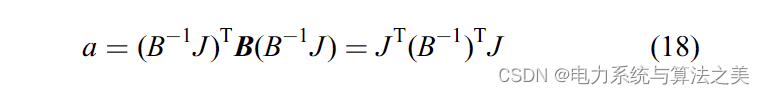
由于 B = BT, (18) 可简化如下:
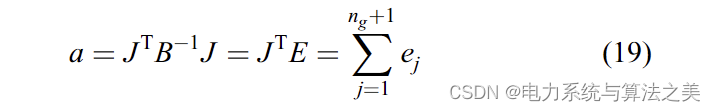
b 根据以下等式计算:
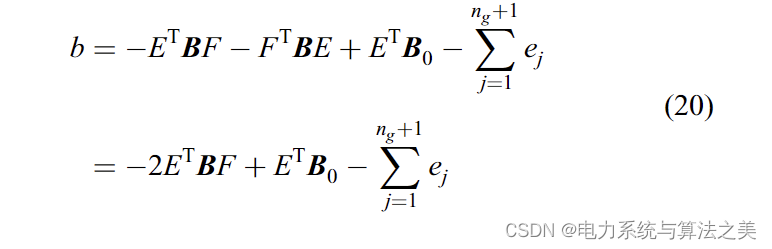
考虑 (13),b 可以根据以下等式计算:
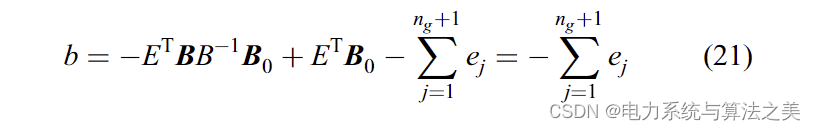
最后,c可以按下式进行计算:
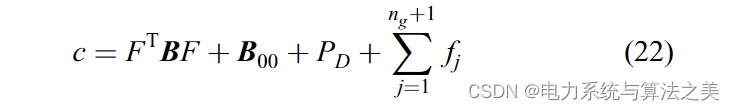
等式 (16) 有如下两个根:
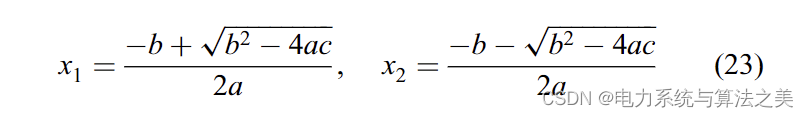
由于 b 是负数 [考虑 (21)],x1 是一个很大的数,对应的 Pi 也有很大的值 [根据 (14)]。这个答案是不可接受的,因为单位中的 Pi 太大了。因此,以下答案是唯一可以接受的答案:
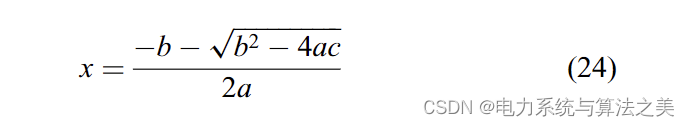
使用 (10)–(24),确定 的最佳值。
2.3 使用 GA 进行最佳功率因数确定和 DG 分配
在本节中,DG功率因数及其位置被确定为具有系统损耗的最小值。遗传算法是一种通用的优化方法,已被用于不同领域的优化问题。遗传算法分几个步骤进行,如:
在本文中,每个DG单元的优化问题都考虑了三个变量。这些变量是DG的有功功率、DG的功率因素和DG的位置。DG的有功功率是通过解析方案和数学方法得到的(24)。功率因数和DG的位置分别通过使用连续和离散的GA来确定。在GA中,染色体是问题变量,也就是功率因数和DG的位置。因此,假设有ng个DG单元,GA中染色体的长度将等于2ng,包括ng个功率因数的基因(PF1, PF2, ..., PFn)和ng个DG连接位置的基因(D1, D2, ..., Dn)。

图1 本文所考虑的染色体形态。
换句话说,在GA过程的第一步,一组可能的答案被随机产生,这些答案被称为方案或染色体。本文认为一个染色体的形式如图1所示。在下一步中,将根据每个染色体的适合度为其分配一个数字,作为可能的答案。上述数字由适应度函数决定,适应度函数将由GA进行优化。最后,GA通过选择操作符并根据染色体的适配度选择一些染色体进行交叉、变异和替换操作。这些运算符产生一个新的群体,该过程将被重复,直到达到停止条件。为了计算与染色体相对应的适配函数,根据(2)计算网络损失,并利用(24)确定DG的最佳功率世代。在功率流运行后,根据(1)确定电力系统损失,并将其分配给一个染色体作为其适配值。
![]()
GA 应该通过改变功率因数和不同 DG 的位置来寻找适应度函数的最小值。本文采用分析方法和启发式搜索方法相结合的方法解决了分布式电源优化分配问题,如图 2 所示。使用该方法的主要好处如下:
由于分布式电源的功率余量代数太广,GA收敛速度慢,可能无法得出准确的解。本文采用遗传算法确定分布式发电机组的安装位置及其功率因数,并采用解析法确定分布式发电机组产生的最佳功率。
仅使用解析方法会导致复杂且非线性的方程,因为应计算损耗系数相对于 DGs 功率因数的微分,并且损耗系数是 DGs 功率因数的非线性和复杂函数。此外,DGs 位置是一个离散参数,它对 DG 位置的导数是没有意义的。因此,启发式搜索算法应该被用于优化DG分配。考虑到这两个问题,本文提出了分析和启发式搜索相结合的方法。
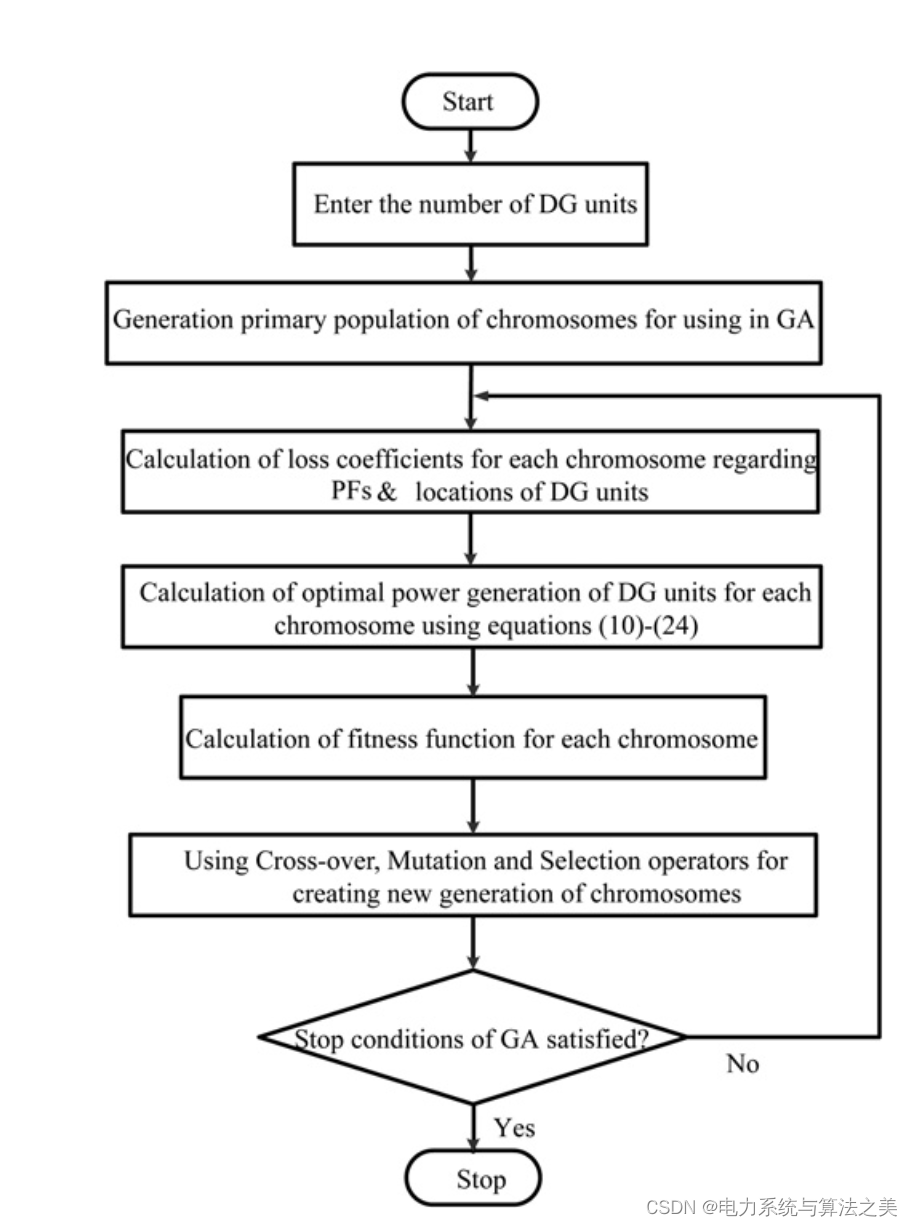
图2 所提出方法的流程图
3 仿真结果与讨论
将该方法应用于图3和图4所示的两个试验配电网(33节点和69节点系统)。该算法在Matlab环境下实现,并使用MATPOWER软件进行潮流计算。
在本研究中,分布式发电有两种不同的运行模式:分布式发电只产生有功功率(单位功率因数模式)和分布式发电可以产生有功和无功(非单位功率因数模式)。
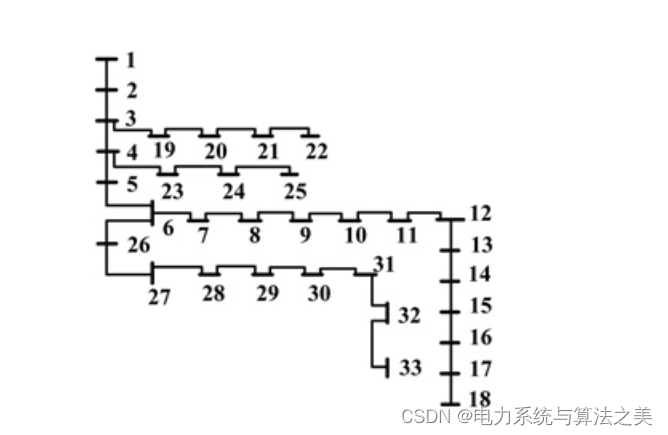
图3 33节点测试配电系统
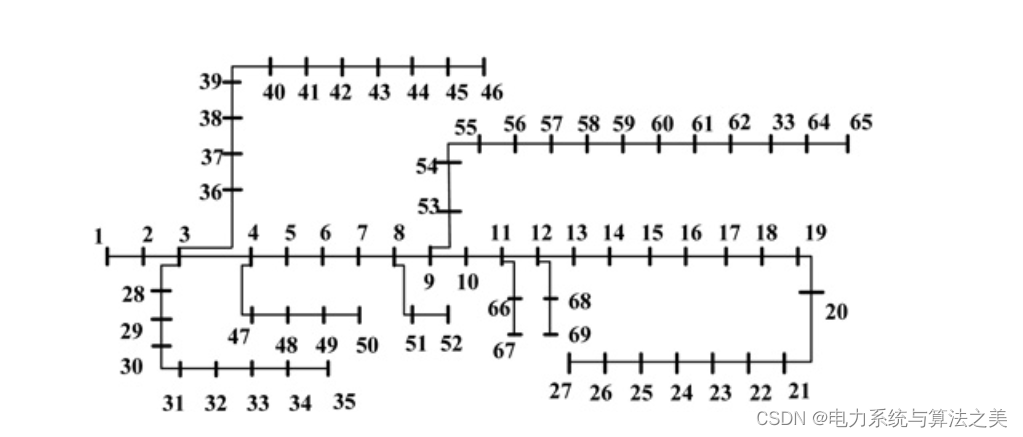
图4 69节点测试配电系统
3.1 33 节点测试配电系统的仿真
本节将在以下两种情况下考虑两种不同的DG运行模式。
3.1.1 情景1:DG运行的统一功率因数模式。
在这种情况下,假设DG产生有功功率,而不产生/消耗无功功率。使用建议的方法在网络中分配不同数量的DG。在表1中,建议的方法与其他方法进行了比较,即损失敏感系数(LSF)、改进的分析法(IA)和穷举负载流(ELF)方法[33]。从表1中可以看出,所提出的方法在降低损耗方面比其他方法有更好的表现。在放置一个DG的情况下,在这四种算法中,有三种算法建议在母线6上安装DG。为了显示建议的方法在寻找安装在母线6的DG的最佳发电量方面的性能,计算了网络损耗与安装在母线6的DG的发电量,如图5所示。如图5所示,如果安装在母线6上的DG产生2.706兆伏安,则损失达到最小值(0.09922兆瓦)。如表 1 所示,建议的方法找到了这个功率值,即安装在母线 6 上的 DG 应该产生的功率,以使损耗最小。
表 1 第一种场景的仿真结果(33节点测试配电系统)
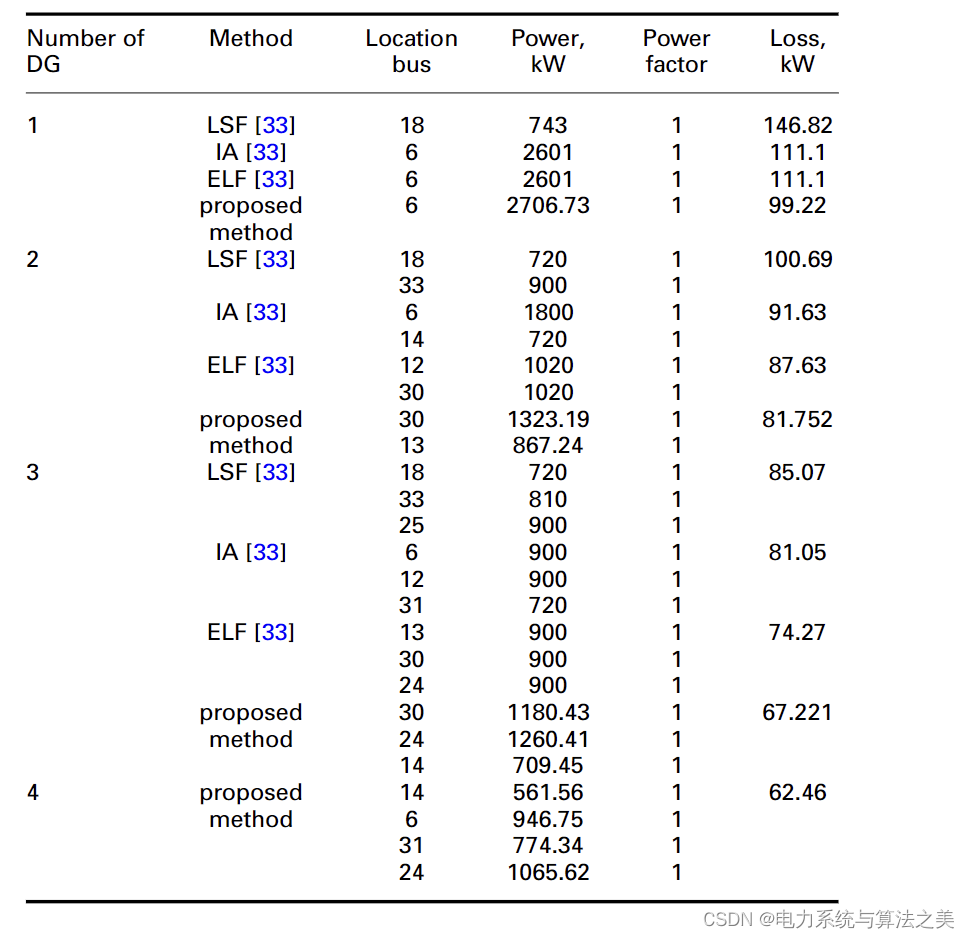
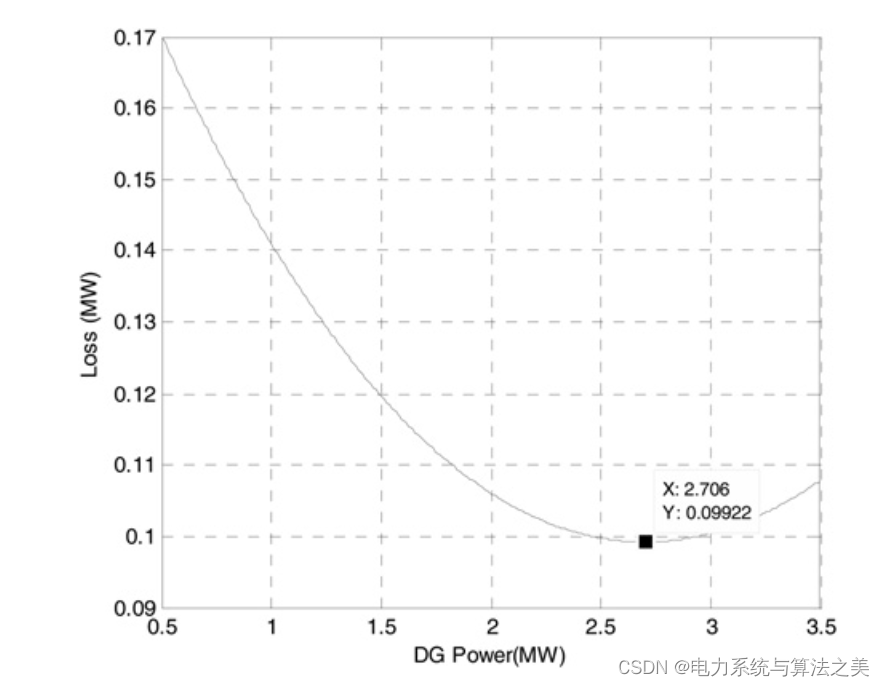
图5 发电量的网络损耗(DG安装在 6节点)
3.1.2 情景二:非统一功率因数的DG运行模式。
在这种情况下,假设DG的功率因数不一定等于1,仿真结果见表2。从表2中可以看出,建议的方法达到了最低的网络损耗。
在放置一个 DG 的情况下,建议的算法建议安装在母线 30。安装的 DG 的功率为 1844.85 kVA,滞后功率因数为 0.767。图 6 显示了损耗与 DG 位置及其功率因数的关系。如图所示,解析法和遗传算法相结合,通过在母线 30 上安装一台 DG(图 7)以 0.767 的滞后功率因数,达到了最小的网络损耗。为了解析解决该问题,总线的电压不等式约束(即 Vmin < V bus < V max)不能包含在优化问题中。因此,在优化程序完成后,可以而且应该检查母线电压和线电流,以保证母线电压的不等式约束。表3列出了安装DG机组后33个总线系统的最低和最高电压.
表 2 场景二(33节点测试配电系统)的仿真结果

表3 安装DG后的33个节点测试配电系统的最低和最高电压
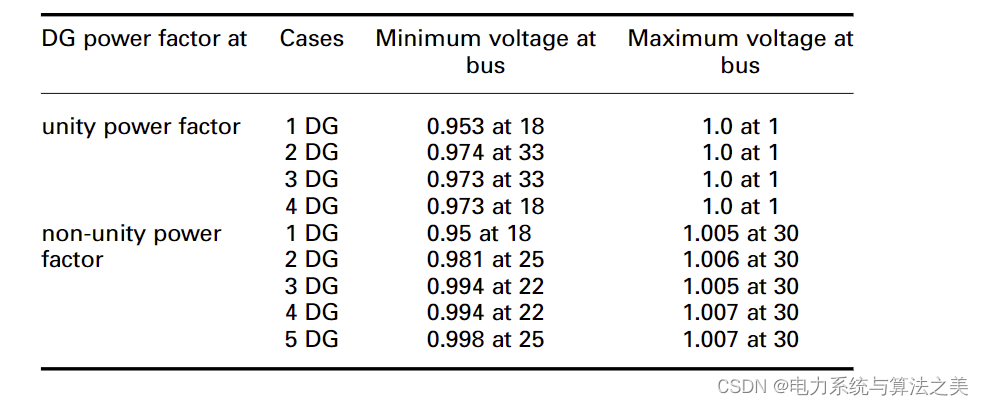
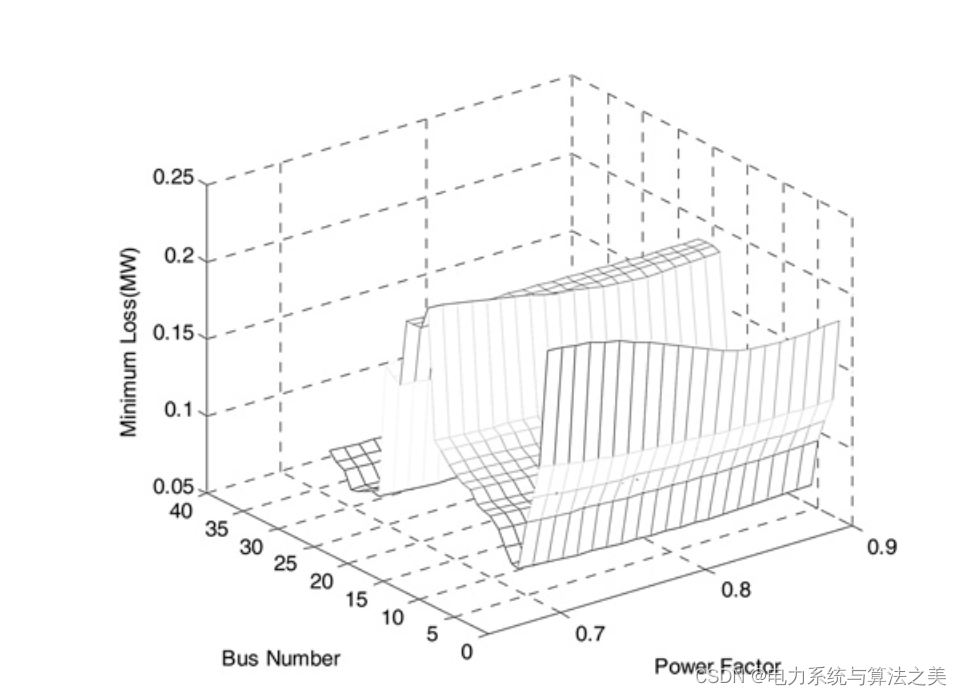
图 6 系统损耗与 DG 位置及其功率因数的关系

图7 在母线30安装一个DG,网络损失的最小值
3.2 69 节点测试配电系统仿真
本节对69 母线测试配电系统进行仿真。以下两种场景分别考虑了两种不同的 DG 运行模式。
3.2.1 场景一:DG 运行的单位功率因数模式:
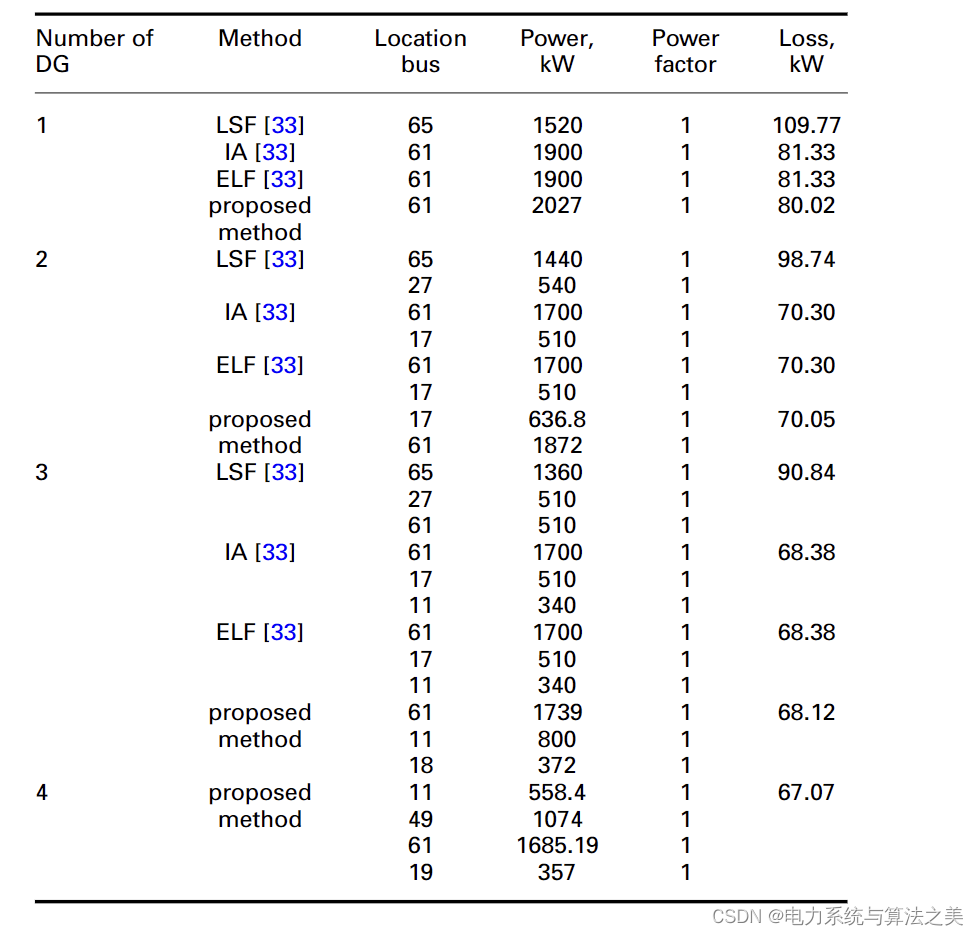
这种情况下,假设 DG 工作在单位功率因数模式,只能产生有功功率。 DG 分配的结果列于表 4。如表中所列,与其他方法相比,所提出的方法导致较低的网络损耗。
表 4 第一种场景(69节点测试配电系统)的仿真结果
3.2.2 场景二:DG 运行的非统一功率因数模式:
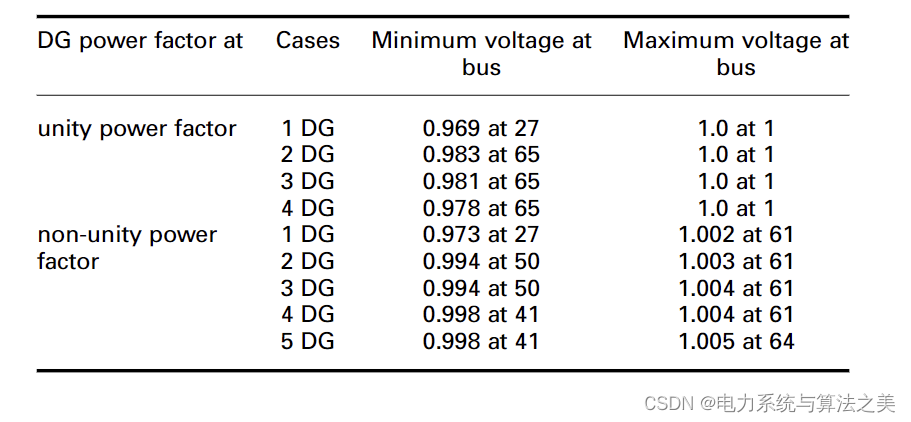
此时 DG 可以产生有功和无功功率,其功率因数不一定等于 1。69 年 DG 优化配置的结果母线测试配电系统见表 5。表 6 列出了 DG 机组安装后 69 母线系统的最小和最大电压。
表 5 场景二(69节点测试配电系统)的仿真结果
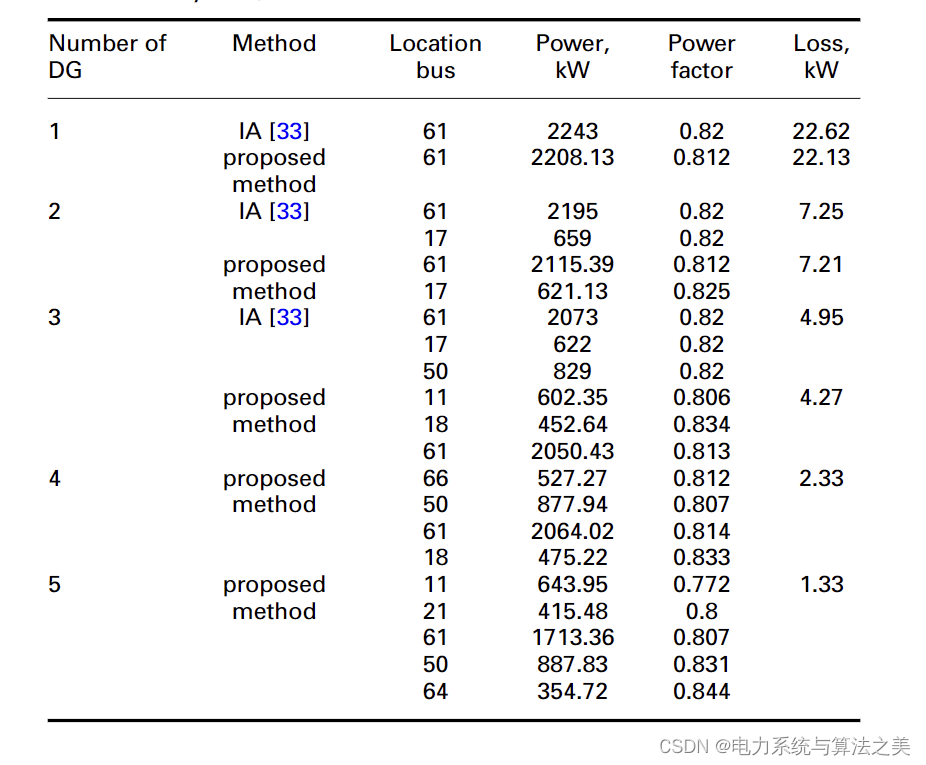
表 6 DG 安装后 69 母线测试配电系统的最小和最大电压
4 结论
本文提出了一种解析法和遗传算法相结合的方法,用于配电网多台分散发电机组的配置,使系统网损最小。该方法利用遗传算法来寻找分布式电源的最优安装位置,并使用一种新的解析公式来确定分布式电源容量。将该方法与IA、LSF和ELF方法在降低损耗方面进行了比较。结果表明,与其他方法相比,该方法达到了最低的损耗。
相关文章:

基于解析法和遗传算法相结合的配电网多台分布式电源降损配置(Matlab实现)
目录 1 概述 2 数学模型 2.1 问题表述 2.2 DG的最佳位置和容量(解析法) 2.3 使用 GA 进行最佳功率因数确定和 DG 分配 3 仿真结果与讨论 3.1 33 节点测试配电系统的仿真 3.2 69 节点测试配电系统仿真 4 结论 1 概述 为了使系统网损达到最低值&a…...

07mysql查询语句之子查询
#1.查询和Zlotkey相同部门的员工姓名和工资 SELECT last_name,salary FROM employees WHERE department_id IN ( SELECT department_id FROM employees WHERE last_name Zlotkey ); #2.查询工资比公司平均工资高的员工的员工号࿰…...
)
笙默考试管理系统-MyExamTest(22)
笙默考试管理系统-MyExamTest(22) 目录 一、 笙默考试管理系统-MyExamTest 二、 笙默考试管理系统-MyExamTest 三、 笙默考试管理系统-MyExamTest 四、 笙默考试管理系统-MyExamTest 五、 笙默考试管理系统-MyExamTest 笙默考试管理系统-MyExa…...
Windows 不同方式打开的cmd/dos窗口属性配置不同
文章目录 1. 默认值(控制台窗口)属性2. "C:\Windows\System32\cmd.exe" 属性3. "命令提示符"属性4. 自定义某标题cmd窗口属性5. cmd快捷方式的属性总结 最近在写某个批处理脚本时,意外发现 Windows系统中,在不…...

性能优化-webpack配置gzip
3步搞定,实测1.3Mjs压缩到363k,体积减少70% 1.装包 yarn add compression-webpack-plugin --dev 2.配置webpack 打开config/webpack.config.js 1)在 module.exports 导出函数前面引入插件 // gzip插件 const CompressionPlugin require(&qu…...

RabbitMQ 教程 | 第3章 客户端开发向导
👨🏻💻 热爱摄影的程序员 👨🏻🎨 喜欢编码的设计师 🧕🏻 擅长设计的剪辑师 🧑🏻🏫 一位高冷无情的编码爱好者 大家好,我是 DevO…...
基于深度学习的CCPD车牌检测系统(PyTorch+Pyside6+YOLOv5模型)
摘要:基于CCPD数据集的高精度车牌检测系统可用于日常生活中检测与定位车牌目标,利用深度学习算法可实现图片、视频、摄像头等方式的车牌目标检测识别,另外支持结果可视化与图片或视频检测结果的导出。本系统采用YOLOv5目标检测模型训练数据集…...

input元素中的form属性有什么用?
在HTML中,input元素的form属性用于指定该输入字段所属的表单(form元素)。通过将input元素的form属性设置为相应的表单的id值,可以将输入字段与表单进行关联。 这个属性对于两个主要目的非常有用: 表单关联࿱…...

【数据结构篇C++实现】- 特殊的线性表 - 串
友情链接:C/C系列系统学习目录 文章目录 串🚀一、串的定义🚀二、串的存储结构🛴(一)串的顺序存储结构1、定长顺序存储表示2、堆分配存储表示 🛴(二)串的链式存储结构3、块…...

DevOps系列文章 之 Springboot单元测试
在没有代码生成工具或尝试一门新的 ORM框架时,当我们希望不去另外写 Service 和 Controller 来验证 DAO 层的代码不希望只通过接口请求的方式来验证时,这时候单元测试的方式就可以帮助我们满足这一需求。 在我们开发Web应用时,经常会直接去观…...
04 linux之C 语言高级编程
gcc和gdb GNU工具 编译工具:把一个源程序编译为一个可执行程序调试工具:能对执行程序进行源码或汇编级调试软件工程工具:用于协助多人开发或大型软件项目的管理,如make、CVS、Subvision其他工具:用于把多个目标文件链…...

深入学习 Redis - Stream、Geospatial、HyperLogLog、Bitmap、Bitfields 类型扩展
目录 前言 Stream geospatial HyperLogLog Bitmaps Bitfields 前言 redis 中最关键的五个数据类型 String、List、Hash、Set、Zset 应用最广泛,同时 redis 也推出了额外的 5 个数据类型,他们分别是针对特殊场景才进行的应用的. Ps:这几种…...

Windows11+Opencv+Clion编译源码
Windows11OpencvClion编译源码 参考:https://www.robotsfan.com/posts/69395e08.html 注意事项 编译过程中使用的软件,开源码等所有工具的安装路径一定不要有中文和空格。cmake过程会下载一些文件,如果是局域网的话可能下载不下来…...
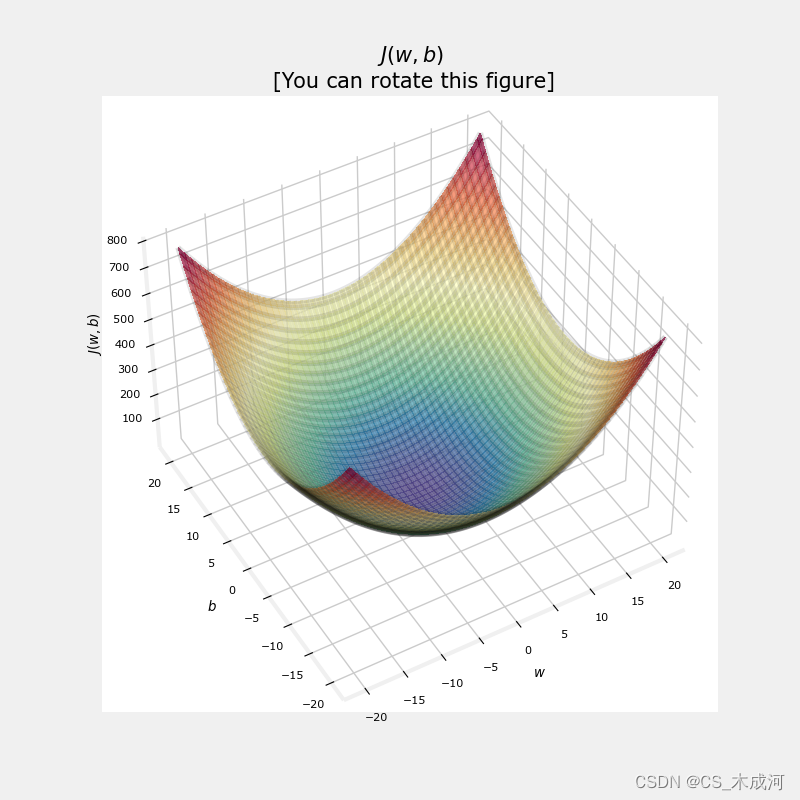
【机器学习】Cost Function
Cost Function 1、计算 cost2、cost 函数的直观理解3、cost 可视化总结附录 首先,导入所需的库: import numpy as np %matplotlib widget import matplotlib.pyplot as plt from lab_utils_uni import plt_intuition, plt_stationary, plt_update_onclic…...
【黑马头条之内容安全第三方接口】
本笔记内容为黑马头条项目的文本-图片内容审核接口部分 目录 一、概述 二、准备工作 三、文本内容审核接口 四、图片审核接口 五、项目集成 一、概述 内容安全是识别服务,支持对图片、视频、文本、语音等对象进行多样化场景检测,有效降低内容违规风…...

回归预测 | MATLAB实现GRNN广义回归神经网络多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现GRNN广义回归神经网络多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现GRNN广义回归神经网络多输入单输出回归预测(多指标,多图)效果一览基本介绍程序设计参考资料效果一览 基本介绍 MATLAB实现GRNN广义回归神经网络多输入单输出回归…...
详解)
STM32 HAL库函数——HAL_UART_RxCpltCallback()详解
HAL_UART_RxCpltCallback函数 他是谁,他和谁有关功能用法每收到一个字符,就自动调用一次??示例----接收未知长度的字符 他是谁,他和谁有关 HAL_UART_RxCpltCallback 是一个回调函数,用于在使用 HAL 库进行…...
前端调用合约如何避免出现transaction fail
前言: 作为开发,你一定经历过调用合约的时候发现 gas fee 超出限制,但是不知道报了什么错。这个时候一般都是触发了require错误合约校验。对于用户来说他不理解为什么一笔交易会花费如此大的gas,那我们作为开发如何尽量避免这种情…...

选择器的使用
目录 层级选择器属性选择器伪类选择器结构伪类选择器目标伪类选择器 层级选择器 /*子代选择器:选出box下的所有li标签*/.box>li{background-color: aliceblue;}/* 选出box后面的第一个兄弟li标签 */.boxli{background-color: aliceblue;}/* 选出box后面的所有兄…...

软考A计划-系统集成项目管理工程师-项目干系人管理-上
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例点击跳转>软考全系列点击跳转>蓝桥系列 👉关于作者 专注于Android/Unity和各种游…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
