【机器学习】Classification using Logistic Regression
Classification using Logistic Regression
- 1. 分类问题
- 2. 线性回归方法
- 3. 逻辑函数(sigmod)
- 4.逻辑回归
- 5. 决策边界
- 5.1 数据集
- 5.2 数据绘图
- 5.3 逻辑回归与决策边界的刷新
- 5.4 绘制决策边界
导入所需的库
import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_common import dlc, plot_data, draw_vthresh, sigmoid
from plt_one_addpt_onclick import plt_one_addpt_onclick
plt.style.use('./deeplearning.mplstyle')
1. 分类问题
分类问题的例子包括:将电子邮件识别为垃圾邮件或非垃圾邮件,或者确定肿瘤是恶性还是良性。这些都是二分类的例子,其中有两种可能的结果。结果可以用 ‘positive’/‘negative’ 成对描述,如’yes’/'no, ‘true’/‘false’ 或者 ‘1’/‘0’.
分类数据集的绘图通常使用符号来表示示例的结果。在下图中,“X”表示positive值,而“O”表示negative值。
x_train = np.array([0., 1, 2, 3, 4, 5])
y_train = np.array([0, 0, 0, 1, 1, 1])
X_train2 = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])
y_train2 = np.array([0, 0, 0, 1, 1, 1])
pos = y_train == 1
neg = y_train == 0fig,ax = plt.subplots(1,2,figsize=(8,3))
#plot 1, single variable
ax[0].scatter(x_train[pos], y_train[pos], marker='x', s=80, c = 'red', label="y=1")
ax[0].scatter(x_train[neg], y_train[neg], marker='o', s=100, label="y=0", facecolors='none', edgecolors=dlc["dlblue"],lw=3)ax[0].set_ylim(-0.08,1.1)
ax[0].set_ylabel('y', fontsize=12)
ax[0].set_xlabel('x', fontsize=12)
ax[0].set_title('one variable plot')
ax[0].legend()#plot 2, two variables
plot_data(X_train2, y_train2, ax[1])
ax[1].axis([0, 4, 0, 4])
ax[1].set_ylabel('$x_1$', fontsize=12)
ax[1].set_xlabel('$x_0$', fontsize=12)
ax[1].set_title('two variable plot')
ax[1].legend()
plt.tight_layout()
plt.show()
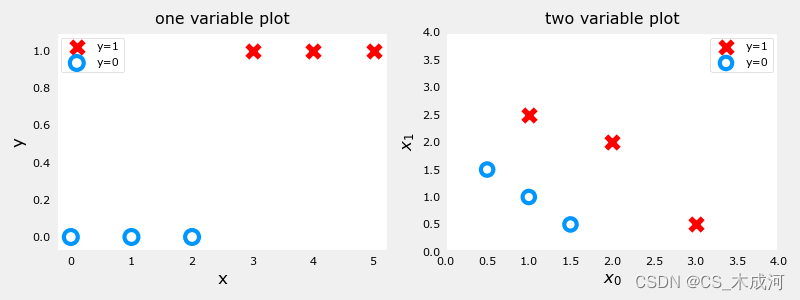
由上图可以看到,在单变量图中,positive显示为红色,y=1;negative显示为蓝色,y=0。在线性回归中,y的值不局限于两个值,可以是任意值。在多变量图中,同样地,positive显示为红色,negative显示为蓝色。在具有多个变量的线性回归的情况下,y不会被限制为两个值,类似的图将是三维的。
2. 线性回归方法
这里,我们使用前面介绍的线性回归模型根据肿瘤大小预测肿瘤是良性还是恶性。
w_in = np.zeros((1))
b_in = 0
plt.close('all')
addpt = plt_one_addpt_onclick( x_train,y_train, w_in, b_in, logistic=False)
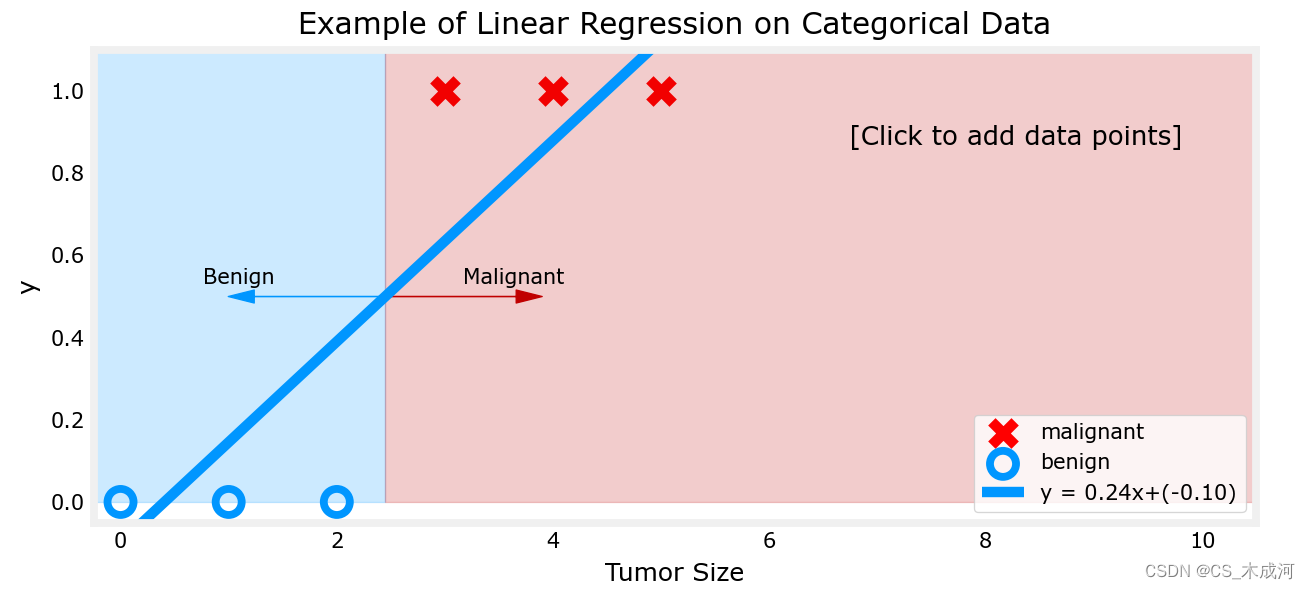
其中,阈值为0.5
现在,在大肿瘤大小范围(接近10)的最右侧添加更多的“恶性”数据点,并重新运行线性回归。
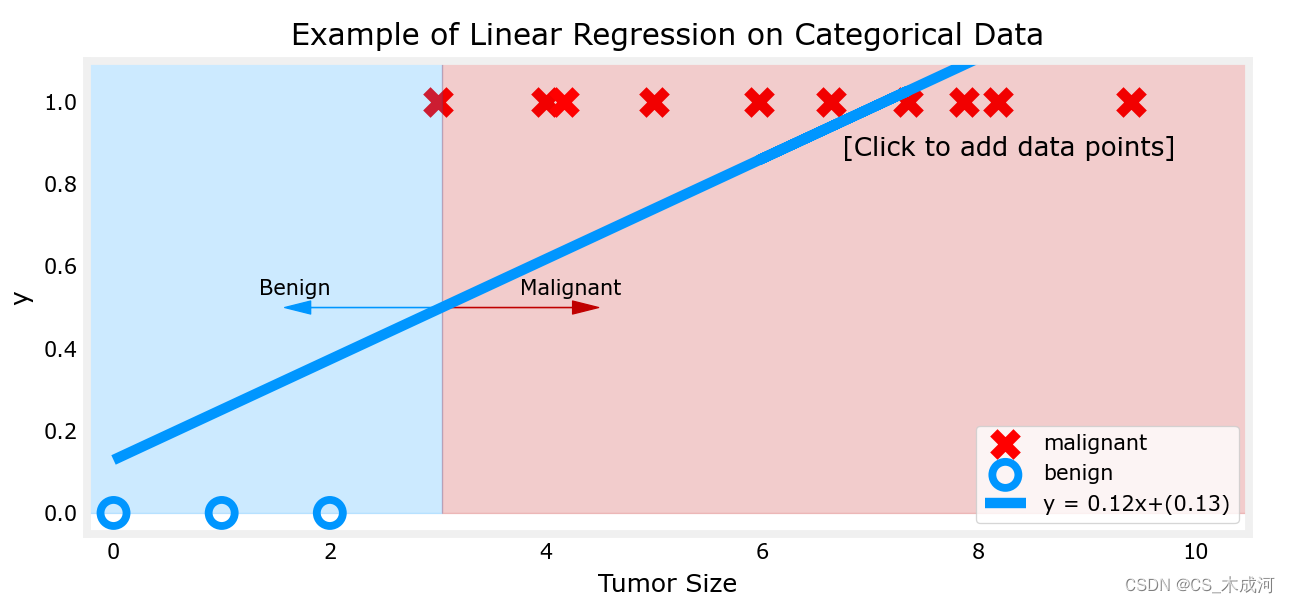
该模型预测了更大的肿瘤,但x=3的数据点被错误地预测了。
上面的例子表明,线性模型不足以对分类数据进行建模。
3. 逻辑函数(sigmod)
sigmod函数公式表示为:
g ( z ) = 1 1 + e − z (1) g(z) = \frac{1}{1+e^{-z}} \tag{1} g(z)=1+e−z1(1)
其中, z z z 是sigmod函数的输入,一个线性回归模型的输出。在单变量线性回归中,它是标量;在多变量线性回归中,它可能是包含 m m m个值的向量。
sigmoid函数的实现如下:
def sigmoid(z):"""Compute the sigmoid of zArgs:z (ndarray): A scalar, numpy array of any size.Returns:g (ndarray): sigmoid(z), with the same shape as z"""g = 1/(1+np.exp(-z))return g
对于输入变量 z z z,输出结果为:
# Generate an array of evenly spaced values between -10 and 10
z_tmp = np.arange(-10,11)# Use the function implemented above to get the sigmoid values
y = sigmoid(z_tmp)# Code for pretty printing the two arrays next to each other
np.set_printoptions(precision=3)
print("Input (z), Output (sigmoid(z))")
print(np.c_[z_tmp, y])
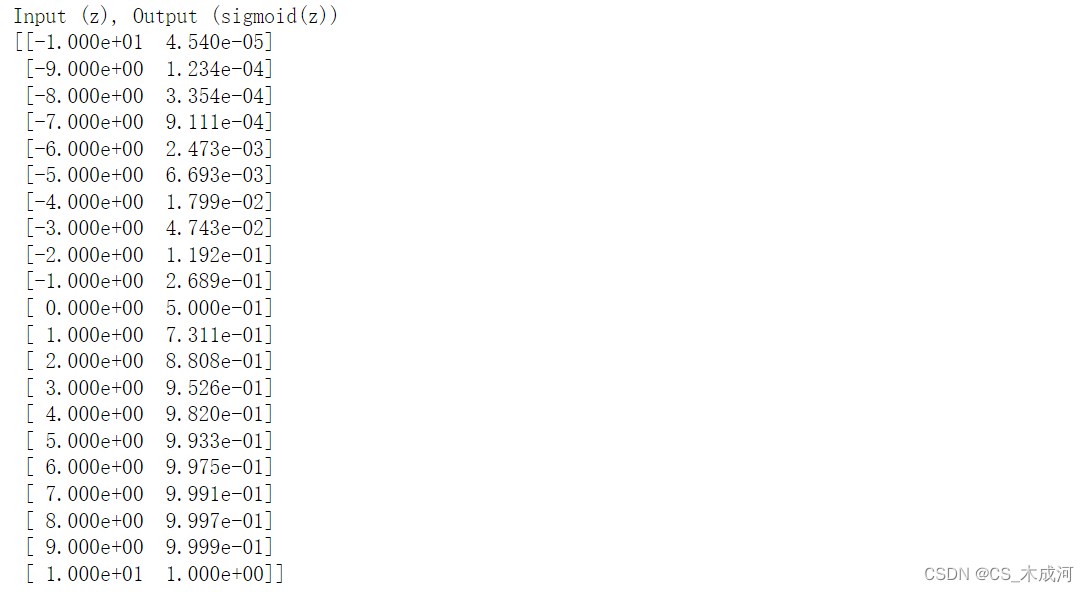
左边是输入z,右边是输出sigmod(z).输入值的范围从-10到10,输出值的范围从0到1.
对结果进行可视化:
# Plot z vs sigmoid(z)
fig,ax = plt.subplots(1,1,figsize=(5,3))
ax.plot(z_tmp, y, c="b")ax.set_title("Sigmoid function")
ax.set_ylabel('sigmoid(z)')
ax.set_xlabel('z')
draw_vthresh(ax,0)
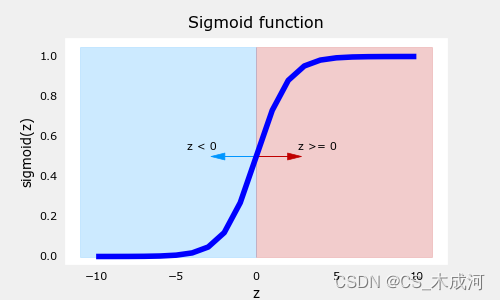
从图中可以看出,sigmod函数在z取小负数时趋近于0,在z取大正数时趋近于1.
4.逻辑回归
逻辑回归模型将sigmod函数应用到线性回归模型中,如下所示:
f w , b ( x ( i ) ) = g ( w ⋅ x ( i ) + b ) (2) f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = g(\mathbf{w} \cdot \mathbf{x}^{(i)} + b ) \tag{2} fw,b(x(i))=g(w⋅x(i)+b)(2)
其中,
g ( z ) = 1 1 + e − z (3) g(z) = \frac{1}{1+e^{-z}}\tag{3} g(z)=1+e−z1(3)
将逻辑回归应用到肿瘤分类的例子中。
首先,加载样例和初始化参数。
x_train = np.array([0., 1, 2, 3, 4, 5])
y_train = np.array([0, 0, 0, 1, 1, 1])w_in = np.zeros((1))
b_in = 0
plt.close('all')
addpt = plt_one_addpt_onclick( x_train,y_train, w_in, b_in, logistic=True)
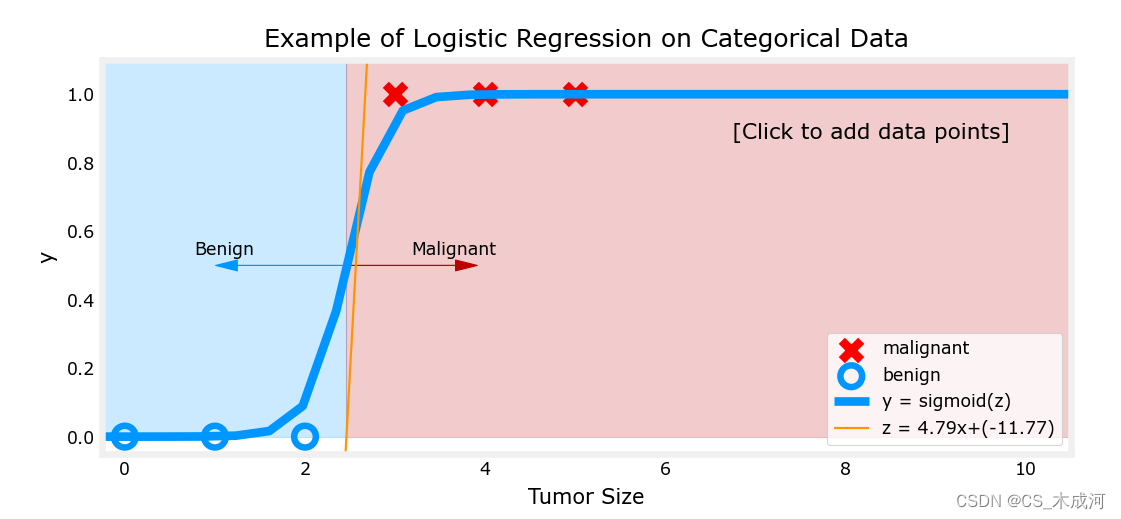
其中,橘黄色线是 ‘ z z z’ 或者 w ⋅ x ( i ) + b \mathbf{w} \cdot \mathbf{x}^{(i)} + b w⋅x(i)+b ,阈值为0.5
现在,在大肿瘤大小范围(接近10)中添加更多的数据点,并重新运行。
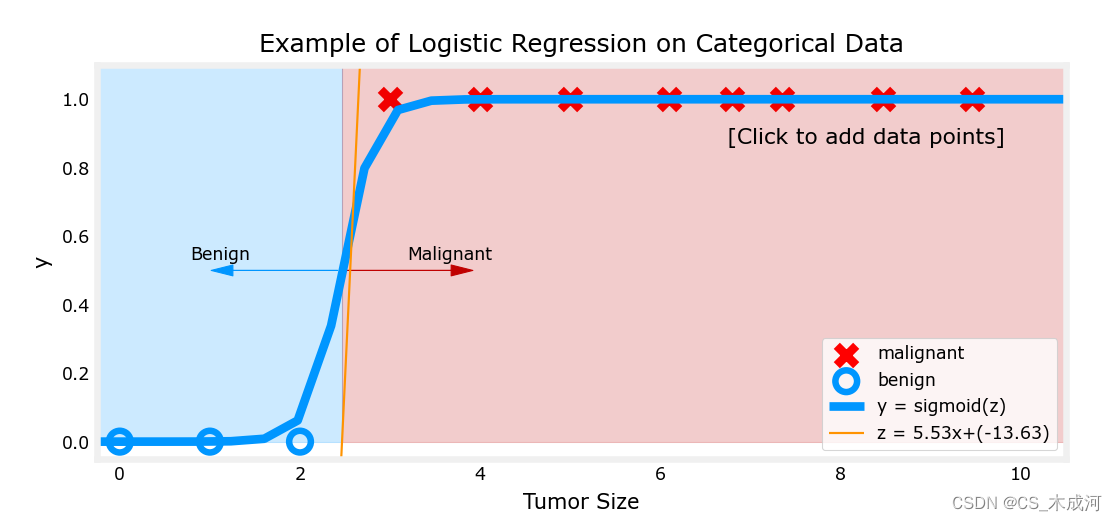
与线性回归模型不同,该模型继续做出正确的预测。
5. 决策边界
5.1 数据集
X = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])
y = np.array([0, 0, 0, 1, 1, 1]).reshape(-1,1)
5.2 数据绘图
fig,ax = plt.subplots(1,1,figsize=(4,4))
plot_data(X, y, ax)ax.axis([0, 4, 0, 3.5])
ax.set_ylabel('$x_1$')
ax.set_xlabel('$x_0$')
plt.show()
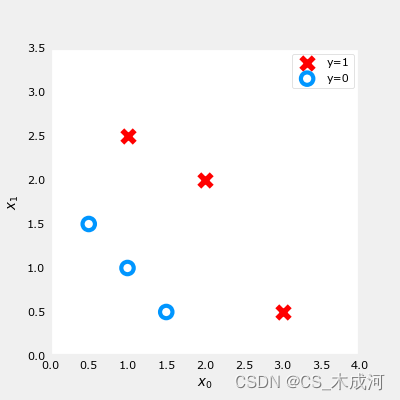
我们要根据数据集训练一个逻辑回归模型,其公式为: f ( x ) = g ( w 0 x 0 + w 1 x 1 + b ) f(x) = g(w_0x_0+w_1x_1 + b) f(x)=g(w0x0+w1x1+b),其中 g ( z ) = 1 1 + e − z g(z) = \frac{1}{1+e^{-z}} g(z)=1+e−z1, 训练好模型得到参数 b = − 3 , w 0 = 1 , w 1 = 1 b = -3, w_0 = 1, w_1 = 1 b=−3,w0=1,w1=1. 即 f ( x ) = g ( x 0 + x 1 − 3 ) f(x) = g(x_0+x_1-3) f(x)=g(x0+x1−3)。下面通过绘制决策边界来了解这个经过训练的模型在预测什么。
5.3 逻辑回归与决策边界的刷新
-
逻辑回归模型表示为:
f w , b ( x ( i ) ) = g ( w ⋅ x ( i ) + b ) (1) f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = g(\mathbf{w} \cdot \mathbf{x}^{(i)} + b) \tag{1} fw,b(x(i))=g(w⋅x(i)+b)(1)其中, g ( z ) g(z) g(z) 是 sigmoid 函数,它可以将所有值映射到0到1之间:
g ( z ) = 1 1 + e − z (2) g(z) = \frac{1}{1+e^{-z}}\tag{2} g(z)=1+e−z1(2)
w ⋅ x \mathbf{w} \cdot \mathbf{x} w⋅x 是向量点积运算:
w ⋅ x = w 0 x 0 + w 1 x 1 \mathbf{w} \cdot \mathbf{x} = w_0 x_0 + w_1 x_1 w⋅x=w0x0+w1x1 -
我们把模型的输出( f w , b ( x ) f_{\mathbf{w},b}(x) fw,b(x)) 解释为给定 x x x 并由 w w w和 b b b参数化的 y = 1 y=1 y=1 的概率.
-
这样, 为了从逻辑回归模型中获得最终预测 ( y = 0 y=0 y=0 or y = 1 y=1 y=1) , 使用以下启发式:
if f w , b ( x ) > = 0.5 f_{\mathbf{w},b}(x) >= 0.5 fw,b(x)>=0.5, predict y = 1 y=1 y=1
if f w , b ( x ) < 0.5 f_{\mathbf{w},b}(x) < 0.5 fw,b(x)<0.5, predict y = 0 y=0 y=0
-
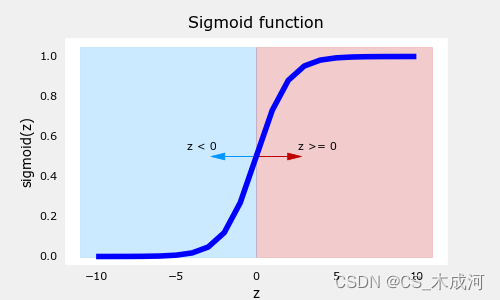
绘制sigmoid 函数来看看哪里 g ( z ) > = 0.5 g(z) >= 0.5 g(z)>=0.5
# Plot sigmoid(z) over a range of values from -10 to 10
z = np.arange(-10,11)fig,ax = plt.subplots(1,1,figsize=(5,3))
# Plot z vs sigmoid(z)
ax.plot(z, sigmoid(z), c="b")ax.set_title("Sigmoid function")
ax.set_ylabel('sigmoid(z)')
ax.set_xlabel('z')
draw_vthresh(ax,0)
-
如图所示,当 z > = 0 z >=0 z>=0 时, g ( z ) > = 0.5 g(z) >= 0.5 g(z)>=0.5
-
对于逻辑回归模型, z = w ⋅ x + b z = \mathbf{w} \cdot \mathbf{x} + b z=w⋅x+b. 因此,
if w ⋅ x + b > = 0 \mathbf{w} \cdot \mathbf{x} + b >= 0 w⋅x+b>=0, 模型预测 y = 1 y=1 y=1
if w ⋅ x + b < 0 \mathbf{w} \cdot \mathbf{x} + b < 0 w⋅x+b<0, 模型预测 y = 0 y=0 y=0
5.4 绘制决策边界
现在,我们回到例子中理解逻辑回归模型是如何预测的.
- 我们的逻辑回归模型为:
f ( x ) = g ( − 3 + x 0 + x 1 ) f(x) = g(-3 + x_0+x_1) f(x)=g(−3+x0+x1) - 从上面所讲,可以知道 if − 3 + x 0 + x 1 > = 0 -3 + x_0+x_1 >= 0 −3+x0+x1>=0,模型预测 y = 1 y=1 y=1
通过绘图来可视化。从绘制 − 3 + x 0 + x 1 = 0 -3+x_0+x_1=0 −3+x0+x1=0开始,这相当于 x 1 = 3 − x 0 x_1=3-x_0 x1=3−x0。
# Choose values between 0 and 6
x0 = np.arange(0,6)x1 = 3 - x0
fig,ax = plt.subplots(1,1,figsize=(5,4))
# Plot the decision boundary
ax.plot(x0,x1, c="b")
ax.axis([0, 4, 0, 3.5])# Fill the region below the line
ax.fill_between(x0,x1, alpha=0.2)# Plot the original data
plot_data(X,y,ax)
ax.set_ylabel(r'$x_1$')
ax.set_xlabel(r'$x_0$')
plt.show()
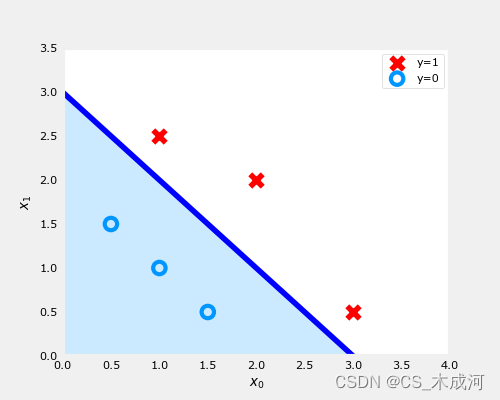
-
在上图中,蓝线表示 x 0 + x 1 − 3 = 0 x_0+x_1-3=0 x0+x1−3=0,它应该在3处与 x 1 x_1 x1轴相交(如果我们设置 x 1 x_1 x1=3, x 0 x_0 x0=0),并且在3处相交 x 0 x_0 x0轴(如果我们将 x 1 x_1 x1设置为0, x 0 x_0 x0=3)。
-
阴影区域表示 − 3 + x 0 + x 1 < 0 -3+x_0+x_1<0 −3+x0+x1<0。该线上方的区域为 − 3 + x 0 + x 1 > 0 -3+x_0+x_1>0 −3+x0+x1>0。
-
阴影区域(线下)中的任何点都被分类为 y = 0 y=0 y=0。该线上或上方的任何点都被分类为 y = 1 y=1 y=1。这条线被称为“决策边界”。
通过使用高阶多项式项(例如: f ( x ) = g ( x 0 2 + x 1 − 1 ) f(x) = g( x_0^2 + x_1 -1) f(x)=g(x02+x1−1)),我们可以得出更复杂的非线性边界。
相关文章:

【机器学习】Classification using Logistic Regression
Classification using Logistic Regression 1. 分类问题2. 线性回归方法3. 逻辑函数(sigmod)4.逻辑回归5. 决策边界5.1 数据集5.2 数据绘图5.3 逻辑回归与决策边界的刷新5.4 绘制决策边界 导入所需的库 import numpy as np %matplotlib widget import m…...

全方位支持图文和音视频、100+增强功能,Facebook开源数据增强库AugLy
Facebook 近日开源了数据增强库 AugLy,包含四个子库,每个子库对应不同的模态,每个库遵循相同的接口。支持四种模态:文本、图像、音频和视频。 最近,Facebook 开源了一个新的 Python 库——AugLy,该库旨在帮…...
RxSwift 使用方式
背景 最近项目业务,所有模块已经支持Swift混编开发,正在逐步使用Swift 方式进行开发新业务,以及逐步替换老业务方式进行发展,所以使用一些较为成熟的Swift 的三方库,成为必要性,经过调研发现RxSwift 在使用…...

HTML5 Web Worker
HTML5 Web Worker是一种浏览器提供的JavaScript多线程解决方案,它允许在后台运行独立于页面主线程的脚本,从而避免阻塞页面的交互和渲染。Web Worker可以用于执行计算密集型任务、处理大量数据、实现并行计算等,从而提升前端应用的性能和响应…...

25.9 matlab里面的10中优化方法介绍—— 惩罚函数法求约束最优化问题(matlab程序)
1.简述 一、算法原理 1、问题引入 之前我们了解过的算法大部分都是无约束优化问题,其算法有:黄金分割法,牛顿法,拟牛顿法,共轭梯度法,单纯性法等。但在实际工程问题中,大多数优化问题都属于有约…...

django channels实战(websocket底层原理和案例)
1、websocket相关 1.1、轮询 1.2、长轮询 1.3、websocket 1.3.1、websocket原理 1.3.2、django框架 asgi.py在django项目同名app目录下 1.3.3、聊天室 django代码总结 小结 1.3.4、群聊(一) 前端代码 后端代码 1.3.5、群聊(二)…...
学习使用axios,绑定动态数据
目录 axios特性 案例一:通过axios获取笑话 案例二:调用城市天气api接口数据实现天气查询案例 axios特性 支持 Promise API 拦截请求和响应(可以在请求前及响应前做某些操作,例如,在请求前想要在这个请求头中加一些…...
c语言内存函数的深度解析
本章对 memcpy,memmove,memcmp 三个函数进行详解和模拟实现; 本章重点:3个常见内存函数的使用方法及注意事项并学会模拟实现; 如果您觉得文章不错,期待你的一键三连哦,你的鼓励是我创作的动力…...

低代码平台介绍(国内常见的)
文章目录 前言1、阿里云宜搭2、腾讯云微搭3、百度爱速搭4、华为云Astro轻应用 Astro Zero(AppCube)5、字节飞书多维表格6、云程低代码平台7、ClickPaaS8、网易轻舟9、用友YonBuilder10、金蝶苍穹云平台11、泛微平台12、蓝凌低代码平台13、简道云14、轻流…...
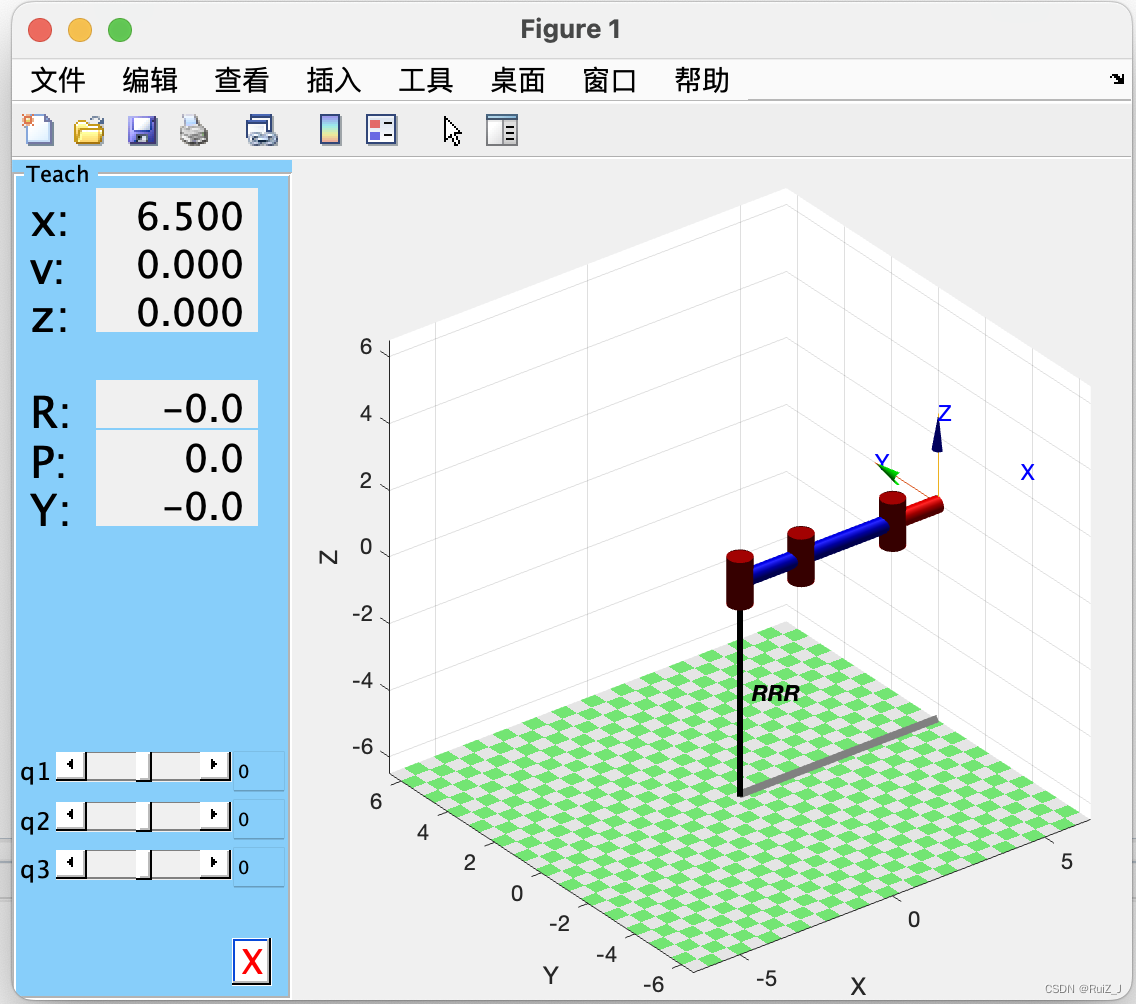
matlab RRR机械臂 简略代码
RRR机器人!启动! gazebo在arm mac上似乎难以运行,退而选择Matlab,完成老师第一个作业,现学现卖,权当记录作业过程,有不足之处,多多指教。 作业!启动! RRR机…...

集成测试,单元测试隔离 maven-surefire-plugin
详见 集成测试,单元测试隔离 maven-surefire-plugin maven的goal生命周期 Maven生存周期 - 含 integration-test Maven本身支持的命令(Goals)是有顺序的,越后面执行的命令,会将其前面的命令和其本身按顺序执行一遍,…...
渗透测试基础知识(1)
渗透基础知识一 一、Web架构1、了解Web2、Web技术架构3、Web客户端技术4、Web服务端组成5、动态网站工作过程6、后端存储 二、HTTP协议1、HTTP协议解析2、HTTP协议3、http1.1与http2.0的区别4、HTTP协议 三、HTTP请求1、发起HTTP请求2、HTTP响应与请求-HTTP请求3、HTTP响应与请…...

Android NDK开发
工程目录图 NDK中文官网 请点击下面工程名称,跳转到代码的仓库页面,将工程 下载下来 Demo Code 里有详细的注释 代码:TestNDK 参考文献 Android NDK 从入门到精通(汇总篇)Android JNI(一)——NDK与JNI基础Android之…...

使用python爬取淘宝商品信息
要使用Python爬取淘宝商品信息,您可以按照以下步骤: 安装必要的库 您需要安装Python的requests库和BeautifulSoup库。 要使用Python爬取淘宝商品信息,您可以按照以下步骤:安装必要的库 您需要安装Python的requests库和Beautifu…...
)
QEMU源码全解析18 —— QOM介绍(7)
接前一篇文章:QEMU源码全解析17 —— QOM介绍(6) 本文内容参考: 《趣谈Linux操作系统》 —— 刘超,极客时间 《QEMU/KVM》源码解析与应用 —— 李强,机械工业出版社 特此致谢! 上一回完成了对…...

【华为OD机试】 选修课
题目描述 现有两门选修课,每门选修课都有一部分学生选修,每个学生都有选修课的成绩,需要你找出同时选修了两门选修课的学生,先按照班级进行划分,班级编号小的先输出,每个班级按照两门选修课成绩和的降序排序…...

225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。 实现 MyStack 类: void push(int x) 将元素 x 压入栈顶。 int pop() 移除并返回栈顶元素。 int to…...
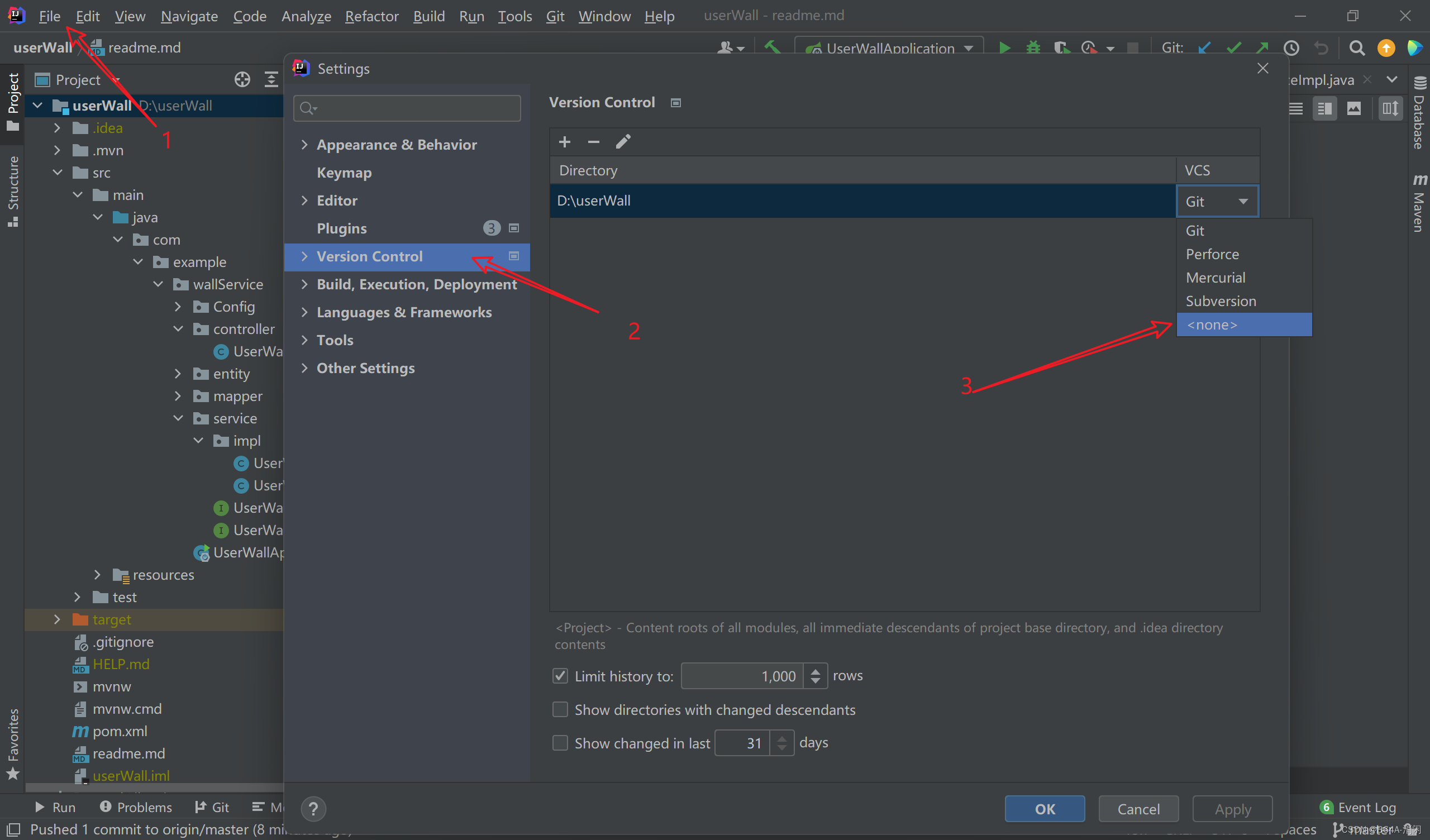
IDEA将本地项目上传到码云
一、创建本地仓库并关联 用IDEA打开项目,在菜单栏点击vcs->create git repository创建本地仓库, 选择当前项目所在的文件夹当作仓库目录。 二、将项目提交本地仓库 项目名右键就会出现“GIT”这个选项->Add->Commit Directory, 先将项目add…...
Ubuntu更改虚拟机网段(改成桥接模式无法连接网络)
因为工作需要,一开始在安装vmware和虚拟机时,是用的Nat网络。 现在需要修改虚拟机网段,把ip设置成和Windows端同一网段,我们就要去使用桥接模式。 环境: Windows10、Ubuntu20.04虚拟机编辑里打开虚拟网络编辑器&#…...
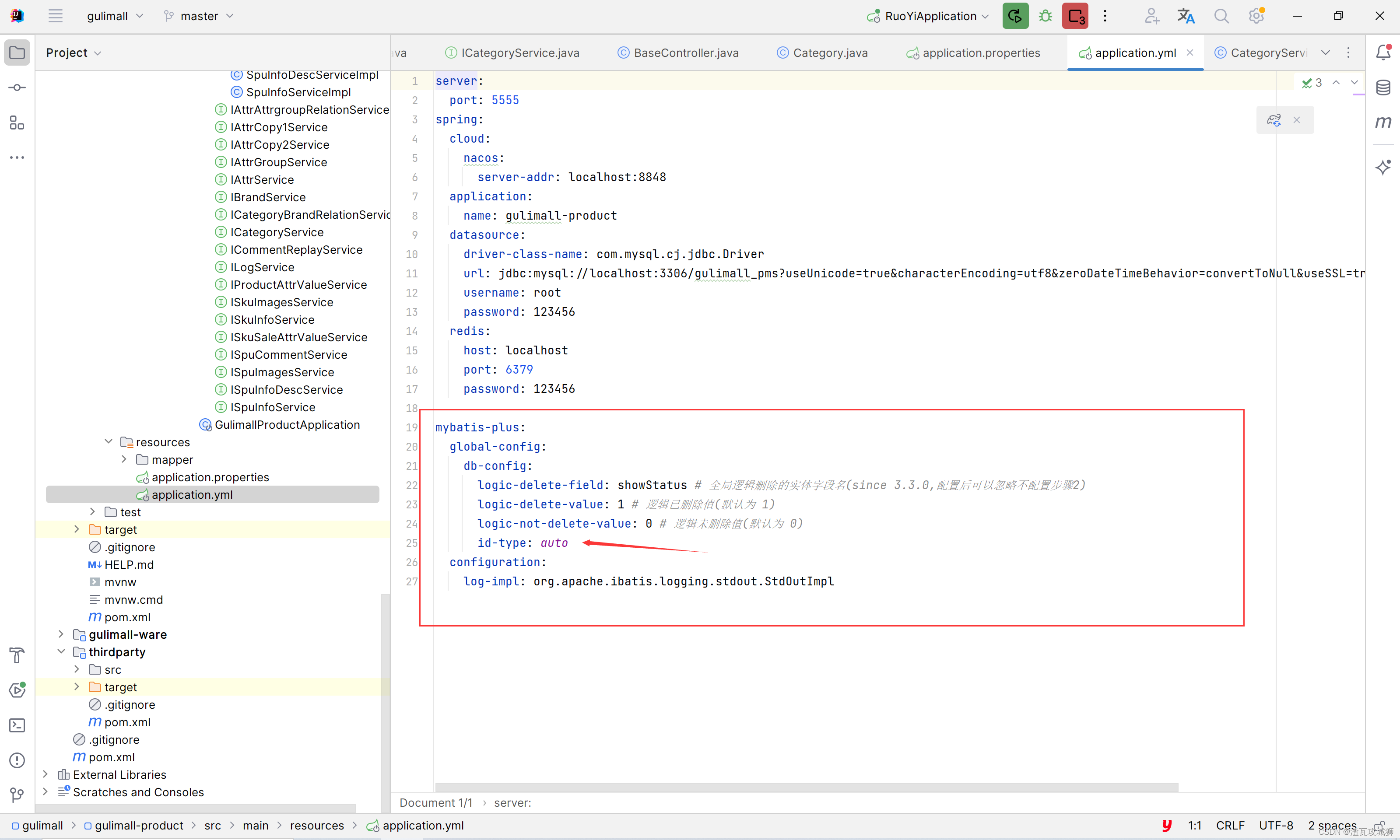
谷粒商城第七天-商品服务之分类管理下的删除、新增以及修改商品分类
目录 一、总述 1.1 前端思路 1.2 后端思路 二、前端部分 2.1 删除功能 2.2 新增功能 2.3 修改功能 三、后端部分 3.1 删除接口 3.2 新增接口 3.3 修改接口 四、总结 一、总述 1.1 前端思路 删除和新增以及修改的前端无非就是点击按钮,就向后端发送请求…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
