【计算复杂性理论】证明复杂性(八):命题鸽巢原理(Propositional Pigeonhole Principle)的指数级归结下界
往期文章:
- 【计算复杂性理论】证明复杂性(Proof Complexity)(一):简介
- 【计算复杂性理论】证明复杂性(二):归结(Resolution)与扩展归结(Extended Resolution)证明系统
- 【计算复杂性理论】证明复杂性(三):弗雷格(Frege)与扩展弗雷格(Extended Frege)证明系统
- 【计算复杂性理论】证明复杂性(四):相继式演算(Sequent Calculus)
- 【计算复杂性理论】证明复杂性(五):量化命题演算(Quantified Propositional Calculus)
- 【计算复杂性理论】证明复杂性(六):其他证明系统简介
- 【计算复杂性理论】证明复杂性(七):有界算术(Bounded Arithmetic)与IΔ₀理论
文章目录
- 一、命题鸽巢原理
- 二、定理的表述和证明的大体思路
- 二、关键赋值CTA
- 三、半零子句HZC
- 四、相邻的关键赋值
- 五、高复杂度子句
- 六、函数 f ( n ) f(n) f(n)
- 参考文献
1985年,Haken的论文[1]证明了归结证明系统在命题鸽巢原理上有指数级下界,即命题鸽巢原理不存在多项式大小的归结证明。这项发现说明了归结的强度非常弱,而且因为DPLL、CDCL算法对应的证明系统不强于归结,这也说明了DPLL、CDCL算法的时间复杂度是指数级别的。
关于文字、子句、合取范式等术语的定义请见【算法/图论】2-SAT问题详解。
我们规定:对于变量 v v v,子句 C C C如果包含文字 v v v,则称 v v v在 C C C中是以肯定的形式出现的;若包含文字 ¬ v \neg v ¬v,则称 v v v在 C C C中是以否定的形式出现的。
一、命题鸽巢原理
鸽巢原理(pigeonhole principle)是说,如果 n n n个鸽子要飞到 m m m个巢里面, n > m n>m n>m,且每个巢最多只能有一个鸽子,那么这一定是不可能的。在国内对应的叫法是抽屉原理。
命题鸽巢原理(propositional pigeonhole principle)就是鸽巢原理表示成命题公式的形式。这篇文章只讨论 m = n − 1 m=n-1 m=n−1,即巢比鸽子少一个的情况。定义变量 P i k ( 1 ≤ i ≤ n , 1 ≤ k ≤ n − 1 ) P_{ik}\ (1\le i\le n,1\le k\le n-1) Pik (1≤i≤n,1≤k≤n−1)表示编号为 i i i的鸽子飞进编号为 k k k的巢里。定义命题公式 P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1为下列公式的合取:
- P i 1 ∨ P i 2 ∨ ⋯ ∨ P i , n − 1 P_{i1}\lor P_{i2}\lor\cdots\lor P_{i,n-1} Pi1∨Pi2∨⋯∨Pi,n−1, 1 ≤ i ≤ n 1\le i\le n 1≤i≤n
- ¬ P i k ∨ ¬ P j k \neg P_{ik}\lor\neg P_{jk} ¬Pik∨¬Pjk, 1 ≤ i < j ≤ n 1\le i<j\le n 1≤i<j≤n, 1 ≤ k ≤ n − 1 1\le k\le n-1 1≤k≤n−1
P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1表示的就是 n n n个鸽子可以飞到 m m m个巢里面并且每个巢里只有不超过一个鸽子。第一条表示每个鸽子必须飞到至少一个巢里面;第二条表示任两个鸽子不能飞到同一个巢里面,这样就保证了每个巢里的鸽子数量小于 2 2 2。我们不必限制每个鸽子只能飞到一个巢里面,因为如果一个鸽子飞到超过一个巢里面了,其他鸽子的空间就更小了。显然, P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1是不可满足的(即 ¬ P H P n n − 1 \neg\mathrm{PHP}_{n}^{n-1} ¬PHPnn−1是永真式),而我们要讨论的就是用归结证明系统反驳 P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1的复杂性。
二、定理的表述和证明的大体思路
定理(Haken 1985[1]) 存在一个常数 c > 1 c>1 c>1,使得对于充分大的 n n n, P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1的任何归结反驳都包含至少 c n c^n cn个不同的子句。
证明思路:对于某个固定的 n n n,假设我们有 P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1的一个归结反驳 R R R。在接下来的证明中,我们令 k = ⌊ n − 1 4 ⌋ k=\left\lfloor\frac{n-1}{4}\right\rfloor k=⌊4n−1⌋。
我们可以把变量表示成表格的形式。每行对应同一只鸽子,每列对应同一个巢。比如 P H P 3 2 \mathrm{PHP}_{3}^{2} PHP32的变量表格如下:
| 鸽子\巢 | 1 1 1 | 2 2 2 |
|---|---|---|
| 1 1 1 | P 11 P_{11} P11 | P 12 P_{12} P12 |
| 2 2 2 | P 21 P_{21} P21 | P 22 P_{22} P22 |
| 3 3 3 | P 31 P_{31} P31 | P 32 P_{32} P32 |
定义 F S 1 \mathrm{FS}1 FS1是满足所有下列条件的集合:它包含 P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1的 k k k个变量,且没有两个变量在表格中处于同一行或同一列。令 h ( n ) h(n) h(n)是 F S 1 \mathrm{FS}1 FS1中的元素个数。对于 F S 1 \mathrm{FS}1 FS1中的每个变量集合 S S S,我们在 R R R中找到一个对应的“高复杂度子句”(highly complex clause, HCC)。我们定义一个函数 g ( n ) g(n) g(n)并证明任何一个高复杂度子句至多对应 F S 1 \mathrm{FS}1 FS1中的 g ( n ) g(n) g(n)个元素。因此, R R R中至少包含 f ( n ) = h ( n ) g ( n ) f(n)=\cfrac{h(n)}{g(n)} f(n)=g(n)h(n)个不同的子句。我们将会证明 f ( n ) f(n) f(n)是指数函数。∎
接下来,我们填补这个证明的详细内容。
二、关键赋值CTA
我们按如下方式定义关键赋值(critical truth assignment, CTA):考虑为变量表格的每一格赋 0 0 0和 1 1 1,如果除了某一行变量的赋值全为 0 0 0(称这一行为零行)外,其余格子的赋值满足:每一行恰有一个 1 1 1、每一列也恰有一个 1 1 1,那么称这个赋值为关键赋值。比如下面这个例子,鸽子的数量为 4 4 4,第三行为零行:
| 鸽子\巢 | 1 1 1 | 2 2 2 | 3 3 3 |
|---|---|---|---|
| 1 1 1 | 1 1 1 | 0 0 0 | 0 0 0 |
| 2 2 2 | 0 0 0 | 0 0 0 | 1 1 1 |
| 3 3 3 | 0 \color{red}0 0 | 0 \color{red}0 0 | 0 \color{red}0 0 |
| 4 4 4 | 0 0 0 | 1 1 1 | 0 0 0 |
实际上就是给除了第三只鸽子外的其他鸽子安排了合适的巢。关键赋值的含义就是舍弃其中一个鸽子,给其他鸽子分别找到一一对应的巢。关键赋值有 n ! n! n!个(舍弃一只鸽子有 n n n种方案,其他鸽子与巢一一对应有 ( n − 1 ) ! (n-1)! (n−1)!种方案)。令 C T A \mathcal{CT\!\!A} CTA为所有关键赋值的集合,每个关键赋值会使 P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1中的一个子句为假,那就是规定了零行对应的鸽子至少应该飞进一个巢的子句。上面这个例子中为假的子句就是 P 31 ∨ P 32 ∨ P 33 P_{31}\lor P_{32}\lor P_{33} P31∨P32∨P33。
如果一个关键赋值 V V V中第 r r r行 c c c列为 1 1 1,则称行 r r r和列 c c c关于 V V V相对应。零行不与任何列相对应。上面的例子中,行 1 1 1、 2 2 2、 3 3 3分别与列 1 1 1、 3 3 3、 2 2 2对应。
三、半零子句HZC
定义归结反驳 R R R中的半零子句(half zero clause, HZC)为任何满足下列条件的子句 C C C:存在某一行(称为关键行),使得 C C C包含这一行的恰好 2 k 2k 2k个变量,这 2 k 2k 2k个变量以肯定的形式出现在 C C C中。比如当 n = 5 n=5 n=5时, k = 1 k=1 k=1,那么 P 22 ∨ ¬ P 43 ∨ P 51 ∨ P 53 P_{22}\lor\neg P_{43}\lor P_{51}\lor P_{53} P22∨¬P43∨P51∨P53就是一个半零子句,第 5 5 5行是关键行。对于一个关键赋值 V V V和半零子句 C C C,如果 C C C的关键行就是 V V V的零行,而且 C C C在赋值 V V V下的取值为假,那么我们就称 C C C代表(present) V V V。我们令所有半零子句构成的集合为 H Z C \mathcal{HZC} HZC。
引理1 若 C C C代表 V V V,则 C C C在变量表格的每行和每列中至多有一个以否定的形式出现的变量;特别地, C C C的关键行没有以否定的形式出现的变量。
证明:只用证前半句话。由于 C C C是一个子句(即简单析取式),要让它为假,必须让其中每个文字的赋值为 0 0 0。显然, C C C中关键行的文字的赋值是为 0 0 0的;因此只需考虑非关键行。如果 P i k P_{ik} Pik在 V V V下的赋值为 0 0 0,那么该变量如果在 C C C中出现,要让 C C C不可满足, P i k P_{ik} Pik只能以肯定的形式出现。只有在 V V V下的赋值为 1 1 1的变量才能以否定的形式出现。而 V V V中每行、每列至多只有一个变量赋值为 1 1 1,因此 C C C在每行、每列至多有一个以否定的形式出现的变量。∎
引理2 每个关键赋值至少被一个半零子句代表。
证明:对于一个关键赋值 V V V,我们重点要证明一个归结反驳 R R R中必须出现一个能够代表 V V V的半零子句。令 q q q是 V V V的零行对应的鸽子的编号(即编号为 q q q个鸽子在赋值 V V V下是无家可归的)。这里会用到一个事实:如果子句 C , D C,D C,D归结的结果是 E E E,那么使 E E E为假的赋值必使 C C C或 D D D为假。这是因为, E E E是 C ∧ D C\land D C∧D的推论,使 C ∧ D C\land D C∧D为真的赋值必然使 E E E为真,而 E E E为假,所以 C ∧ D C\land D C∧D为假,即 C C C或 D D D为假。因此,如果关键赋值 V V V使某个子句 E E E为假,而 E E E又是 C , D C,D C,D归结得到的,那么 V V V必然使 C , D C,D C,D中的至少一个为假。由于空子句是 R R R的最后一个子句,关键赋值一定使空子句为假,故可以令 E E E为空子句。假设我们站在 E E E上,而 V V V使 C C C为假,那我们就跳到 C C C处;如果 C C C是 F , G F,G F,G归结而来而 V V V使 F F F为假,我们就跳到 F F F处;一直这样追根溯源,每次我们所到的子句在 V V V下的取值都为假,直到跳到 P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1的一个子句为止。根据引理1,这个子句必然是 P i 1 ∨ P i 2 ∨ ⋯ ∨ P i , n − 1 P_{i1}\lor P_{i2}\lor\cdots\lor P_{i,n-1} Pi1∨Pi2∨⋯∨Pi,n−1的形式(另一种子句一行有两个否定出现的变量,不可能在 V V V下赋值为假)。要让这种形式的子句为假,就要求其包含的变量的赋值全为 0 0 0。而 V V V只有第 q q q行赋值全为 0 0 0,所以这个子句一定是 P q 1 ∨ P q 2 ∨ ⋯ ∨ P q , n − 1 P_{q1}\lor P_{q2}\lor\cdots\lor P_{q,n-1} Pq1∨Pq2∨⋯∨Pq,n−1。现在考虑从 P q 1 ∨ P q 2 ∨ ⋯ ∨ P q , n − 1 P_{q1}\lor P_{q2}\lor\cdots\lor P_{q,n-1} Pq1∨Pq2∨⋯∨Pq,n−1到 E E E的归结路径。每次归结,子句中有一个变量被消除,同时可能有其他文字被加进来。对于第 q q q行,每次至多有一个变量被消除,同时可能有其他出现形式为肯定的变量加进来。第 q q q行永远不会出现形式为否定的变量,因为 V V V对第 q q q行所有变量的赋值为 0 0 0。 E E E是空子句,不含任何变量,所以在归结路径上子句中第 q q q行的变量个数从 n − 1 n-1 n−1开始到 0 0 0结束,中间有增有减,不过减的时候最多减 1 1 1。因此,总有一时刻使得第 q q q行的变量个数恰为 2 k 2k 2k,这个子句就代表 V V V的半零子句。∎
如果一个子句 D D D经历若干次归结后得到子句 C C C,则称 D D D是 C C C的一个前驱子句。
引理3 设 R R R中有子句 C C C在关键赋值 V V V下的取值为假,且 V V V的零行为第 q q q行。则要么 C C C中至少包含 2 k 2k 2k个以肯定的形式出现的第 q q q行的变量,要么 C C C的某个前驱子句 D D D是半零子句且代表 V V V。
证明提要:还是考虑第 q q q行的变量个数。如果 C C C中包含的第 q q q行的变量个数小于 2 k 2k 2k,因为归结的过程中第 q q q行的变量个数每次至多减 1 1 1,所以一定有某个前驱子句 D D D中第 q q q行的变量个数是 2 k 2k 2k。∎
四、相邻的关键赋值
设 V V V和 W W W是两个关键赋值,并设 q , r q,r q,r分别是 V V V和 W W W关键行的编号。如果 W W W是 V V V交换 q , r q,r q,r两行的结果,则称 W W W和 V V V是相邻的。我们说 W W W是 V V V的 r r r-邻居, V V V是 W W W的 q q q-邻居。
引理4 设半零子句 C C C代表关键赋值 V V V,其中 V V V的零行为第 q q q行。设 r r r是不同于第 q q q行的一行,并设列 s s s和行 r r r关于 V V V对应(即 V V V给 P r s P_{rs} Prs赋值为 1 1 1)。假设 P q s P_{qs} Pqs在 C C C中不以肯定的形式出现(可以不出现), P r s P_{rs} Prs在 C C C中不以否定的形式出现(可以不出现),则 V V V的 r r r-邻居 W W W使 C C C的取值为假。
证明: V V V的第 r r r行只给一个变量 P r s P_{rs} Prs赋值为 1 1 1,因此 V V V和 W W W只有对 P q s P_{qs} Pqs、 P r s P_{rs} Prs的赋值有区别。考虑变量 P q s P_{qs} Pqs,它在 C C C中不以肯定的形式出现,那它要么不出现、要么以否定的形式出现。但是如果它以否定的形式出现,那么由于 V V V给 P q s P_{qs} Pqs的赋值为 0 0 0(这是因为 q q q是零行), C C C就被满足了,所以 P q s P_{qs} Pqs只能在 C C C中不出现。同理, P r s P_{rs} Prs要么不出现、要么以肯定的形式出现,但 V V V给 P q s P_{qs} Pqs的赋值为 1 1 1,所以只能不出现。因此, P q s P_{qs} Pqs和 P r s P_{rs} Prs在 C C C中均不出现,而 V V V和 W W W赋值的差异仅仅在于这两个变量,所以把 V V V换成 W W W对 C C C没有影响,因此 W W W使 C C C的取值为假。∎
五、高复杂度子句
高复杂度子句(highly complex clause, HCC)组成的集合 H C C \mathcal{HCC} HCC是半零子句组成的集合 H Z C \mathcal{HZC} HZC的一个子集。其具体定义将会在下面给出。
回想一下: F S 1 \mathrm{FS}1 FS1是所有 k k k个变量的集合 S S S的集合,使得 S S S中没有两个变量在同一行或同一列。我们给 F S 1 \mathrm{FS}1 FS1中的每一个集合 S S S分配一个半零子句 C S C_S CS。首先,定义 S S S- C T A \mathcal{CT\!\!A} CTA为给 S S S中每个变量赋值为 1 1 1的关键赋值的集合。( F S 1 \mathrm{FS}1 FS1代表“fixed set of 1’s”,即 S S S限定了关键赋值中的 k k k个取值为 1 1 1的变量)。接下来,令 S S S- H Z C \mathcal{HZC} HZC是所有能够代表 S S S- C T A \mathcal{CT\!\!A} CTA中某一关键赋值的半零子句 C C C的集合。根据引理2,集合 S S S- H Z C \mathcal{HZC} HZC非空。令 C S C_S CS是 S S S- H Z C \mathcal{HZC} HZC中第一个在 R R R中出现的子句。可以这么理解:对于集合 S S S,找出所有使 S S S中变量赋值为 1 1 1的关键赋值,再找出所有能代表这其中某一关键赋值的半零子句,取其中在 R R R中最早出现的子句即为 C S C_S CS。注意, C S C_S CS的任何前驱子句都不可能出现在 S S S- H Z C \mathcal{HZC} HZC中。令 H C C = { C S ∣ S ∈ F S 1 } \mathcal{HCC}=\{C_S|S\in\mathrm{FS}1\} HCC={CS∣S∈FS1}。
引理5 每个高复杂度子句都有至少 k + 1 k+1 k+1行,其中每行包含一个以否定形式出现的变量或至少 2 k 2k 2k个以肯定形式出现的变量。
证明:
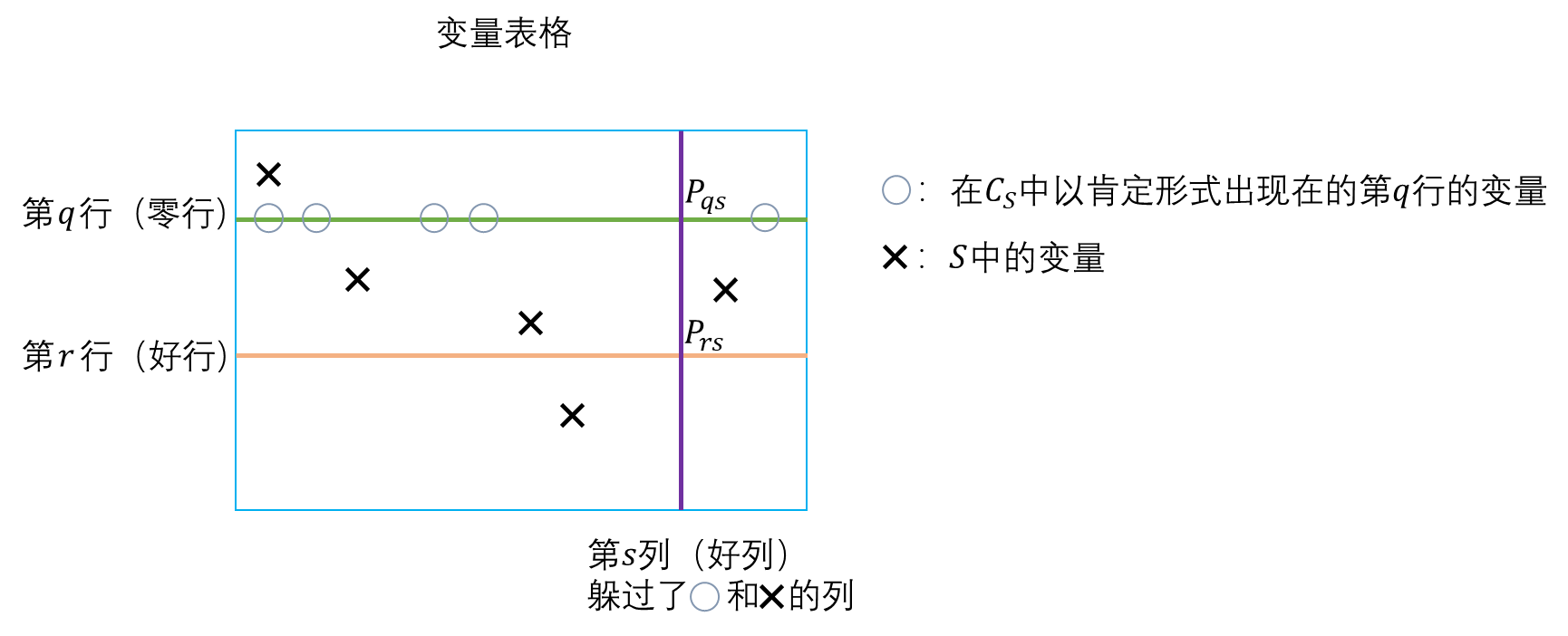
- 设 S ∈ F S 1 S\in\mathrm{FS}1 S∈FS1并设 C S C_S CS是对应的高复杂度子句。设 V V V是被 C S C_S CS代表的关键赋值,并设 V V V的零行是第 q q q行。由于 C S C_S CS是半零子句,变量表格第 q q q行有 2 k 2k 2k个变量在 C S C_S CS中以肯定的形式出现,并且表格的 k k k列有变量出现在 C S C_S CS中。抛开这些列,还剩 n − 1 − 3 k ≥ k n-1-3k\ge k n−1−3k≥k列(称为“好列”),好列的第 q q q行的变量不在 C S C_S CS中出现而且不包含在 S S S中出现的变量。每个好列关于 V V V对应于一个行,称为“好行”。(好行的定义)
- 设 r r r是一个好行,且令列 s s s和行 r r r关于 V V V相对应。要么有第 r r r行的某个变量在 C S C_S CS中以否定的形式出现,要么 C S C_S CS代表 V V V的 r r r-邻居 W W W(根据引理4,如果第 r r r行的所有变量都不以否定的形式在 C S C_S CS中出现,再结合好列 s s s第 q q q行的变量 P q s P_{qs} Pqs不在 C S C_S CS中出现,那么 C S C_S CS就代表 V V V的 r r r-邻居 W W W)。(好列的定义,引入 r r r-邻居 W W W)
- 现在处理 C S C_S CS代表 W W W的情况。
- 因为 V ∈ S V\in S V∈S- C T A \mathcal{CT\!\!A} CTA,所以 S S S中的每个变量必须在 V V V中的赋值为 1 1 1。因此,第 q q q行的变量都不出现在 S S S中。第 r r r行的变量也都不出现在 S S S中,因为第 r r r行和第 s s s列对应,第 r r r行如果有 S S S中的变量也一定是 P r s P_{rs} Prs,但第 s s s列是好列,所以不含 S S S中的变量。这也就意味着,在 V V V中交换 q q q、 r r r两行不改变 S S S中变量的赋值。所以, W ∈ S W\in S W∈S- C T A \mathcal{CT\!\!A} CTA。(证明 W ∈ S W\in S W∈S- C T A \mathcal{CT\!\!A} CTA)
- 由于 C S C_S CS是 S S S- H Z C \mathcal{HZC} HZC中第一个出现在 R R R中的子句,而所有代表 W W W的子句在 S S S- H Z C \mathcal{HZC} HZC中,因此 C S C_S CS的任何前驱子句都不能代表 W W W。 W W W的零行为第 r r r行, C S C_S CS代表 W W W,用 C S C_S CS和 W W W套用引理3(注意“要么-要么”的第二个要么不成立,所以只有第一个要么成立),得:第 r r r行必然有 2 k 2k 2k个变量以肯定的形式在 C S C_S CS中出现。(分析 C S C_S CS代表 W W W的情况下好行的性质)
- 回顾绿色句子,可知所有好行满足引理5中的条件。所以,第 q q q行和所有的好行构成了引理5中提到的 k + 1 k+1 k+1行。(得到引理5中提到的 k + 1 k+1 k+1行)
示意图:
六、函数 f ( n ) f(n) f(n)
回顾一下 h ( n ) = ∣ F S 1 ∣ h(n)=|\mathrm{FS}1| h(n)=∣FS1∣。 F S 1 \mathrm{FS}1 FS1中的每个元素都对应一个高复杂度子句,但这个映射不一定是单射。我们需要给出一个高复杂度子句对应的 F S 1 \mathrm{FS}1 FS1中的元素的个数上界,该上界即为 g ( n ) g(n) g(n)。
设 C ∈ H C C C\in\mathcal{HCC} C∈HCC。若 C C C是对应于 F S 1 \mathrm{FS}1 FS1中某个元素 S S S的 C S C_S CS,那么 S S S中的变量在 C C C中要么不出现,要么以否定的形式出现(注意 C S C_S CS代表了 S S S- C T A \mathcal{CT\!\!A} CTA中的某个关键赋值,而这个关键赋值对 S S S中元素的赋值为 1 1 1)。根据引理1, C S C_S CS每行至多只有一个以否定形式出现的变量。我们用 C C C的复杂性来限制在 F S 1 \mathrm{FS}1 FS1中选择 S S S使得 C = C S C=C_S C=CS的方案数。为了得到 g ( n ) g(n) g(n),我们数出给 P H P n n − 1 \mathrm{PHP}_{n}^{n-1} PHPnn−1的变量赋 k k k个 1 1 1的方案数,这些方案使得没有两个赋值为 1 1 1的变量在同一行或同一列, C C C中以肯定形式出现的变量赋值为 0 0 0,且如果某一行的一个变量在 C C C中以否定形式出现,则这个变量是这一行唯一可以赋值为 1 1 1的变量。每个这种赋 k k k个 1 1 1的方法对应 F S 1 \mathrm{FS}1 FS1中的一个 S S S。
设 A A A是引理5中提到的 C C C的 k + 1 k+1 k+1行,其中每行包含一个以否定形式出现的变量或至少 2 k 2k 2k个以肯定形式出现的变量。对于 A A A的每一行,我们至多可以给其中 n − 1 − 2 k n-1-2k n−1−2k个变量赋值为 1 1 1(如果该行有一个以否定形式出现的变量,则只能赋一个 1 1 1;如果有 2 k 2k 2k个以肯定形式出现的变量,则可以赋 n − 1 − 2 k n-1-2k n−1−2k个 1 1 1)。当我们赋 k k k个 1 1 1的时候,存在一个数 i i i使得其中 i i i个 1 1 1是在 A A A的 k + 1 k+1 k+1行中出现的,剩余 k − i k-i k−i个 1 1 1是在除 A A A之外的剩下 n − k − 1 n-k-1 n−k−1行中出现的。 i i i可以是 0 0 0到 i i i的任意值。给定一个 i i i,有 d i d_i di种方法选择含有 1 1 1的行,其中 d i = C k + 1 i C n − k − 1 k − i d_i=C_{k+1}^{i} C_{n-k-1}^{k-i} di=Ck+1iCn−k−1k−i。对于 A A A中的 i i i行,我们有至多 ( n − 1 − 2 k ) i {(n-1-2k)}^i (n−1−2k)i中方法选择 1 1 1出现在哪一列(这个界很松,虽然我们应该考虑列不能重复,但我们不知道能选的 n − 1 − 2 k n-1-2k n−1−2k列究竟是哪些列,所以也就无法避免重复的列了)。对于不在 A A A中的行,我们至多有 A n − 1 − i k − i = ( n − 1 − i ) ! ( n − 1 − k ) ! A_{n-1-i}^{k-i}=\cfrac{(n-1-i)!}{(n-1-k)!} An−1−ik−i=(n−1−k)!(n−1−i)!种选法来选择 1 1 1出现在哪一列,因为每一列只能用一次。所以, g ( n ) = ∑ i = 0 k d i ( n − 1 − 2 k ) i ( n − 1 − i ) ! ( n − 1 − k ) ! g(n)=\sum\limits_{i=0}^k d_i{(n-1-2k)}^i\cfrac{(n-1-i)!}{(n-1-k)!} g(n)=i=0∑kdi(n−1−2k)i(n−1−k)!(n−1−i)!对于 h ( n ) = ∣ F S 1 ∣ h(n)=|\mathrm{FS}1| h(n)=∣FS1∣,考虑选 k k k个行,共有 C n k C_n^k Cnk种选法;再从 n − 1 n-1 n−1列中选 k k k列,共有 A n − 1 k = ( n − 1 ) ! ( n − 1 − k ) ! A_{n-1}^k=\cfrac{(n-1)!}{(n-1-k)!} An−1k=(n−1−k)!(n−1)!种选法。所以 h ( n ) = C n k A n − 1 k = C n k ( n − 1 ) ! ( n − 1 − k ) ! h(n)=C_n^k A_{n-1}^k=C_n^k \cfrac{(n-1)!}{(n-1-k)!} h(n)=CnkAn−1k=Cnk(n−1−k)!(n−1)!利用组合数恒等式 C n k = ∑ i = 0 k C k + 1 i C n − k − 1 k − i = ∑ i = 0 k d i C_n^k=\sum\limits_{i=0}^{k} C_{k+1}^{i} C_{n-k-1}^{k-i}=\sum\limits_{i=0}^{k} d_i Cnk=i=0∑kCk+1iCn−k−1k−i=i=0∑kdi(可理解为:先在 k + 1 k+1 k+1个中选 i i i个,再在 n − k − 1 n-k-1 n−k−1个中选 k − i k-i k−i个),我们得到 h ( n ) = ∑ i = 0 k d i ( n − 1 ) ! ( n − 1 − i ) ! ( n − 1 − i ) ! ( n − 1 − k ) ! h(n)=\sum\limits_{i=0}^{k} d_i\cfrac{(n-1)!}{(n-1-i)!}\cfrac{(n-1-i)!}{(n-1-k)!} h(n)=i=0∑kdi(n−1−i)!(n−1)!(n−1−k)!(n−1−i)!所以 f ( n ) = h ( n ) g ( n ) = ∑ i = 0 k d i ∑ i = 0 k d i ( n − 1 − i ) ! ( n − 1 − 2 k ) i ( n − 1 ) ! f(n)=\cfrac{h(n)}{g(n)}=\cfrac{\sum\limits_{i=0}^{k} d_i}{\sum\limits_{i=0}^{k} d_i\cfrac{(n-1-i)!{(n-1-2k)}^i}{(n-1)!}} f(n)=g(n)h(n)=i=0∑kdi(n−1)!(n−1−i)!(n−1−2k)ii=0∑kdi令 n ≥ 201 n\ge 201 n≥201。考虑放大 ( n − 1 − i ) ! ( n − 1 − 2 k ) i ( n − 1 ) ! \cfrac{(n-1-i)!{(n-1-2k)}^i}{(n-1)!} (n−1)!(n−1−i)!(n−1−2k)i。当 i ≤ k i\le k i≤k时, n − 1 − 2 k n − 1 − i ≤ n − 1 − 2 k n − 1 − k ≤ 2 k + 1 3 k < 1 1.49 \cfrac{n-1-2k}{n-1-i}\le\cfrac{n-1-2k}{n-1-k}\le\cfrac{2k+1}{3k}<\cfrac{1}{1.49} n−1−in−1−2k≤n−1−kn−1−2k≤3k2k+1<1.491,故 ( n − 1 − 2 k ) i ≤ ( n − 1 − i ) i 1.49 i {(n-1-2k)}^i\le\cfrac{{(n-1-i)}^i}{{1.49}^i} (n−1−2k)i≤1.49i(n−1−i)i。因此 ( n − 1 − i ) ! ( n − 1 − 2 k ) i ( n − 1 ) ! ≤ ( n − 1 − i ) ! ( n − 1 ) i ( n − 1 ) ! 1.49 i = ( n − i ) ⋅ ( n − i ) ⋅ ⋯ ⋅ ( n − i ) ( n − 1 ) ⋅ ( n − 2 ) ⋅ ⋯ ⋅ ( n − i ) 1 1.49 i ≤ 1 ⋅ 1 1.49 i = 1 1.49 i \cfrac{(n-1-i)!{(n-1-2k)}^i}{(n-1)!}\le\cfrac{(n-1-i)!{(n-1)}^i}{(n-1)!{1.49}^i}=\cfrac{(n-i)\cdot(n-i)\cdot\cdots\cdot(n-i)}{(n-1)\cdot(n-2)\cdot\cdots\cdot(n-i)}\cfrac{1}{{1.49}^i}\le 1\cdot\cfrac{1}{{1.49}^i}=\cfrac{1}{{1.49}^i} (n−1)!(n−1−i)!(n−1−2k)i≤(n−1)!1.49i(n−1−i)!(n−1)i=(n−1)⋅(n−2)⋅⋯⋅(n−i)(n−i)⋅(n−i)⋅⋯⋅(n−i)1.49i1≤1⋅1.49i1=1.49i1。于是我们有 f ( n ) > ∑ i = 0 k d i ∑ i = 0 k d i 1.49 i ( ∗ ) f(n)>\cfrac{\sum\limits_{i=0}^{k} d_i}{\sum\limits_{i=0}^{k} \cfrac{d_i}{{1.49}^i}}\qquad(*) f(n)>i=0∑k1.49idii=0∑kdi(∗)令 m = ⌊ n − 1 50 ⌋ m=\left\lfloor\cfrac{n-1}{50}\right\rfloor m=⌊50n−1⌋。当 i + 1 ≤ 2 m i+1\le 2m i+1≤2m时, d i + 1 d i = ( k + 1 − i ) ( k − i ) ( i + 1 ) ( n − 2 k + i ) > [ ( n − 1 ) / 5 ] [ ( n − 1 ) / 5 ] [ ( n − 1 ) / 25 ] [ 0.6 ( n − 1 ) ] > 1.5 \cfrac{d_{i+1}}{d_i}=\cfrac{(k+1-i)(k-i)}{(i+1)(n-2k+i)}>\cfrac{[(n-1)/5][(n-1)/5]}{[(n-1)/25][0.6(n-1)]}>1.5 didi+1=(i+1)(n−2k+i)(k+1−i)(k−i)>[(n−1)/25][0.6(n−1)][(n−1)/5][(n−1)/5]>1.5故 ∑ i = 0 m − 1 d i 1.49 i ≤ ∑ i = m 2 m − 1 d i 1.49 i ( † ) \sum\limits_{i=0}^{m-1}\cfrac{d_i}{{1.49}^i}\le\sum\limits_{i=m}^{2m-1}\cfrac{d_i}{{1.49}^i}\qquad(\dagger) i=0∑m−11.49idi≤i=m∑2m−11.49idi(†)考虑 ( ∗ ) (*) (∗)式不等号右端的分式,记分子为 Φ \Phi Φ,分母为 Ψ \Psi Ψ。对分母 Ψ \Psi Ψ应用 ( † ) (\dagger) (†)式并放大得 Ψ = ∑ i = 0 k d i 1.49 i ≤ ( 2 ∑ i = m 2 m − 1 + ∑ i = 2 m k ) d i 1.49 i < 2 ∑ i = m k d i 1.49 i < 2 ∑ i = m k d i 1.49 m \Psi=\sum\limits_{i=0}^{k} \cfrac{d_i}{{1.49}^i}\le\left(2\sum\limits_{i=m}^{2m-1}+\sum\limits_{i=2m}^{k}\right)\cfrac{d_i}{{1.49}^i}<2\sum\limits_{i=m}^{k}\cfrac{d_i}{{1.49}^i}<2\sum\limits_{i=m}^{k}\cfrac{d_i}{{1.49}^m} Ψ=i=0∑k1.49idi≤(2i=m∑2m−1+i=2m∑k)1.49idi<2i=m∑k1.49idi<2i=m∑k1.49mdi对分母缩小得 Φ = ∑ i = 0 k d i > ∑ i = m k d i \Phi=\sum\limits_{i=0}^{k} d_i>\sum\limits_{i=m}^{k} d_i Φ=i=0∑kdi>i=m∑kdi于是 f ( n ) > ∑ i = m k d i 2 ∑ i = m k d i 1.49 m = 1.49 m 2 > ( 1.49 0.01 ) n f(n)>\cfrac{\sum\limits_{i=m}^k d_i}{2\sum\limits_{i=m}^k\cfrac{d_i}{{1.49}^m}}=\cfrac{{1.49}^m}{2}>{({1.49}^{0.01})}^n f(n)>2i=m∑k1.49mdii=m∑kdi=21.49m>(1.490.01)n所以,对于任意 n ≥ 201 n\ge 201 n≥201, f ( n ) > c n f(n)>c^n f(n)>cn,其中 c = 1.49 0.01 c={1.49}^{0.01} c=1.490.01。
Q.E.D. \text{Q.E.D.} Q.E.D.
值得注意的是,虽然命题鸽巢原理有指数级归结下界,但它有多项式大小的弗雷格证明(Buss 1987[2])和扩展弗雷格证明(Cook 1976[3])。它的指数级归结下界不能说明它太难,只能说明归结证明系统太弱。
参考文献
[1] Haken, Armin. “The Intractability of Resolution.” Theor. Comput. Sci. 39 (1985): 297-308.
[2] Buss, Samuel R. “Polynomial size proofs of the propositional pigeonhole principle.” Journal of Symbolic Logic 52 (1987): 916 - 927.
[3] Cook, Stephen A. “A short proof of the pigeon hole principle using extended resolution.” SIGACT News 8 (1976): 28-32.
相关文章:

【计算复杂性理论】证明复杂性(八):命题鸽巢原理(Propositional Pigeonhole Principle)的指数级归结下界
往期文章: 【计算复杂性理论】证明复杂性(Proof Complexity)(一):简介 【计算复杂性理论】证明复杂性(二):归结(Resolution)与扩展归结ÿ…...
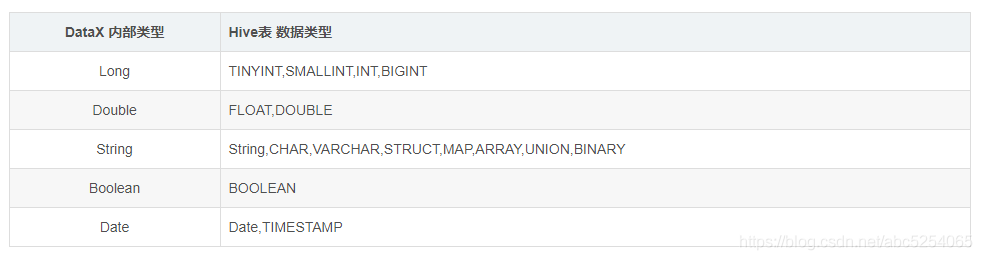
使用DataX实现mysql与hive数据互相导入导出
一、概论 1.1 什么是DataX DataX 是阿里巴巴开源的一个异构数据源离线同步工具,致力于实现包括关系型数据库(MySQL、Oracle 等)、HDFS、Hive、ODPS、HBase、FTP 等各种异构数据源之间稳定高效的数据同步功能。 1.2 DataX 的设计 为了解决异构数据源同步问题…...
语音转录成文本:AI Transcription for mac
AI Transcription是一种人工智能技术,它可以将音频和视频文件转换成文本格式。这种技术可以帮助用户快速地将大量的音频和视频内容转换成文本格式,方便用户进行文本分析、搜索和编辑等操作。 以下是AI Transcription的几个特点: 高效性。AI …...
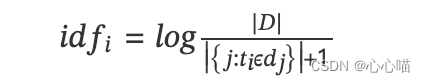
[nlp] TF-IDF算法介绍
(1)TF是词频(Term Frequency) 词频是文档中词出现的概率。 (2) IDF是逆向文件频率(Inverse Document Frequency) 包含词条的文档越少,IDF越大。...

一些感想,写在8月之前
最近换工作了,离开了一个奋斗了4年多的公司,现在在新公司,还在培训中,不那么忙了,就写写最近的想法吧。 因为最近一直在研究框架和搭项目框架,所以就想把一些工作上的过程记录下来,以备不时之需…...

推动数字经济高质量发展需破解三大挑战
随着信息技术的飞速发展,数字经济已成为全球经济发展的重要驱动力。数字经济以其高效、便捷、创新的特点,深刻改变着传统产业和商业模式,为经济发展带来新的活力和动力。然而,要实现数字经济的高质量发展,仍然面临着三…...
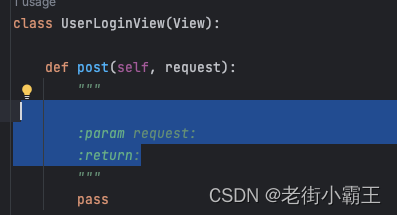
Pycharm工具Python开发自动添加注释(详细)
方法自动添加参数注释 定义了一个函数,在函数下面敲入了三个双引号后,enter回车并没有自动出现注释,如图: 解决办法 Pycharm中依次打开File —> Settings —> Tools —> Python Integrated Tools,如图&…...

RUST 有哪些整型?
在Rust中,有以下几种整型数据类型: i8 :有符号8位整型,取值范围为-128到127。u8 :无符号8位整型,取值范围为0到255。i16 :有符号16位整型,取值范围为-32768到32767。u16 ࿱…...
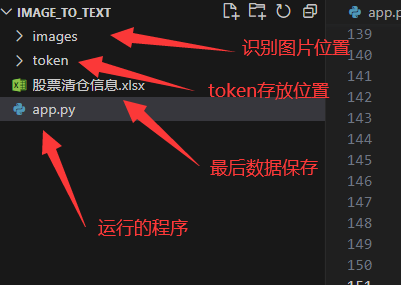
【Python 实战】---- 批量识别图片中的文字,存入excel中【使用百度的通用文字识别】
分析 1. 获取信息图片示例 2. 运行实例 3. 运行结果 4. 各个文件的位置 实现 1. 需求分析 识别图片中的文字【采用百度的通用文字识别】;文字筛选,按照分类获取对应的文本;采用 openpyxl 实现将数据存入 excel 中。2. 获取 access_token 获取本地缓存的...

探索前端图片如何携带token进行验证
前言 图片在前端开发中扮演了重要的角色,它们不仅仅是美观的元素,还可以传递信息和激发用户的兴趣。随着应用场景的增多,前端开发人员就需要在图片加载过程中携带验证的信息。如 token,用于身份验证、权限控制等方面。通过在图片的…...

飞桨AI Studio可以玩多模态了?MiniGPT4实战演练!
MiniGPT4是基于GPT3的改进版本,它的参数量比GPT3少了一个数量级,但是在多项自然语言处理任务上的表现却不逊于GPT3。项目作者以MiniGPT4-7B作为实战演练项目。 创作者:衍哲 体验链接: https://aistudio.baidu.com/aistudio/proj…...

C++笔记之++i和i++是原子操作吗?
C笔记之i和i是原子操作吗? code review! 文章目录 C笔记之i和i是原子操作吗?1.i是原子操作吗?2.i是原子操作吗?3.前置递增和后置递增 1.i是原子操作吗? 2.i是原子操作吗? 3.前置递增和后置递增...
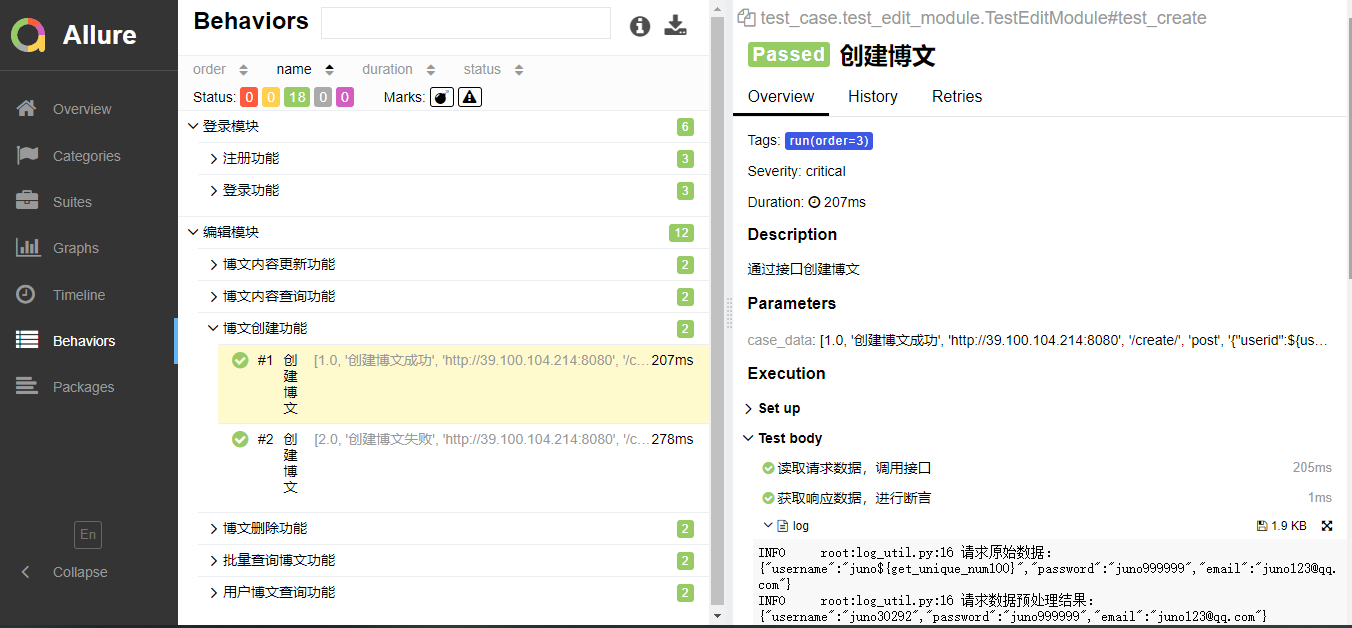
Pytest+Allure+Excel接口自动化测试框架实战
1. Allure 简介 简介 Allure 框架是一个灵活的、轻量级的、支持多语言的测试报告工具,它不仅以 Web 的方式展示了简介的测试结果,而且允许参与开发过程的每个人可以从日常执行的测试中,最大限度地提取有用信息。 Allure 是由 Java 语言开发…...

阿里云国际版账号注册常见问题汇总
公司现与阿里云国际站达成战略合作,为客户提供高品质、高性能、高可用的阿里云产品与服务,助力客户用云服务创造更多价值,达成业务转型、加速和创新,全面提升业务竞争力。助企业在各种业务场景中充分利用混合云基础设施进行优化。…...

Flowable基础
简介 Flowable 是 BPMN 的一个基于 java 的软件实现,不过 Flowable 不仅仅包括 BPMN ,还有 DMN 决策表和 CMMN Case 管理引擎,并且有自己的用户管理、微服务 API 等一系列功能, 是一个服务平台。 官方手册: https://…...
力扣热门100题之合并区间【中等】
题目描述 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 1: 输入:interv…...

机会成本:隐形的手,驱动你的选择
机会成本这个词不知道你有没有听说过。 机会成本是指在面临多方案择一决策时,被舍弃的选项中的最高价值者。换句话说,机会成本是一种失去的收益,不是实际支付的成本。 机会成本是经济学中一个非常重要的概念,它可以帮助我们更好地…...

win10日程怎么同步到安卓手机?电脑日程同步到手机方法
在如今快节奏的生活中,高效地管理时间变得至关重要。而对于那些经常在电脑上安排日程的人来说,将这些重要的事务同步到手机上成为了一个迫切的需求。因为目前国内使用win10系统电脑、安卓手机的用户较多,所以越来越多的职场人士想要知道&…...

7月31日每日两题
第一题:再解炸弹人 小哼最近爱上了“炸弹人”游戏。你还记得在小霸王游戏机上的炸弹人吗?用放置炸弹的方法来消灭敌人。需将画面上的敌人全部消灭后,并找到隐藏在墙里的暗门才能过关。 现在有一个特殊的关卡如下。你只有一枚炸弹,但是这枚炸弹威力超强(杀伤距离超长,可…...

首期华为云ROMA Connect《企业集成战略与华为数字化之道》高研班在东莞圆满举办
7月25日,首期华为云ROMA Connect《企业集成战略与华为数字化之道》高研班在东莞华为制造业数字化转型中心圆满举办。 20多家东莞精密机械、电子、环保等领域的先进企业董事长、总经理、CIO、总监等高管参加培训。 本次高研班邀请到华为数字化转型专家陈劲、马兵东…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
