JavaScript---事件对象event
获取事件对象：
事件对象：是个对象，这个对象里有事件触发时的相关信息，在事件绑定的回调函数的第一个参数就是事件对象，一般命名为event、ev、e
eg: 元素.addEventListener('click',function (e){})
部分常用属性：
type: 获取当前事件类型
clientX / clientY: 获取光标相对于浏event览器可见窗口左上角位置
offsetX / offsetY: 获取光标相对于当前dom元素左上角位置
key: 用户按下的键盘的值 现在不提倡使用keyCode
<body>
<input type="text">
<script>const input = document.querySelector("input")input.addEventListener("keyup",function (e){console.log(e.key)if (e.key==='Enter'){console.log("我按下了回车键")}})
</script>
</body>相关文章：
JavaScript---事件对象event
获取事件对象： 事件对象：是个对象，这个对象里有事件触发时的相关信息，在事件绑定的回调函数的第一个参数就是事件对象，一般命名为event、ev、e eg: 元素.addEventListener(click,function (e){}) 部分常用属性&…...
Day 15 C++对象模型和this指针
目录 C对象模型 类内的成员变量和成员函数分开存储 总结 this指针 概念 示例 用途 当形参和成员变量同名时 在非静态成员函数中，如果希望返回对象本身 例子 空指针访问成员函数 示例 const修饰成员函数 常函数（const member function&…...
HarmonyOS/OpenHarmony元服务开发-卡片生命周期管理
创建ArkTS卡片，需实现FormExtensionAbility生命周期接口。 1.在EntryFormAbility.ts中，导入相关模块。 import formInfo from ohos.app.form.formInfo; import formBindingData from ohos.app.form.formBindingData; import FormExtensionAbility from …...
软件工程01
软件工程原则： 开闭原则： open closed principle ： 对扩展开放，对修改关闭，，，只让扩展，不让修改，用新增的类去替代修改的类 扩展之后，代码不用改变ÿ…...
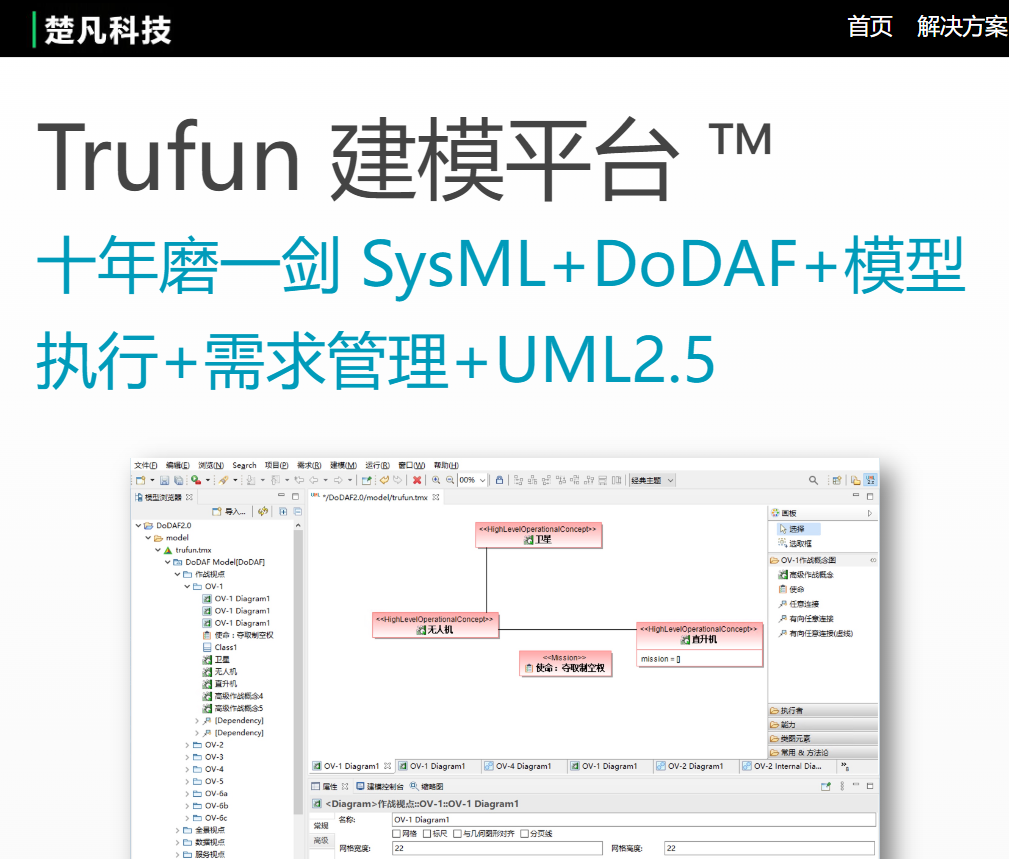
UML/SysML建模工具更新（2023.7）（1-5）有国产工具
DDD领域驱动设计批评文集 欢迎加入“软件方法建模师”群 《软件方法》各章合集 最近一段时间更新的工具有： 工具最新版本：Visual Paradigm 17.1 更新时间：2023年7月11日 工具简介 很用心的建模工具。支持编写用例规约。支持文本分析和C…...
Mac plist文件
macOS、iOS、iPadOS的应用程序都可能会有plist配置文件，他是苹果系列操作系统特有的配置文件。 plist的本质是个xml格式的文本文件，英文全称是property list，文件后缀使用.plist。 对于普通用户来说，基本不用管plist文件是什么&…...
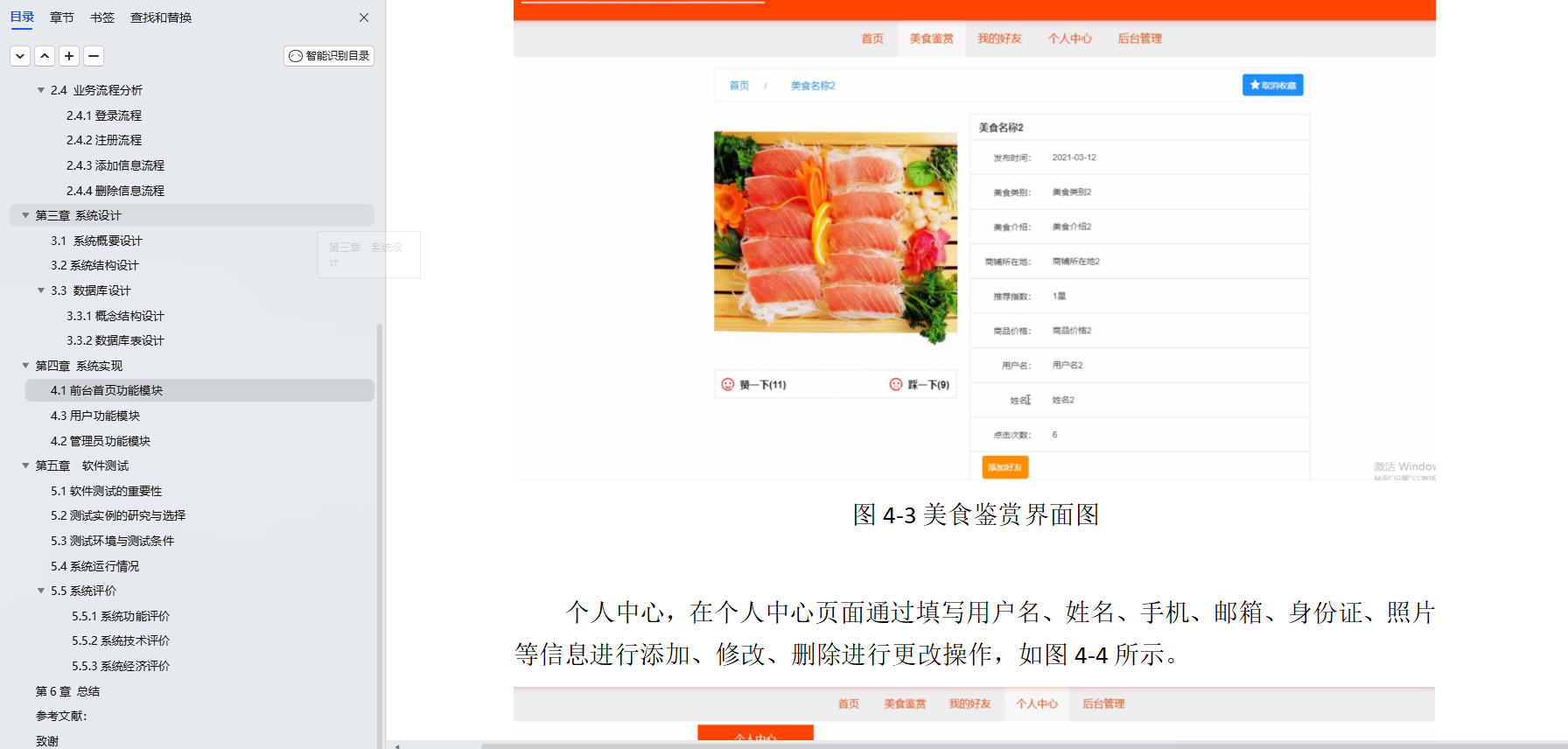
基于Java+SpringBoot+vue前后端分离校园周边美食探索分享平台设计实现
博主介绍：✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...
【openwrt】package介绍
openwrt package介绍 OpenWrt 构建系统主要围绕package的概念展开。不管是什么软件，几乎都对应一个package。 这几乎适用于系统中的所有内容：HOST工具、交叉编译工具链、Linux 内核、内核mod、根文件系统和上层的应用软件。 一个 OpenWrt package本质上…...
vue 封装一个鼠标拖动选择时间段功能
<template><div class"timeRange"><div class"calendar"><table><thead><tr><th rowspan"6" class"weekRow"><b>周/时间</b></th><th colspan"24"><…...
ubuntu22.0安装Barrier局域网共享鼠标键盘
ubuntu22.0安装Barrier局域网共享鼠标键盘 参考网站安装步骤客户端一直开启中解决 参考网站 https://idroot.us/install-barrier-ubuntu-22-04/ 安装步骤 sudo apt update sudo apt upgrade sudo apt install wget apt-transport-https gnupg2 software-properties-common s…...
ffmpeg常用功能博客导航
FFmpeg 是一个处理视频和音频内容的开源工具库，可以实现编码、解码、转码、流媒体和后处理等服务。 推荐博客： 常见命令和使用案例 用ffmpeg转mov为mp4格式 FFmpeg 常用命令 FFmpeg 常用命令编辑音/视频（转换格式、压缩、裁剪、截图、切分合…...
shopee，lazada，etsy店群如何高效安全的管理
对于电商卖家来说，要经营多个店铺，管理多个账号是非常常见的操作。为了避免账号关联被平台识别出来，需要使用防关联的浏览器来进行操作 1、支持多平台 支持同时管理多个电商平台店铺，Shopee、Lazada、etsy、poshmark、vinted等&…...
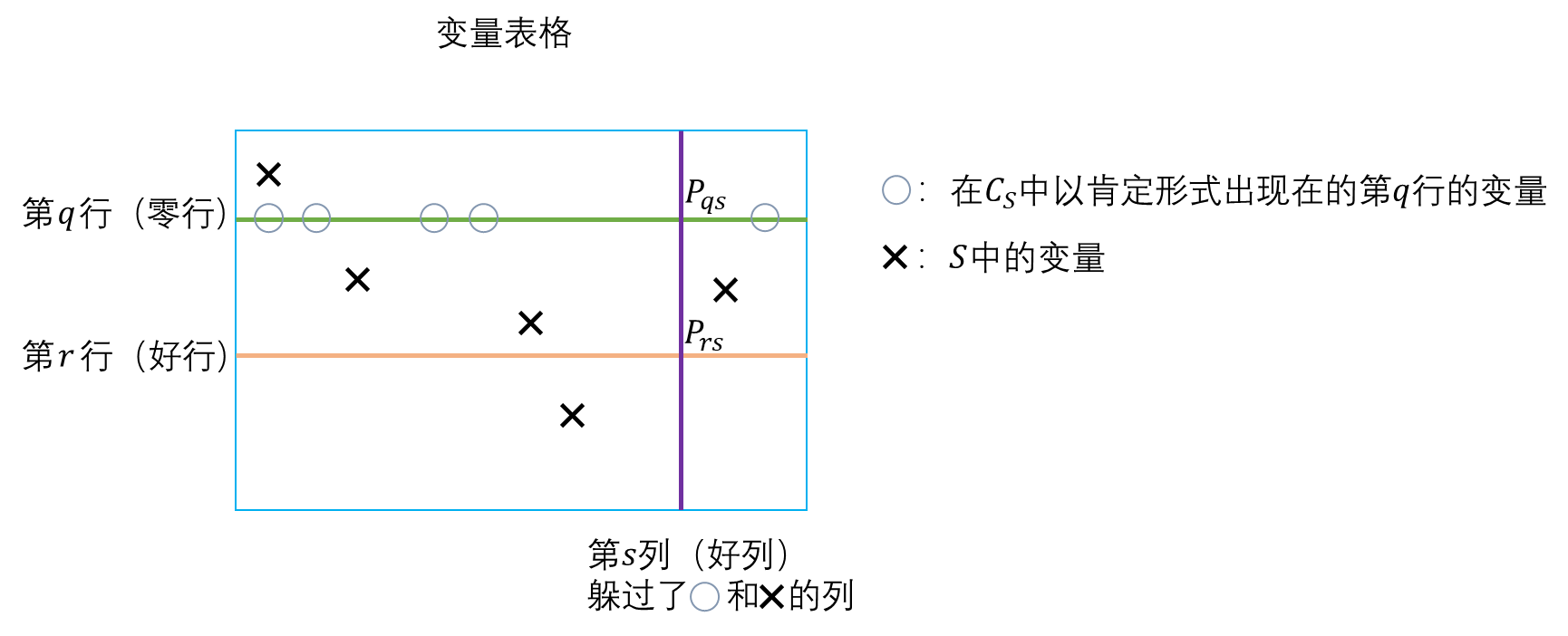
【计算复杂性理论】证明复杂性（八）：命题鸽巢原理（Propositional Pigeonhole Principle）的指数级归结下界
往期文章： 【计算复杂性理论】证明复杂性（Proof Complexity）（一）：简介 【计算复杂性理论】证明复杂性（二）：归结（Resolution）与扩展归结ÿ…...
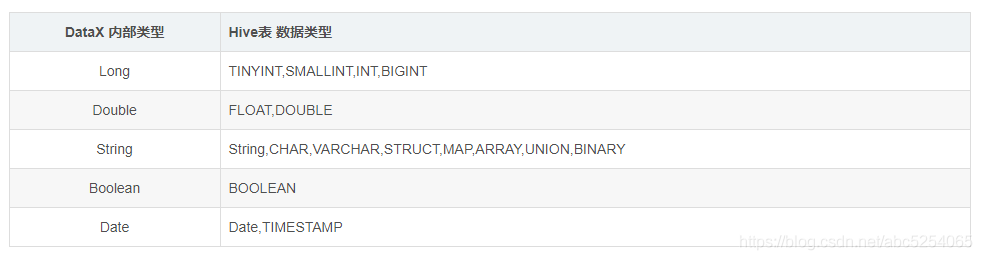
使用DataX实现mysql与hive数据互相导入导出
一、概论 1.1 什么是DataX DataX 是阿里巴巴开源的一个异构数据源离线同步工具，致力于实现包括关系型数据库(MySQL、Oracle 等)、HDFS、Hive、ODPS、HBase、FTP 等各种异构数据源之间稳定高效的数据同步功能。 1.2 DataX 的设计 为了解决异构数据源同步问题…...
语音转录成文本：AI Transcription for mac
AI Transcription是一种人工智能技术，它可以将音频和视频文件转换成文本格式。这种技术可以帮助用户快速地将大量的音频和视频内容转换成文本格式，方便用户进行文本分析、搜索和编辑等操作。 以下是AI Transcription的几个特点： 高效性。AI …...
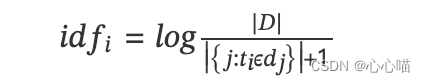
[nlp] TF-IDF算法介绍
（1）TF是词频(Term Frequency) 词频是文档中词出现的概率。 （2） IDF是逆向文件频率(Inverse Document Frequency) 包含词条的文档越少，IDF越大。...
一些感想，写在8月之前
最近换工作了，离开了一个奋斗了4年多的公司，现在在新公司，还在培训中，不那么忙了，就写写最近的想法吧。 因为最近一直在研究框架和搭项目框架，所以就想把一些工作上的过程记录下来，以备不时之需…...
推动数字经济高质量发展需破解三大挑战
随着信息技术的飞速发展，数字经济已成为全球经济发展的重要驱动力。数字经济以其高效、便捷、创新的特点，深刻改变着传统产业和商业模式，为经济发展带来新的活力和动力。然而，要实现数字经济的高质量发展，仍然面临着三…...
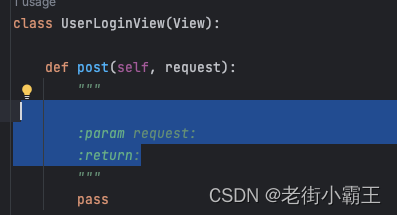
Pycharm工具Python开发自动添加注释（详细）
方法自动添加参数注释 定义了一个函数，在函数下面敲入了三个双引号后，enter回车并没有自动出现注释，如图： 解决办法 Pycharm中依次打开File —> Settings —> Tools —> Python Integrated Tools，如图&…...
RUST 有哪些整型？
在Rust中，有以下几种整型数据类型： i8 ：有符号8位整型，取值范围为-128到127。u8 ：无符号8位整型，取值范围为0到255。i16 ：有符号16位整型，取值范围为-32768到32767。u16 ࿱…...
RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数，对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
css实现圆环展示百分比，根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能，包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹，并新增内容 3.创建package文件夹...
相机Camera日志分析之三十一：高通Camx HAL十种流程基础分析关键字汇总（后续持续更新中）
【关注我，后续持续新增专题博文，谢谢！！！】 上一篇我们讲了：有对最普通的场景进行各个日志注释讲解，但相机场景太多，日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志，通过下列分类关键字搜索，即可清晰的分析不同场景的相机运行流程差异…...
Spring是如何解决Bean的循环依赖：三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中，Bean 的循环依赖是指多个 Bean 之间互相持有对方引用，形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路，例如： 双向依赖：Bean A 依赖 Bean B，同时 Bean B 也依赖 Bean A（A↔B）。链条循环： Bean A → Bean…...
【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统：Ubuntu 24.04 LTS (WSL2)架构：x86_64 (GNU/Linux)Rust 版本：rustc 1.87.0 (2025-05-09)Cargo 版本：cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
多模态图像修复系统：基于深度学习的图片修复实现
多模态图像修复系统：基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型（Stable Diffusion Inpainting）实现图像修复功能，结合文本描述和图片输入，对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
人工智能--安全大模型训练计划：基于Fine-tuning + LLM Agent
安全大模型训练计划：基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标：为安全大模型创建高质量、去偏、符合伦理的训练数据集，涵盖安全相关任务（如有害内容检测、隐私保护、道德推理等）。 1.1 数据收集 描…...
热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日，在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上，可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞，强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...