数学建模学习(8):单目标和多目标规划
优化问题描述

优化
优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值

线性规划
线性规划是指目标函数和约束都是线性的情况
[x,fval]=linprog(f,A,b,Aeq,Beq,LB,UB)
x:求得最优情况下变量的解
fval:求得最优目标值
f:目标函数的系数(符号按最小值标准,若目标是求解机大值可以通过添加负号改成求极小值)
A:不等式约束的变量系数(符合按小于标准,如果是大于约束可通过加负号变成小于)
b:不等式约束的常量
Aeq:等式约束的变量系数Beq:等式约束的常量LB:变量的下限UB:变量的上限

%% 线性规划
clc;clear;close all;
%目标函数/max 要改成min 的形式,max最大值可以系数加个负号的变成求min
f=[-1;-2;3]; %不等约束 /化成标准形式 x1+x2<=
% -x1-x2+0*x3<=-3
%0*x1-x2-x3<=-3
A=[-1,-1,0;0,-1,-1];%左边特征矩阵
b=[-3;-3]; %右边%等式约束
Aeq=[1,0,1];
Beq=[4];%变量约束,上限,下限
LB=zeros(3,1);
UB=2*ones(3,1);%优化
[x,fval]=linprog(f,A,b,Aeq,Beq,LB,UB);
%
objstr=['目标函数最优值:',num2str(fval)];
disp(objstr)
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
end非线性规划
非线性规划是指目标函数和约束有非线性的情况

%% 非线性规划1
clc;clear;close all;
%初始解,随意给个初始解
x0=zeros(3,1);%不等约束
A=[2,1,3];%左边特征矩阵
b=[6]; %右边%描述线性
%等式约束
Aeq=[];
Beq=[];%变量约束,上限,下限
LB=zeros(3,1);
UB=1*ones(3,1);%
%优化求解 max 加负号
fun = @(x)-x(1)^2+x(2)^2-x(2)*x(3);
%
nonlcon = @unitdisk;
[x,fval]=fmincon(fun,x0,A,b,Aeq,Beq,LB,UB,nonlcon);objstr=['目标函数最优值:',num2str(-fval)];%num2str 数字变成字符
disp(objstr)
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
endfunction [c,ceq] = unitdisk(x)
%c为不等式非线性约束
%ceq为等式非线性约束
c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;
%多个非线性约束的话,可以用[约束1;约束2];
ceq = [];
end%%
%遇到较为复杂的目标函数
%可以写为函数的形式
fun = @obj;
function y = obj(x)y1 = x(1)^2+x(2)^2;y = sqrt(y1)+x(3)^3;
end
%%多目标优化

多目标求解的第一种方法:
%% 非线性规划1
clc;clear;close all;
%%
%初始解,随意给个初始解
x0=zeros(3,1);%不等约束
A=[2,1,3];%左边特征矩阵
b=[6]; %右边%等式约束
Aeq=[];
Beq=[];%变量约束,上限,下限
LB=zeros(3,1);
UB=1*ones(3,1);
%优化求解
%%
w1=0.5;w2=0.5;
fun = @(x)(-x(1)^2+x(2)^2-x(2)*x(3))*w1+(2*x(1)^2-x(2)^3+2*x(2)*x(3))*w2;nonlcon = @unitdisk;
[x1,fval1]=fmincon(fun,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval1)];
disp(objstr)
for i=1:length(x1)xstr=['x',num2str(i),'的值为:',num2str(x1(i))];disp(xstr)
endfunction [c,ceq] = unitdisk(x)
%c为不等式非线性约束
%ceq为等式非线性约束
c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;
ceq = [];
end
多目标求解的第二种方法
%% 非线性规划1
clc;clear;close all;
%%
%初始解,随意给个初始解
x0=zeros(3,1);%不等约束
A=[2,1,3];%左边特征矩阵
b=[6]; %右边%等式约束
Aeq=[];
Beq=[];%变量约束,上限,下限
LB=zeros(3,1);
UB=1*ones(3,1);
%优化求解
%%
fun1 = @(x)-x(1)^2+x(2)^2-x(2)*x(3);
fun2 = @(x)2*x(1)^2-x(2)^3+2*x(2)*x(3);
%%
nonlcon = @unitdisk;
[x1,fval1]=fmincon(fun1,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval1)];
disp(objstr)
for i=1:length(x1)xstr=['x',num2str(i),'的值为:',num2str(x1(i))];disp(xstr)
end
[x2,fval2]=fmincon(fun2,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval2)];
disp(objstr)
for i=1:length(x2)xstr=['x',num2str(i),'的值为:',num2str(x2(i))];disp(xstr)
end
%% 多目标规划
goal=[fval1,fval2];
func = @(x)[-x(1)^2+x(2)^2-x(2)*x(3);2*x(1)^2-x(2)^3+2*x(2)*x(3)];
weight=[1,1];
[x,fival]=fgoalattain(func,x0,goal,weight,A,b,Aeq,Beq,LB,UB,nonlcon);
disp('在两个目标的优化结果为')
disp(func(x))
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
end
%%
function [c,ceq] = unitdisk(x)
%c为不等式非线性约束
%ceq为等式非线性约束
c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;
ceq = [];
end
%% 非线性规划1
clc;clear;close all;
%%
%初始解,随意给个初始解
x0=zeros(10,1);%不等约束
A=[];%左边特征矩阵
b=[]; %右边%等式约束
Aeq=[];
Beq=[];%变量约束,上限,下限
LB=-1*ones(10,1);LB(1)=0;
UB=1*ones(10,1);
%优化求解
%%
fun1 = @obj1;
fun2 = @obj2;
%%
nonlcon = [];
[x1,fval1]=fmincon(fun1,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval1)];
disp(objstr)
for i=1:length(x1)xstr=['x',num2str(i),'的值为:',num2str(x1(i))];disp(xstr)
end
[x2,fval2]=fmincon(fun2,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval2)];
disp(objstr)
for i=1:length(x2)xstr=['x',num2str(i),'的值为:',num2str(x2(i))];disp(xstr)
end
%% 多目标规划
goal=[fval1,fval2];
func = @obj3;
weight=[1,1];
[x,fival]=fgoalattain(func,x0,goal,weight,A,b,Aeq,Beq,LB,UB,nonlcon);
disp('在两个目标的优化结果为')
disp(func(x))
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
end
%%
function y1=obj1(x)[dim, num] = size(x);tmp = zeros(dim,num);tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;tmp1 = sum(tmp(3:2:dim,:)); % odd indextmp2 = sum(tmp(2:2:dim,:)); % even indexy1 = x(1,:) + 2.0*tmp1/size(3:2:dim,2);
% y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
end
function y2=obj2(x)[dim, num] = size(x);tmp = zeros(dim,num);tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;tmp1 = sum(tmp(3:2:dim,:)); % odd indextmp2 = sum(tmp(2:2:dim,:)); % even index
% y2 = x(1,:) + 2.0*tmp1/size(3:2:dim,2);y2 = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
end
function y=obj3(x)[dim, num] = size(x);tmp = zeros(dim,num);tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;tmp1 = sum(tmp(3:2:dim,:)); % odd indextmp2 = sum(tmp(2:2:dim,:)); % even indexy(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2);y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
end
% function [c,ceq] = unitdisk(x)
% %c为不等式非线性约束
% %ceq为等式非线性约束
% c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;
% ceq = [];
% end
相关文章:

数学建模学习(8):单目标和多目标规划
优化问题描述 优化 优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值 线性规划 线性规划是指目标函数和约束都是线性的情况 [x,fval]linprog(f,A,b,Aeq,Beq,LB,U…...

【Vscode | R | Win】R Markdown转html记录-Win
Rmd文件转html R语言环境Vscode扩展安装及配置配置radian R依赖包pandoc安装配置pandoc环境变量验证是否有效转rmd为html 注意本文代码块均为R语言代码,在R语言环境下执行即可 R语言环境 官网中去下载R语言安装包以及R-tool 可自行搜寻教程 无需下载Rstudio Vscod…...

【Lua语法】字符串操作、字符串中的方法
1.对字符串的操作 --声明一个字符串 str "我是一个字符串"--1.获取字符串的长度 -- 前面加个#即可(注意:Lua中字母占1个长度,汉字占3个长度) print(#str)--2.字符串多行打印 -- 方法1.Lua中是支持转义字符的 print("哈哈\n嘻嘻&q…...

Linux 终端生成二维码
1、安装qrencode [rootnode1 script]# yum -y install qrencode2、输出正常的 [rootnode1 ~]# echo https://www.github.com|qrencode -o - -t utf83、输出彩色的 [rootnode1 ~]# qrencode -t utf8 -s 1 https://www.github.com|lolcatPS:没有lolcat命令 #由于…...
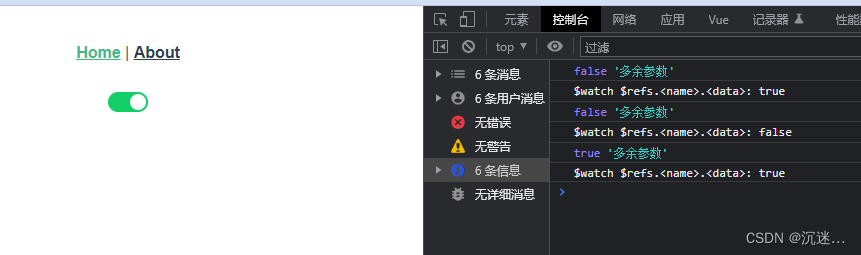
子组件未抛出事件 父组件如何通过$refs监听子组件中数据的变化
我们平时开发项目会使用一些比较成熟的组件库, 但是在极小的情况下,可能会出现我们需要监听某个属性的变化,使我们的页面根据这个属性发生一些改变,但是偏偏组件库没有把这个属性抛出来,当我们使用watch通过refs监听时,由于生命周期的原因还不能拿到,这时候我们可以这样做,以下…...
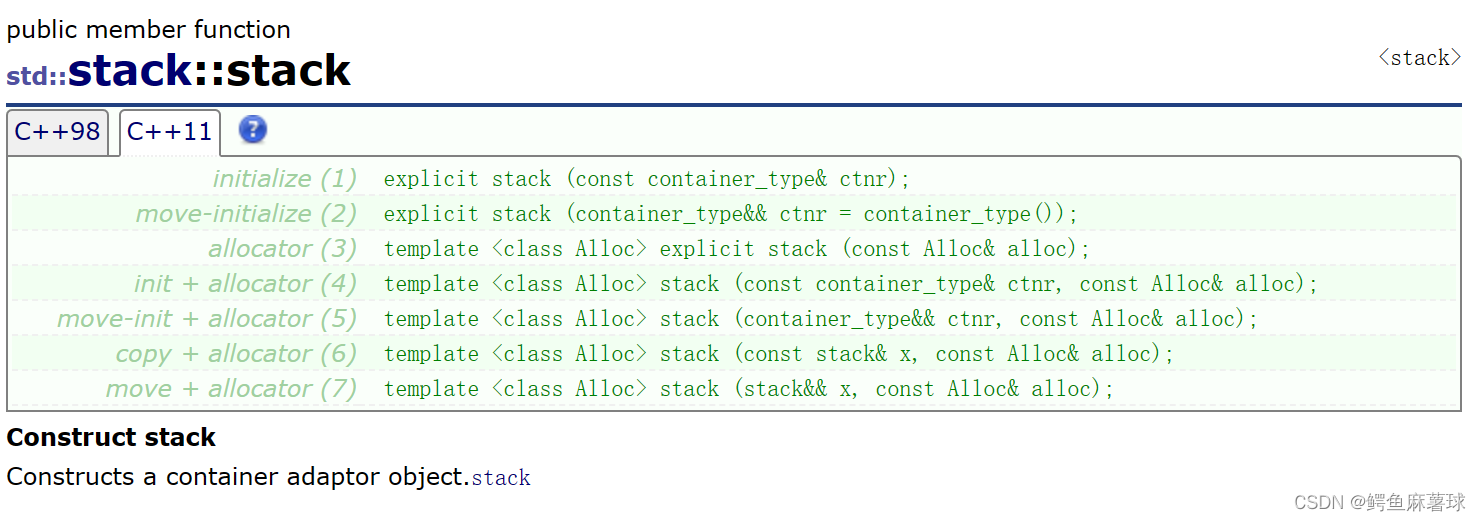
【C++】STL——stack的介绍和使用、stack的push和pop函数介绍和使用、stack的其他成员函数
文章目录 1.stack的介绍2.stack的使用2.1stack构造函数2.1stack成员函数(1)empty() 检测stack是否为空(2)size() 返回stack中元素的个数(3)top() 返回栈顶元素的引用(4)push() 将元素…...
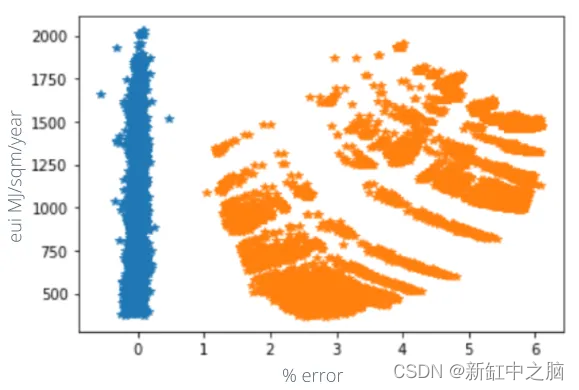
基于BIM+AI的建筑能源优化模型【神经网络】
推荐:用 NSDT设计器 快速搭建可编程3D场景。 AEC(建筑、工程、施工)行业的BIM 技术,允许在实际施工开始之前虚拟地建造建筑物; 这带来了许多有形和无形的好处:减少成本超支、更有效的协调、增强决策权等等。…...

#P0998. [NOIP2007普及组] 守望者的逃离
题目背景 恶魔猎手尤迪安野心勃勃,他背叛了暗夜精灵,率领深藏在海底的娜迦族企图叛变。 题目描述 守望者在与尤迪安的交锋中遭遇了围杀,被困在一个荒芜的大岛上。 为了杀死守望者,尤迪安开始对这个荒岛施咒,这座岛…...
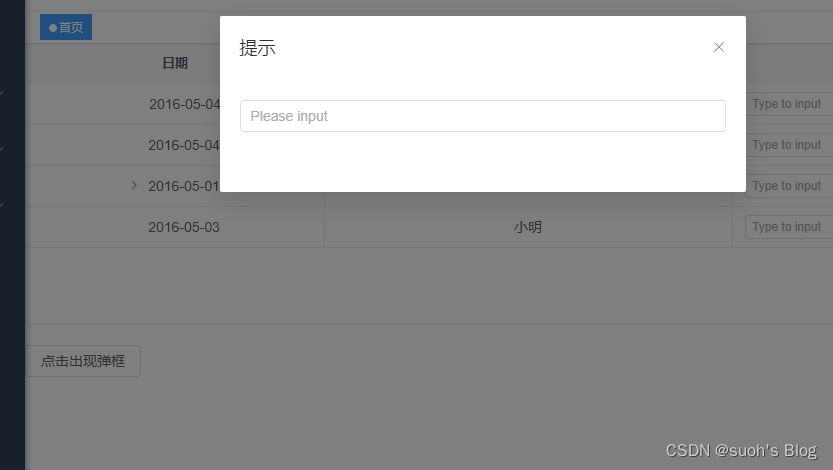
vue3+ts+elementui-plus二次封装弹框
一、弹框组件BaseDialog <template><div classmain><el-dialog v-model"visible" :title"title" :width"dialogWidth" :before-close"handleClose"><!-- 内容插槽 --><slot></slot><template…...

ffmpeg批量分割视频解决视频前几秒黑屏的问题解决
echo 请输入视频地址: set /p fp echo 请输入开始时间: set /p st echo 请输入结束时间: set /p et echo 请输入分片时间: set /p sgt echo 注意:循环范围参数要空格。 for /l %%i in (%st%, %sgt%, %et%) do call :aa…...

nodejs + express 调用本地 python程序
假设已经安装好 nodejs ; cd /js/node_js ; 安装在当前目录的 node_modules/ npm install express --save 或者 cnpm install express --save web 服务器程序 server.js const http require(http); const express require(express); const path require(path); const …...

微信小程序代码优化3个小技巧
抽取重复样式 样式复用 我们会发现很多时候在开发的过程中会存在多个页面中都用到了同样的样式,那么其实之前有提到过,公用样式可以放在app.wxss里面这样就可以直接复用。 如:flex布局的纵向排列,定义在app.wxss里面 .flex-co…...
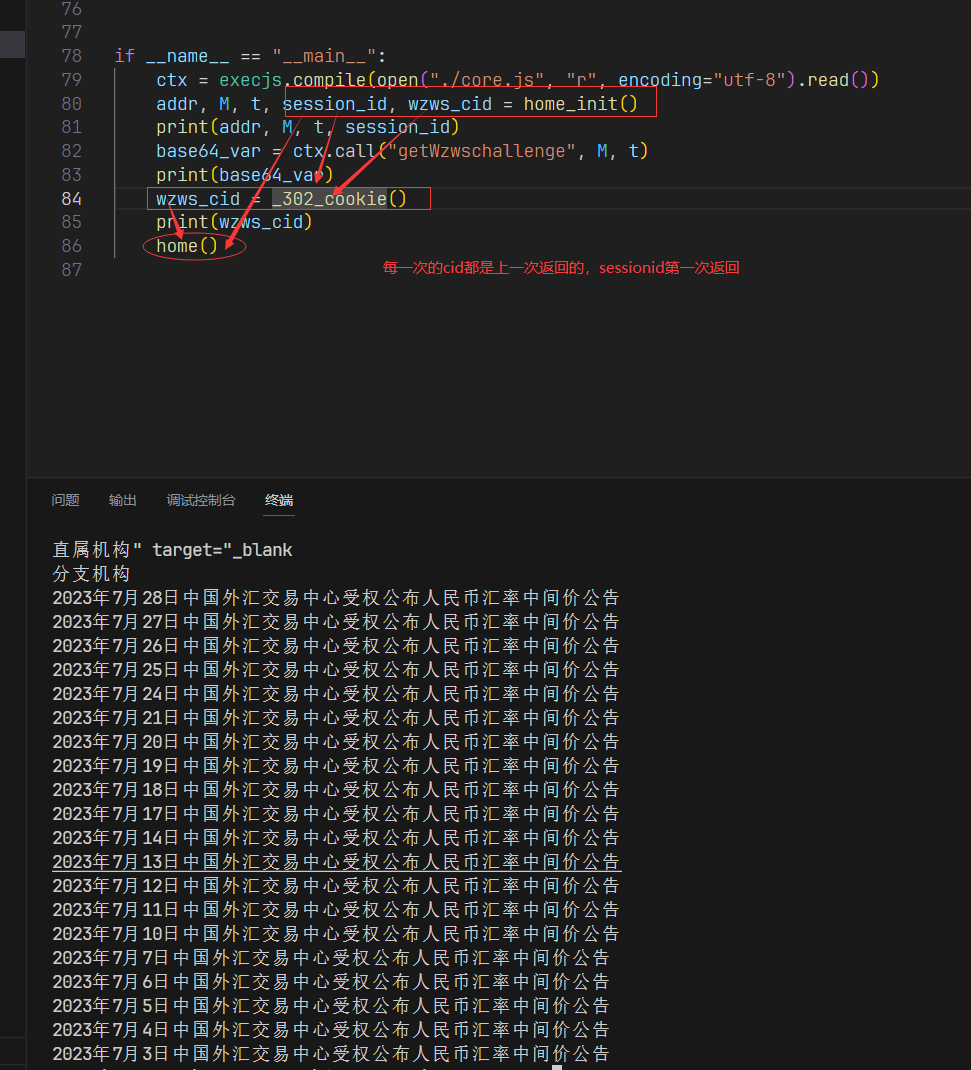
某行动态cookie反爬虫分析
某行动态cookie反爬虫分析 1. 预览 反爬网址(base64): aHR0cDovL3d3dy5wYmMuZ292LmNu 反爬截图: 需要先加载运行js代码,可能是对环境进行检测,反调试之类的 无限debugger 处理办法 网上大部分人说的都是添加cookie来解决。 那个noscript…...

恒运资本:A股、港股全线爆发,沪指突破3300点,恒指重返2万点上方
7月31日,两市股指高开高走,沪指在金融、地产、酿酒等权重板块的带动下一举突破3300点。截至发稿,沪指、深成指、创业板指涨幅均超1%,上证50指数涨近2%。Wind数据显现,北向资金净买入超25亿元。 职业方面,券…...

Rust vs Go:常用语法对比(十二)
题图来自 Rust vs Go in 2023[1] 221. Remove all non-digits characters Create string t from string s, keeping only digit characters 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. 删除所有非数字字符 package mainimport ( "fmt" "regexp")func main() { s : hei…...
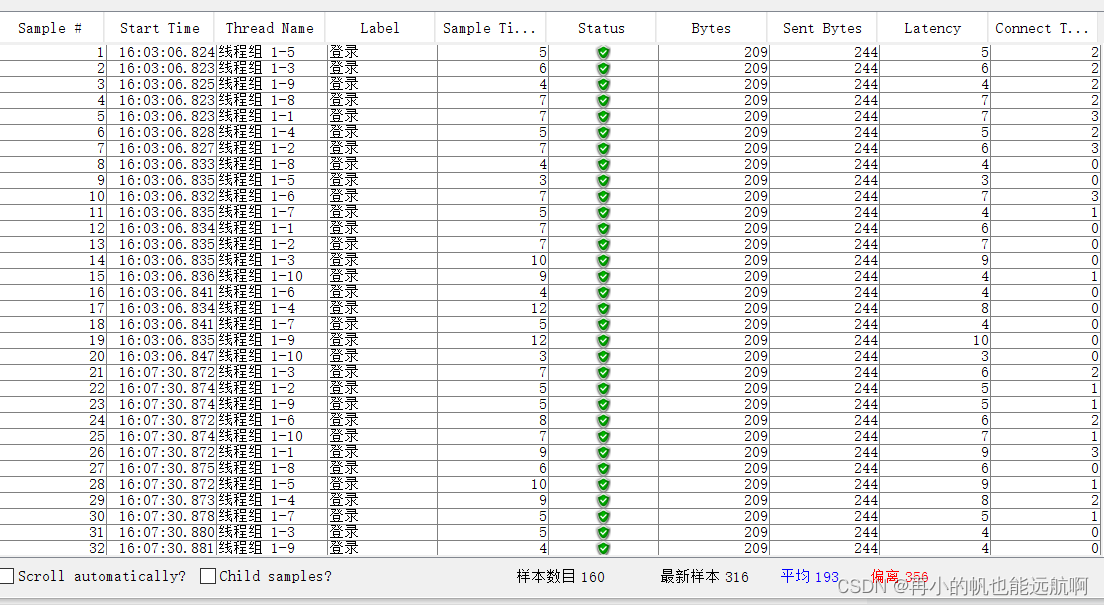
jmeter接口测试、压力测试简单实现
jmeter测试的组件执行顺序: 测试计划—>线程组—>配置元件—>前置处理器—>定时器—>逻辑控制器—>取样器—>后置处理器—>断言—>监听器 组件的作用范围: 同级组件同级组件下的子组件父组件 目前市面上的三类接口 1、基…...
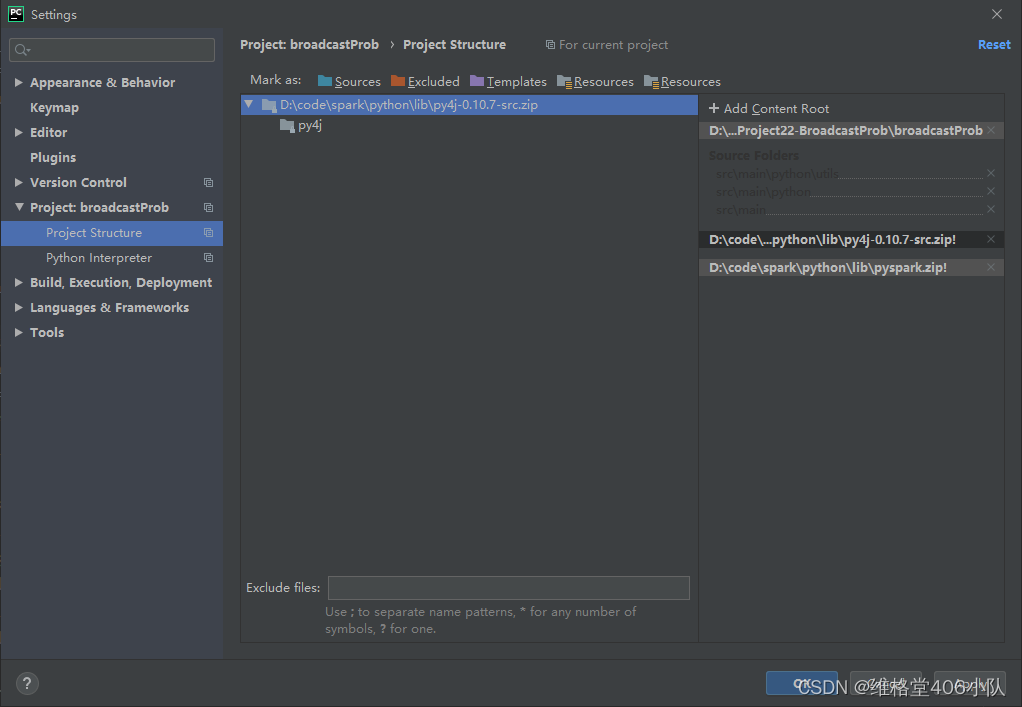
PysparkNote006---pycharm加载spark环境
pycharm配置pyspark环境,本地执行pyspark代码 spark安装、添加环境变量不提了 File-Settings-Project-Project Structure-add content root添加如下两个路径 D:\code\spark\python\lib\py4j-0.10.7-src.zipD:\code\spark\python\lib\pyspark.zip 2023-07-26 阴 于…...
)
19套项目实战系列--Spring Cloud Spring Boot(整套源码)
整套大型项目源码,需要的回复私信:19 ┃ ┣━01.19套项目实战系列 ┃ ┃ ┣━第04套【项目实战】Spring Cloud分布式微服务实战,打造大型自媒体3大业务平台 分布式前后端分离项目分层聚合 养成应对复杂业务的综合技术能力 ┃ ┃ ┃ ┣━1-…...
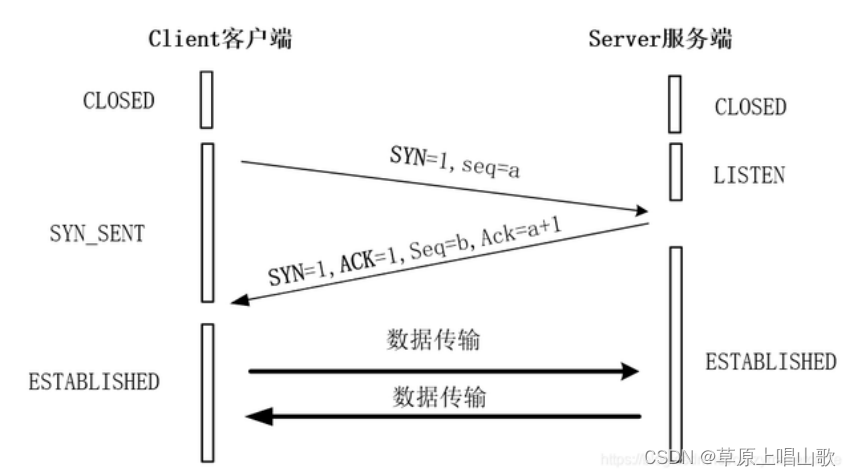
TCP/IP协议详解(二)
目录内容 TCP协议的可靠性 TCP的三次握手 TCP的四次挥手 C#中,TCP/IP建立 三次握手和四次挥手常见面试题 在上一篇文章中讲解了TCP/IP的由来以及报文格式,详情请见上一篇文章,现在接着来讲讲TCP/IP的可靠性以及通过代码的实现。 在TCP首部的…...
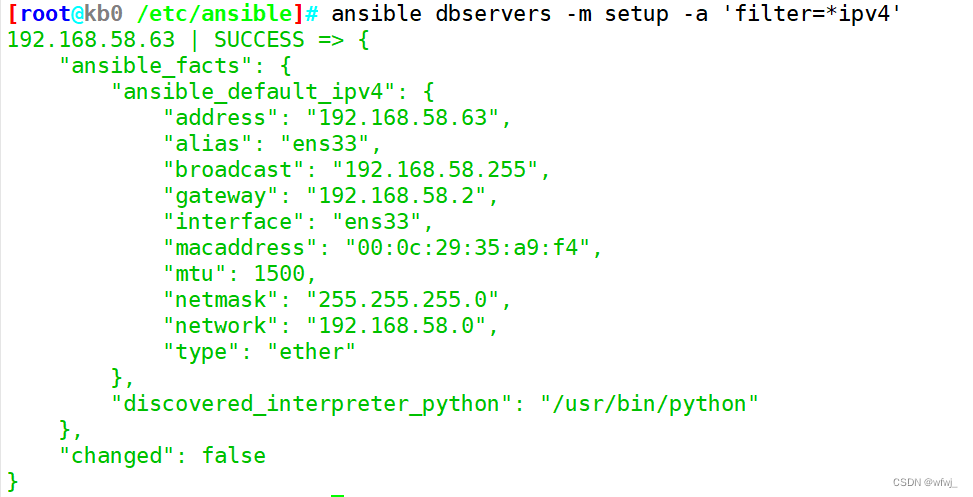
Linux6.2 ansible 自动化运维工具(机器管理工具)
文章目录 计算机系统5G云计算第一章 LINUX ansible 自动化运维工具(机器管理工具)一、概述二、ansible 环境安装部署三、ansible 命令行模块1.command 模块2.shell 模块3.cron 模块4.user 模块5.group 模块6.copy 模块7.file 模块8.hostname 模块9.ping …...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...


