【暑期每日一练】 day10
目录
选择题
(1)
解析:
(2)
解析:
(3)
解析:
(4)
解析:
(5)
解析:
编程题
题一
描述
示例
解析:
代码实现
题二
描述
示例
提示
解析 :
代码实现
总结
选择题
(1)
1、求函数返回值,传入 -1 ,则在64位机器上函数返回( )
int func(int x)
{int count = 0;while (x){count++;x = x&(x - 1);//与运算} return count;
}A: 死循环 B: 64 C: 32 D: 16
答案:C
解析:
x=x&(x-1)这个表达式执行一次就会将x的2进制中最右边的1去掉,在x变成0之前,表达式能执行几次,就去掉几个1,所以这个代码实现了求一个有符号整数二进制补码中1的个数的功能,我们知道-1的补码是全1,而int类型4个字节32位,选C
(2)
2、读代码选结果( )
int count = 0;
int x = -1;
while(x)
{count++;x = x >> 1;
}
printf("%d",count);A: 1 B: 2 C: 32 D: 死循环,没结果
答案:D
解析:
此题一个关键,有符号数右移运算高位是补符号位的,负数的符号位是1,所以x永远不会变为0,是个死循环
(3)
3、下述赋值语句错误的是( )
A: a = (b = (c = 2 , d = 3)) B: i++ C: a/b = 2 D: a = a < a + 1
答案:C
解析:
C选项中a/b是表达式,表达式计算的结果是一个值不能做左值
(4)
4、若有 int w=1, x=2, y=3, z=4; 则条件表达 w < x ? w : y < z ? y : z 的值是( )
A: 1 B: 2 C: 3 D: 4
答案:A
解析:
w<x?w:(y<z?y:z)加个括号应该就好理解了w<x为真,返回w,即表达式的值为1
(5)
5、以下程序运行后的输出结果是( )
int main()
{int a=1,b=2,m=0,n=0,k;k=(n=b<a)&&(m=a);printf("%d,%d\n",k,m);return 0;
}A: 0,0 B: 0,1 C: 1,0 D: 1,1
答案:A
解析:
k=(n=b<a)&&(m=a);这部分的执行顺序如下:先执行n=b<a部分,其中,关系运算符优先级高于赋值运算符,所以先算b<a,得到0,n=0赋值运算的结果将作为括号内表达式的结果,即(n=b<a)&&(m=a)转换成(0)&&(m=a),&&运算前表达式为假,则后面的括号(m=a)不运算,m值还是0,最后,&&的结果是0,即k=0
编程题
题一
描述
写一个函数,求两个整数之和,要求在函数体内不得使用+、-、*、/四则运算符号。
数据范围:两个数都满足 −10≤≤n≤1000
示例
解析:
十进制相加思想: 15+07 , 先计算不考虑进位的相加结果 12 (因为 5+7 的不考虑进位的结果是 2 ,遇 10 进位嘛),然后计算进位 5+7 进位是 10 ,则 10 与 12 再次相加,得到 22 ,进位为 0 ,则计算到此结束。
这里使用二进制求和完成,思想类似,但是二进制计算相加和进位不需要使用 + 符号
二进制相加思想:与十进制相同,先计算不考虑进位的相加结果( 0+0 得 0 , 1+1 进位得 0 , 1+0 得 1 ),使用异或可以取得; 然后计算相加的进位结果(同 1 的位置左移一位即可),使用相与后左移取得。
示例:
5 0101 + 7 0111
不考虑进位的相加结果 0101^0111 -> 0010
相加的进位 0101&0111 -> 0101 因为进位左移得到 1010
1010 + 0010
不考虑进位的相加结果 1010 ^ 0010 -> 1000
相加的进位 1010 & 0010 -> 0010 因为进位左移得到 0100
1000 + 0100
不考虑进位的相加结果 1000 ^ 0100 -> 1100
相加的进位 1000 & 0100 -> 0000 进位为0结束运算
代码实现
int Add(int num1, int num2 ) {while(num2 != 0){ //进位不为0则持续与相加结果进行相加int tmp = num1 ^ num2;//得到每位相加不考虑进位的数据num2 = (num1 & num2) << 1;//同1的位相加则会进位num1 = tmp;} return num1;
}题二
描述
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
示例

提示
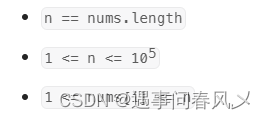
解析 :
numsSize 大小的数组,其中每个元素的数据在 [1, numsSize] 区间之内,解法其实并不复杂,以数组元素的绝对值作为下标,将对应位置的数据置为负数,比如 0 号位置是 3 ,则把 3 号位置的数据重置为负值,等到数组遍历重置完毕,只有缺失的这个数字对应的位置保留正数,其他出现过的数字位置都会是负数, 要注意不要重复设置负数,因为负负得正。
示例
[2, 3, 3, 2, 4] 注意数组10个元素,值为[1-10], 但是访问下标应该在[0-9]之内,因此修改位置下标应该是值-1
0号元素是2,则将1号位置置为对应负值 [2, -3, 3, 2, 4]
1号元素是3,则将2号位置置为对应负值 [2, -3, -3, 2, 4]
2号元素是-3,绝对值为3,将2号位置为负值,但是2号位已经重置过,不需要重置,否则会变正数[2, -3, -3, 2, 4]
3号元素是-2,绝对值为2,将1号位置为负值,但是1号位已经重置过,不需要重置,否则会变正数[2, -3, -3, 2, 4]
4号元素是4,则将3号位置置为对应负值 [2, -3, -3, -2, 4]
遍历数组得到0,4两个位置的数据是大于0的,因为人家数值从1开始,因此+1后得到1, 5两个缺失的数字
代码实现
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize)
{for (int i = 0; i < numsSize; i++){if (nums[abs(nums[i]) - 1] > 0)nums[abs(nums[i]) - 1] = -(nums[abs(nums[i]) - 1]);}int *ret = (int *)malloc(sizeof(int) * (numsSize));*returnSize = 0;for (int i = 0; i < numsSize; i++) {if (nums[i] > 0){ret[*returnSize] = i + 1;*returnSize += 1;}
} return ret;
}总结
关于今日练习讲解到这儿,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下。
相关文章:

【暑期每日一练】 day10
目录 选择题 (1) 解析: (2) 解析: (3) 解析: (4) 解析: (5) 解析: 编程题 题一 …...
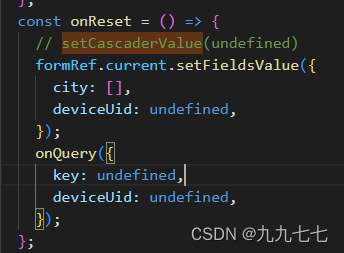
antd中的Cascader级联选择框怎么清空重置React
项目场景: React项目,使用antd中的Cascader级联选择框 问题描述: 通过其他按钮无法重置选择框中的项 原因分析:(对应解决办法一和二) 1、级联选择框的数据默认是根据options绑定的数组中的value值来进行…...
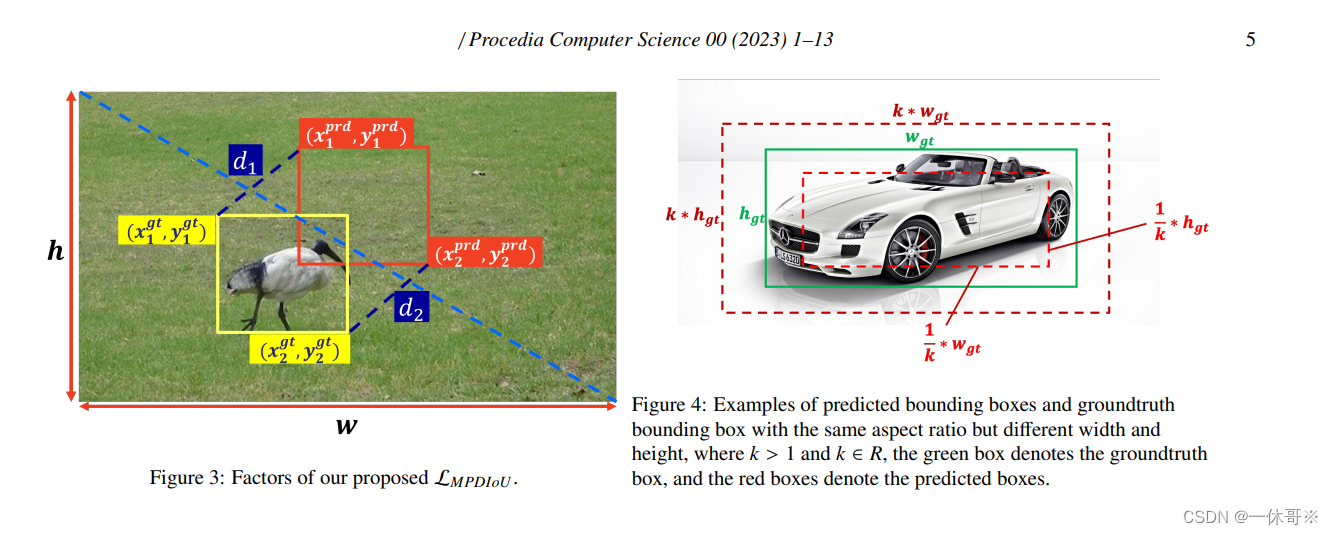
复现YOLOv5改进最新MPDIoU:有效和准确的边界盒回归的损失,打败G/E/CIoU,效果明显!!!
MPDIoU: A Loss for Efficient and Accurate Bounding Box Regression 论文简介MPDIoU核心设计思路论文方法实验部分加入YOLOv5代码论文地址:https://arxiv.org/pdf/2307.07662.pdf 论文简介 边界盒回归(Bounding box regression, BBR)广泛应用于目标检测和实例分割,是目标…...
低代码在数智化时代中的应用
随着科技的发展,企业从生产到经营中海量的数据持续被记录。数据是望远镜,发现完全不同的商业边界;数据是显微镜,判断肉眼察觉不到的消费和生活行为;数据是雷达,帮助企业提前预测未来的行为。 而通过人工智…...
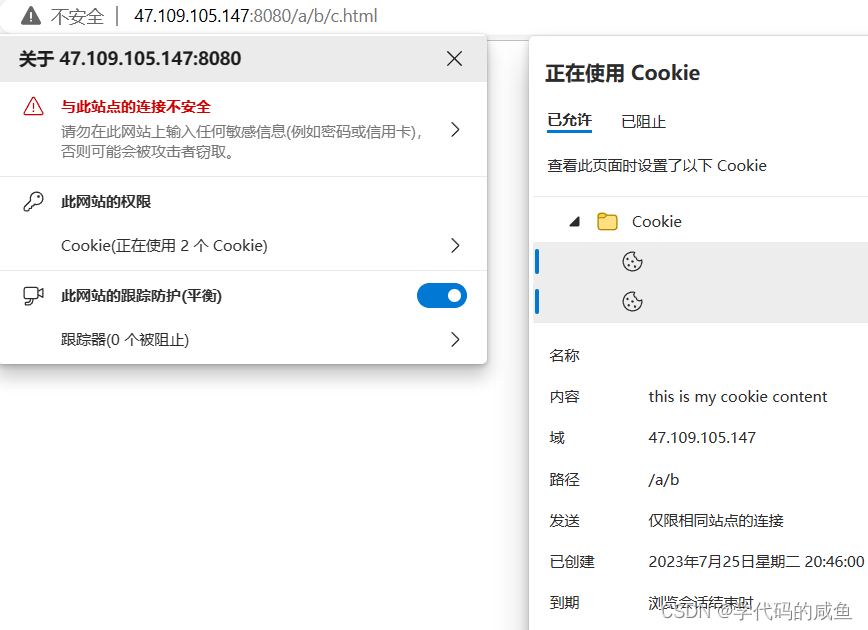
应用层协议——http
文章目录 1. HTTP协议1.1 认识URL1.2 urlencode和urldecode1.3 HTTP协议格式1.3.1 HTTP请求1.3.2 HTTP响应1.3.3 外网测试1.3.4 添加html文件1.3.5 HTTP常见Header1.3.6 GET和POST 1.4 HTTP的状态码1.4.1 301和3021.4.2 代码实现 1.5 Cookie1.5.1 代码验证1.5.2 Cookiesession …...

element-tree-line el-tree 添加结构线 添加虚线
概览:给element组件添加上虚线,通过使用插件element-tree-line 参考连接: 参考别人的博客 安装插件: # npm npm install element-tree-line -S # yarn yarn add element-tree-line -S main.js全局注册引入插件: imp…...

【Lua学习笔记】Lua进阶——函数和闭包
文章目录 函数函数嵌套闭包Closures可变函数函数重载 函数 函数嵌套 function A()print("这里是函数A")return function ()print("返回函数不要起名")end end B A() B()输出: 这里是函数A 返回函数不要起名使用函数嵌套的用法,我…...
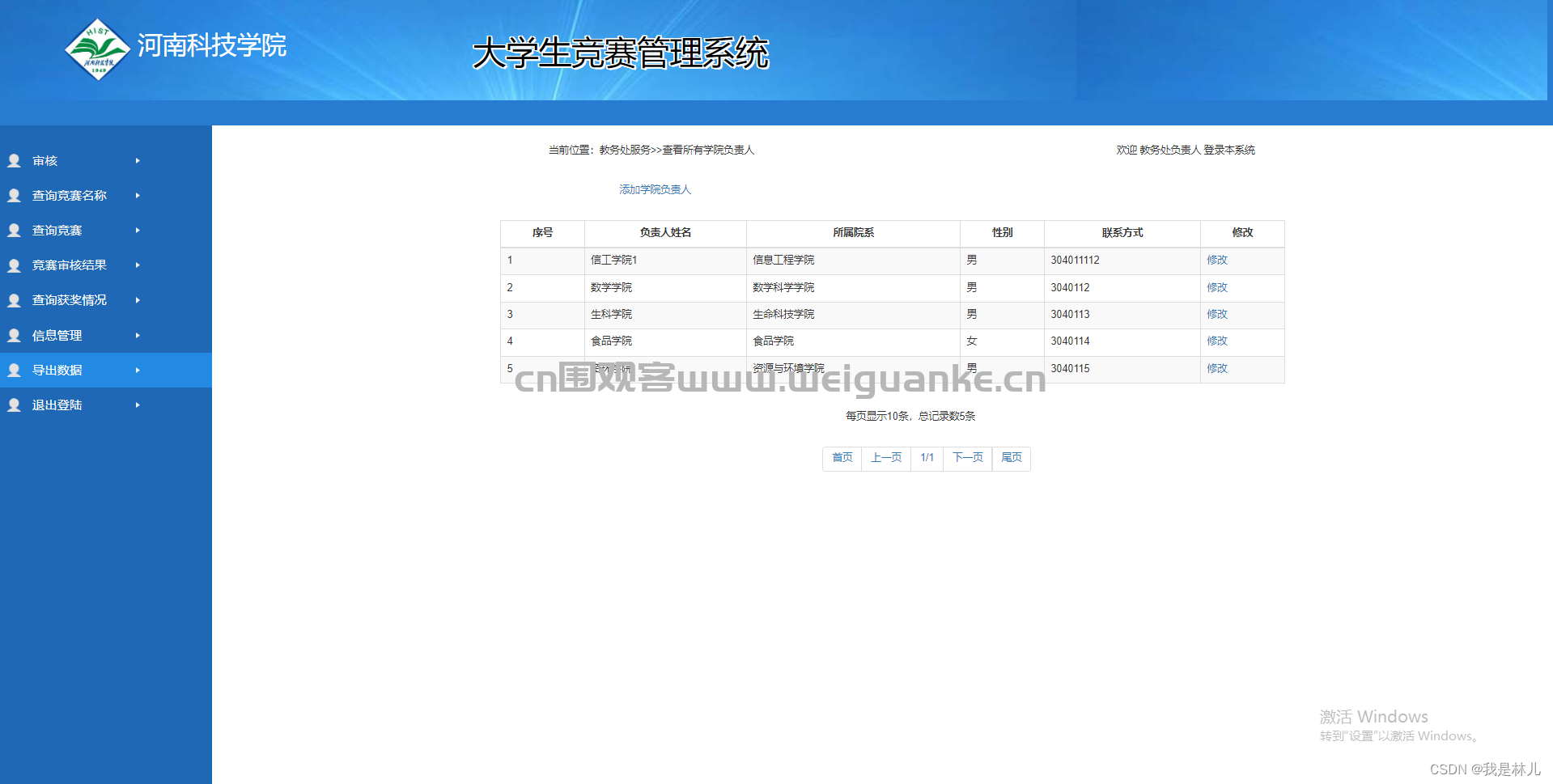
大学生竞赛管理系统springboot比赛报名信息java jsp源代码mysql
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 大学生竞赛管理系统springboot 系统有3权限ÿ…...
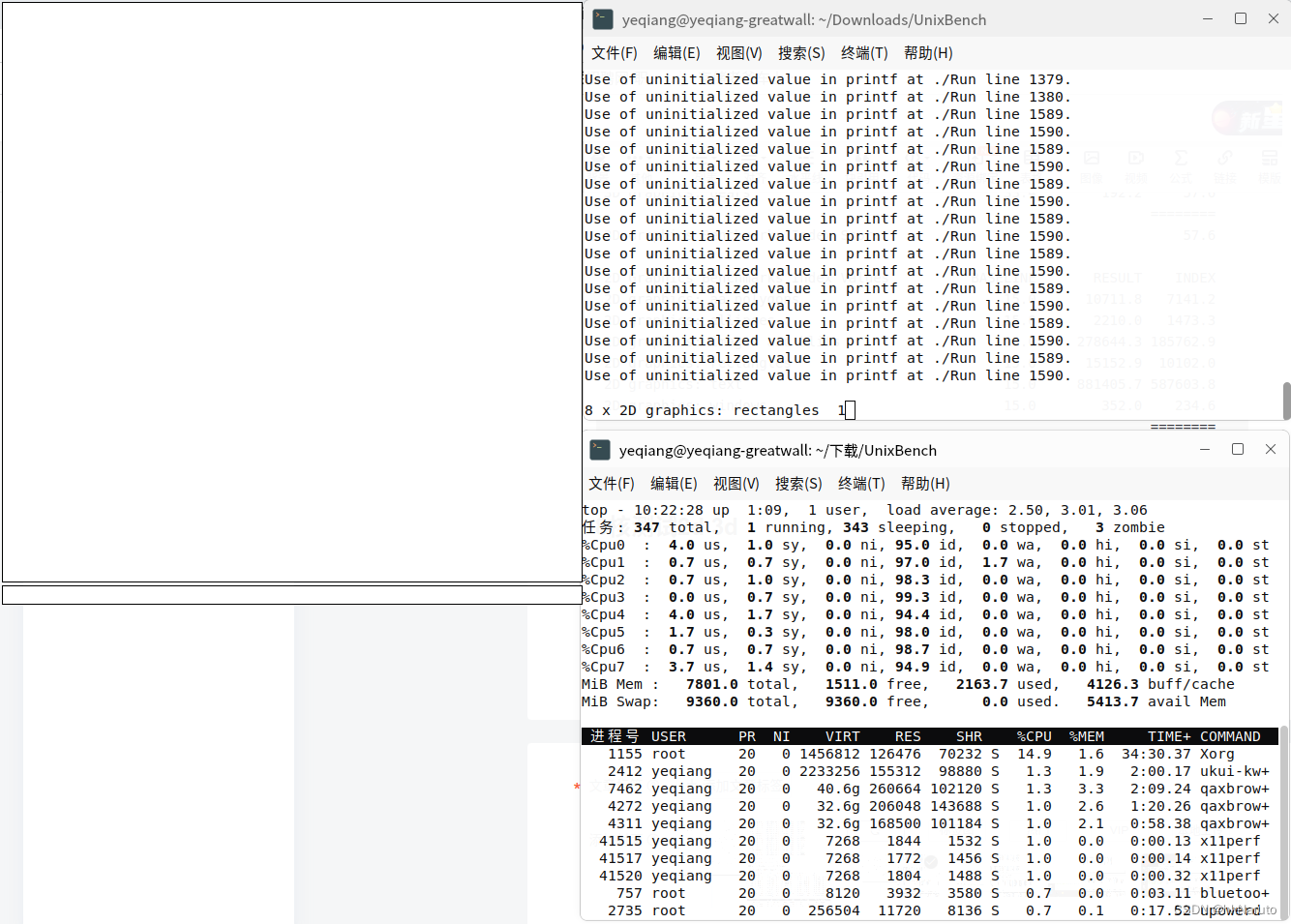
UnixBench 5.1.3 银河麒麟桌面操作系统V10 (SP1) ARM64 aarch64 图形性能测试 2d 3d, glmark2 3d测试
编译 安装libgl sudo apt install libgl-dev yeqiangyeqiang-greatwall:~/Downloads/UnixBench$ sudo apt install libgl-dev [sudo] yeqiang 的密码: 正在读取软件包列表... 完成 正在分析软件包的依赖关系树 正在读取状态信息... 完成 下列软件包…...
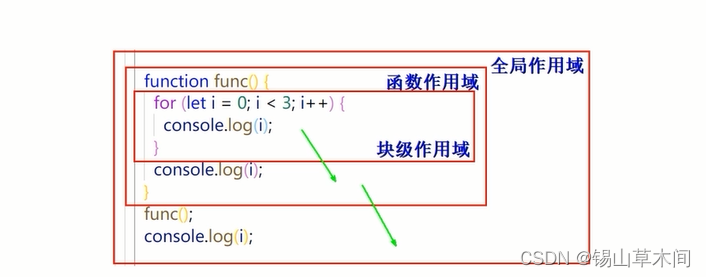
JavaScript高级——ES6基础入门
目录 前言let 和 const块级作用域模板字符串一.模板字符串是什么二.模板字符串的注意事项三. 模板字符串的应用 箭头函数一.箭头函数是什么二.普通函数与箭头函数的转换三.this指向1. 全局作用域中的 this 指向2. 一般函数(非箭头函数)中的this指向3.箭头…...

2023年超越期待的高性能视频剪辑主机推荐| Intel 蝰蛇峡谷测评
1、开箱 蝰蛇峡谷的开箱体验是非常令人兴奋的。首先,打开包装后,你会看到一个精致且高质感的机箱,给人一种专业的感觉。蝰蛇峡谷的外观设计简洁大方,黑色的机箱与红色的Logo相得益彰,展现了其高性能的特点。 在打开机…...

1400*A. Factory
Examples input 1 5 output No input 3 6 output Yes 题意: a 和 m,a 不断加 a%m ,如果 a 有一次能够被 m 整除,则打印 Yes,如果一直循环永远不可能被 m 整除,则打印 No 解析: 可以观…...
OpenHarmony开源鸿蒙学习入门 - 基于3.2Release 应用开发环境安装
OpenHarmony开源鸿蒙学习入门 - 基于3.2Release 应用开发环境安装 基于目前官方master主支,最新文档版本3.2Release,更新应用开发环境安装文档。 一、安装IDE: 1.IDE安装的系统要求 2.IDE下载官网链接(IDE下载链接) …...

Linux 查看服务器内存、CPU、网络等占用情况的命令
1、查看物理CPU个数:cat cat /proc/cpuinfo | grep "physical id" | sort | uniq | wc -l 2、查看服务器CPU内核个数:cat 每个物理CPU中core的个数(即核数) cat /proc/cpuinfo | grep "cpu cores" | u…...

调用webservice导excel文件内容进入数据库
一个早期vb.net写的程序,需要增加功能,要导入excel数据,并按条件显示。 1.数据库端 1.1因为是要把表作为存储过程的输入参数,所以先新建一个数据类型xtabletype create type xtabletype as table(prodid varchar(20),itemid varchar(20),target varchar(150)) 1.2新建…...
*CTF 2023 web jwt2struts 题解wp
jwt2struts 根据题目名字猜测,这题考察jwt和Struts2 包里面果然有一个cookie 验证了,是jwt eyJ0eXAiOiJKV1QiLCJhbGciOiJIUzI1NiJ9.eyJzdWIiOiJ1c2VyIiwiZXhwIjoyMDA2MjI1MjgxfQ.F7vOtdqg48M1DYK4tVZywTipIYDqKfsBSju7ekLSecU 我们的目标应该是把user改…...
使用java实时获取手环、手表的健康数据
吐槽 最近在自研开发一款有关读取健康数据的APP 但是数据来源非常稀少,申请了市面上所有的国内厂商的手环api都被拒了(因为是个人开发) 找了很久发现fitbit有开源的api于是淘了个fitbit的手表开始开发 Web API (fitbit.com) 在上述连接可…...

Maven右侧依赖Dependencies消失
项目右侧的Maven依赖Dependencies突然消失,项目中的注解都出现报错,出现这种情况应该是因为IDEA版本早于maven版本,重新检查项目中的Maven路径,选择File->Settings->搜索Maven,检查Maven home directory…...

100% RNN language model ChatRWKV 相关开源项目
RWKV(读作RwaKuv)借鉴了RNN的移动平均模型(MA),将transformer的 O ( T 2 d ) O(T^2d) O(T2d)复杂度降低到 O ( T d ) O(Td) O(Td),同时保持较好的结果表现。RWKV也是一个开源模型,甚至其介绍主页的html代码都有开源。以…...
ElasticSearch Window Linux部署
文章目录 一、Window 集群部署二、Linux 单节点部署三、Linux 集群部署 一、Window 集群部署 创建 elasticsearch-cluster 文件夹,在内部复制三个elasticsearch服务 修改集群文件目录中每个节点的 config/elasticsearch.yml 配置文件 # -----------------------…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
