MVC乱码问题
@RequestMapping(value = "insert",produces = {"text/html;charset=utf-8"})
//前端响应回去加响应头,解决乱码问题,这个还跟JSP响应头还不一样,这是响应的字符串,纯文本,那个前端的是out.Writer()对象,写到前端。
// 而这个是由异步请求响应到前端,应该不是一个东西了,所以在JSP响应头的那个乱码解决问题,已经对这个没有效果,所以必须加上produces = {"text/html;charset=utf-8"}
//来解决乱码问题,异步请求纯文本乱码问题
//json乱码问题已经由内部MVC自动解决了,就差一个时间问题,时间问题在实体类上面加个注解,然后标注格式与时差来完成时间戳与时间格式字符串的转换。
//jackson以前写的,java转json ,
// 就是五步,第一创建ObjectMapper对象,第二给定日期格式,第三JSON乱码解决问题,第四步把java对象放入这个对象里,第五步调用writeValueAsString方法把java对象转化为json字符串
乱码问题
1.mvc的过滤器 :只能解决请求乱码问题
2.JSP文件的响应头只解决响应对象write方法的 乱码问题
3.异步请求乱码问题
3.1 纯文本乱码问题:@RequestMapping(value = “insert”,produces = {“text/html;charset=utf-8”})
3.2 json字符串乱码问题,由MVC底层自动处理了。
相关文章:

MVC乱码问题
RequestMapping(value "insert",produces {"text/html;charsetutf-8"}) //前端响应回去加响应头,解决乱码问题,这个还跟JSP响应头还不一样,这是响应的字符串,纯文本,那个前端的是out.Writer()对象ÿ…...
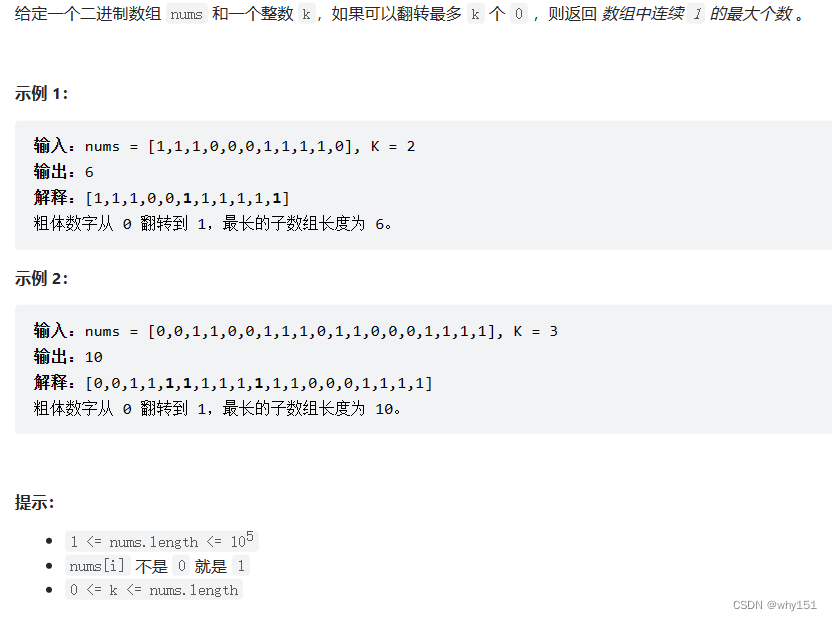
1004. 最大连续1的个数 III
题目描述: 主要思路: 刚看到这个问题首先想到的是二分答案,二分长度,然后利用滑动窗口判断是否可以达成。 class Solution { public:bool find(int x,vector<int> nums, int k){int now0;for(int i0,j0;i<nums.size();…...
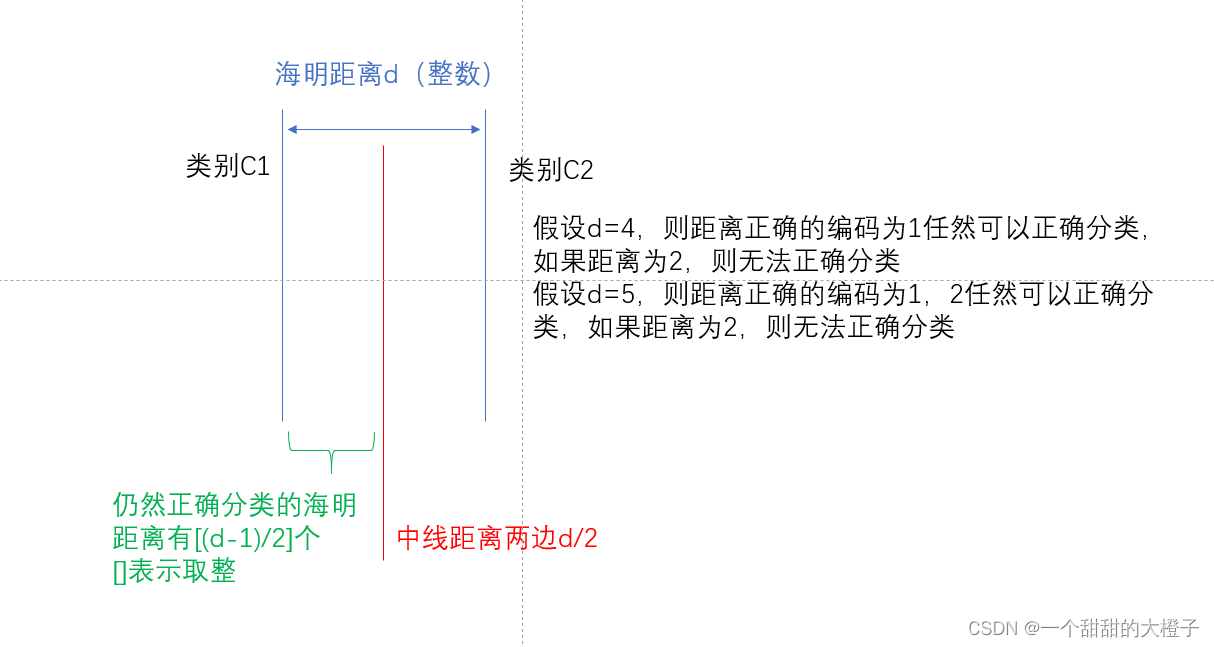
【机器学习】西瓜书学习心得及课后习题参考答案—第3章线性模型
过了一遍第三章,大致理解了内容,认识了线性回归模型,对数几率回归模型,线性判别分析方法,以及多分类学习,其中有很多数学推理过程以参考他人现有思想为主,没有亲手去推。 术语学习 线性模型 l…...
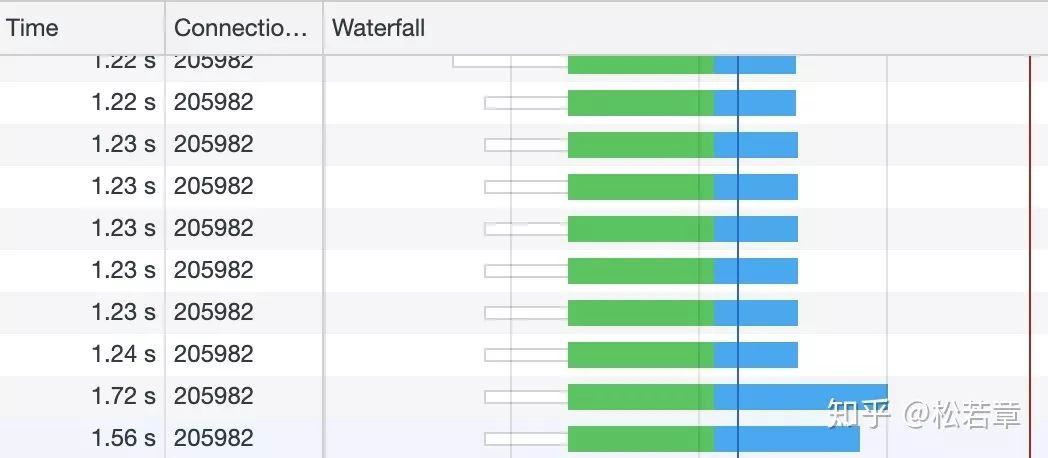
面试官问我:一个 TCP 连接可以发多少个 HTTP 请求?我竟然回答不上来...
一道经典的面试题是从 URL 在浏览器被被输入到页面展现的过程中发生了什么,大多数回答都是说请求响应之后 DOM 怎么被构建,被绘制出来。但是你有没有想过,收到的 HTML 如果包含几十个图片标签,这些图片是以什么方式、什么顺序、建…...

树莓派Pico|RP2040|官方文档|在MS Windows上构建“Hello World”及环境配置
9.2. 在MS Windows上构建 在Microsoft Windows 10或Windows 11上安装工具链与其他平台有些不同。然而安装后,RP2040的构建代码基本类似。 警告 官方不支持在Windows 7或8上使用Raspberry Pi Pico,但在Windows 7或8上可以使其工作。 9.2.1. 安装工具…...

全球公链进展| 2023/7/31
一周速览 过去一周,明星项目动态如下: 第114次以太坊核心开发者共识会议:Devnet #8 最早下周推出 Layer2网络Shibarium跨链桥已上线公开测试 Optimism 推出「Law of Chains」v0.1 版本 Sui 通过 SIP#6 ,允许开发人员构建流动…...
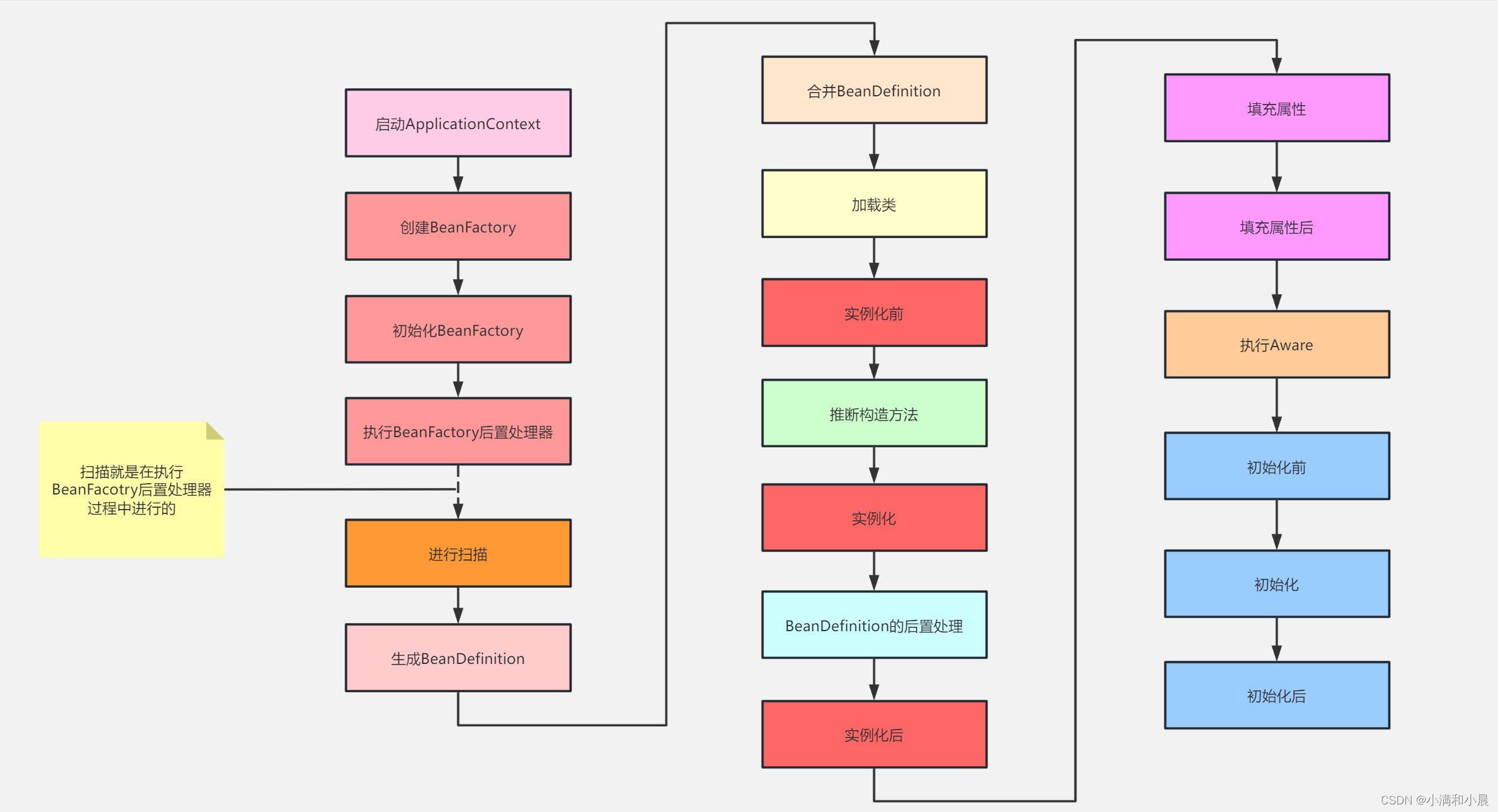
Spring源码(三)Spring Bean生命周期
Bean的生命周期就是指:在Spring中,一个Bean是如何生成的,如何销毁的 Bean生命周期流程图 1、生成BeanDefinition Spring启动的时候会进行扫描,会先调用org.springframework.context.annotation.ClassPathScanningCandidateCompo…...
【iOS】Cydia Impactor 错误:file http.hpp; line:37; what: _assert(code == 200)
Cydia Impactor 报错,信息如下 file http.hpp; line:37; what: _assert(code 200)解决方案:Cydia Impactor 已被弃用,切换到sideloadly 即可,亲测成功,并且支持双重验证登录 csdn备份地址 HERE...
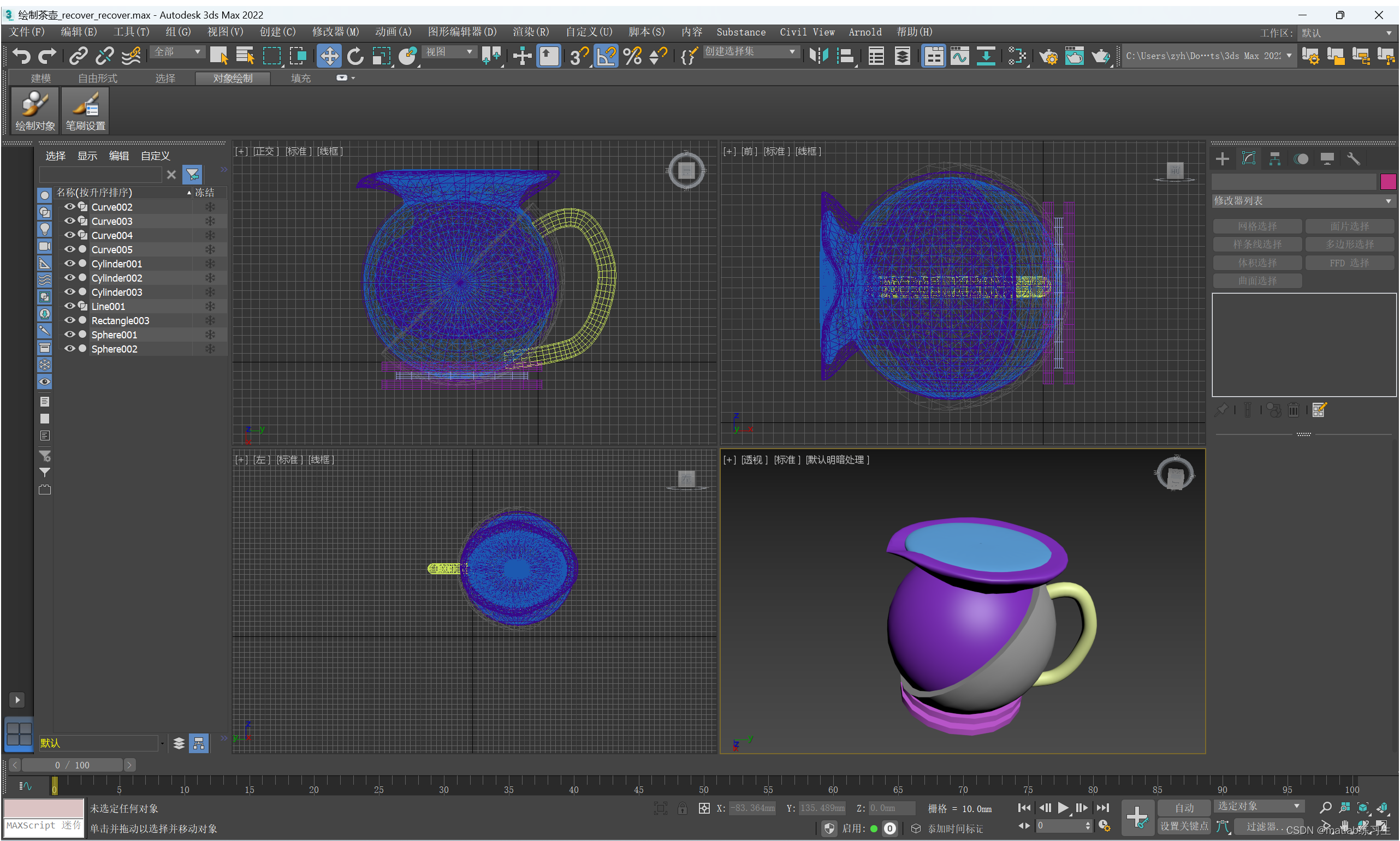
3ds MAX绘制茶壶
综合一下之前的内容画个茶壶 长方形,然后转化为可编辑多边形,添加节点并设置圆角,如下图 车削生成一个圆环,其实这一步也可以用一个圆柱体和两个圆角圆柱体解决 效果如下: 茶壶的底座绘制好了 接下来是茶壶的上半边 …...

【element-plus】 table表格每行圆角解决方案 element也通用
系列文章目录 【Vue3ViteTselement-plus】使用tsx实现左侧栏菜单无限层级封装 前言 我们在使用element-plus或element 的table时是否有时UI给到的UI效果是如下面这样的,但是我们翻遍了组件库的文档 调整了很多次样式 发现在 左右侧栏固定的时候 普通的方法是完全…...
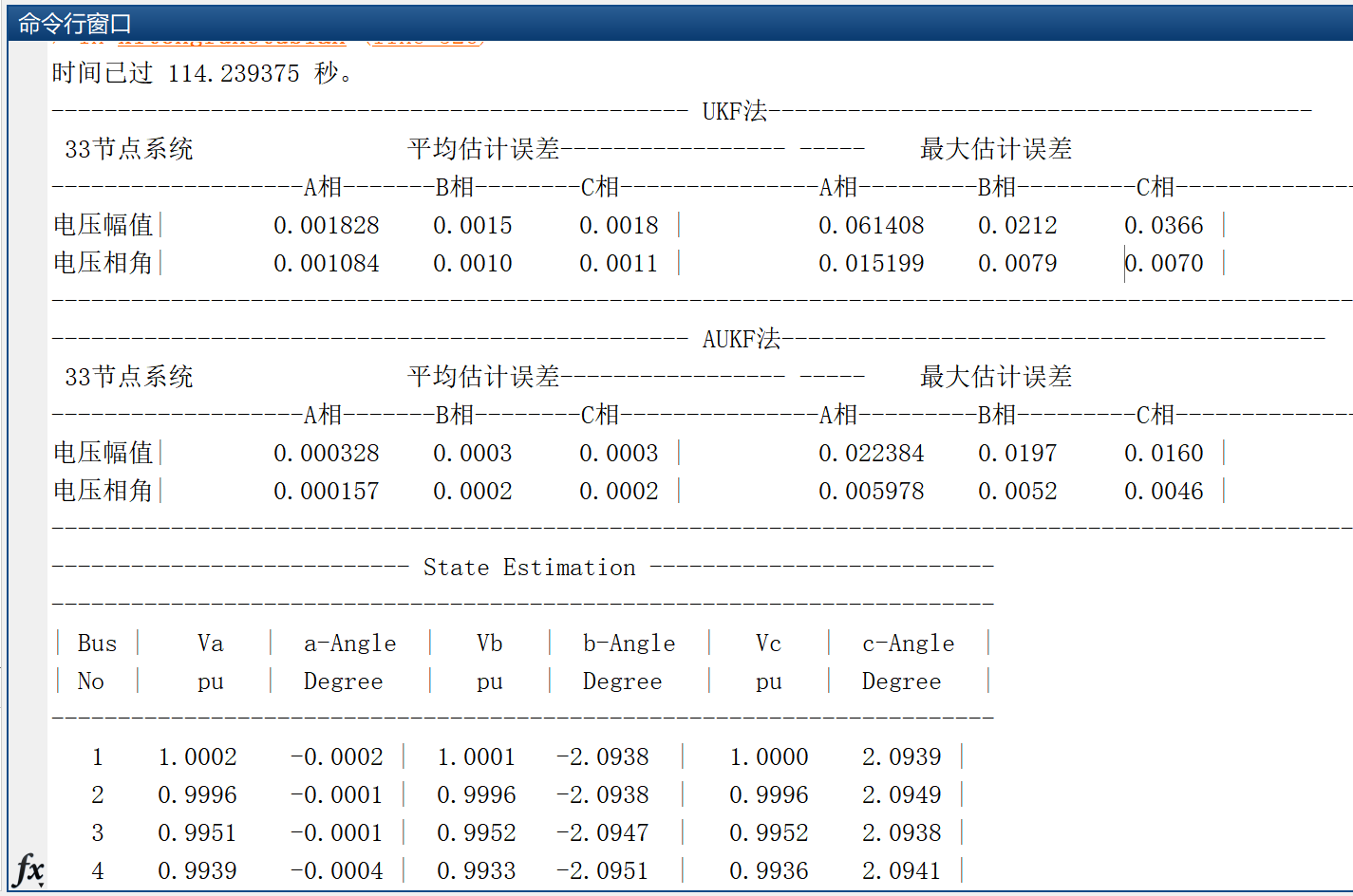
【状态估计】基于UKF、AUKF的电力系统负荷存在突变时的三相状态估计研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

webstorm格式化代码后单引号转成了双引号
webStorm格式化js代码时单引号变成了双引号,问题如下: 格式化前: 格式化后: 解决办法: window: File -> Settings -> Editor -> Code Style -> Javascript; mac: webStorm -> Preference …...

在langchain中使用带简短知识内容的prompt template
简介 langchain中有个比较有意思的prompt template叫做FewShotPromptTemplate。 他是这句话的简写:“Prompt template that contains few shot examples.” 什么意思呢?就是说在Prompt template带了几个比较简单的例子。然后把这些例子发送给LLM&…...

java医院电子病历系统源码:云端SaaS服务 前后端分离模式开发和部署
电子病历系统是什么? 电子病历是指医务人员在医疗活动过程中,使用医疗机构信息系统生成的文字、符号、图表、图形、数据、影像等数字化信息,并能实现存储、管理、传输和重现的医疗记录,是病历的一种记录形式。 医院通过电子病历以电子化方式记录患者就诊的信息&…...

【Golang 接口自动化01】使用标准库net/http发送Get请求
目录 发送Get请求 响应信息 拓展 资料获取方法 发送Get请求 使用Golang发送get请求很容易,我们还是使用http://httpbin.org作为服务端来进行演示。 package mainimport ("bytes""fmt""log""net/http""net/url&qu…...
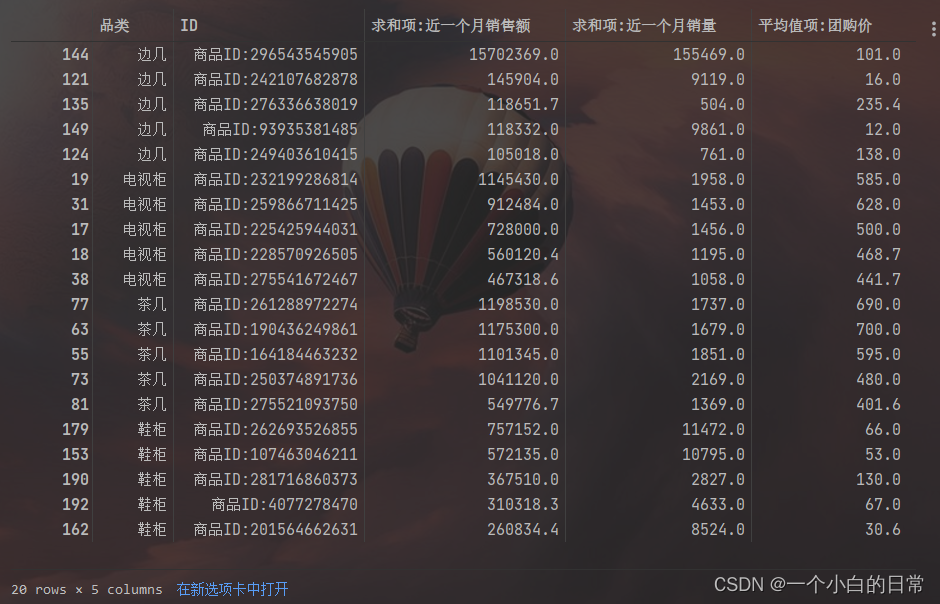
Excel透视表与python实现
目录 一、Excel透视表 1、源数据 2、数据总分析 3、数据top分析 二、python实现 1、第一张表演示 2、第二张表演示 一、Excel透视表 1、源数据 1)四个类目,每类50条数据 2)数据内容 2、数据总分析 1)选择要分析的字段&…...
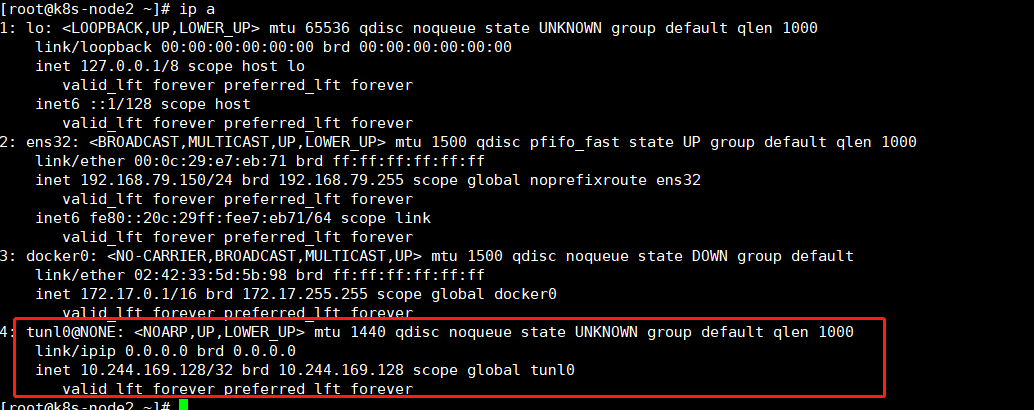
二级制部署kubernetes(1.20)
😘作者简介:一名运维工作人员。 👊宣言:人生就是B(birth)和D(death)之间的C(choise),做好每一个选择。 🙏创作不易,动动小…...

云曦暑期学习第二周——文件上传漏洞
1.文件上传 1.1原理 一些web应用程序中允许上传图片、视频、头像和许多其他类型的文件到服务器中。 文件上传漏洞就是利用服务端代码对文件上传路径变量过滤不严格将可执行的文件上传到一个到服务器中 ,再通过URL去访问以执行恶意代码。 1.2为什么存在文件上传漏…...

软件测试右移的意义与关键点
测试右移是将测试延伸到研发阶段之后的阶段,一般在产品发布上线后进行的测试,包括在线测试,在线监控和日志分析,甚至包括α测试、β测。测试右移描述的是软件测试工作重心的转变,而不是某项具体的测试技术。 测试右移的含义 测试…...
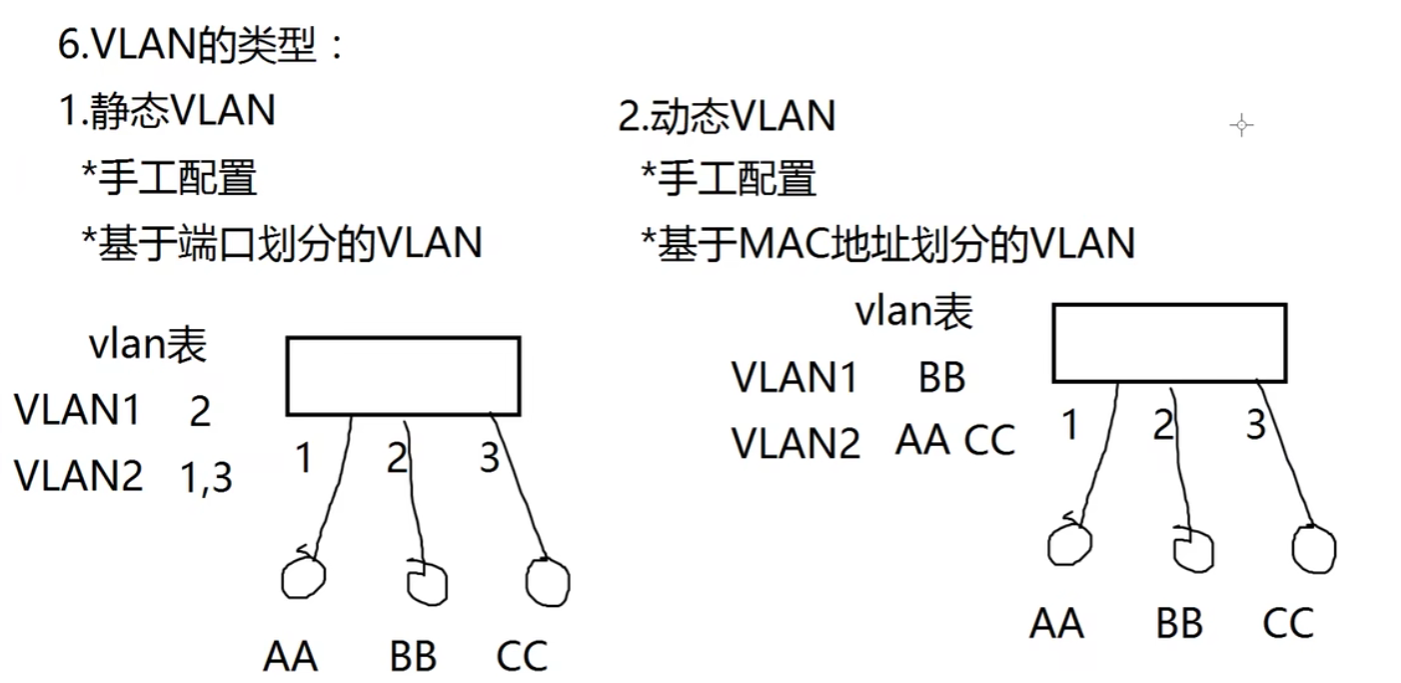
VLAN原理(Virtual LAN 虚拟局域网)
VLAN(Virtual LAN 虚拟局域网) 1、广播/广播域 2、广播的危害:增加网络/终端负担,传播病毒, 3、如何控制广播?? 控制广播隔离广播域 路由器物理隔离广播 路由器隔离广播缺点&…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...
