2,认识N(logN)的排序【p3】
认识N( logN} 的排序
- 2.1归并排序
- 2.1.1代码实现归并排序
- 2.1.1.1自己c++实现归并排序
- 2.1.1.2gptc++实现归并排序
- 2.1.1.3总结
- 2.1.1.4比较行为
- 2.1.2归并排序使用master公式
- 2.1.3归并排序的扩展
- 2.1.3.1小和问题
- 2.1.3.2逆序对问题
- 2.2快排、荷兰国旗问题
- 2.2.1问题一
- 2.2.2问题二(荷兰国旗问题)
- 2.2.2.1快排问题1.0
- 2.2.2.2快排问题2.0
- 2.2.2.3快排问题3.0
2.1归并排序
时间复杂度O(N*logN),额外空间复杂度O(N)
整体就是一个简单递归,左边排好序,右边排好序,让其整体有序
让其整体有序的过程里用了排外序方法
利用master公式来求解时间复杂度
归并排序的实质
二分,左边排好序,右边排好序,左1和右1比较,小的写入新内存,(如右1小,写入右1),左1和右2比较,(如右2小,写入右2),左1和右3比较,(如左1小,写入左1),此时新内存中为(右1,右2,左1),左2和右3比较……

2.1.1代码实现归并排序
2.1.1.1自己c++实现归并排序
自己实现c++代码
#include<iostream>
#include<vector>
#include<set>
#include<algorithm>
void print01(int val)
{std::cout << val << " ";
}
void test01()
{std::vector<int> Arr = { 5,6,9,4,2,3,7,5,6,8 };int length = Arr.size();std::multiset<int>Up;std::multiset<int>Down;if (length % 2 == 1){for (int i = 0; i < (length + 1) / 2; i++){std::vector<int>::iterator it = Arr.end()-1;Up.insert(*it);Arr.pop_back();}for (int j = 0; j < (length - 1) / 2; j++){std::vector<int>::iterator it = Arr.end()-1;Down.insert(*it);Arr.pop_back();}}else{for (int i = 0; i < length / 2; i++){std::vector<int>::iterator it = Arr.end()-1;Up.insert(*it);Arr.pop_back();}for (int i = 0; i < length / 2; i++){std::vector<int>::iterator it = Arr.end()-1;Down.insert(*it);Arr.pop_back();}}std::vector<int>End;for (int q = 0; q < length; q++){std::multiset<int>::iterator it1 = Up.begin();std::multiset<int>::iterator it2 = Down.begin();if (Up.size() != 0 && Down.size() != 0){if (*it1 < *it2){End.push_back(*it1);Up.erase(it1);}else{End.push_back(*it2);Down.erase(it2);}}else if(Up.size() != 0 || Down.size() != 0){if (Up.size() != 0){End.push_back(*it1);Up.erase(it1);}else{End.push_back(*it2);Down.erase(it2);}}else{break;}}for_each(End.begin(), End.end(),print01);
}
int main()
{test01();system("pause");return 0;
}
2.1.1.2gptc++实现归并排序
chatgpt实现
#include<iostream>
#include<set>
#include<algorithm>
#include<vector>void print01(int val)
{std::cout << val << " ";
}void test01()
{std::vector<int> Arr = { 5,6,9,4,2,3,7,5,6,8 };std::multiset<int> Up, Down;int length = Arr.size();int halfLength = (length + 1) / 2;for (int i = 0; i < halfLength; i++){Up.insert(Arr.back());Arr.pop_back();}for (int i = 0; i < halfLength; i++){Down.insert(Arr.back());Arr.pop_back();}std::vector<int> End;while (!Up.empty() && !Down.empty()){if (*Up.begin() < *Down.begin()){End.push_back(*Up.begin());Up.erase(Up.begin());}else{End.push_back(*Down.begin());Down.erase(Down.begin());}}// 处理剩下的元素for (const auto& val : Up){End.push_back(val);}for (const auto& val : Down){End.push_back(val);}std::for_each(End.begin(), End.end(), print01);
}int main()
{test01();std::system("pause");return 0;
}
2.1.1.3总结
总结自己实现和gpt实现,给予gpt的要求是使用归并排序,减少代码行数
gpt没有使用迭代器来接收 Arr 中的值,将迭代器 it 初始化为 Arr 的最后一个元素的迭代器。而是直接使用Arr的迭代器begin
2.1.1.4比较行为
选择排序、冒泡排序、插入排序浪费了大量的比较行为
而归并排序虽然也进行了大量的比较,但是归并行为有效地利用对比,因为每一次比较行为都变成了有序的东西(有结果)
2.1.2归并排序使用master公式
master公式
T(N)=a* T(N/b)+O(N^d)
log(b,a)>d -> 复杂度为 O(N^log(b,a))
log(b,a)=d -> 复杂度为 O(N^d *logN)
log(b,a)< d -> 复杂度为 O(N^d)
logba<d 的时间复杂度O(Nd)
logba>d 的时间复杂度O(N^logb a )
logba==d 的时间复杂度O(Nd *logN)
上面例子中
T(N)=2T(N/2)+O(N),符合master公式
a=2,b=2,d=1
log22==1,所以时间复杂度为O(N)
2.1.3归并排序的扩展
小和问题和逆序对问题
2.1.3.1小和问题
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和,求一个数组的小和
例:[1,3,4,2,5]1左边比1小的数,没有;3左边比3小的数,1;4左边比4小的数,1、3;2左边比2小的数,1;5左边比5小的数,1、3、4、2;所以小和为1+1+3+1+1+3+4+2=16
正常情况下时间复杂度为O(N2)
找寻更快的方法:
[1,3,4,2,5]1右边有4个数比1大14=4,3右边两个数比3大32=6,4右边1个数比4大14=4,2右边1个数比2大21=2;4+6+4+2=16
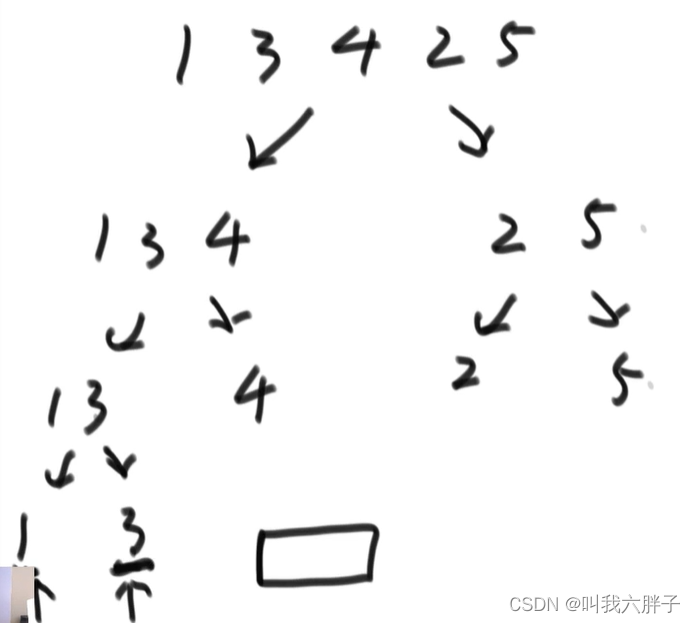
1,3对比产生1个1。返回排序13(排序,从小到大)
1,4对比产生1个1,3。4对比产生1个3,1,3,4.返回排序134
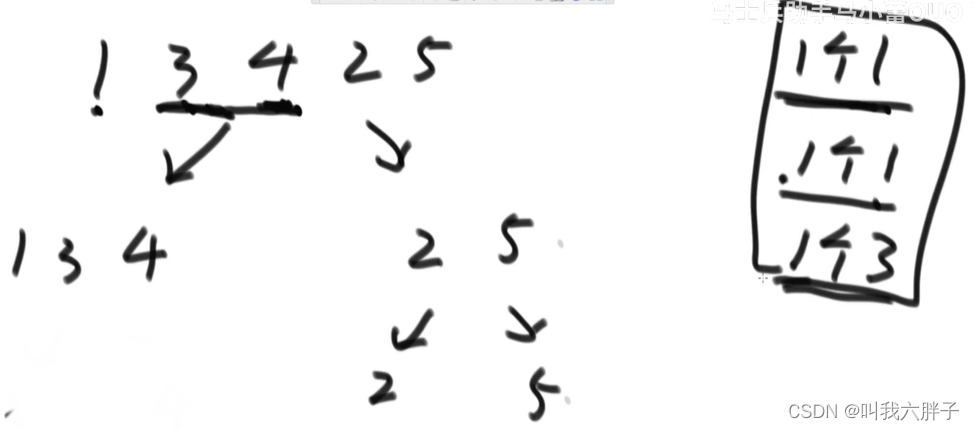
2,5对比产生1个2,返回排序25

134中指向1,25中指向2,对比产生2个1,拷贝1
134中指向3,25中指向2,对比3大,拷贝2,25中指向5,对比产生1个3,拷贝3
134中指向4,25中指向2,对比4大,25中指向5,对比产生1个4,拷贝4,拷贝5
12345
小和1+1+3+2+2+3+4=16
1和2对比产生的2个1不是通过遍历找到的2,而是直接通过下标begin() 和end()找到
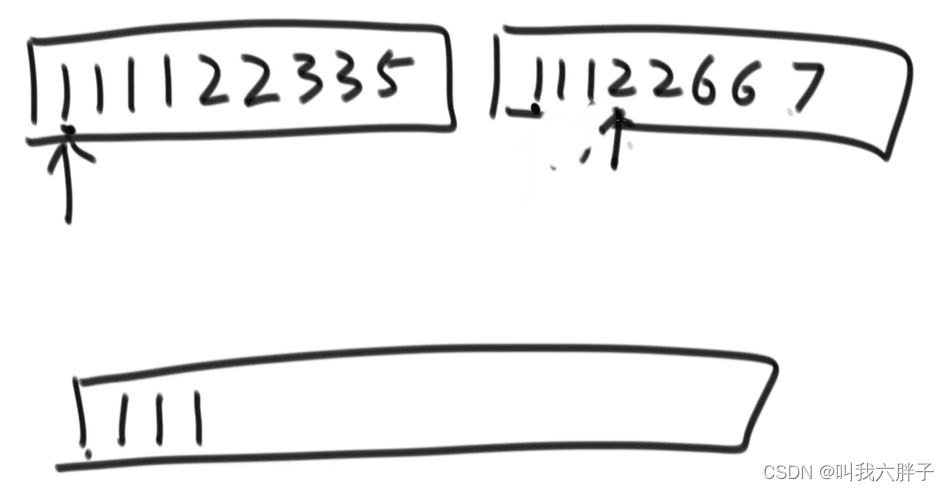
如图情况左右相对,一定要先拷贝右组的数,而不是左组
2.1.3.2逆序对问题
在一个数组中,左边的数如果比右边的数大,则折两个数构成一个逆序对,请打印所有逆序对
例:3,2,4,5,0
32,30,20,40,50
2.2快排、荷兰国旗问题
2.2.1问题一
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。要求额外空间复杂度0(1),时间复杂度0(N)
35674358 num=5
准备一个变量i
情况a,[i]<=num,[i]和<=区的下一个数交换,<=区右扩,i++
情况b,[i]>num,i++
3和num5比较,num5大,情况a执行
5和num5比较,等于num5,情况a执行
6和num5比较,6大,情况b执行
……
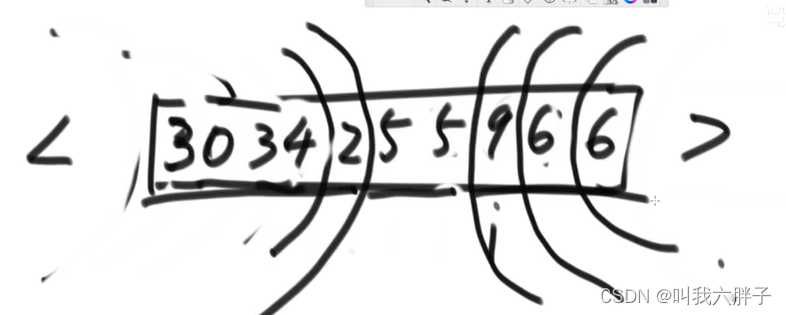
2.2.2问题二(荷兰国旗问题)
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边。要求额外空间复杂度0(1),时间复杂度O(N)
35674358 num=5
准备一个变量i
情况a,[i]<num,[i]和<区的下一个数交换,<区右扩,i++
情况b,[i]>num,[i]和>区的上一个数交换,>区左扩,i不动
情况c,[i]==num,i++
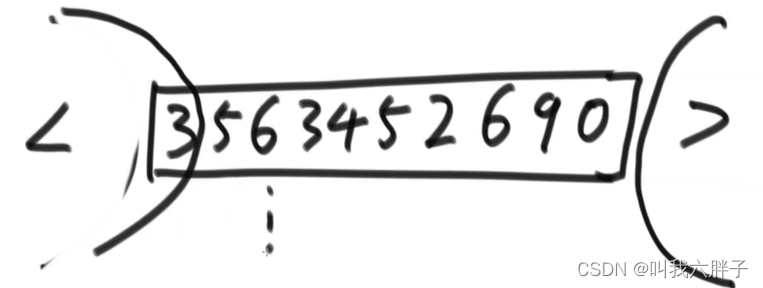
2.2.2.1快排问题1.0
时间复杂度O(N2)
在一串数里,拿最后一个数作为num,<=num放左边,>=num放右边,num和>=num区域的第一个数做交换。再次重复,取新的最后一个数num
2.2.2.2快排问题2.0
时间复杂度O(N2)
最好的情况为T(N)=2T(N/2)+O(N) , 时间复杂度为O(N*logN)
最坏的情况没有左侧部分或右侧部分,时间复杂度O(N2)
在一串数里,拿最后一个数作为num,<num放左边,>num放右边,==num放中间,最后一个数和>5区域第一个数交换。在<num,>num区域做递归
分析:
快排2.0比快排1.0稍快,因为快排2.0一次搞定一批数
划分值越靠近两侧,复杂度越高;划分之越靠近中间,复杂度越低
可以轻而易举的举出最差的例子,所以不改进的快速排序时间复杂度为O(N^2)
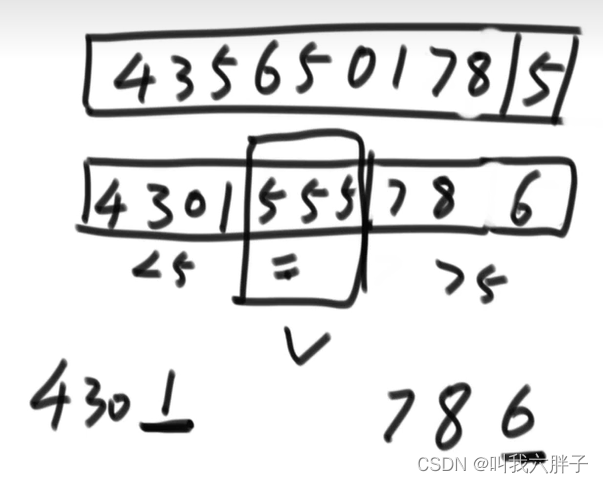
4356501785,取尾数5为num值,排序出三个区域
<5 ,=5 ,>5 5
尾数5和>5区域的第一个数互换
<5 (4301),=5(555) ,>5(786)
4301取尾数1,排序出三个区域
<1 (0),=1 (),>1(43),1
0 1 43
43取尾数3,排出三个区域……
786取尾数6,排序出三个区域
<6 () ,=6 () ,>6(78), 6
6 78
78取尾数8,排出三个区域……
2.2.2.3快排问题3.0
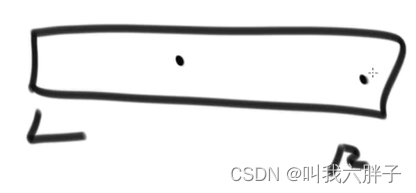
L到R位置上,随机取一个数,和最后一个数交换,然后用此数做划分
原理:
有可能
T(N)=T(N/5)+T(4/5*N)+O(N)
T(N)=T(N/3)+T(2N/3)+O(N)
T(N)=2T(N/2)+O(N)
T(N)=T(4N/5)+T(N/5)+O(N)
…………
所有情况都是等概率1/n的,所以汇总所有可能,把所有式子求概率累加,再求数学长期期望,得出结果O(N * logN)
空间复杂度:O(logN)
相关文章:

2,认识N(logN)的排序【p3】
认识N( logN} 的排序 2.1归并排序2.1.1代码实现归并排序2.1.1.1自己c实现归并排序2.1.1.2gptc实现归并排序2.1.1.3总结2.1.1.4比较行为 2.1.2归并排序使用master公式2.1.3归并排序的扩展2.1.3.1小和问题2.1.3.2逆序对问题 2.2快排、荷兰国旗问题2.2.1问题一2.2.2问题二(荷兰国旗…...

华为机考--服务失效判断--带答案
新2023年华为OD真题机考题库大全-带答案(持续更新)or2023华为OD统一考试(AB卷)题库清单-带答案(持续更新) 题目描述 某系统中有众多服务,每个服务用字符串(只包含字母和数字,长度<…...
C++对C的加强(全)
目录 C对C的加强 命名空间 为什么要使用命名空间 怎么使用命名空间 命名空间的定义 命名空间的使用 使用域解析符 :: 使用using声明 内联命名空间 嵌套命名空间 随时将新的成员加入命名空间 命名空间中 函数的声明和实现分开 无名命名空间 命名空间取别名 使用u…...

ES6及以上新特性
ES6(ECMAScript 2015)及以上版本引入了许多新特性,每个版本都有不同的增强和改进。以下是 ES6 及以上版本的新特性的详细描述: ES6(ECMAScript 2015): let 和 const 声明:引入块级作…...

伦敦金在非农双向挂单
对伦敦金投资有一定经验的投资者都知道,在非农时期,伦敦金市场会出现很大的波动,那么我们如何才能抓住这些波动呢?答案是很难的。但是,有些投资者在多年实践中发明了一种双向挂单的方法,这里和大家一切分享…...
))
【C语言】—— __attribute__((fallthrough))
__attribute__((fallthrough)) 是一个在编译器中使用的特性,用于指示在 switch 语句中的 case 标签中故意省略 break 语句时的意图。它告诉编译器,故意省略 break 是有意为之,而不是出现了错误或遗漏。 当使用 switch 语句时,通常…...

【深度学习】生成对抗网络Generative Adversarial Nets
序言 本文是GAN网络的原始论文,发表于2014年,我们知道,对抗网络是深度学习中,CNN基础上的一大进步; 它最大的好处是,让网络摆脱训练成“死模型”到固定场所处去应用,而是对于变化的场景…...

【深度学习】从现代C++中的开始:卷积
一、说明 在上一个故事中,我们介绍了机器学习的一些最相关的编码方面,例如 functional 规划、矢量化和线性代数规划。 本文,让我们通过使用 2D 卷积实现实际编码深度学习模型来开始我们的道路。让我们开始吧。 二、关于本系列 我们将学习如何…...

金融数学方法:蒙特卡洛模拟
1.方法介绍 蒙特卡洛模拟是一种基于概率和统计的数值计算方法,用于解决各种复杂问题。它以概率统计为基础,通过随机抽样和重复实验的方式进行模拟,从而得到问题的近似解。它的基本思想是通过大量的随机样本来近似计算问题的解…...

vue 文件扩展名中 esm 、common 、global 以及 mini 、 dev 、prod 、runtime 的含义
vue 文件扩展名中 esm 、common 、global 以及 mini 、 dev 、prod 、runtime 的含义 vue.js 直接用在 script 标签中的完整版本(同时包含编译器 compiler 和运行时 runtime),可以看到源码,适用于开发环境。 这个版本视图可以写在…...

微服务契约测试框架Pact-Python实战
Pact是一个契约测试框架,有多种语言实现,本文以基于pact-python探究契约测试到底是什么?以及如何实现 官网:自述文件 |契约文档 (pact.io) 契约测试步骤 1、为消费者写一个单元测试,让它通过,并生成契约…...

Linux 给用户 赋某个文件夹操作的权限(实现三权分立)
Linux 给用户 赋某个文件夹操作的权限 这里用的ubuntu16.04 一、配置网站管理员 linux文件或目录的权限分为,读、写、可执行三种权限。文件访问的用户类别分为,文件创建者、与文件创建者同组的用户、其他用户三类。 添加用户 useradd -d /var/www/htm…...

【C++入门到精通】C++入门 —— 类和对象(初始化列表、Static成员、友元、内部类、匿名对象)
目录 一、初始化列表 ⭕初始化列表概念 ⭕初始化列表的优点 ⭕使用场景 ⭕explicit关键字 二、Static成员 ⭕Static成员概念 🔴静态数据成员: 🔴静态函数成员: ⭕使用静态成员的优点 ⭕使用静态成员的注意事项 三、友…...

“深入理解Spring Boot:从入门到高级应用“
标题:深入理解Spring Boot:从入门到高级应用 摘要:本文将介绍Spring Boot的基本概念、原理和使用方法,并探讨如何在实际开发中充分发挥Spring Boot的优势。通过详细的示例代码,读者将能够深入理解Spring Boot的各个方…...

Apache Spark 的基本概念和在大数据分析中的应用
Apache Spark是一种快速、通用、可扩展的大数据处理引擎,用于大规模数据处理任务,如批处理、交互式查询、实时流处理、机器学习和图形处理等。它的主要特点包括: 1. 速度:Spark使用In-Memory计算技术,将计算结果存储在…...
Debian LNMP架构的简单配置使用
一、LNMP简介 LinuxNginxMysqlPHP组成的网站架构,常用于中小型网站服务。 二、环境 Debian 6.1.27-1kali1 (2023-05-12) Nginx/1.22.1 10.11.2-MariaDB(mysql) PHP 8.2.7 (Debian 6.1.27包含以上包,直接使用即…...
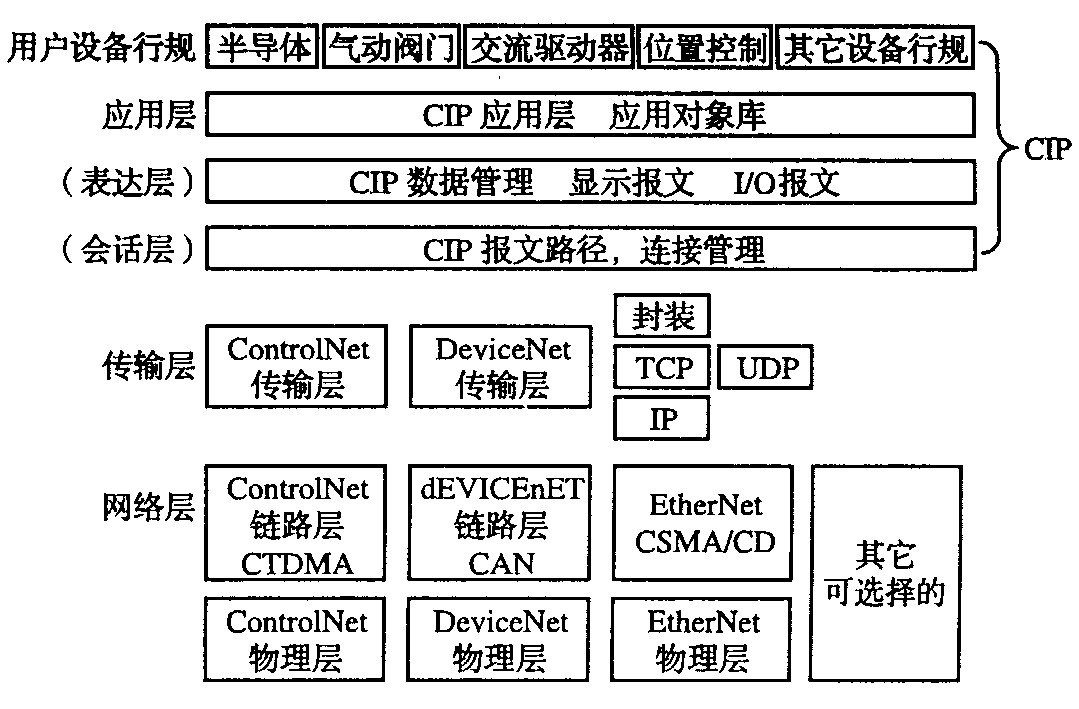
CAN转EtherNet/IP网关can协议破解服务
JM-EIP-CAN 是自主研发的一款 ETHERNET/IP 从站功能的通讯网关。该产品主要功能是将各种 CAN 总线和 ETHERNET/IP 网络连接起来。 本网关连接到 ETHERNET/IP 总线中做为从站使用,连接到 CAN 总线中根据节点号进行读写。 技术参数 ETHERNET/IP 技术参数 网关做为 …...
最适合新手的Java项目/SpringBoot+SSM项目《苍穹外卖》/项目实战、笔记(超详细、新手)[持续更新……]
小知识 软件设计中提到的UI设计中的UI是什么意思? 在软件设计中,UI设计中的UI是User Interface的简称,即用户界面。UI设计是指对软件的人机交互、操作逻辑、界面美观的整体设计。好的UI设计可以让软件变得有个性有品位,同时让操作…...

CloudDriver一款将各种网盘云盘挂在到电脑本地变成本地磁盘的工具 教程
平时我们的电脑可能由于大量的文件资料之类的导致存储空间可能不够,所以我们可以选择将网盘我们的本地磁盘用来存放东西。 CloudDrive 是一款可以将 115、阿里云盘、天翼云盘、沃家云盘、WebDAV 挂载到电脑中,成为本地硬盘的工具,支持 Window…...

行为型模式之中介者模式
中介者模式(Mediator Pattern) 中介者模式是一种行为型设计模式,旨在通过封装一系列对象之间的交互方式,使其能够独立地进行通信。 中介者模式的核心思想是将对象之间的直接通信改为通过一个中介者对象来进行间接通信,…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
